Introducción
En la geometría elemental se tienen varias construcciones realizadas con únicamente regla y compas, esto nos parecerá algo limitante, pero es así como Platón lo plantea para la geometría. Pero son estas restricciones lo que hace interesante las construcciones, cabe aclarar que cuando se menciona regla es para únicamente trazar rectas sin distancia fija, y el compás para trazar circunferencias únicamente. Son estas limitaciones las que hacen que muchas construcciones no se puedan realizar, es en este punto donde hablaremos de ‘Los tres problemas famosos griegos’ los cuales son: La trisección del ángulo, la duplicación del cubo y la cuadratura del círculo.
Este grupo de problemas imposibles enunciados en el siglo V a.C. y hasta la demostración de que la solución es imposible en el siglo XIX, generaron que grandes matemáticos pensaran en su solución, así mismo se motivó al desarrollo de diversas áreas de las matemáticas. Como se mencionó, las restricciones de únicamente regla y compas son las que imposibilitan la solución, pero si se modificaran estas restricciones adecuadamente, estos problemas pueden ser resueltos. Es por ello que se mostrara la imposibilidad de resolver los tres problemas famosos.
Trisección del ángulo
Problema. Lograr trisecar un ángulo arbitrario con regla y compas. Se mostrará la imposibilidad de resolver este problema.
Demostración. Dado un ángulo, no siempre es posible construir solo con una regla y compas un ángulo cuya medida es un tercio del ángulo original.
Tenemos que mostrar lo que significa construir un ángulo a números construibles, ya que un número construible es la longitud de un segmento, no una medida de un ángulo. Recordemos que si tenemos algún ángulo construido sin perdida de generalidad, se asume que este ángulo está en la posición estándar, de modo que su lado inicial este en el eje $x$ positivo.
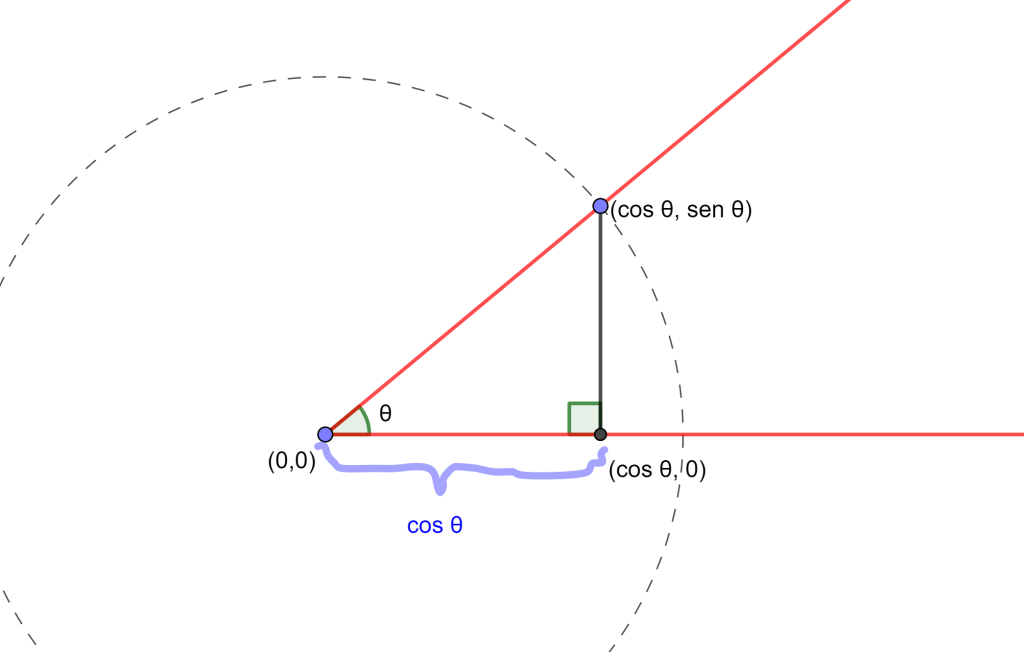
Se puede asignar el vértice del ángulo con el origen de nuestro plano y luego construir un círculo unitario centrado en el origen, donde tendremos un punto de intersección que por trigonometría este punto es ( $cos \theta, sen \theta $ ) y si tomamos la perpendicular de este punto hasta el eje $x$, nos dara un punto ( $cos \theta , 0 $ ) y por lo cual se tiene la distancia $cos \theta$.
Entonces si el angulo theta $\theta$ es construible eso significa que la distancia $cos \theta $ es construible y este proceso es reversible, por lo que podemos construir el ángulo theta $\theta$ si y solo si podemos construir el coseno de distancia de theta $\theta$. Por lo cual se querrá argumentar que el coseno de theta ($cos \theta$) no es un número construible para todos los theta $\theta$.
Tenemos la siguiente identidad trigonométrica
$cos 3\theta = 4 cos^3 \theta – 3 cos \theta.$
Es importante recalcar que queremos $cos 3 \theta$, porque queremos ángulos de trisección. Si tomamos $\theta = 20^o $, entonces ingresándolo en la fórmula se tiene
$cos 3\theta = cos (3)(20^o)=cos 60^o= 1/2.$
Si definimos $\alpha=cos \theta$ entonces se tiene que la igualdad queda
$4\alpha ^3 – 3 \alpha = 1/2.$
Multiplicamos por 2 en ambos lados
$8 \alpha ^3 – 6\alpha = 1$
$8\alpha ^3 – 6 \alpha -1 =0.$
Entonces $\alpha $ es una raíz del polinomio
$8x^3-6x-1.$
Este es un polinomio de grado 3 si es irreducible, eso sucede si y solo si no tiene raíces, porque si es irreducible tiene un factor lineal, y si tiene un factor lineal tiene una raíz por el teorema de las raíces racionales, las únicas raíces racionales posibles de este polinomio son
$\pm 1, \pm 1/2, \pm 1/4, \pm 1/8.$
Ninguno de estos ocho números son raíces de este polinomio, este polinomio por lo cual es irreducible porque no tiene raíces racionales, por lo tanto, este polinomio debe sé el polinomio mínimo para el coseno de $20^o$.
Ahora, ya que este es un polinomio de grado 3, si tomamos el conjunto de los racionales $\alpha$ y vemos su grado sobre $\mathbb{Q}$ tenemos 3.
$[ \mathbb{Q} (\alpha) : \mathbb{Q} ] = 3.$
Pero una propiedad de los números construibles dice que
$[ \mathbb{Q} (\alpha) : \mathbb{Q} ] = 2^n.$
Esto es una potencia de 2, pero 3 no es potencia de 2, $3\neq 2^n.$
Por lo tanto, esto no puede ser una extensión construible, por lo cual el $cos 20^o$ no es un número construible, entonces un ángulo de $20^o$ no se puede construir y un ángulo de $60^o$ no se puede trisecar usando solo regla y compas.
$\square$
Duplicación del cubo
Problema. Se demostrará que la duplicación del cubo es imposible.
Duplicar el cubo nos dice que dada la arista de un cubo, es imposible construir con una regla y compas el borde de un cubo que tiene el doble del volumen del cubo original.
Demostración. Imaginemos el cubo con la longitud de un lado de $S$ y este es un número construible, el volumen de este cubo sería $V=S^3$; Por lo cual si tuviéramos que construir un cubo cuyo volumen sea el doble, entonces el volumen sería $V=2S^3$ este cubo es más grande, y nos preguntaremos cuanto deben medir los lados de este nuevo cubo.
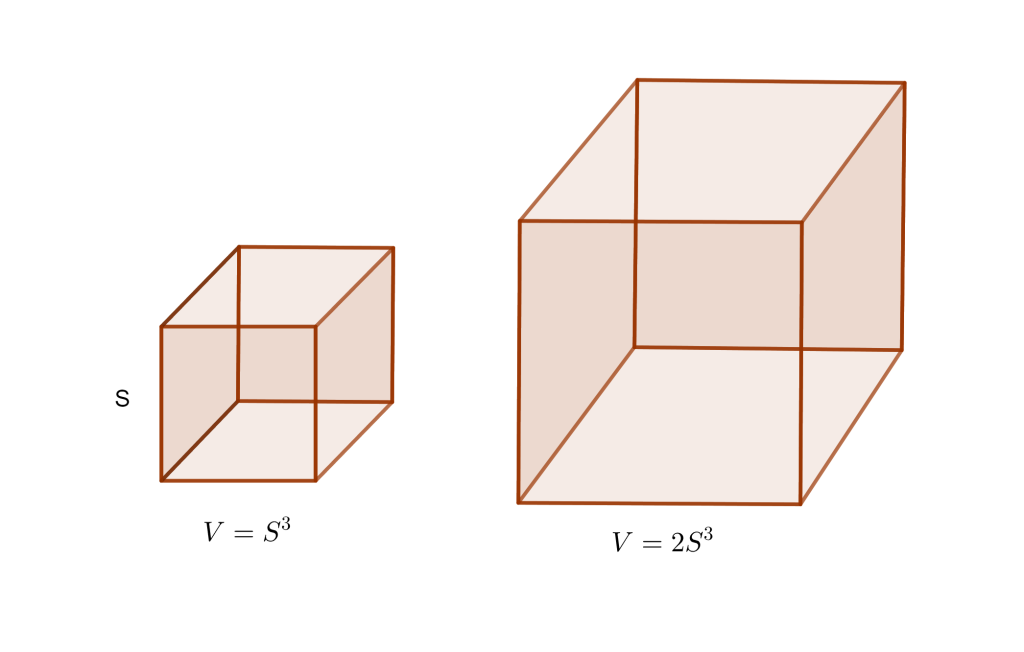
Entonces el cubo duplicado, su volumen debe ser $2S^3$, y sea la longitud de lado $t$, entonces el $V=t^3=2S^3$, despejando $t$ se tiene
$t=\sqrt[3]{2S^3}=\sqrt[3]{2}S.$
Ahora el cuerpo de números construibles es un campo, si podemos construir $S$, entonces podemos dividir por $S$, pero $\sqrt[3]{2}$ no es número construible, ya que
$[ \mathbb{Q} (\sqrt[3]{2}) : \mathbb{Q} ] = 3.$
Pero una propiedad de los números construibles dice que ($\alpha$ es un número construible)
$[ \mathbb{Q} (\alpha) : \mathbb{Q} ] = 2^n.$
Pero $3\neq 2^n$, entonces $\sqrt[3]{2}$ no se puede construir y, por lo tanto, no podemos duplicar el cubo.
$\square$
Cuadratura del círculo
Problema. Por demostrar la imposibilidad de la construcción geométrica clásica de cuadrar el círculo.
Demostración. Dado un círculo de diámetro construible, no siempre es posible construir solo con una regla y compas el borde de un cuadrado que tiene la misma área que el círculo original.
El contraejemplo será que, se tome el círculo unitario, con radio $r=1$ número construible, el área es $A=\pi r^2 = \pi$.
Se debe mostrar que no se puede construir un cuadrado cuya área sea $\pi$ y recordemos que si tenemos un cuadrado con lado $S$ y el área es $A=S^2$. Ahora, si $\pi$ fuera igual a $S^2$ ($\pi = S^2$), esto nos diría que si tomas la raíz cuadrada de ambos lados se tiene $\sqrt{\pi}= S.$
Entonces se requiere construir un lado de longitud $\sqrt{\pi}$.
Pero si $\sqrt{\pi}$ fuera construible, entonces si elevamos al cuadrado $\sqrt{\pi}^2 = \pi$ y el campo de números construibles es un campo, por lo cual $\sqrt{\pi}^2$ también es construible, pero $\pi$ es un número trascendental y ninguna extensión algebraica de $\mathbb{Q}$ contiene $\pi$. El campo de números construibles es una extensión algebraica infinita de los números racionales y, por lo tanto, no contiene números trascendentales, y de ahí se tiene la contradicción $pi$ no es un número construible.
Por lo tanto, es imposible construir un cuadrado para cada círculo.
$\square$
Más adelante…
Se verá el Teorema de Stewart.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Construcciones con regla o compas
- Siguiente entrada del curso: Teorema de Stewart