Introducción

Otro tema interesante son los Teoremas de Carnot, los cuales nos permiten resolver otros problemas.

Teoremas de Carnot

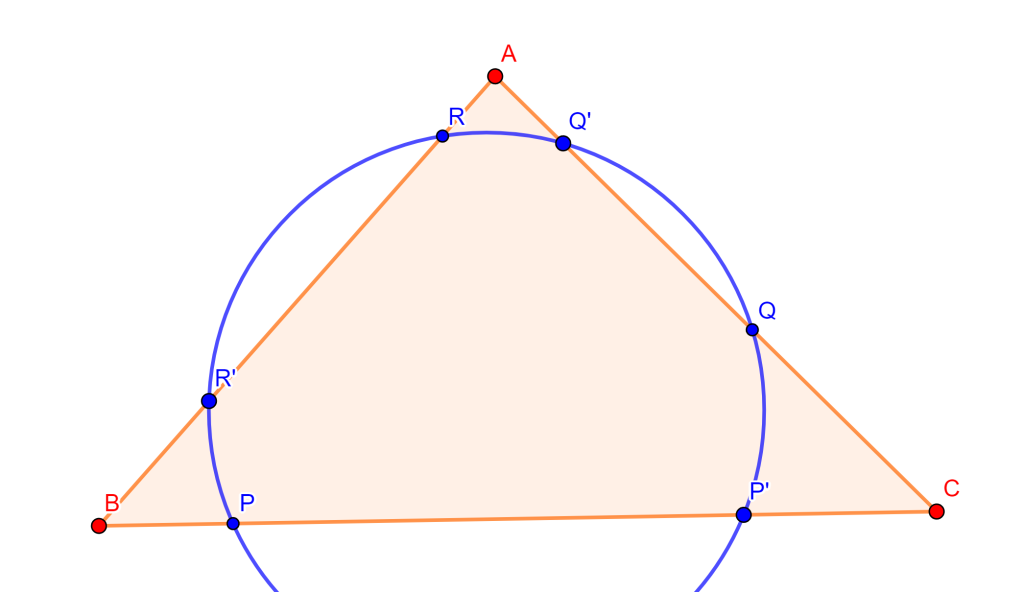
Teorema. Sea, $ABC$ un triángulo y una circunferencia que interseca en los lados $BC$, $CA$, $AB$ en los puntos $P$, $P’$, $Q$, $Q’$, $R$, $R’$ respectivamente, entonces

$\frac{AR}{RB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR’}{R’B} \cdot \frac{BP’}{P’C} \cdot \frac{CQ’}{Q’A} = 1.$

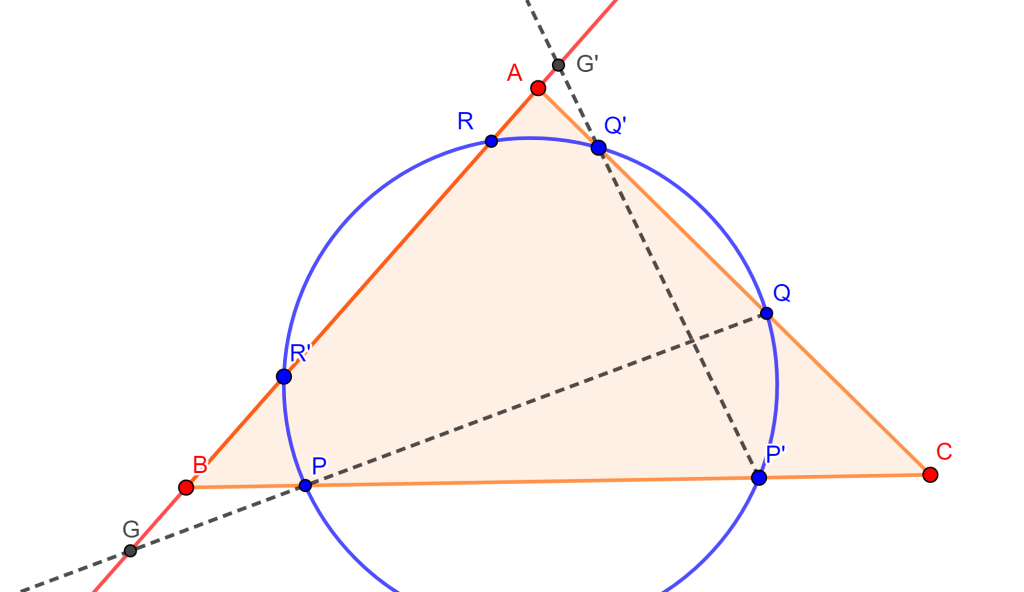
Demostración. Tracemos las rectas $PQ$ y $P’Q’$, las cuales intersecan a $AB$ en $G$ y $G’$ respectivamente. Por Menelao al triángulo $ABC$ con transversales $QG$ y $Q’G’$, se tiene

$\frac{AG}{GB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} = -1$ . . . (1)

y

$\frac{AG’}{G’B} \cdot \frac{BP’}{P’C} \cdot \frac{CQ’}{Q’A} = -1$ . . . (2)

Como $AB$ es una transversal que corta los lados del cuadrángulo inscrito $PQP’Q’$ y la circunferencia en puntos de involución, se tiene

$\{ABR’G’\}=\{BARG\}=\{ABGR\}.$

Entonces

$\frac{AR}{RB} \cdot \frac{AR’}{R’B} = \frac{AG}{GB} \cdot \frac{AG’}{G’B}.$

Se realizará la siguiente multiplicación de la ecuación (1) y (2)

$\frac{AG}{GB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AG’}{G’B} \cdot \frac{BP’}{P’C} \cdot \frac{CQ’}{Q’A} = (-1)(-1)$

$\frac{AR}{RB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR’}{R’B} \cdot \frac{BP’}{P’C} \cdot \frac{CQ’}{Q’A} = 1.$

$\square$

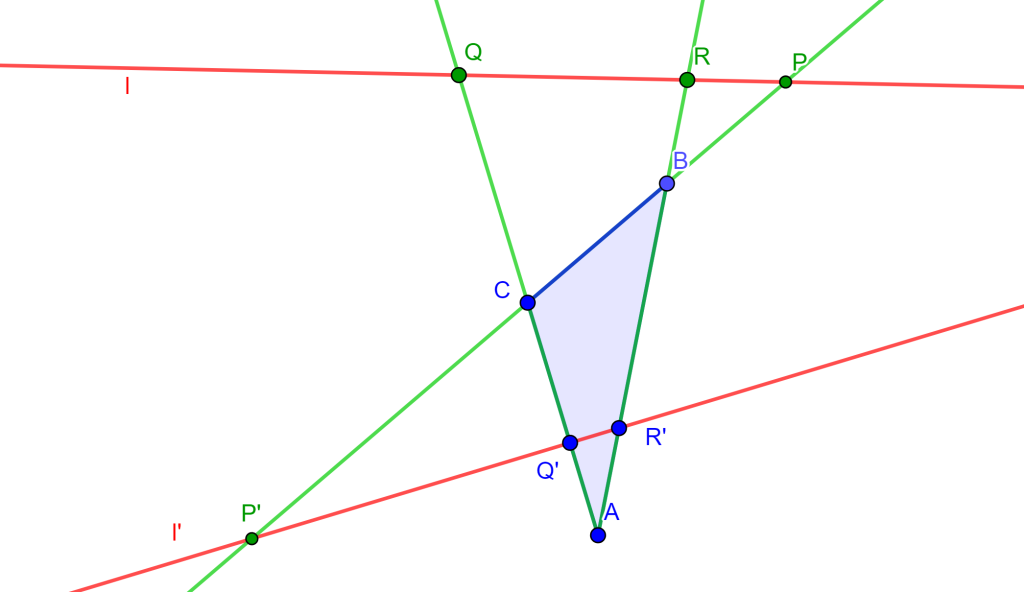
Teorema. (Carnot para Rectas) Sea el triángulo $ABC$ y dos rectas $l$ y $l’$ que intersecan a los lados $BC$, $CA$ y $AB$ la primera en los puntos $P$, $Q$ y $R$ y la segunda a los puntos $P’$, $Q’$ y $R’$, entonces

$\frac{AR}{RB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR’}{R’B} \cdot \frac{BP’}{P’C} \cdot \frac{CQ’}{Q’A} = 1.$

Demostración Por el Teorema de Menelao con las rectas $l$ y $l’$, se tiene

$\frac{AR}{RB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} = -1$ y  $\frac{AR’}{R’B} \cdot \frac{BP’}{P’C} \cdot \frac{CQ’}{Q’A} = -1.$

Entonces multiplicándolos

$\frac{AR}{RB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR’}{R’B} \cdot \frac{BP’}{P’C} \cdot \frac{CQ’}{Q’A} = 1.$

$\square$

Teorema. (Carnot para cónicas) Sea el triángulo $\triangle ABC$ y sea una cónica que interseca los lados $BC$, $CA$ y  $AB$ en los puntos $P$, $P’$, $Q$, $Q’$, $R$, $R’$ respectivamente, entonces

$\frac{AR}{RB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR’}{R’B} \cdot \frac{BP’}{P’C} \cdot \frac{CQ’}{Q’A} = 1.$

Más adelante…

Se dejarán una serie de ejercicios para poner en práctica lo visto en esta unidad.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Teorema de Miquel
• Siguiente entrada del curso: Ejercicios Unidad 5