Introducción
Se discutirán a través de esta unidad teoremas selectos debido a su importancia en la solución de otros problemas, en esta nota será el Teorema de Stewart.
Teorema de Stewart
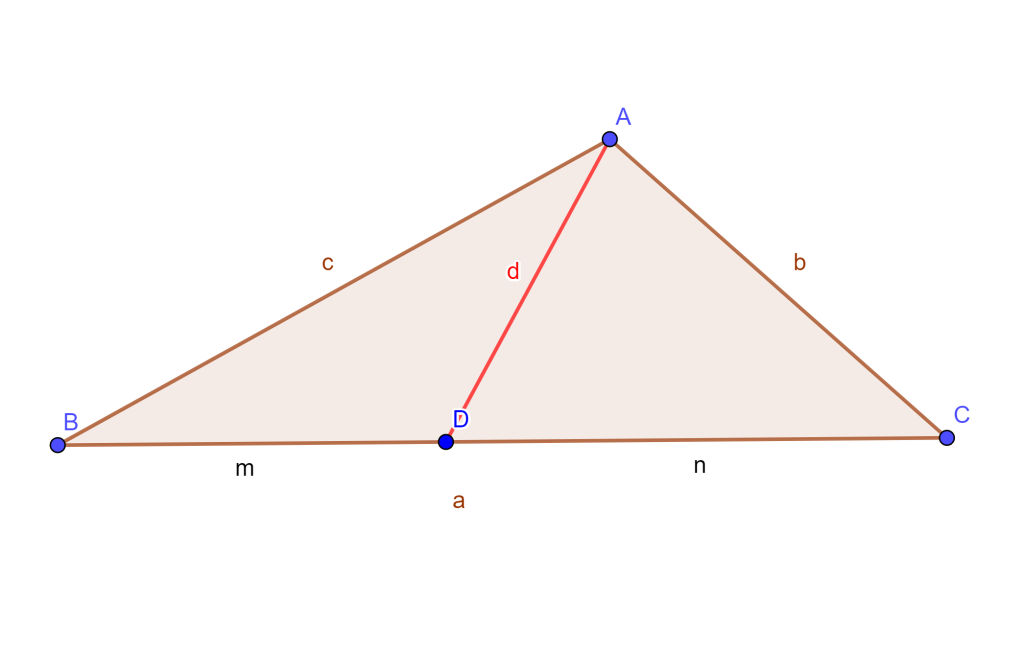
Teorema. Sea el triángulo $ABC$ con lados $BC,CA,AB$ los cuales sus longitudes son $a,b,c$ respectivamente, y sea un punto $D$ cualquiera en $BC$ donde $BC=m$ y $DC=n$, además si la longitud de $AD=d$, entonces
$ad^2=mb^2+nc^2-amn.$
Demostración Aplicando la Ley de cosenos a los triángulos $\triangle ABD$ en el ángulo $\angle ADB $ y el $\triangle ADC$ en el ángulo $\angle ADB$, se tiene
$c^2=d^2+m^2-2dm cos \angle ADB$
y
$b^2=d^2+n^2+2dn cos \angle ADB.$
Si multiplicamos ambas ecuaciones por $n$ y $m$ respectivamente tenemos:
$nc^2=nd^2+nm^2-2dnm cos \angle ADB$
y
$mb^2=md^2+mn^2+2dnm cos \angle ADB.$
Sumando ambas ecuaciones se tiene:
$nc^2+mb^2=nd^2+md^2+nm^2+mn^2.$
Ahora como $m+n=a$, se tiene:
$nc^2+mb^2=(n+m)d^2+(n+m)mn$
$nc^2+mb^2=ad^2+amn.$
Por lo tanto, concluimos que:
$ad^2=mb^2+nc^2-amn.$
$\square$
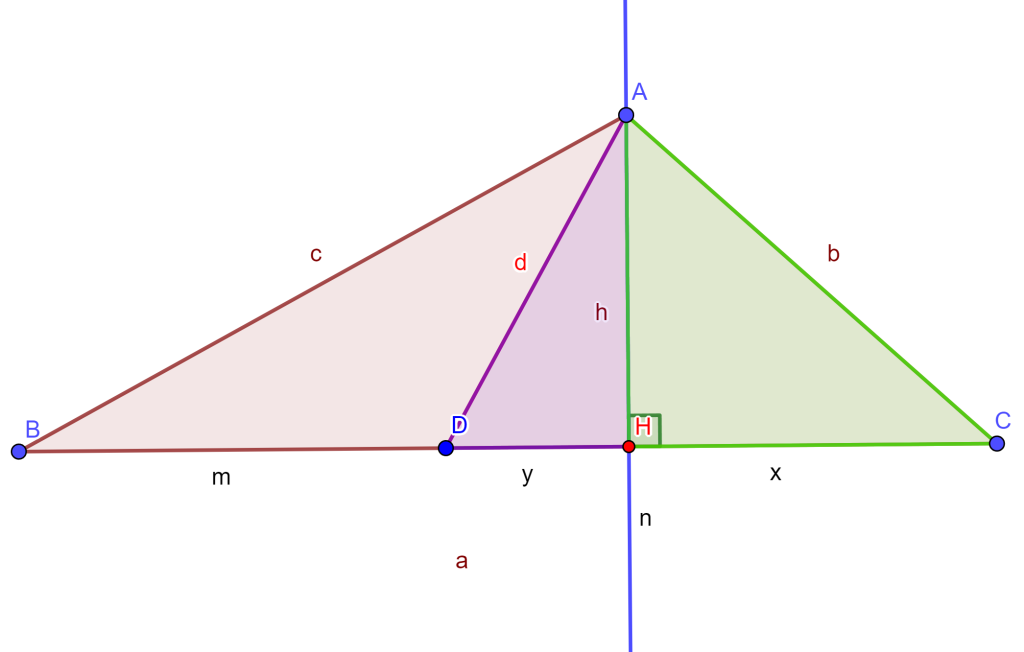
Demostración. (Por Pitágoras) Se tiene la altura de $A$ a $BC$ que corta en el punto $H$, donde $AH=h$, $CH=x$, $HD=y$.
Aplicando el Teorema de Pitágoras al triángulo $\triangle AHC$, $\triangle AHD$ y al $\triangle AHB$ se tiene lo siguiente respectivamente:
$b^2=x^2+h^2$ , $d^2=h^2+y^2$ y $c^2=h^2+(m+y)^2.$
Además se tiene que $y+x=n$ entonces $x=n-y$. Si lo sustituimos en $b^2=h^2+x^2$ se tiene $b^2=h^2+(n-y)^2$ y lo multiplicamos por $m$:
$mb^2=mh^2+m(n-y)^2.$
De igual forma multipliquemos $c^2=h^2+(m+y)^2$ por $n$:
$nc^2=nh^2+n(m+y)^2.$
Entonces sumando $md^2 + nc^2$ se tiene:
$mb^2+nc^2=mh^2+m(n-y)^2+nh^2+n(m+y)^2$
$mb^2+nc^2=(m+n)h^2+m(n^2-2ny+y^2)+n(m^2+2my+y^2)$
$mb^2+nc^2=(m+n)h^2 + mn^2-2mny+my^2+nm^2+2mny+ny^2$
$mb^2+nc^2=(m+n)h^2+mn^2+nm^2+my^2+ny^2$
$mb^2+nc^2=mn(n+m)+(m+n)(y^2+h^2)$
$mb^2+nc^2=(m+n)[mn+y^2+h^2].$
Sustituyendo $d^2=h^2+y^2$ y $m+n=a$ en la ecuación resultante:
$mb^2+nc^2=a[mn+d^2].$
Por lo tanto,
$ad^2=mb^2+nc^2-amn.$
$\square$
Conclusión
Es gracias a este Teorema que se puede encontrar la longitud de la recta $AB$ cuando $D$ es un punto cualquiera en la recta $BC$ y se tiene la razón en la cual $D$ divide a $BC$, ya que se conocen las longitudes y signos de $BD$ y $DC$ en este caso.
De igual forma, las longitudes de las medianas, las simedianas y las bisectrices de los ángulos de un triángulo, se pueden encontrar usando el Teorema de Stewart.
Con el uso del teorema de Stewart se puede resolver el siguiente Teorema.
Teorema. Si las bisectrices de dos ángulos interiores de un triángulo son iguales, el triángulo es isósceles.
Más adelante…
Se abordará el Teorema de Miquel.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Los tres problemas famosos
- Siguiente entrada del curso: Teorema de Miquel