Introducción
Tres teoremas importantes en la razón cruzada son el Teorema de Pascal, Brianchon y Pappus. Con estos se muestran propiedades de colinealidad y concurrencia.
Teorema de Pascal
Teorema. Sea un hexágono inscrito en una circunferencia, los puntos de intersección de sus lados opuestos son colineales.
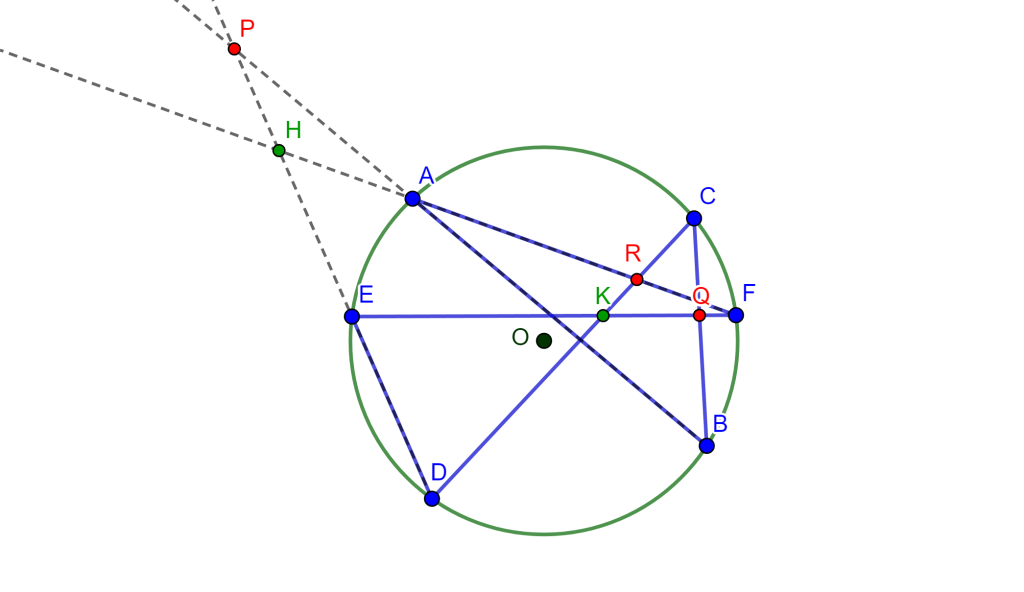
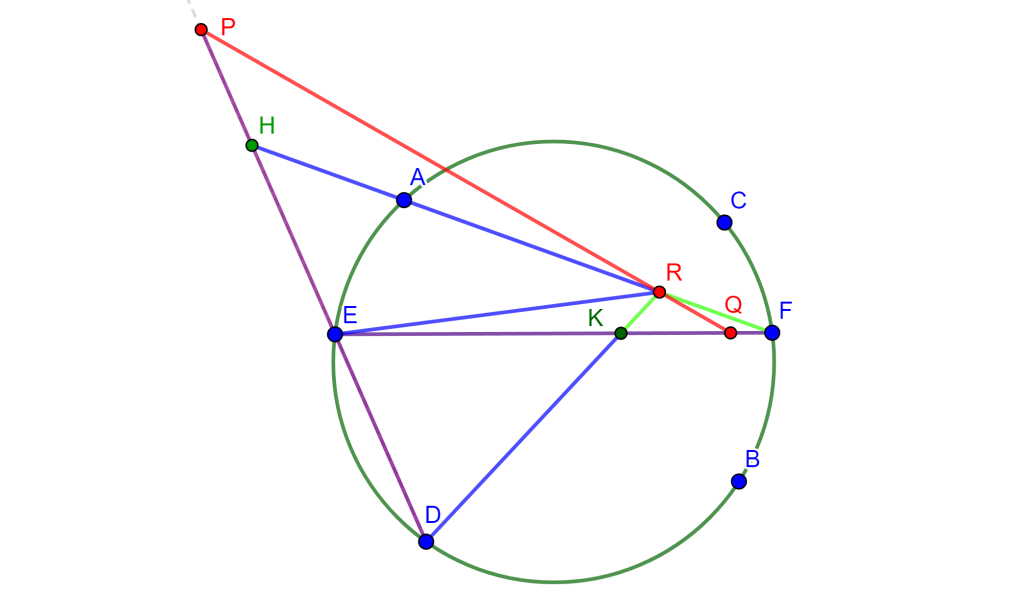
Demostración. Sea el hexágono inscrito $ABCDEF$ en la circunferencia $O$, donde sus lados opuestos $AB,DE$, $BC,EF$ y $CD,FA$ se intersecan en los puntos $P,Q$ y $R$ son colineales. Ahora $FA$ interseca a $DE$ en $H$ y $EF$ interseca a $CD$ en $K$.
Por propiedades de razón cruzada en la circunferencia se tiene $A\{EDBF\}=C\{EDBF\}$ y por lo cual $\{EDPH\}=\{EKQF\}$, como se observa en la siguiente imagen.
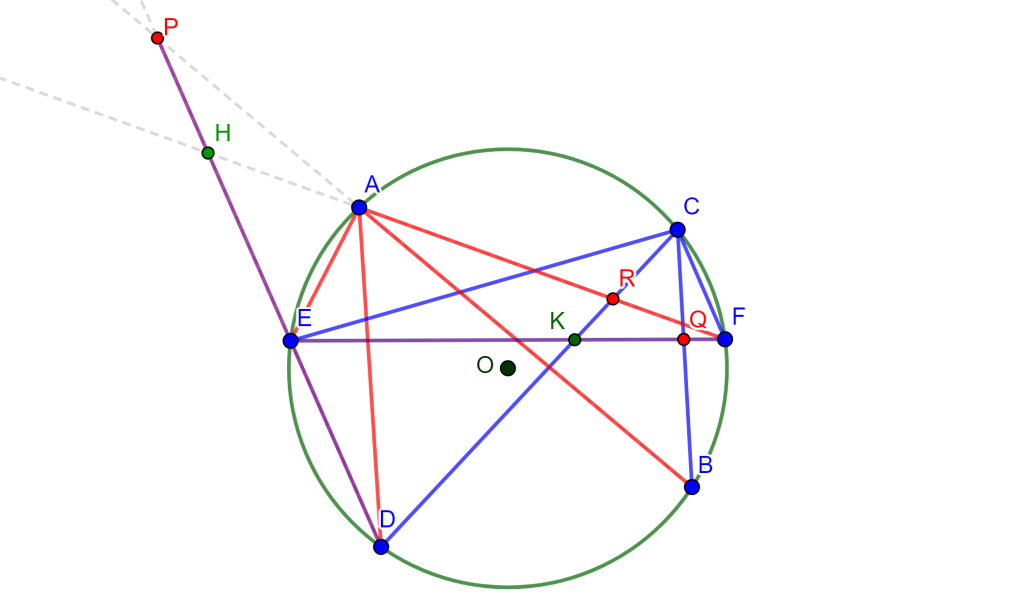
Así mismo se tiene que al unir $R$ con estos puntos se cumple la propiedad $R\{EDPH\}=R\{EKQF\}$. Donde $RE$ coincide con $RE$, $RD$ coincide con $RK$ y $RH$ coincide con $RF$, por ende estos dos haces coinciden en la primera, segunda y cuarta recta, y al tener 3 rectas y una constante distinta de -1, es posible construir una única cuarta recta tal que la razón cruzada sea la constante elegida por ello $RP$ coincide con $RQ$. Y, por lo tanto, $PQR$ son colineales y a esta es la línea de Pascal del hexágono.
$\square$
Teorema de Brianchon
Este es un teorema dual al de Pascal, el cual es aplicable a hexágonos circunscritos a cualquier sección cónica. En nuestro caso se mostrará para una circunferencia.
Teorema. Sea un hexágono circunscrito a una circunferencia, entonces las líneas que unen sus vértices opuestos son concurrentes.
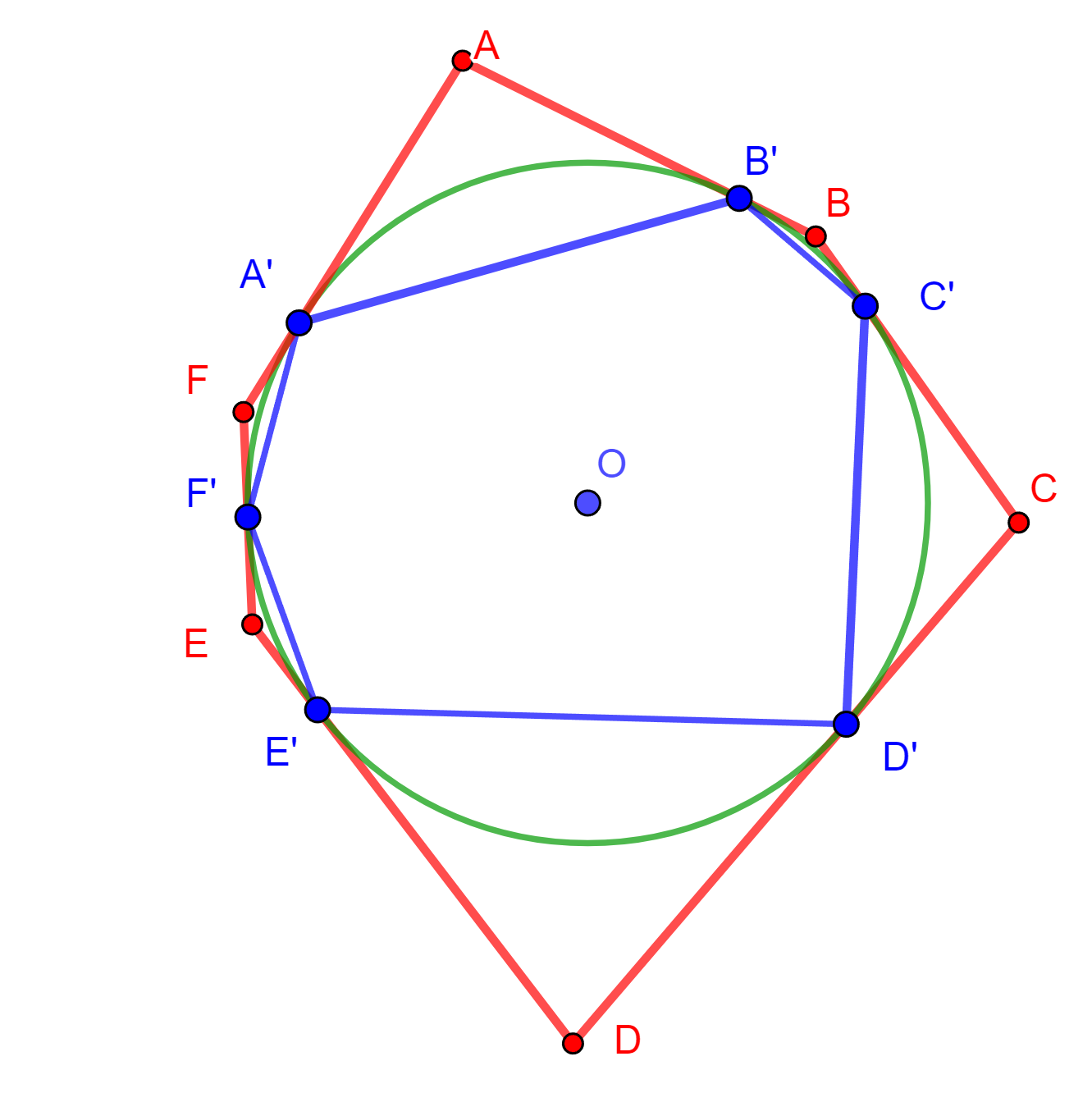
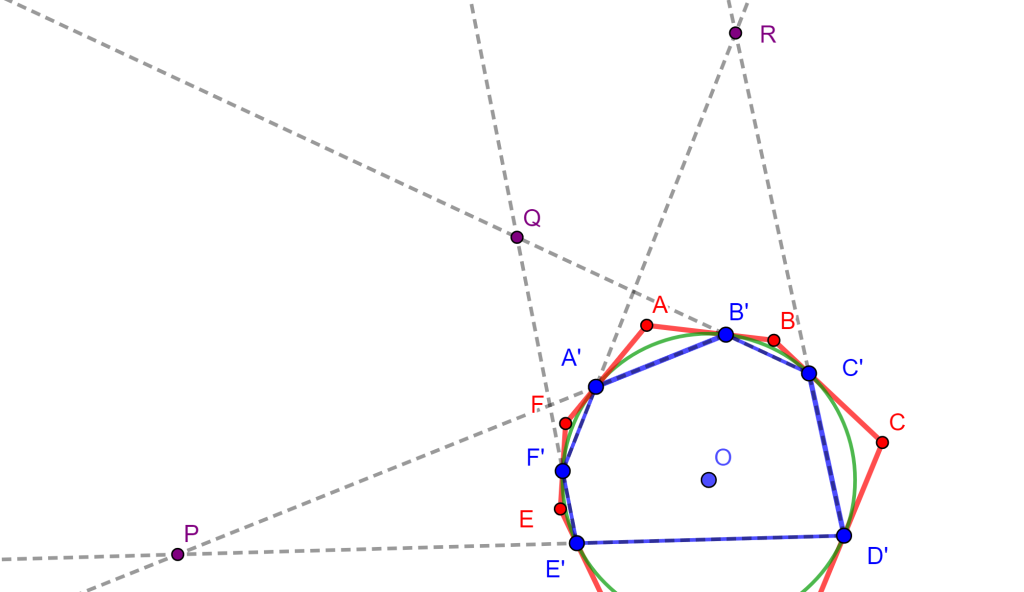
Demostración. Sea el hexágono $ABCDEF$ circunscrito a la circunferencia $O$, ahora los puntos de tangencia de los lados del hexágono $ABCDEF$ son los vértices del hexágono $A’B’C’D’E’F’$.
Si observamos los lados opuestos del hexágono $A’B’C’D’E’F’$ estos se intersecan de la siguiente forma:
- $A’B’$ y $D’E’$ en $P$
- $B’C’$ y $E’F’$ en $Q$
- $C’D’$ y $F’A’$ en $R$
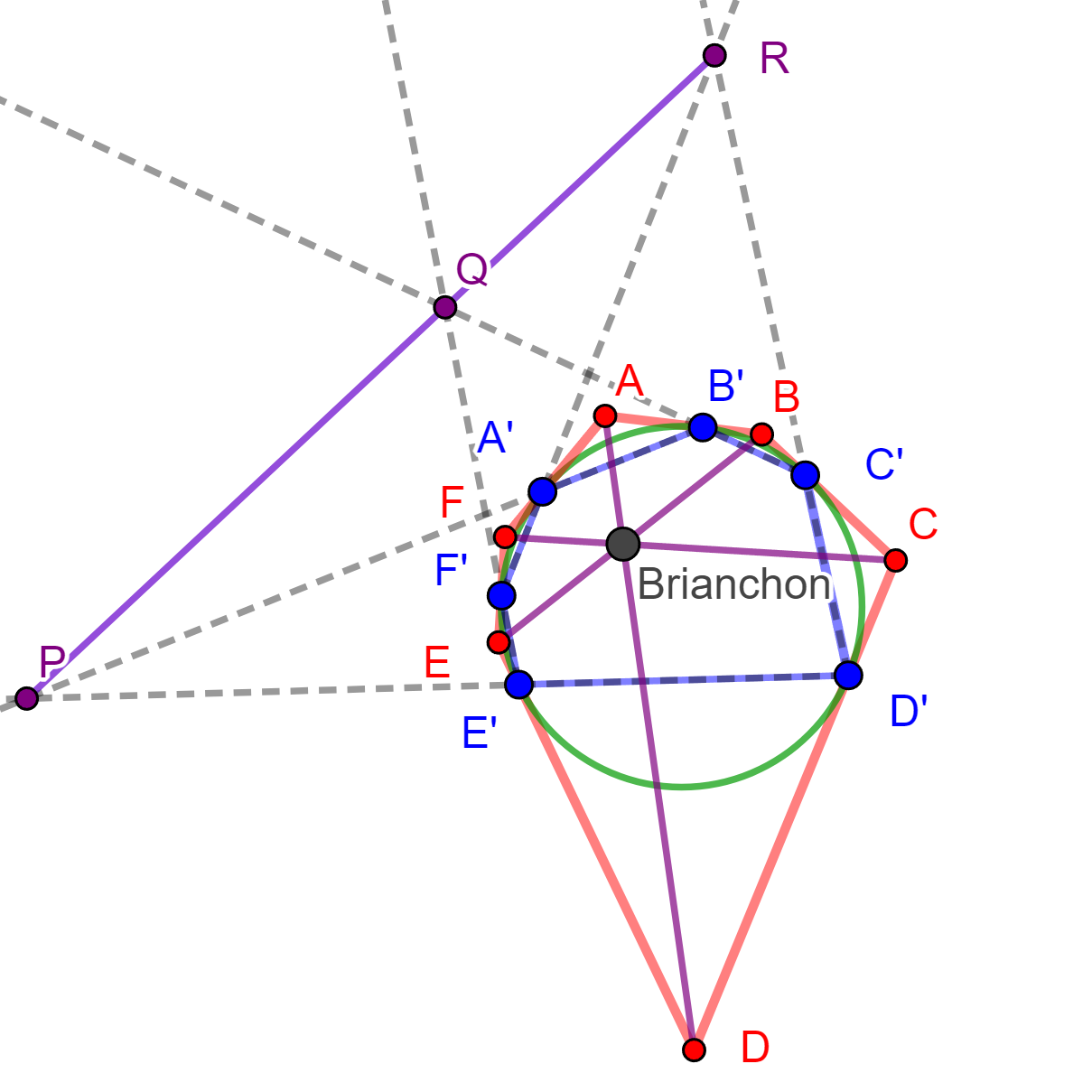
Por propiedad de los Polos y Polares, las polares de $A$ y $D$ pasan por $P$ y la polar de $P$ es $AD$. De igual forma, la polar de $Q$ es $BE$ y la polar de $R$ es $CF$, y por el Teorema de Pascal el hexágono inscrito $A’B’C’D’E’F’$ los puntos de intersección de sus lados opuestos $P$, $Q$ y $R$ son colineales, y por lo cual sus polares $AD$, $BE$ y $CF$ son concurrentes y a este es el punto de Brianchon.
$\square$
Teorema de Pappus
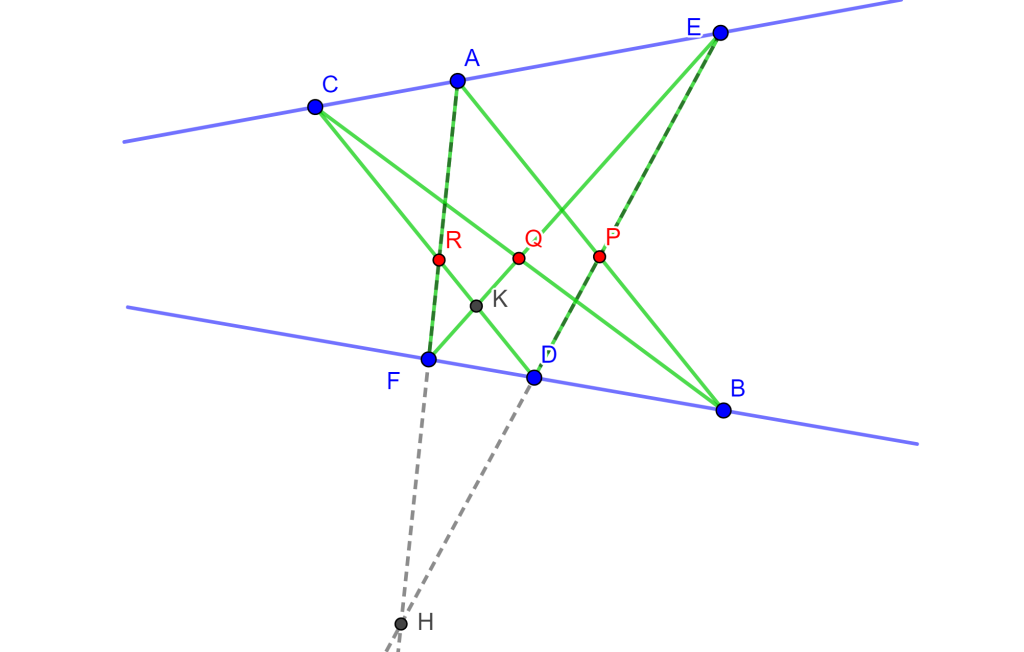
Teorema. Si los vértices de un hexágono están alternativamente en dos líneas rectas, entonces la intersección de los pares de lados opuestos genera puntos los cuales son colineales.
Demostración. Este es un caso especial del Teorema de Pascal para un hexágono inscrito en una sección cónica. Sea el hexágono $ABCDEF$, donde la intersección de los lados opuestos son:
- $AB$ y $DE$ en $P$
- $BC$ y $EF$ en $Q$
- $CD$ y $FA$ en $R$
Se tiene que $AF$ interseca a $ED$ en $H$, y $EF$ interseca a $CD$ en $K$.
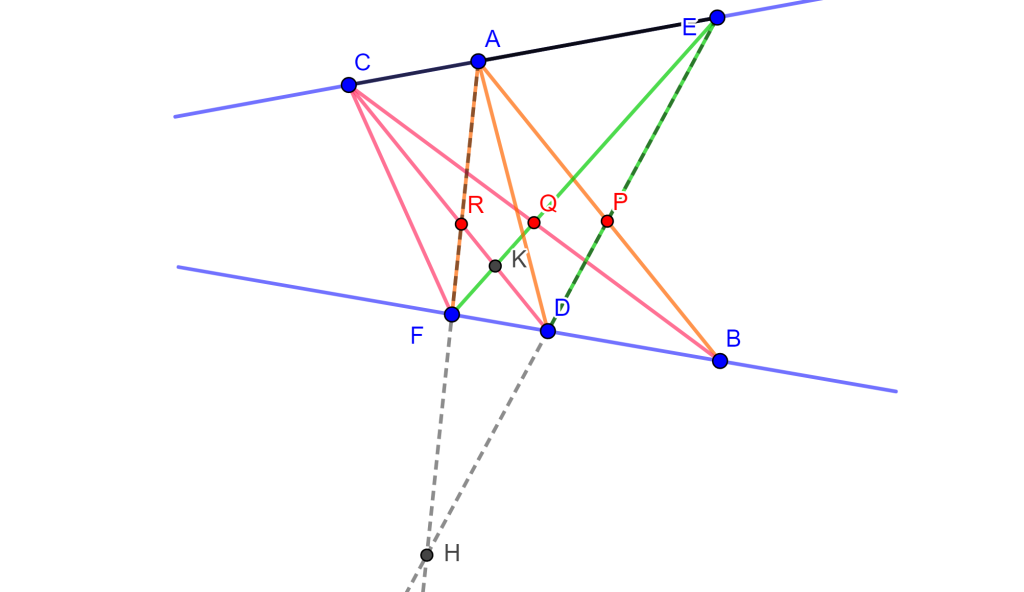
Por lo cual $A\{EBDF\}$ es igual a $C\{EBDF\}$, entonces $\{EPDH\}=\{EQKF\}$.
Uniendo $RQ$ los cuatro puntos de las líneas $ED$ y $EF$, se tiene que $R\{EPDH\}=R\{EQKF\}$.
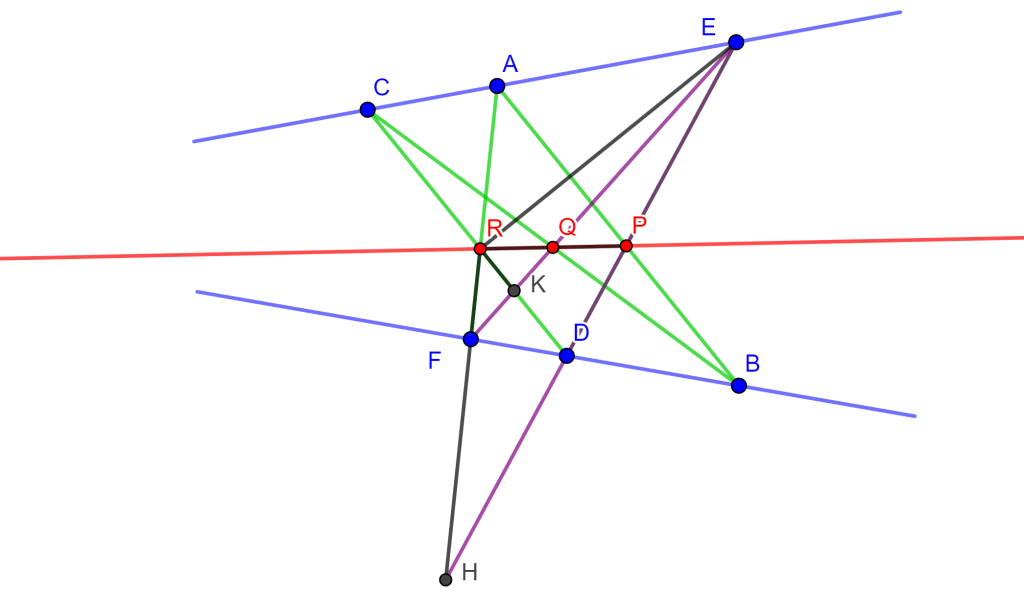
Ahora como $RE$ coincide con $RE$, $RD$ coincide con $RK$ y $RH$ coincide con $RF$, entonces $RP$ y $RQ$ coinciden, por lo tanto, $P$, $Q$ y $R$ son colineales.
$\square$
Más adelante…
Otro tema interesante por abordar es la involución tanto en Hileras de puntos como Haces de líneas.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Puntos autocorrespondientes y regla geométrica de la falsa posición
- Siguiente entrada del curso: Hileras de puntos en involución