Introducción

En geometría euclidiana existen los Teoremas de Miquel, dados por el matemático Auguste Miquel, los cuales son relacionados con circunferencias concurrentes.

Teoremas de Miquel

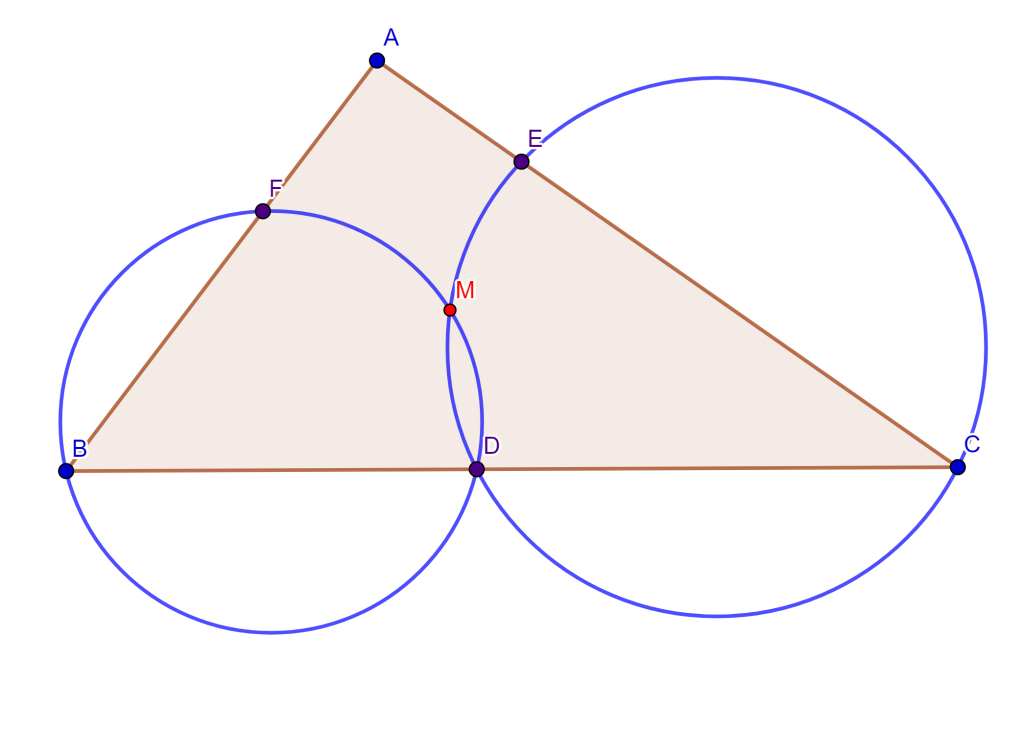
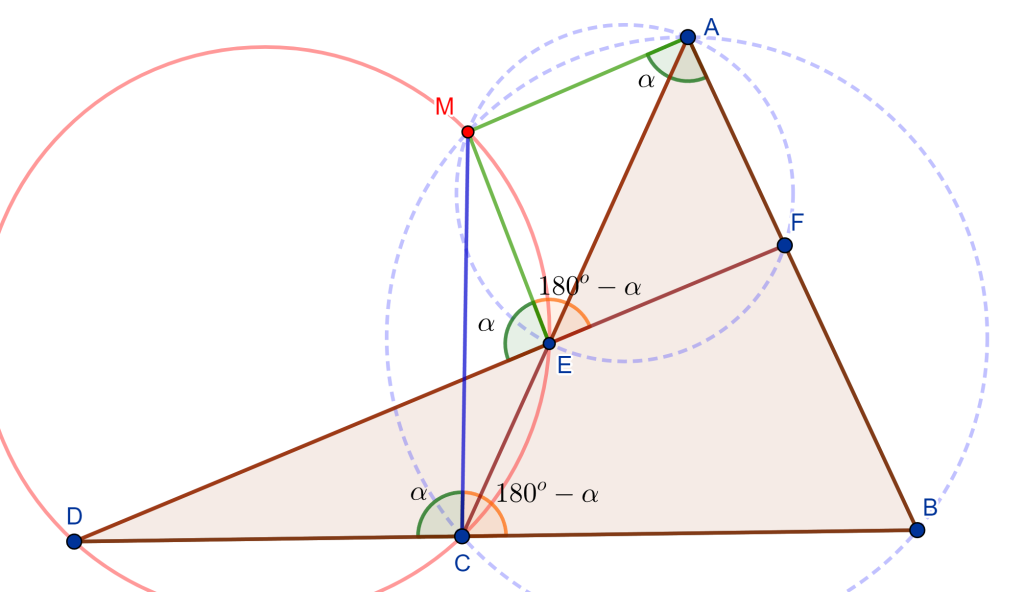
Teorema. Dado el triángulo $\triangle ABC$ y $DEF$ tres puntos cualesquiera en los lados $BC$, $CA$ y $AB$ respectivamente, entonces los circuncirculos de $AEF$, $BFD$ y $CDE$ se intersecan en un punto en común, este es el punto de Miquel.

Demostración. Sea el triángulo $\triangle ABC$ y sean los tres puntos $DEF$ en los lados de $BC$, $CA$ y $AB$ respectivamente, entonces los circuncirculos $CDE$ y $BFD$ se intersecan en un punto $M$. Solo falta demostrar que el cuadrilátero $AFOE$ es cíclico, ya que probaría que la circunferencia $AFE$ pasa por el punto $M$.

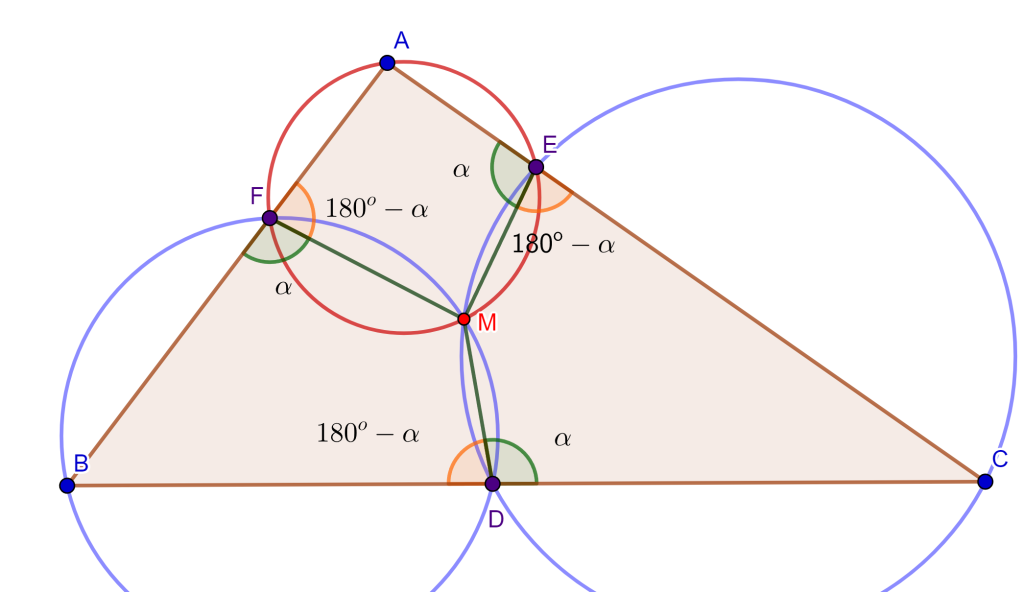
Tracemos $FM$, $ME$ y $MD$, de esta forma se tienen los tres cuadriláteros $FMDB$, $MECD$ y $FAEM$. Tenemos el ángulo $\angle AEM = \alpha $ donde el ángulo $\angle CEM = 180^o – \alpha$, como el cuadrilátero $MECD$ es cíclico entonces el ángulo $\angle MDC = \alpha $, por lo cual el ángulo $\angle MDB = 180 ^o – \alpha$.
Ahora, como el ángulo $\angle MDB = 180^o – \alpha$ y el cuadrilátero $FMDB$ es cíclico, entonces el ángulo $\angle BFM = \alpha$, por lo cual el ángulo $\angle MFA = 180 ^o – \alpha$.

Si observamos el cuadrilátero $FAEM$ sus dos ángulos opuestos $\angle MFA$ y $\angle AEM$ suman $180^o$, por lo cual el cuadrilátero $FAEM$ es cíclico. Por lo tanto, el circuncirculo de $FAE$ pasa por el punto $M$ y los tres circuncirculos se intersecan en el punto $M$ ($M$ es el punto de Miquel).

$\square$

El punto $M$ es el punto de Miquel con respecto al triángulo $\triangle ABC$
El triángulo $DEF$ cuando $D$, $E$ y $F$ no son colineales, es llamado un triángulo de Miquel $M$.
Los tres circuncirculos de $AEF$, $BFD$ y $CDE$ son llamadas las circunferencias de Miquel de los puntos $D$, $E$ y $F$.

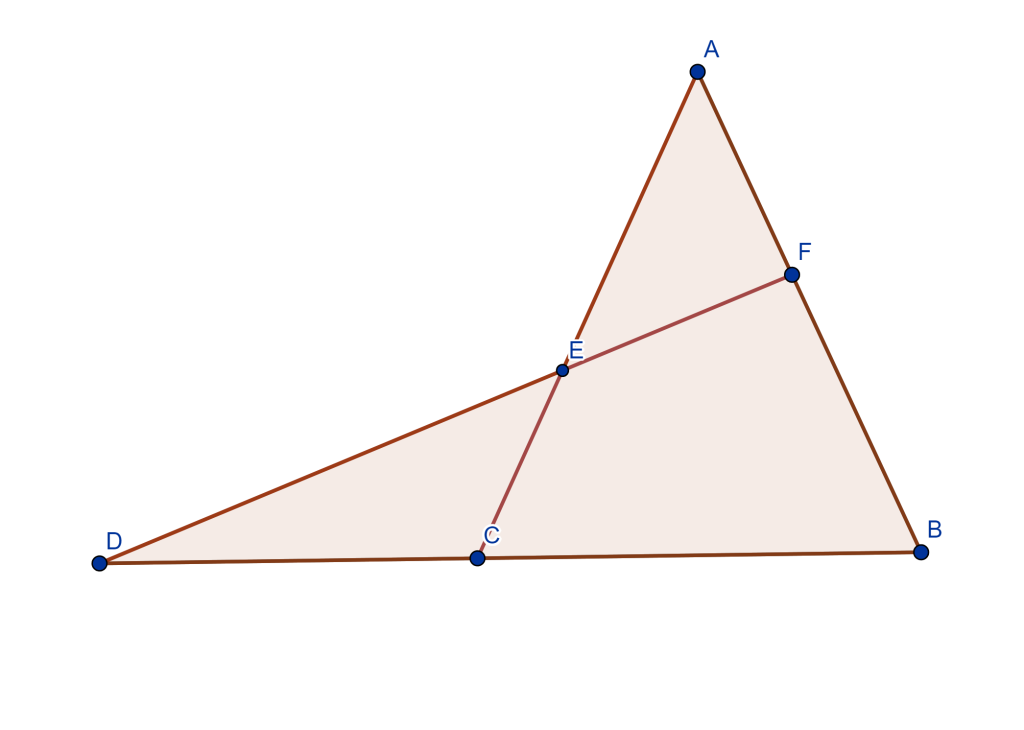
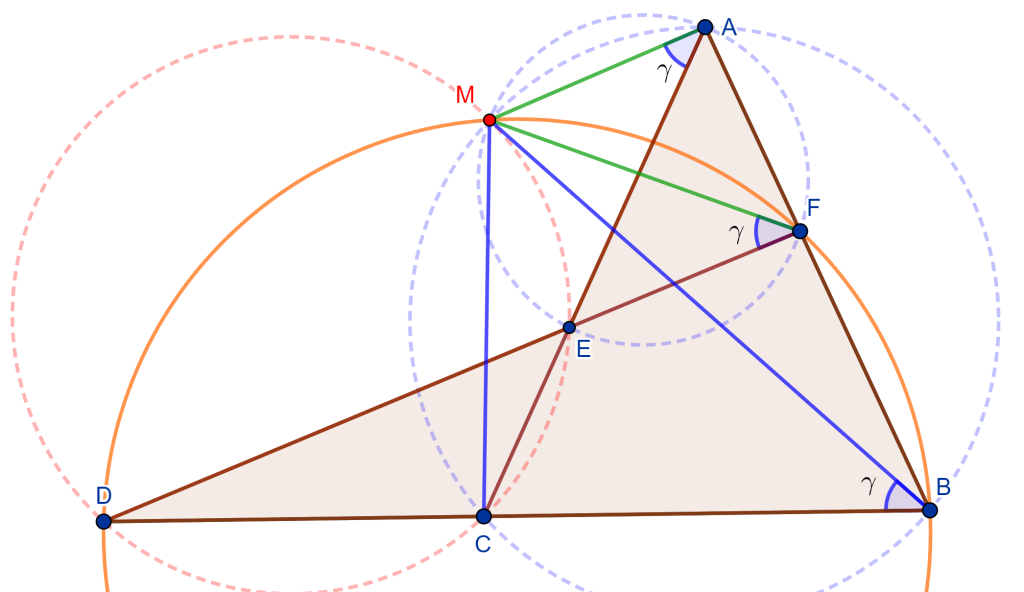
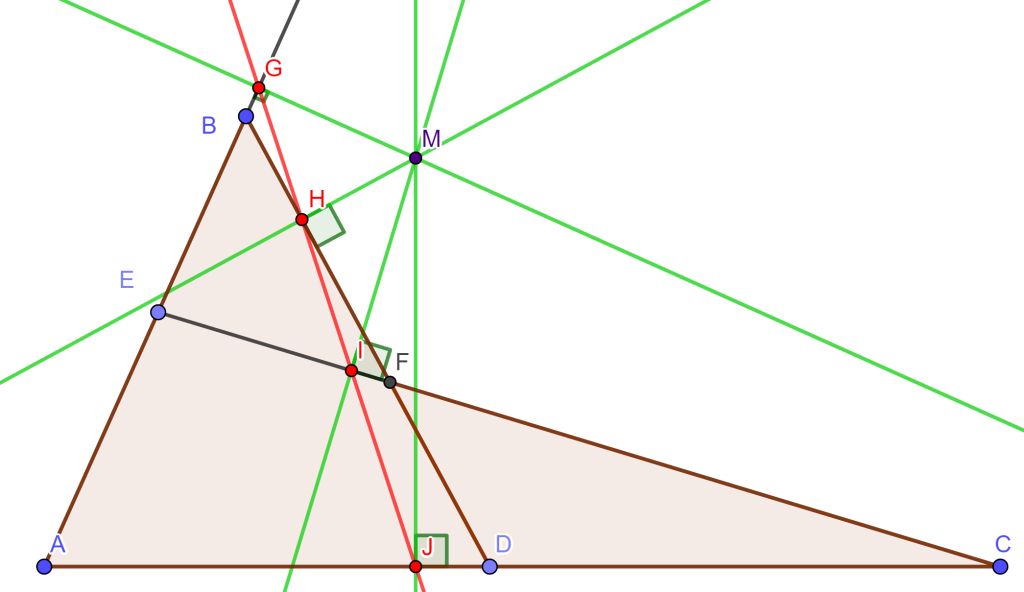
Teorema. (Cuadrilátero Completo) Sea $ABCDEF$ un cuadrilátero completo, entonces las circunferencias circunscritas de los cuatro triángulos $EAD$, $EBC$, $FAB$ y $FDC$ tienen un punto en común, $M$ llamado punto de Miquel.

Demostración.

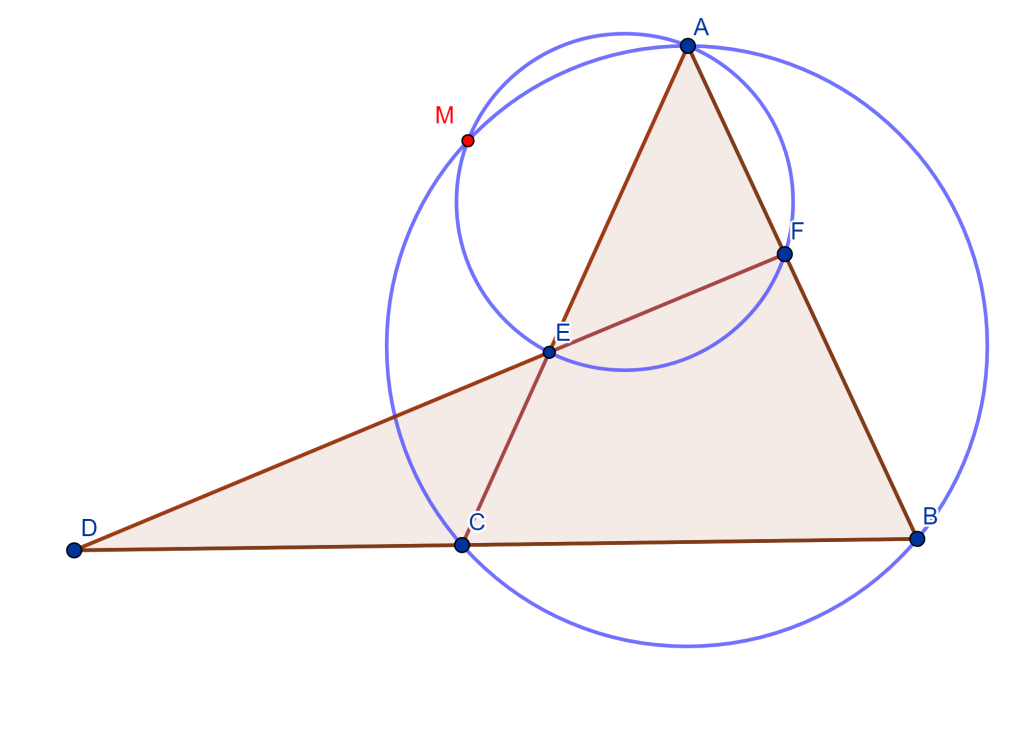
De los triángulos $AEF$ y $ACB$ trazamos sus circunferencias circunscritas que se cortan en un punto $M$.

Mostremos que el cuadrilátero $MECD$ es cíclico, ya que mostraría que su circunferencia circunscrita pasa por $M$.
Observemos el ángulo $\angle DCM = \alpha$ y $\angle MCB = 180 ^o – \alpha$, ahora tenemos el cuadrilátero cíclico $MCBA$ entonces el ángulo $\angle MAB = \alpha$, el cuadrilátero cíclico $MAFE$ tiene el ángulo $\angle MAF = \alpha$ entonces $\angle MEF = 180 ^o – \alpha$.

Como $\angle MEF = 180^o – \alpha$ entonces $\angle MED = \alpha$, ahora veamos el cuadrilátero $MECD$ tiene los ángulos $\angle MED = \alpha $ y $\angle DCM = \alpha$, lo que nos lleva a que el cuadrilátero $MECD$ es cíclico y su circunferencia circunscrita pasa por $M$.

Falta por demostrar que el cuadrilátero $MDBF$ es cíclico.
Sea el ángulo $\angle MFE = \gamma$, el cuadrilátero $MAFE$ es cíclico, entonces tiene un ángulo $\angle MAE = \gamma = \angle MFE$. Observemos ahora el cuadrilátero $MCBA$ cíclico, con su ángulo $\angle MAC = \gamma$ y como es cíclico entonces el ángulo $\angle MBC = \gamma$.
Notemos que el cuadrilátero $MDBF$ tiene los ángulos $\angle MFD = \gamma$ y $\angle MBD = \gamma$, por lo cual el cuadrilátero $MDBF$ es cíclico, entonces su circunferencia circunscrita pasa por $M$.

Por lo tanto, las circunferencias circunscritas de los cuatro triángulos $EAD$, $EBC$, $FAB$ y $FDC$ tienen un punto en común $M$ llamado punto de Miquel $M$.

$\square$

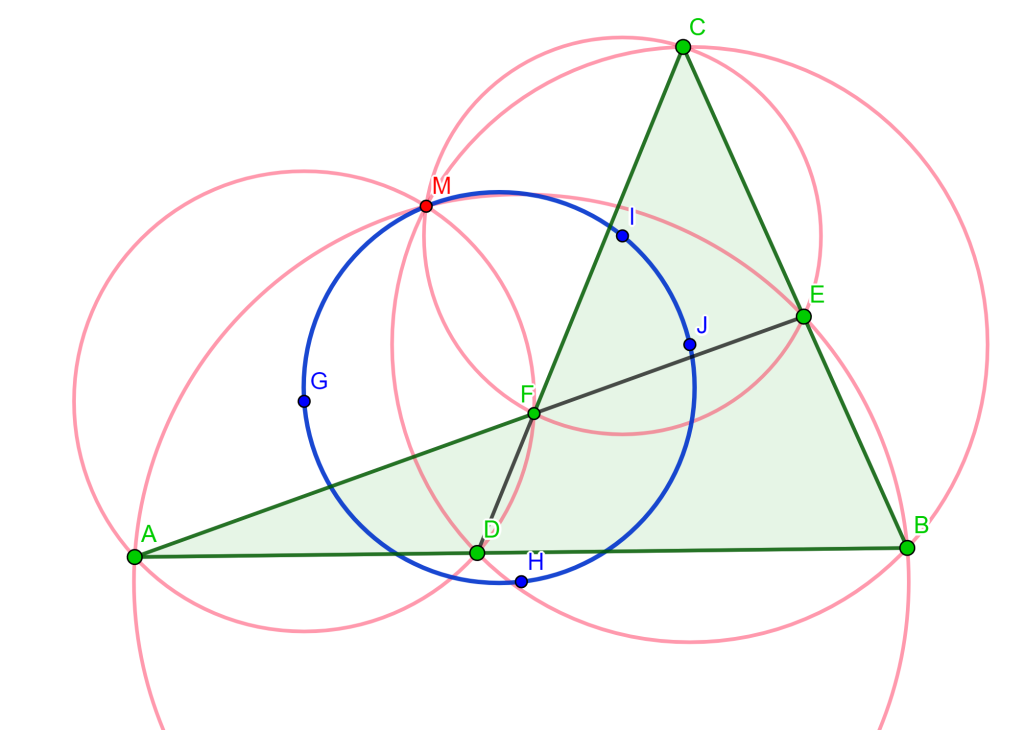
Círculo de Miquel

Respecto a las cuatro circunferencias del cuadrilátero completo con centros $O_1, O_2, O_3 $ y $O_4$ y el punto de Miquel $M$ son conciclicos. Por lo cual la circunferencia que contiene a estos cinco puntos se llama Círculo de Miquel.

Teoremas de la línea de Simson del punto de Miquel

Teorema. Sea una circunferencia circunscrita de un triángulo con un punto cualquiera de esta circunferencia, bajamos perpendiculares a los tres lados, entonces los pies de estas perpendiculares están en una línea recta (Línea de Simson).

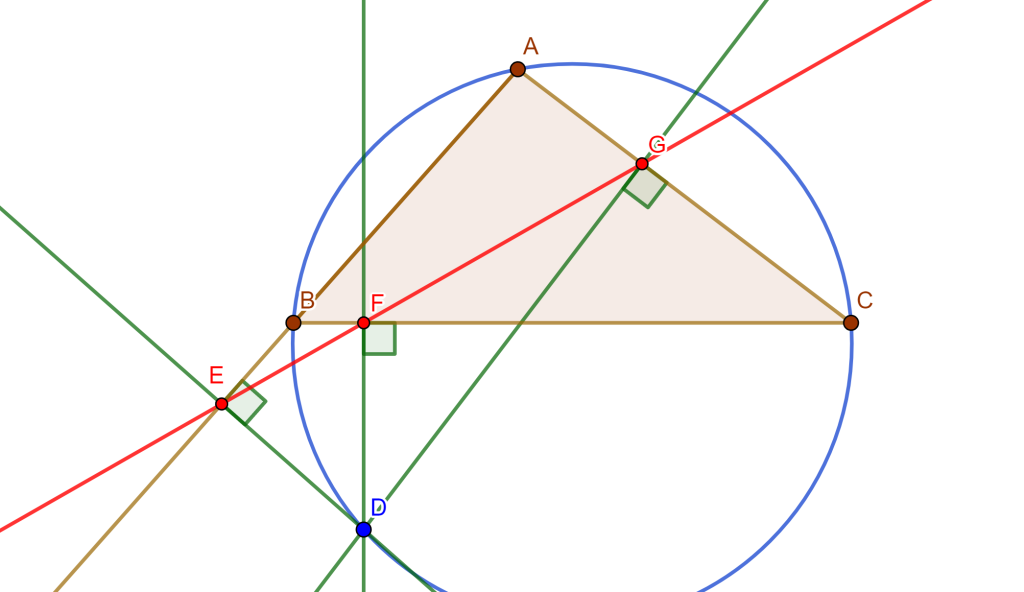
Teorema. Los pies de las perpendiculares de $M$ de los cuatro lados del cuadrilátero completo son colineales.

Teoremas del pentágono y los seis círculos de Miquel

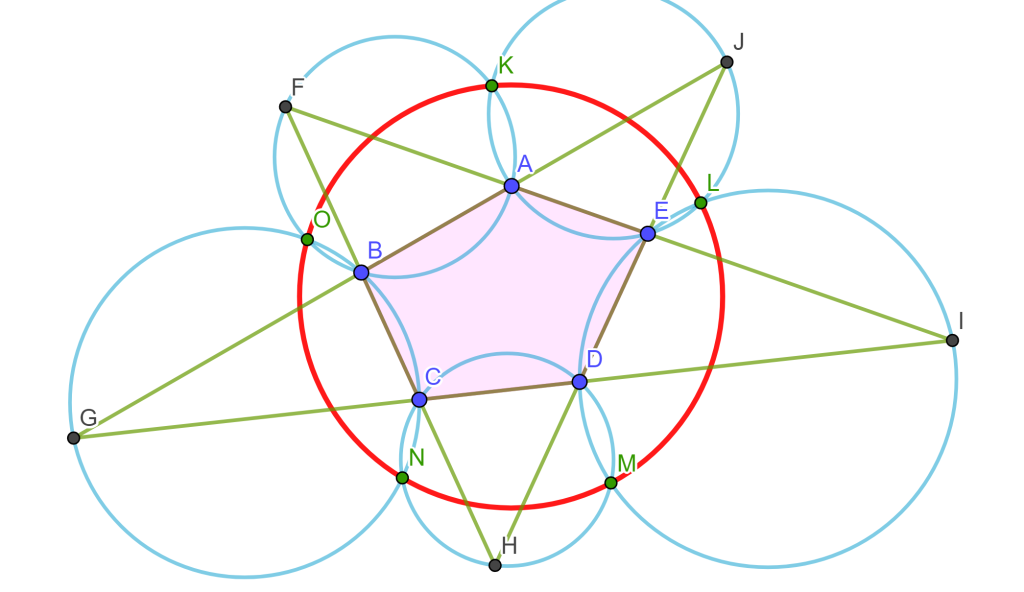
Teorema. (Pentágono) Sea $ABCDE$ un pentágono cualquiera, prolongando todos los lados, estos se intersecan en los puntos $F$, $G$, $H$, $I$ y $J$, entonces los puntos de intersección de las cinco circunferencias circunscritas $ABF$, $BCG$, $CDH$, $DEI$ y $EAJ$ son conciclicos.

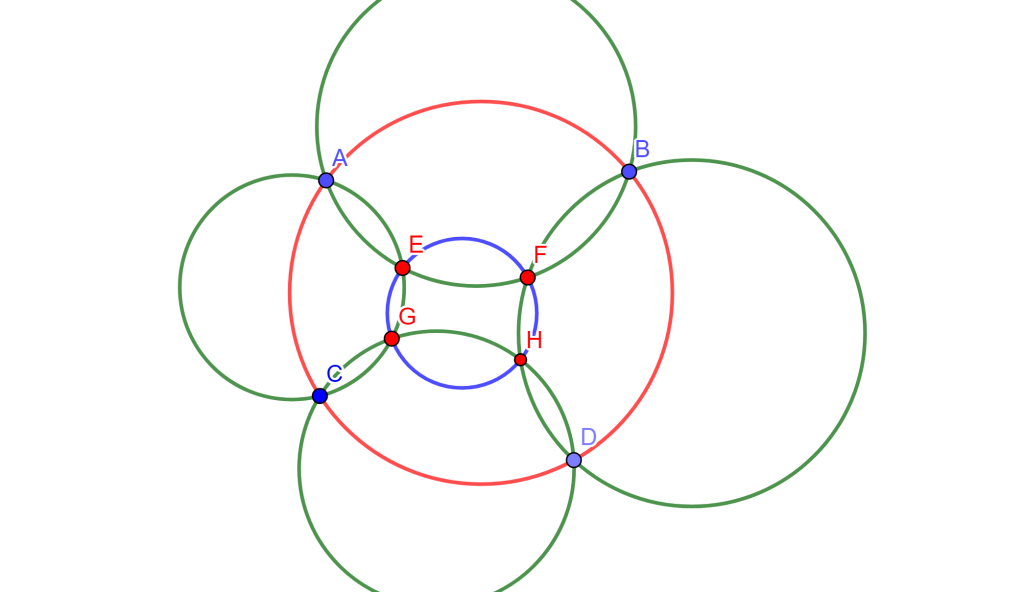
Teorema. (Seis Círculos) Sean los puntos $A$, $B$, $C$ y $D$ de una circunferencia y las circunferencias que pasan por los pares de puntos adyacentes, las intersecciones de estas circunferencias en $E$, $F$, $G$ y $H$ se encuentran en una sexta circunferencia en común.

Más adelante…

Al igual que los Teoremas de Miquel, se abordarán ahora los Teoremas de Carnot.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Teorema de Stewart
• Siguiente entrada del curso: Teorema de Carnot