Introducción
Uno de los temas más vistos en Geometría Moderna son las hileras de puntos y como estas se relacionan con varios temas, pero en este caso se verá su relación con la involución.
Hilera de puntos en Involución
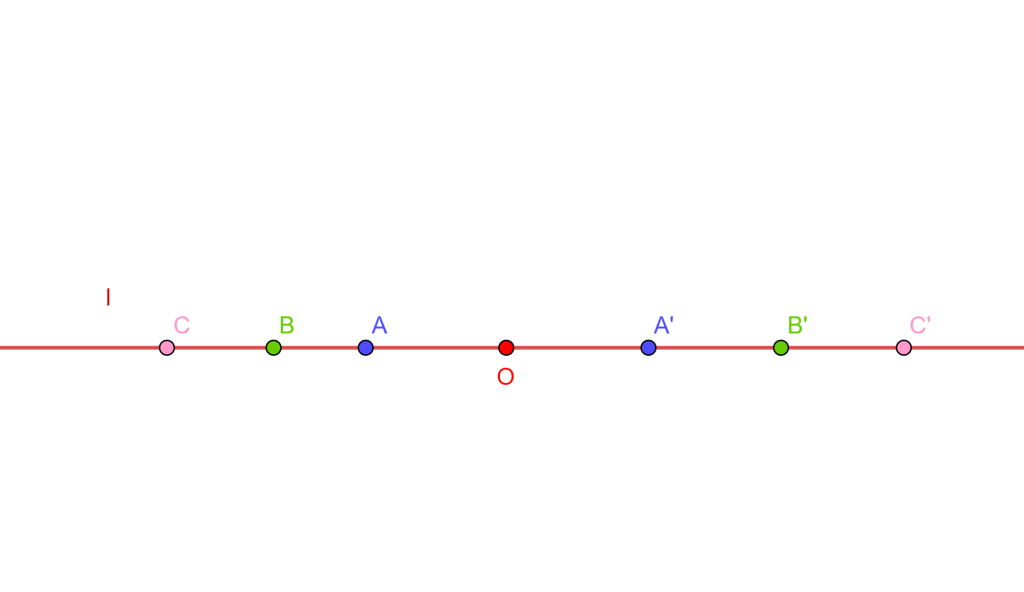
Sea una línea recta $l$ y un punto $O$ en la recta, sean los pares de puntos $A,A’,B,B’,C,C’$ ubicados en $l$ con respecto a $O$, de tal forma que $OA \bullet OA’ = OB \bullet OB’ = OC \bullet OC’$ entonces se dice que los puntos están en involución.
Donde $O$ es el centro de involución y los puntos por pares se llaman puntos conjugados y a $l$ se le denota como base de la involución. Y de esta forma se tiene una hilera en involución con respecto a $O$.
Se verá ahora un ejemplo de involución en una hilera de puntos.
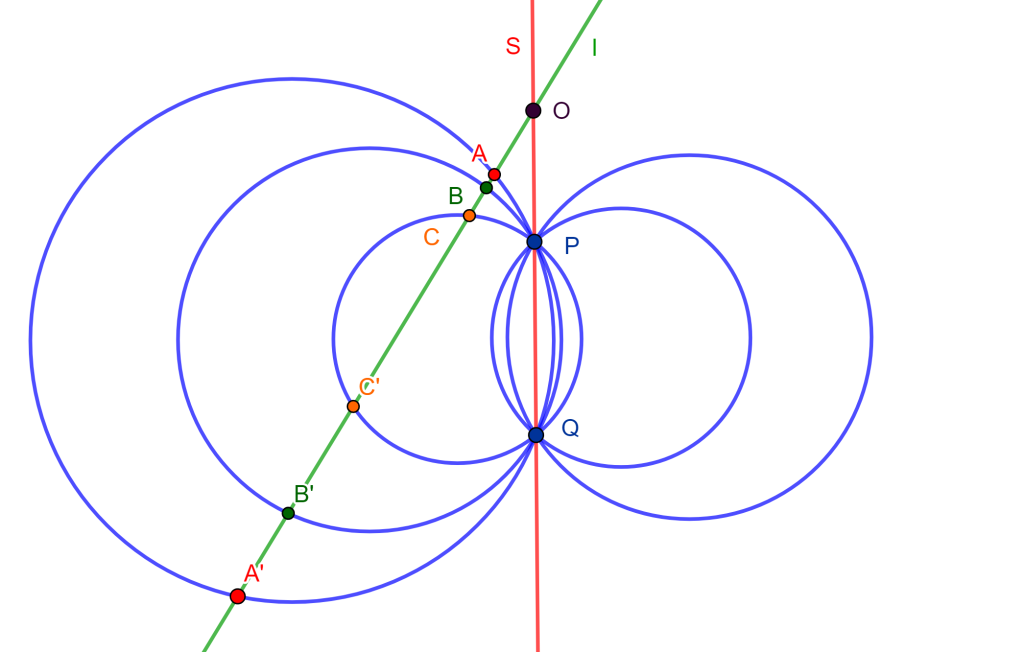
Ejemplo. Sea un conjunto de circunferencias coaxiales que se intersecan en $P$ y $Q$ con un eje radical «S».
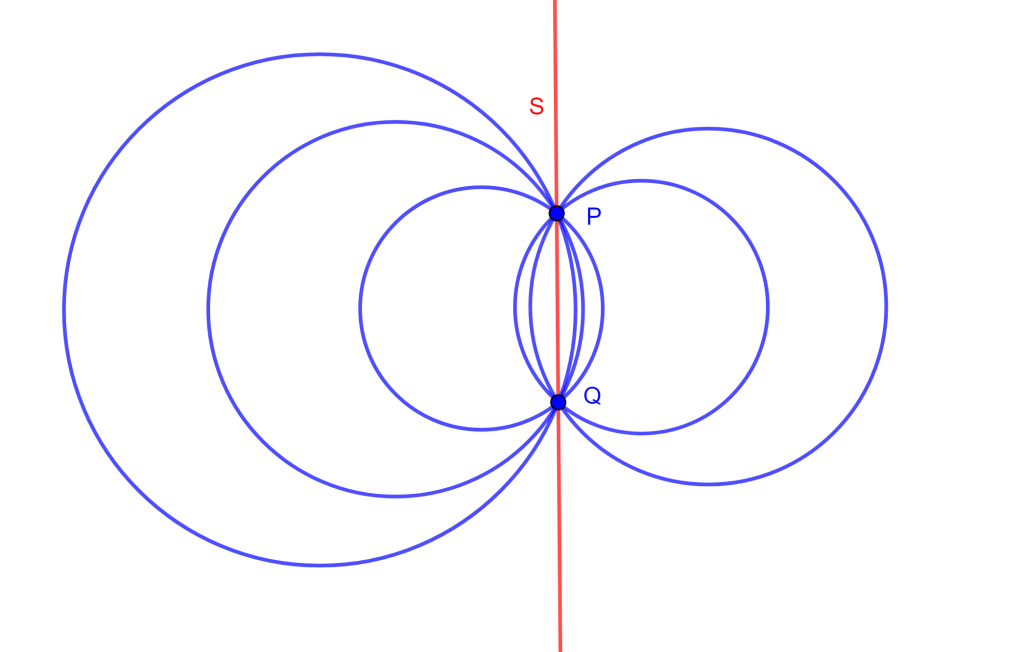
Sea $O$ un punto en el eje radical y tracemos una recta que pase por $O$ y distinto a «S», será una recta que llamaremos $l$. Las intersecciones con las circunferencias coaxiales forman pares de puntos conjugados, los cuales estarán en involución.
Y son conjugados los puntos por pares, ya que por propiedad de eje radical, la potencia de $O$ a cualquier elemento del sistema coaxial es el mismo. Entonces $OA \bullet OA’ = OB \bullet OB’ = OC \bullet OC’ = OP \bullet OQ$, de esta forma se tiene una hilera en involución.
$\triangle$
Ahora, si los pares de puntos de la recta están en un mismo lado de la recta «l» y el centro $O$, tienen el valor positivo al tener el mismo sentido los pares de puntos conjugados, pero si están en lados contrarios se tiene valor negativo.
Tipos de Involución
De esta forma se tienen dos tipos de involución.
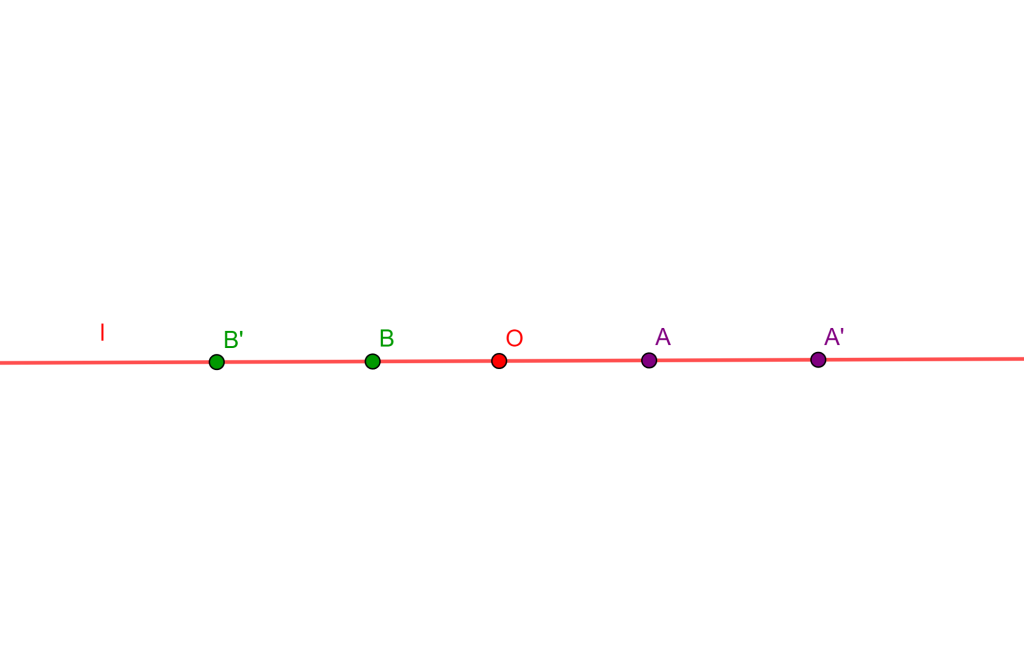
- Involución Hiperbólica: Cuando un par de puntos conjugados están en el mismo lado del centro de involución, de esta forma, si se tienen dos pares de puntos $A$ y $A’$ conjugados es hiperbólica si el producto $OA \bullet OA’$ es positivo.
- Involución Elíptica: Cuando un par de puntos conjugados están en lados opuestos del centro de involución, si se tienen dos pares de puntos $A$ y $A’$ conjugados es elíptica si el producto $OA \bullet OA’$ es negativo.
Proposiciones de Involución
Proposición. Sea una involución hiperbólica, entonces existen dos puntos $M$ y $N$ que son autoconjugados, es decir $OM^2 = ON^2 = OA \bullet OA’$
Demostración. Como se tiene una involución hiperbólica, entonces se tienen los pares de puntos $A$ y $A’$, $B$ y $B’$ conjugados de tal forma que $OA \bullet OA’ > 0$ y $OB \bullet OB’ > 0$, entonces existe un real positivo $k$ tal que $OA \bullet OA’ = k^2$. Si usamos a $k$ como radio con centro en $O$ este interseca a $l$ en dos puntos $M$ y $N$.
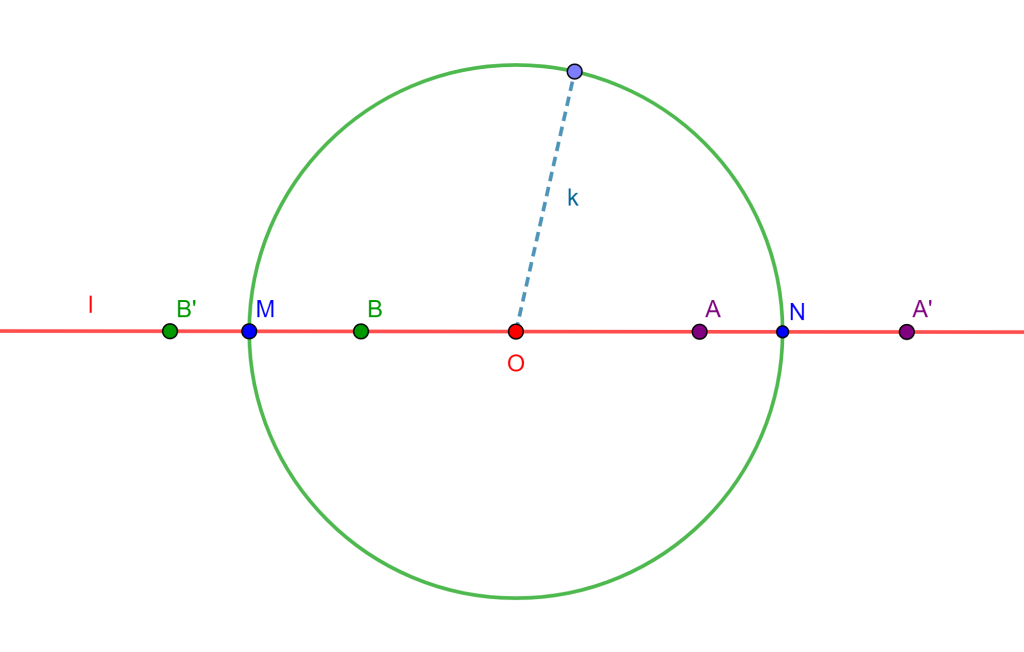
Y estos dos puntos $M$ y $N$ son los buscados, ya que $k=OM=ON$ entonces $k^2 = OM^2 = ON^2$, pero $OA \bullet OA’ = k^2$ y $OB \bullet OB’ = k^2$ entonces
$OA \bullet OA’ = OB \bullet OB’ = k^2 = OM^2 = ON^2.$
$\square$
Observaciones:
- $M$ y $N$ son conocidos como los puntos dobles de la involución.
- La involución elíptica no tiene puntos dobles.
- En una involución hiperbólica los puntos conjugados son inversos respecto a la circunferencia con diámetro $\bar{MN}$.
Proposición. Una involución elíptica de puntos puede trazarse en una línea recta por los lados de un ángulo recto que gira alrededor de su vértice.
Construcción. Sea una recta $l$ y un punto $O$ en esta, tracemos una recta $m$ perpendicular a $l$ que pase por $O$ y tomemos un punto $H$ en $m$.
Dibujemos una recta $a$ que pase por $H$ y corte a $O$ en el punto $A$, y para encontrar a su conjugado tracemos una recta $a’$ perpendicular a $a$ y pase por $H$, el punto de intersección con $l$ es $A’$.
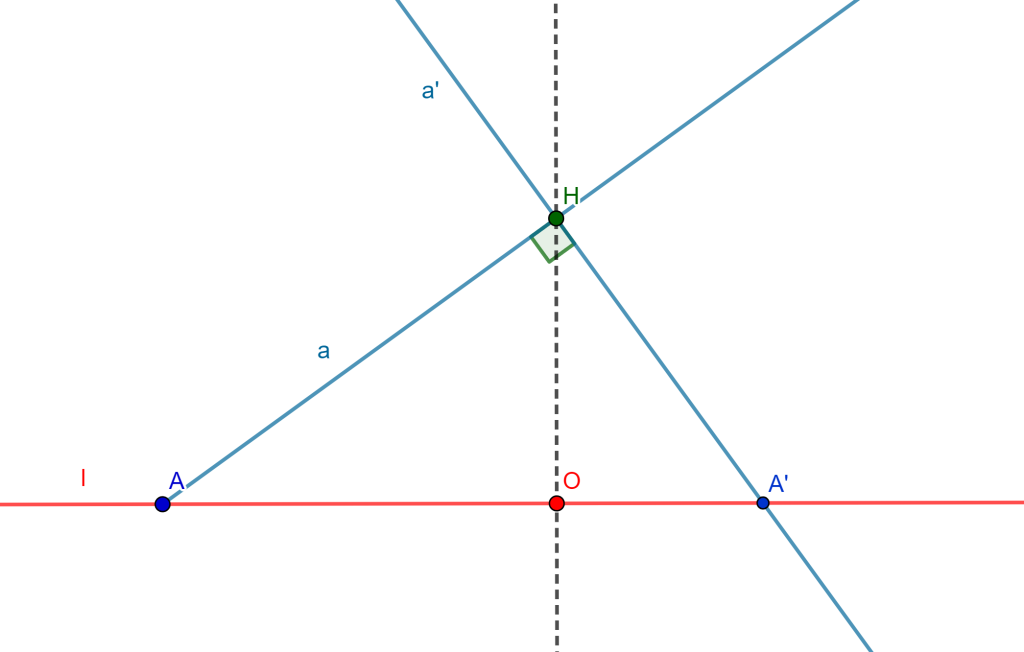
Observemos el triángulo $\triangle AHA’$ es un triángulo rectángulo y como se traza la altura $HO$ entonces se tienen dos triángulos semejantes $\triangle AOH \sim \triangle HOA’$. Por semejanza se tiene $\frac{\bar{AO}}{\bar{HO}} = \frac{\bar{OH}}{\bar{OA’}}$ entonces $\bar{AO} \bullet \bar{OA’} = \bar{OH} \bullet \bar{HO} = \bar{HO}^2 = HO^2$.
Y como son sentidos opuestos $AO$ y $OA’$ entonces $OA \bullet OA’ = – \bar{HO}^2$.
Donde $HO$ es una distancia fija (constante), por lo cual para cualquier otro par de puntos conjugados construidos de la misma forma que $A$ y $A’$, se tienen nuevos puntos conjugados.
$OB \bullet OB’ = -\bar{HO}^2$ y $OC \bullet OC’ = -\bar{HO}^2$
$\square$
Teoremas de Involución
Teorema. Dos pares de puntos conjugados de una involución determinan la involución.
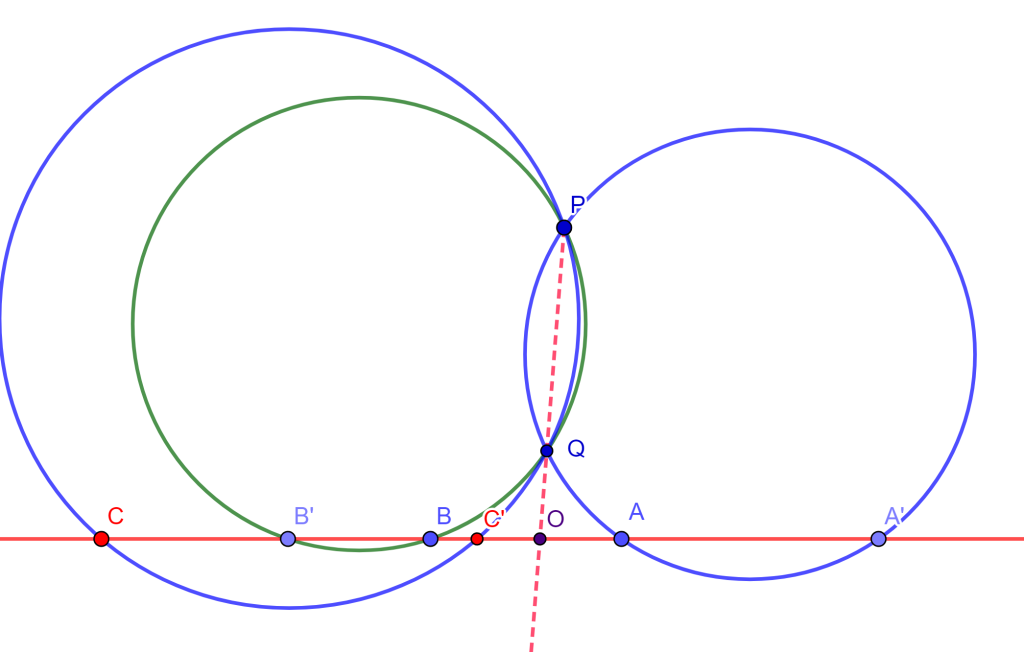
Demostración. Para ello sean $A, A’$ y $B, B’$ los dos pares de puntos conjugados en la recta $l$, y sea un punto arbitrario $C$ en $l$. Tomemos $P$ un punto fuera de la recta $l$, y tracemos las circunferencias que pasen por $P, A, A’$ y $P, B, B’$, a la otra intersección de estas dos circunferencias será $Q$.
Ahora si trazamos la circunferencia $PQC$ esta interseca a $l$ en un punto $C’$ y diremos que este es el conjugado de $C$, ya que al trazar la recta $PQ$ esta corta a $l$ en $O$ y por potencias $OP \bullet OQ = OA \bullet OA’ = OB \bullet OB’ = OC \bullet OC’ $. Además $C’$ es único, ya que solo existe una circunferencia por $PQC$, también $O$ es el centro de involución. Así es como se determina la involución.
$\square$
Teorema. La razón cruzada de cualesquiera cuatro puntos de una involución en la cual están presentes tres pares conjugados, es igual a la razón cruzada de sus cuatro conjugados.
Demostración. Tomemos tres pares de puntos conjugados $A, A’, B, B’$ y $C, C’$ de una involución de centro $O$, por definición de involución existe una constante $K=OA \bullet OA’ = OB \bullet OB’ = OC \bullet OC’ $.
Lo que se quiere demostrar es que tomando cualesquiera cuatro puntos $A, B, A’$ y $C’$ entonces $ \{ABA’C’ \} = \{ A’B’AC \}$ y por razón cruzada estos se puede ver como
$ \frac{AA’}{A’B} / \frac{AC’}{C’B} = \frac{A’A}{AB’} / \frac{A’C}{CB’}$
Por un lado, tenemos
$ \frac{AA’}{A’B} / \frac{AC’}{C’B} = \frac{AO + OA’}{A’O + OB} / \frac{AO + OC’}{C’O + OB} $
Además,
$K= OA \bullet OA’$ entonces $OA = \frac{K}{OA’}$ ó $OA’ = \frac{K}{OA}$
Esto sucede también para los pares $B,B’$ y $C, C’$.
$ \frac{AO + OA’}{A’O + OB} = \frac{\frac{K}{A’O} + \frac{K}{OA}}{\frac{K}{AO} + \frac{K}{OB’}} = \frac{K(OA + A’O) / A’O \cdot OA}{K(OB’ + AO) / AO \cdot OB’} = \frac{A’A}{AB’} \cdot \frac{OB’}{-A’O} = \frac{A’A}{AB’} \cdot \frac{OB’}{OA’}$
Por otro lado,
$ \frac{AO + OC’}{C’O + OB} = \frac{\frac{K}{A’O} + \frac{K}{OC}}{\frac{K}{CO} + \frac{K}{OB’}} = \frac{K(OC + A’O) / A’O \cdot OC}{K(OB’ + CO) / CO \cdot OB’} = \frac{A’C}{CB’} \cdot \frac{OB’}{OA’}$
Por lo cual
$ \frac{AA’}{A’B} / \frac{AC’}{C’B} = \frac{AO + OA’}{A’O + OB} / \frac{AO + OC’}{C’O + OB} = \frac{A’A}{AB’} \cdot \frac{OB’}{OA’} / \frac{A’C}{CB’} \cdot \frac{OB’}{OA’} = \frac{A’A}{AB’} / \frac{A’C}{CB’} = \{ A’B’AC \}$
Por lo tanto,
$ \{ABA’C’ \} = \{ A’B’AC \}.$
$\square$
Teorema. El inverso del teorema anterior dice, si seis puntos son relacionados por pares, y la razón cruzada de cuatro de ellos que representa los tres pares es igual a la razón cruzada de los cuatro puntos correspondientes, entonces los pares son pares conjugados de una involución.
Más adelante…
Se analizará ahora los haces de líneas en involución, así como propiedades y teoremas.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Teoremas de Pascal, Brianchon y Pappus
- Siguiente entrada del curso: Haces de líneas en Involución