Geometría Moderna II: Haces de líneas en Involución

Introducción

A partir de la involución en una hilera de puntos y sus puntos conjugados relacionados con la razón cruzada, es que nace el concepto de haces de líneas en involución. Muchos de los resultados que se muestran son gracias al principio de dualidad.

Haces de líneas en involución

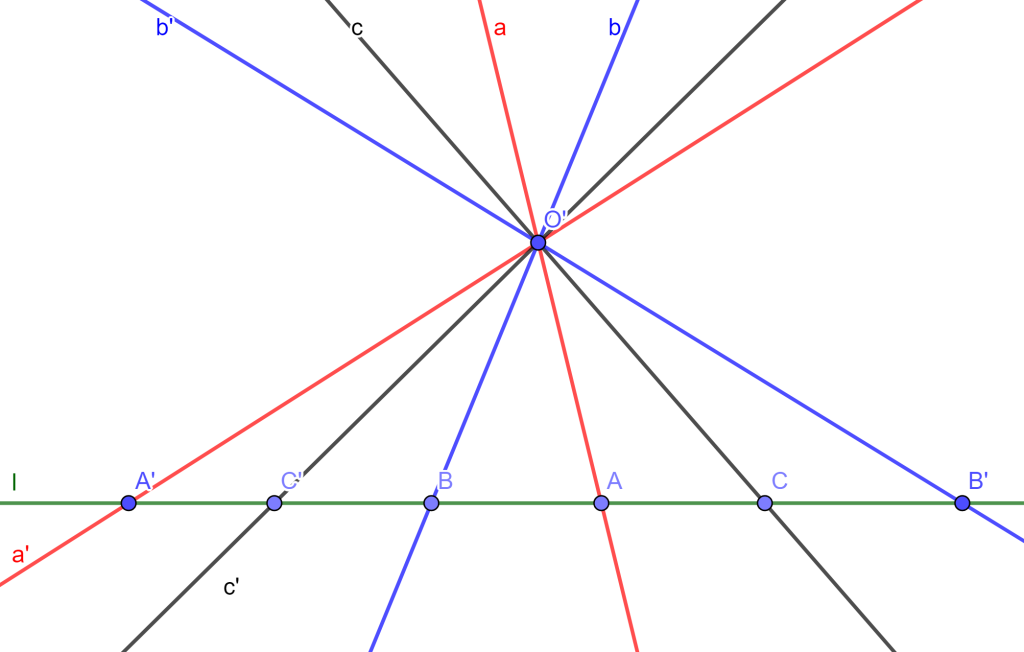
Definición. Dado un haz de rectas correlacionadas por parejas y donde los puntos de intersección de los pares con cualquier transversal que no pase por el vértice del haz son pares conjugados de una involución de puntos.

Ejemplo: Sean el haz con las rectas correlacionadas por pares $a, a^{'}, b, b^{'}, c$ y $c^{'}$ . Tracemos una recta que corte al haz de rectas y que no pase por $O^{'}$ , se tienen las intersecciones $A, A^{'}, B, B^{'}, C$ y $C^{'}$ y donde estos son pares de puntos conjugados de una involución. De esta forma se tiene un haz de rectas en involución.

$△$

Propiedades

Al igual que en las hileras de puntos dobles, entonces las rectas del haz que pasan por estos puntos se les llamaran rectas dobles de la involución

Las dos rectas que pertenecen al mismo par se llaman rectas conjugadas.
De la misma forma en que se tienen los dos tipos de involución hiperbólica y elíptico, estos serán usados con haces de líneas en involución en el mismo sentido que el uso con hileras de puntos en involución.
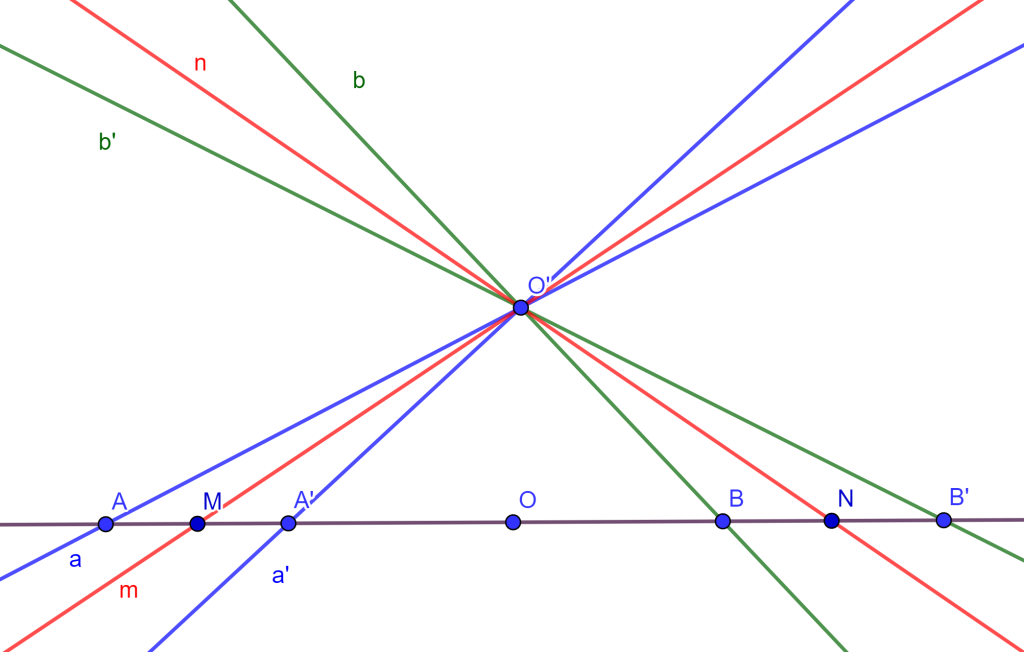
Del teorema de razón cruzada en la involución, el cual dice «La razón cruzada de cualesquiera cuatro puntos de una involución en la cual están presentes tres pares conjugados, es igual a la razón cruzada de sus cuatro conjugados» nos da la siguiente propiedad si un haz de líneas corta cualquier transversal en una involución, cortará cualquier transversal que no pase por su vértice en una involución.

Ejemplo. Se tiene la razón cruzada y la igualdad ${A C A^{'} B} = {A^{'} C^{'} A B^{'}}$ y como se tiene el haz en involución, entonces cuando corte a la transversal $l^{'}$ se tendrán las siguientes igualdades de razón cruzada:
${A C A^{'} B} = {A_{1} C_{1} A_{1}^{'} B_{1}}$ y ${A^{'} C^{'} A B^{'}} = {A_{1}^{'} C_{1}^{'} A_{1} B_{1}^{'}}$
Y por la igualdad de ${A C A^{'} B} = {A^{'} C^{'} A B^{'}}$ , entonces ${A_{1} C_{1} A_{1}^{'} B_{1}} = {A_{1}^{'} C_{1}^{'} A_{1} B_{1}^{'}}$ .
Lo cumple el teorema de razón cruzada con involución, por lo tanto, los puntos de $l^{'}$ están en involución respecto al punto $O_{1}^{'}$ .

$△$

Haz en involución y el vértice en la circunferencia

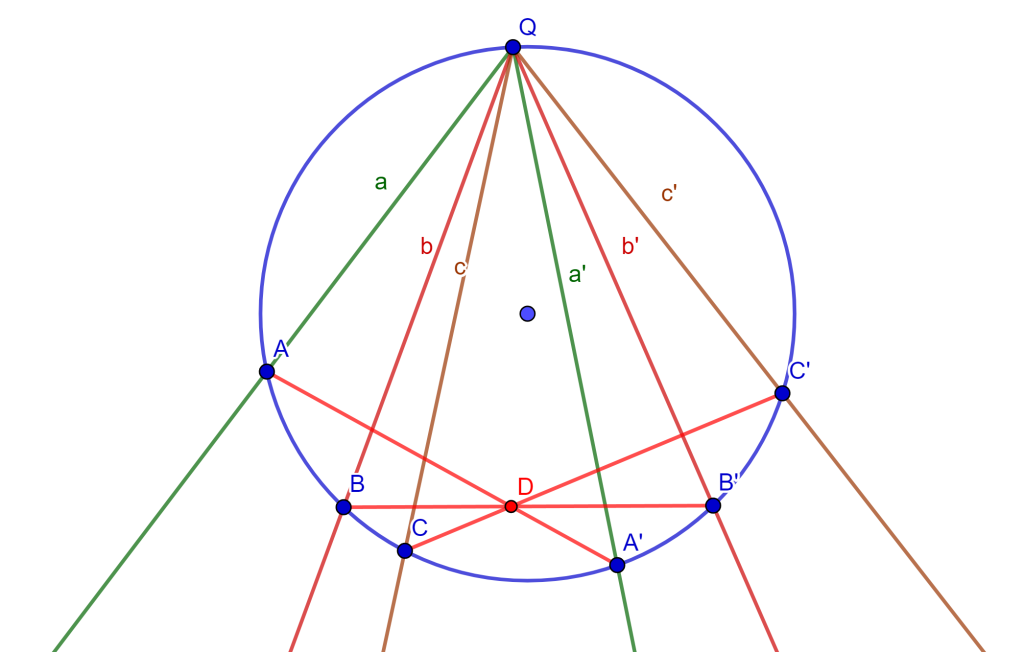
Teorema. Sea un haz de rectas en involución donde se tienen los pares conjugados $a, a^{'}, b, b^{'}, c, c^{'}$ y que tienen su vértice en una circunferencia, y si estas rectas cortan la circunferencia nuevamente en $A, A^{'}, B, B^{'}, C, C^{'}$ respectivamente, entonces las rectas $A A^{'}, B B^{'}, C C^{'}$ son concurrentes.

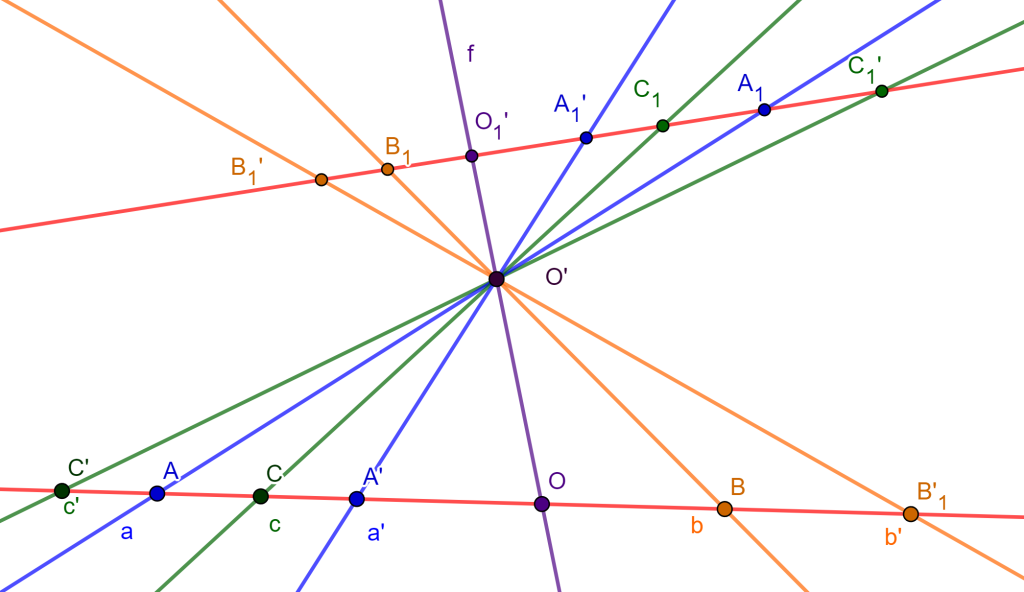
Demostración. Tracemos una recta $l$ que corte al haz y no pase por $Q$ , nos da las intersecciones $A_{1}, B_{1}, C_{1}, A_{1}', B_{1}', C_{1}^{'}$ .

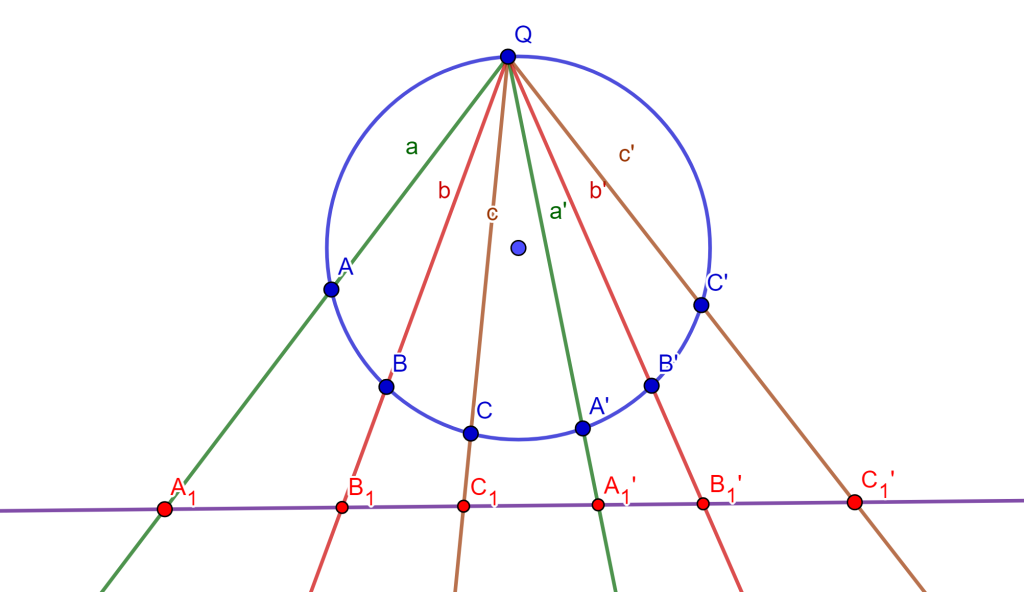
Haces de líneas en circunferencia e hilera en involución

Como los haces de líneas está en involución y cualquier recta que corte al haz nos da una hilera de puntos en involución, por el teorema de razón cruzada con hilera de puntos nos da la siguiente igualdad.

${A_{1} A_{1}^{'} B_{1} C_{1}} = {A_{1}^{'} A_{1} B_{1}^{'} C_{1}^{'}}$

Por propiedades de razón cruzada se cumple:

${a a^{'} b c} = {a^{'} a b^{'} c^{'}}$

Se puede decir que la propiedad de razón cruzada también se cumple para haz de rectas en involución, es decir, que cualesquiera cuatro rectas que tiene de esa involución la razón cruzada va a ser a la de sus correspondientes.
Observemos que estos haces salen a partir del punto $Q$ y pasan por los puntos de intersección con la circunferencia. Entonces se puede poner el haz desde $Q$ :

$Q {A A^{'} B C} = Q {A^{'} A B^{'} C^{'}}$

Y va a ser lo mismo si cambiamos $Q$ por $B^{'}$ y $C$ :

$B^{'} {A A^{'} B C} = C {A^{'} A B^{'} C^{'}}$

Tracemos las rectas $A A^{'}$ , $B B^{'}$ y $C C^{'}$ , y tracemos la recta $B^{'} C$ , donde se tienen las intersecciones con $A A^{'}$ que son $X, Y$ y $Z$ . Por demostrar que $X = Y$ .

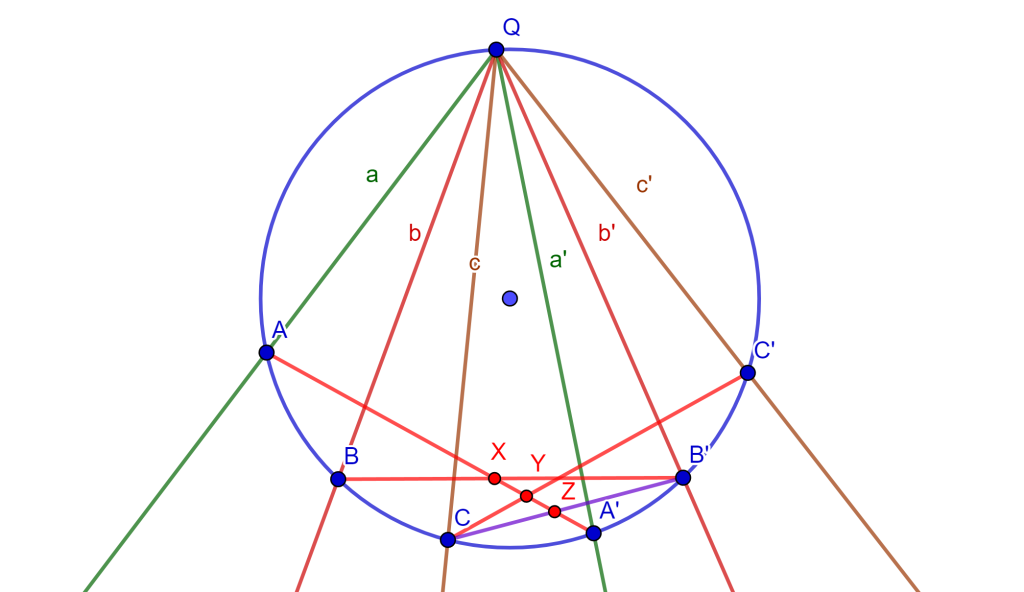
La razón cruzada de $B^{'} {A A^{'} B C} = B^{'} {A A^{'} X Z}$ y, por otro lado, $C {A^{'} A B^{'} C^{'}} = C {A^{'} A Z Y}$ , entonces ${A A^{'} X Z} = {A^{'} A Z Y}$ . De esta igualdad se tienen tres puntos iguales $A^{'}, A$ y $Z$ , y el cuarto punto $X$ y $Y$ deben ser iguales, ya que si intercambiamos dos puntos de esta razón cruzada, los otros dos también deben intercambiarse, para que se conserve la razón cruzada entonces se tiene la igualdad:

${A A^{'} X Z} = {A A^{'} Y Z}$

Por lo cual $X = Y$ y se concluye que las rectas $A A^{'}$ , $B B^{'}$ y $C C^{'}$ son concurrentes.

Del resultado anterior se puede generar la duda de que pasa si la involución es hiperbólica o elíptica, por ende se debe definir de manera más formal.

Definición. Sea $a, a^{'}, b, b^{'}, c, c^{'}$ los haces de líneas en involución y una recta $l$ que no pase por el vértice $Q$ del haz, la cual generara intersecciones con el haz, las cuales son $A, A^{'}, B, B^{'}, C, C^{'}$ respectivamente.

Si $A, A^{'}, B, B^{'}, C, C^{'}$ es una involución elíptica, se dice que el haz está en involución elíptica.
Si $A, A^{'}, B, B^{'}, C, C^{'}$ es una involución hiperbólica, se dice que el haz está en involución hiperbólica.

Rectas Conjugadas en ángulos rectos

Teorema. En un haz de rectas en involución siempre hay un par de rectas conjugadas perpendiculares entre sí, por otra parte, si existe más de un par de rectas conjugadas en ángulos rectos, entonces todos los pares conjugados son perpendiculares entre sí y la involución es elíptica.

Demostración. Sea un haz de rectas en involución $a, a^{'}, b, b^{'}, c, c^{'}$ con $Q$ vértice, tracemos una circunferencia con centro $O$ que pase por $Q$ y el haz corte a la circunferencia en los puntos $A, A^{'}, B, B^{'}, C, C^{'}$ respectivamente al orden que se mencionó las rectas.
Por el teorema anterior se afirma que las rectas $A A^{'}, B B^{'}, C C^{'}$ son concurrentes en $X$ . Tracemos la recta $X O$ , la cual corta a la circunferencia en dos puntos $D$ y $D^{'}$ los cuales son puntos extremos del diámetro $D D^{'}$ . Si trazamos las rectas $D Q$ y $D^{'} Q$ nos forma un ángulo recto $∠ D Q D^{'}$ .

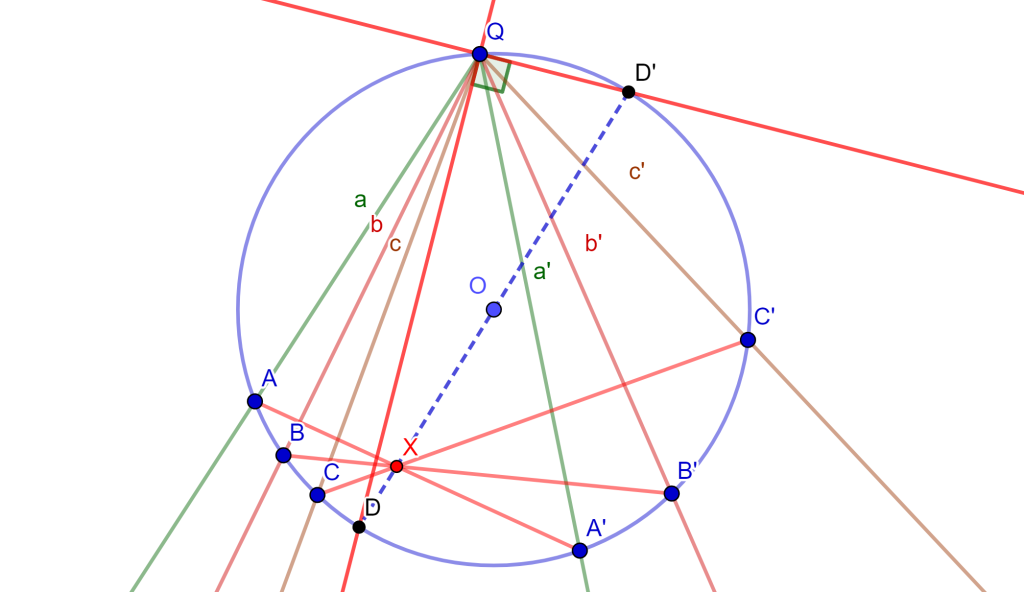
Por demostrar que las rectas $D Q$ y $D^{'} Q$ son un par conjugado de la involución. Tracemos una recta $l$ que corte al haz $a, a^{'}, b, b^{'}, c, c^{'}$ en involución en los puntos $A_{1}, A_{1}', B_{1}, B_{1}', C_{1}, C_{1}^{'}$ respectivamente, además corta a las rectas $Q D$ y $Q D^{'}$ en $D_{1}$ y $D_{1}^{'}$ respectivamente.

Tenemos que ver que los pares $D_{1}$ y $D_{1}^{'}$ están en la hilera de puntos en involución, entonces supongamos que $D_{1}$ tiene su par conjugado en la involución $D_{1}^{'}$ $^{'}$ , se quiere demostrar que $D_{1}^{'} = D_{1}^{'}$ $^{'}$ . Por teorema de razón cruzada en involución se tienen las siguientes igualdades:

${A_{1} B_{1} C_{1} D_{1}} = {A_{1}^{'} B_{1}^{'} C_{1}^{'} D_{1}^{'}$ $^{'}}$ y ${A_{1} B_{1} C_{1} D_{1}} = Q {A B C D}$ .

Ahora en razón cruzada nos dice que si cuatro secantes que pasan por un punto $X$ y al observar la razón cruzada del haz formado por un punto $Q$ en la circunferencia con los puntos $A, B, C, D$ debe ser la misma razón cruzada del haz con los puntos correspondientes de la secante ósea $A^{'}, B^{'}, C^{'}, D^{'}$ , lo cual da la igualdad:

$Q {A B C D} = Q {A^{'} B^{'} C^{'} D^{'}}$ y ademas $Q {A^{'} B^{'} C^{'} D^{'}} = {A_{1}^{'} B_{1}^{'} C_{1}^{'} D_{1}^{'}}$ .

Por lo cual da la igualdad:

${A_{1}^{'} B_{1}^{'} C_{1}^{'} D_{1}^{'}$ $^{'}} = {A_{1} B_{1} C_{1} D_{1}} = Q {A B C D} = Q {A^{'} B^{'} C^{'} D^{'}} = {A_{1}^{'} B_{1}^{'} C_{1}^{'} D_{1}^{'}}$

Entonces ${A_{1}^{'} B_{1}^{'} C_{1}^{'} D_{1}^{'}$ $^{'}} = {A_{1}^{'} B_{1}^{'} C_{1}^{'} D_{1}^{'}}$ por ende $D_{1}^{'} = D_{1}^{'}$ $^{'}$ , se concluye que $D Q$ y $D^{'} Q$ son un par conjugado perpendicular de la involución.

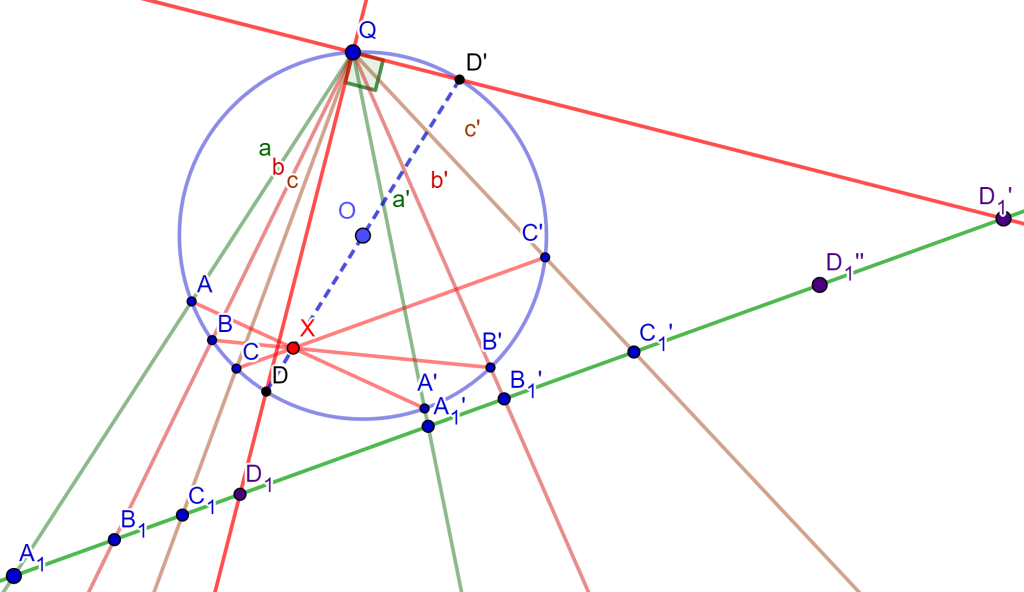
Ahora, si existe otro par de rectas conjugadas en ángulos rectos, las cuales supongamos que son $b$ y $b^{'}$ , esto nos diría que sus puntos $B$ y $B^{'}$ son diametralmente opuestos, por lo cual, las rectas $D D^{'}$ y $B B^{'}$ se cortan en el centro $O$ .
Y como se tiene el haz de rectas conjugadas en involución $a, a^{'}, D Q, D^{'} Q, b, b^{'}$ entonces las rectas $A A^{'}, D D^{'}$ y $B B^{'}$ son concurrentes, pero como $D D^{'}$ y $B B^{'}$ se cortan en $O$ entonces también $A A^{'}$ pasa por $O$ . Se concluye que todos los pares conjugados son perpendiculares entre sí y la involución es elíptica.

Teoremas relacionados con los haces de líneas en involución

Se mencionarán tres teoremas, los cuales se dejaran como ejercicios a resolver.

Teorema. Dado un cuadrángulo completo, sus tres pares de lados opuestos son intersecados por cualquier transversal que no pasa por un vértice en tres pares de puntos conjugados de una involución.

Teorema. Sea un cuadrángulo inscrito en una circunferencia, cualquier recta que no pase por un vértice, corta a la circunferencia y los pares de lados opuestos del cuadrángulo en una involución.

Teorema. Si dos pares de lados opuestos de un cuadrángulo completo son ortogonales, el tercer par es también ortogonal.

Más adelante…

Se dejarán los ejercicios correspondientes a esta unidad de Razón Cruzada.

Entradas relacionadas

Ir a Geometría Moderna II
Entrada anterior del curso: Hileras de puntos en involución
Siguiente entrada del curso: Ejercicios Unidad 4

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Geometría Moderna II: Haces de líneas en Involución

Introducción

Haces de líneas en involución

Propiedades

Haz en involución y el vértice en la circunferencia

Rectas Conjugadas en ángulos rectos

Teoremas relacionados con los haces de líneas en involución

Más adelante…

Entradas relacionadas

Me gusta esto:

Deja una respuesta Cancelar la respuesta

Introducción

Haces de líneas en involución

Propiedades

Haz en involución y el vértice en la circunferencia

Rectas Conjugadas en ángulos rectos

Teoremas relacionados con los haces de líneas en involución

Más adelante…

Entradas relacionadas

Comparte esto:

Me gusta esto:

Deja una respuesta Cancelar la respuesta