Introducción
Se analizó el concepto de razón cruzada como ${ABCD}= \lambda$ dados cuatro puntos colineales, pero existen veinticuatro permutaciones de estos cuatro puntos, por lo cual se tienen razones cruzadas para cada una de estas. El detalle está en que se pueden agrupar solo en seis tipos de razón cruzada.
Proposición. Dados cuatro puntos colineales distintos $A,B,C$ y $D$ en una recta $l$ y ${ABCD}= \lambda$.
Se tienen seis tipos de razón cruzada:
- ${ABCD}={BADC}={CDAB}={DCBA}=\lambda$
- ${ABDC}={BACD}={CDBA}={DCAB}=1/\lambda$
- ${ACBD}=1- \lambda$
- ${ACDB}=\frac{1}{1-\lambda}$
- ${ADBC}=\frac{\lambda-1}{\lambda}$
- ${ADCB}=\frac{\lambda}{\lambda-1}$
Construcción del cuarto elemento
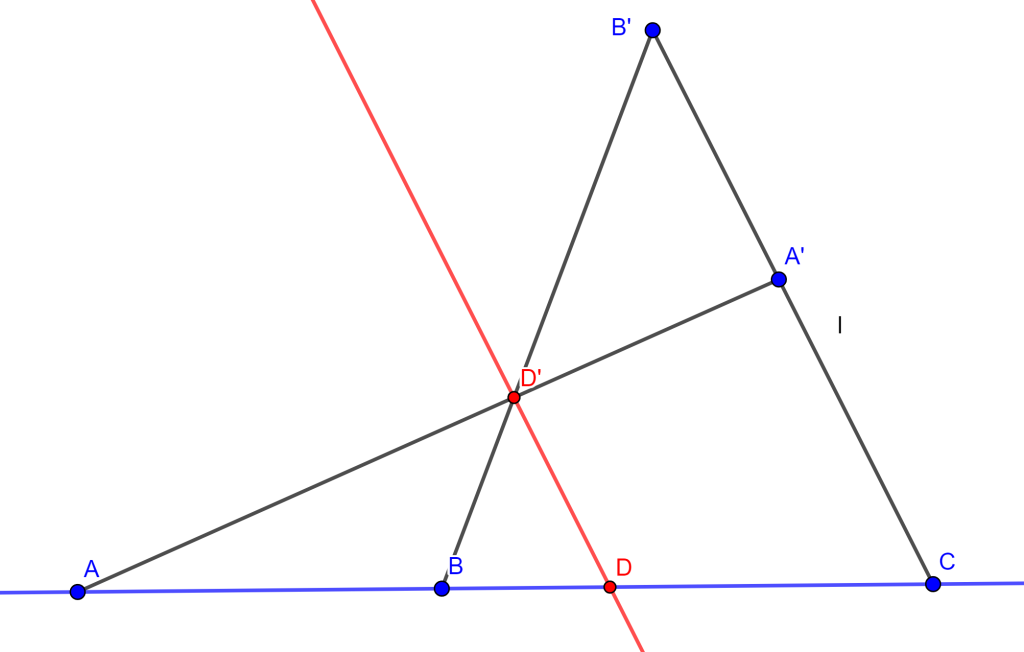
Dados tres puntos $A,B,C$ colineales distintos, se requiere construir un cuarto punto $D$ colineal con ellos tal que ${ABCD}=\lambda$.
Sea $l$ cualquier recta por $C$, sobre esta tomemos dos puntos $A’$ y $B’$ tales que $CA’/CB’=\lambda$. Ahora unimos $B’$ con $B$ y $A’$ con $A$, de tal forma que $AA’ \cap BB’=D’$, y por este punto de intersección trácese la paralela a $CB’$ que interseque la recta $x$ por $D$. Es decir, $DD’ \parallel CB’ = l$.
Por demostrar ${ABCD}=\frac{AC}{CB}/\frac{AD}{DB}=\lambda$.
Demostración. Se tiene que los triangulos $\triangle B’BC \sim \triangle D’BD$, $\triangle A’AC \sim \triangle D’AD$, por lo cual:
$\frac{B’C}{D’D}=\frac{BC}{BD}$ y $\frac{A’C}{D’D}=\frac{AC}{AD}$.
Entonces
$\frac{CB’}{D’D}=\frac{CB}{DB}$ y $\frac{CA’}{DD’}=\frac{AC}{AD}$.
Entonces
$\frac{AC}{AD}/\frac{CB}{DB}=\frac{CA’}{DD’}/\frac{CB’}{DD’}=\frac{CA’}{DD’}=\lambda$.
Por lo tanto, $\frac{AC*DB}{AD*CB}={ABCD}=\lambda$.
$\square$
Más adelante…
Se analizará la razón cruzada en la circunferencia.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Unidad 4 Razón Cruzada
- Siguiente entrada del curso: Razón cruzada en la circunferencia