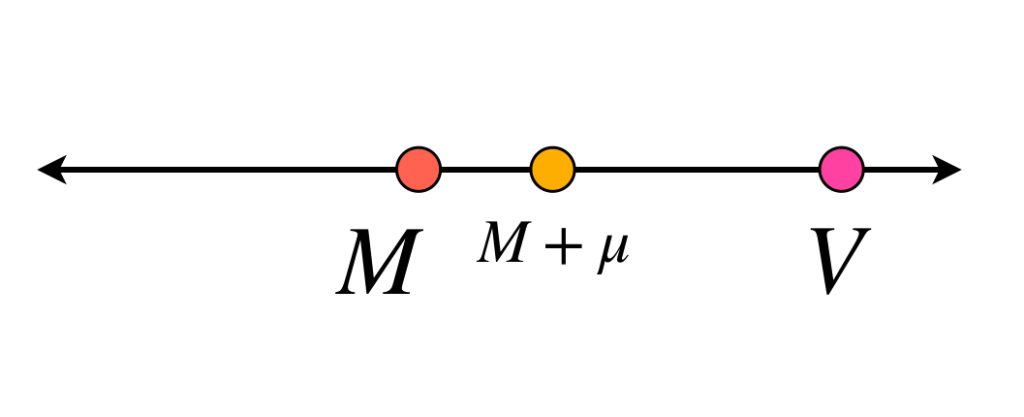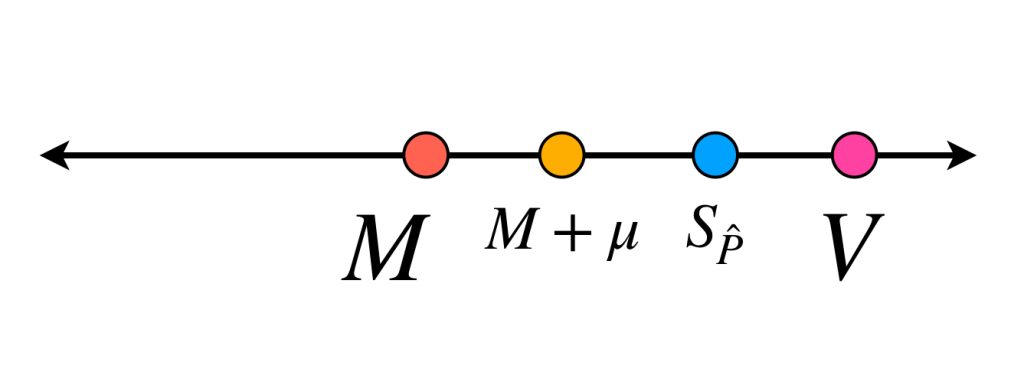$\textit{MATERIAL EN REVISIÓN}$
Introducción
El contenido de esta sección se basa predominantemente en el libro
Wheeden, R.L., Zygmund, A., Measure and Integral. An Introduccion to Real Analysis. (2da ed.). New York: Marcel Dekker, 2015, págs 22-26.
Tal como lo hicimos en la entrada anterior, seguiremos hablando de las funciones de variación acotada. Notemos que en los resultados de esta teoría no suele pedirse que la función sea continua o acotada, más aún, esto pudiera no ser suficiente para que una función sea de variación acotada, tal como lo muestra un ejercicio de la tarea moral de esta sección. Veamos entonces qué hipótesis pudieran ser útiles. Comencemos con la siguiente:
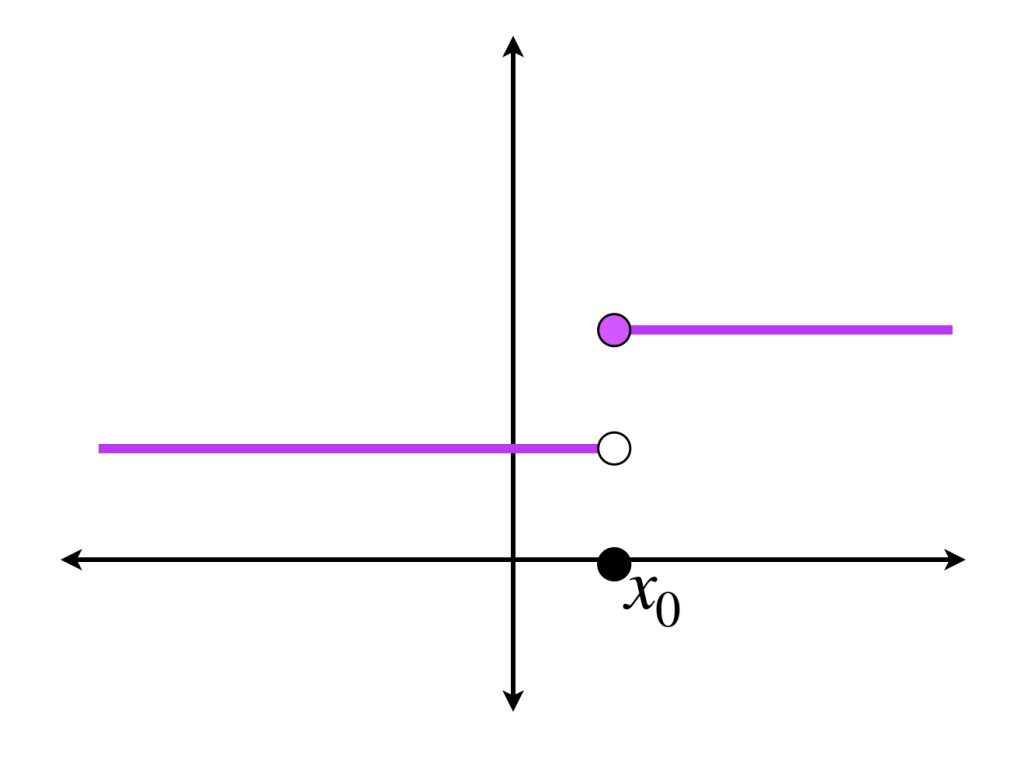
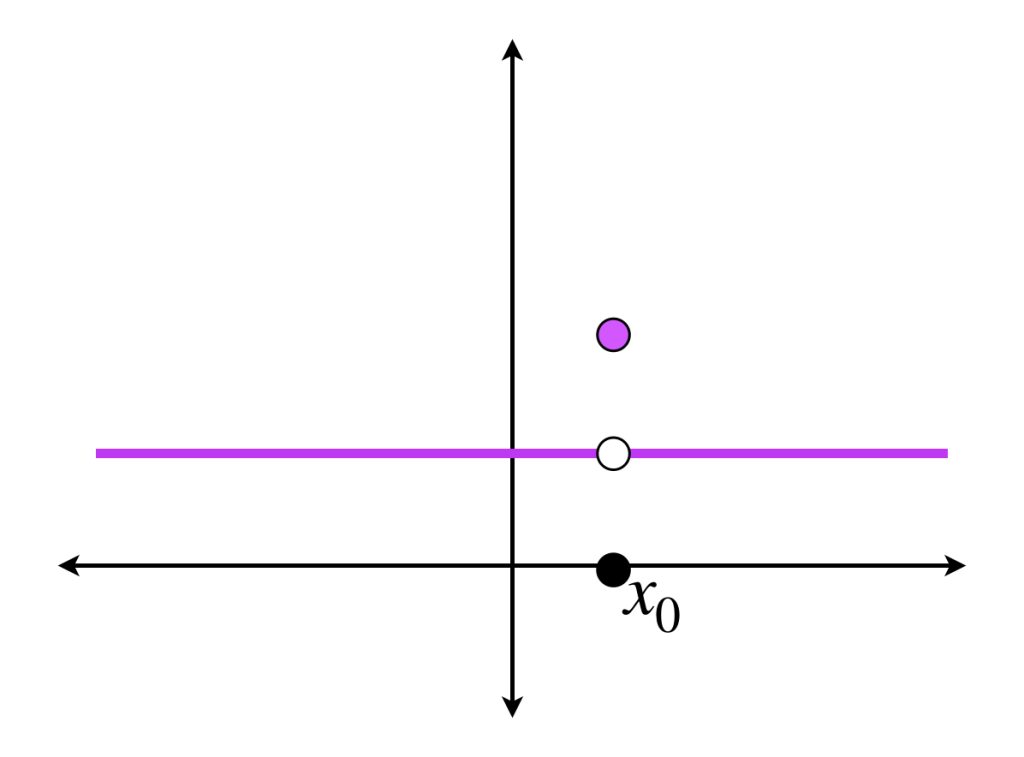
Definición. Discontinuidades del primer tipo. Sea $f: \mathbb{R} \to \mathbb{R}$ y sea $x_0 \in \mathbb{R}.$ En los siguientes dos casos, $f$ no es continua en $x_0.$
a) Cuando $\underset{x \to x_0 ^+}{lim} \, f(x)$ y $\underset{x \to x_0 ^-}{lim} \, f(x)$ existen y son distintos de $\infty$ pero
$$\underset{x \to x_0 ^+}{lim} \, f(x) \neq\underset{x \to x_0 ^-}{lim} \, f(x).$$
b) Cuando $\underset{x \to x_0 ^+}{lim} \, f(x)$ y $\underset{x \to x_0 ^-}{lim} \, f(x)$ existen y son distintos de $\infty$ y además
$$\underset{x \to x_0 ^+}{lim} f(x) = \underset{x \to x_0 ^-}{lim} \, f(x)$$
pero $ \underset{x \to x_0 }{lim} f(x) \neq f(x_0).$
En cualquiera de estas situaciones, diremos que $f$ tiene una discontinuidad del primer tipo en $x_0.$
Proposición. Sea $f:[a,b] \to \mathbb{R} \,$ una función de variación acotada en $[a,b],$ entonces tiene a lo más una cantidad numerable de discontinuidades y todas son del primer tipo.
Demostración:
Sea $f$ de variación acotada. De acuerdo con la entrada anterior, $f$ es acotada en $[a,b]$. Veamos un caso bonito en el que $f$ es creciente.
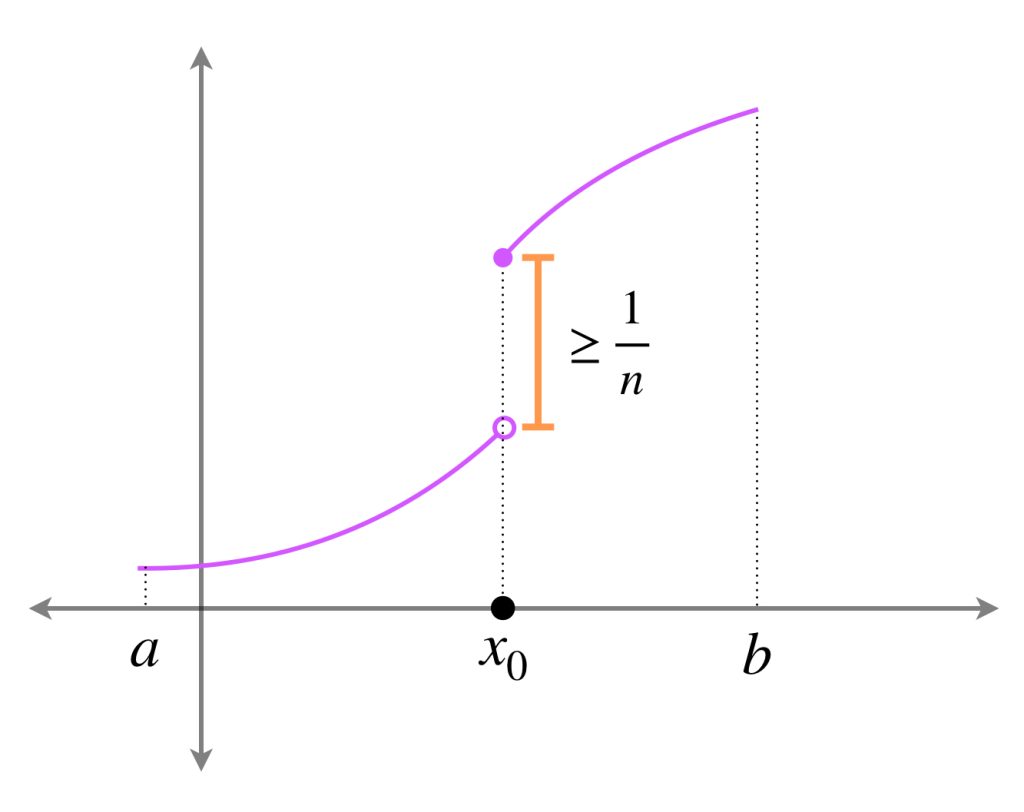
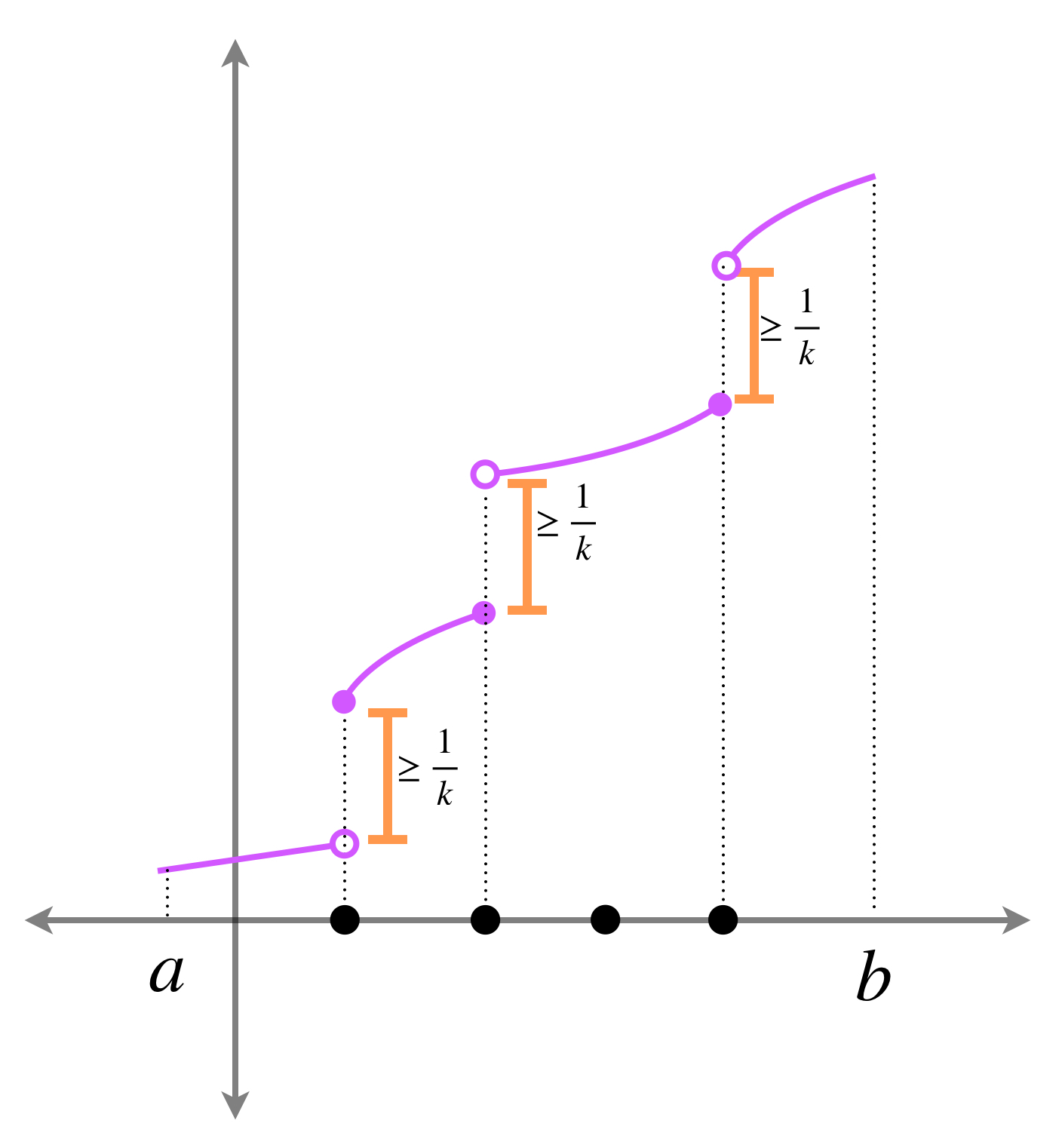
El conjunto de discontinuidades de $f$ puede expresarse como
$$D := \underset{n \in \mathbb{N}}{\bigcup} \, \left\{x_0 : \underset{x \to x_0 ^+}{lim} f(x) \, – \, \underset{x \to x_0 ^-}{lim} \, f(x) \geq \frac{1}{n} \right\}$$
pues el «tamaño del salto» en una discontinuidad siempre será mayor que algún $\frac{1}{n}$ suficientemente pequeño.
Nota que cada uno de los conjuntos que compone la unión es o bien finito o vacío, (pues para cada $k \in \mathbb{N} \,$ el segmento $\frac{1}{k}$ cabe un número finito de veces en la altura $f(b) \, – \, f(a)$), por lo tanto, $D$ es contable.
Ahora veamos el caso general. De acuerdo con el teorema de Jordan, visto al final de la entrada anterior,
$$f = f_1 \, – \, f_2,$$
con $f_1$ y $f_2$ funciones crecientes y acotadas que, por lo que acabamos de ver, tienen un número contable de discontinuidades del primer tipo, por lo tanto $f_1 \, – \, f_2 =f$ también cumple la condición.
Definición: Norma de $P.$ Sea $P=\{x_0=a , \, x_1, \, …, \, , x_n = b\}$ una partición de $[a,b].$ La norma de $P$ se define como la longitud del intervalo más grande de la partición y se denota como:
$$|P| := \underset{1 \leq i \leq n}{\text{máx }} \{x_i \, – \, x_{i-1}\}.$$
El resultado que veremos a continuación muestra condiciones bajo las cuales, cuando los intervalos generados por la partición son chiquititos, es posible aproximarse mucho a la variación a través de sumas $S_P.$ Esto no siempre es así, recordemos el tercer ejemplo de la entrada anterior. ¿Puedes dar ejemplos de particiones $P$ donde $S_P[f;a,b]$ no se acerca a $V,$ aun siendo $|P|$ menor que cualquier $\delta >0 ?$ (Ver ejercicio en tarea moral).
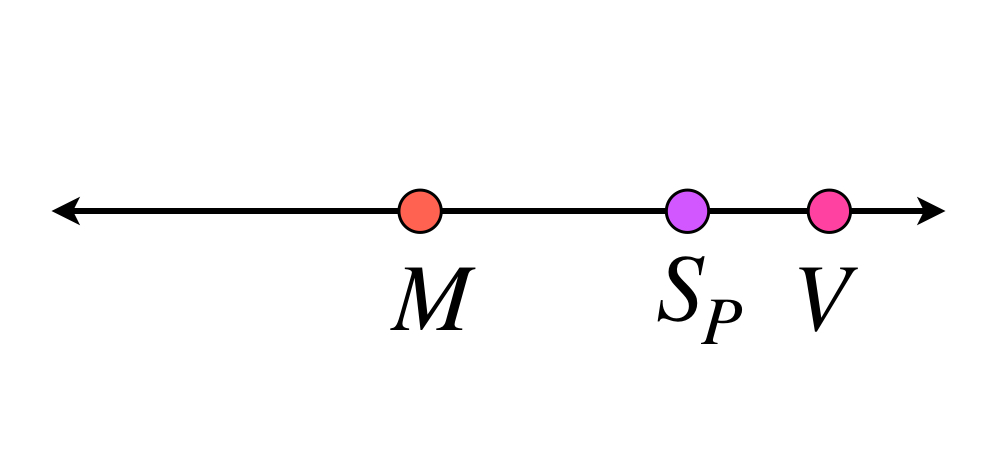
Proposición. Si $f$ es una función continua en $[a,b]$ entonces
$$V=\underset{|P| \to 0}{lim} \, S_P,$$
es decir, dado $M<V,$ existe $\delta >0$ tal que $M < S_P$ para cualquier partición $P$ de $[a,b]$ con $|P|< \delta.$
Demostración:
Tomemos
$$\hat{P} = \{\hat{x}_0=a,…,\hat{x}_n=b\}$$
tal que
\begin{align}
M+ \mu < S_{\hat{P}}.
\end{align}
Como $f$ es continua en $[a,b]$ entonces es uniformemente continua en $[a,b].$ Sea $\delta_1 >0$ tal que si $|x \, – \, x^*|< \delta_1$ entonces
\begin{align}
|f(x) \, – \, f(x^*)| < \frac{\mu}{2(n+1)}
\end{align}
Nota que $\frac{\mu}{2(n+1)}$ sí es fijo, pues $n$ lo es por ser el número de intervalos de la partición $\hat{P}$ elegida.
Toma $\delta >0$ tal que
\begin{align}
\delta < \text{mín} \{\delta_1, \underset{1 \leq i \leq n}{mín}\{\hat{x}_i \, – \, \hat{x}_{i-1}\}\}.
\end{align}
Sea $P=\{x_0, \, x_1, \, …, \, , x_m\}$ una partición de $[a,b],$ tal que $|P|< \delta.$ Afirmamos que esta partición satisface lo deseado, es decir que
\begin{align}
M < S_P.
\end{align}
Partimos de la igualdad
\begin{align}
S_P[f;a,b] = \sum_{i=1}^{m}|f(x_1) \, -\, f(x_{i-1})|
\end{align}
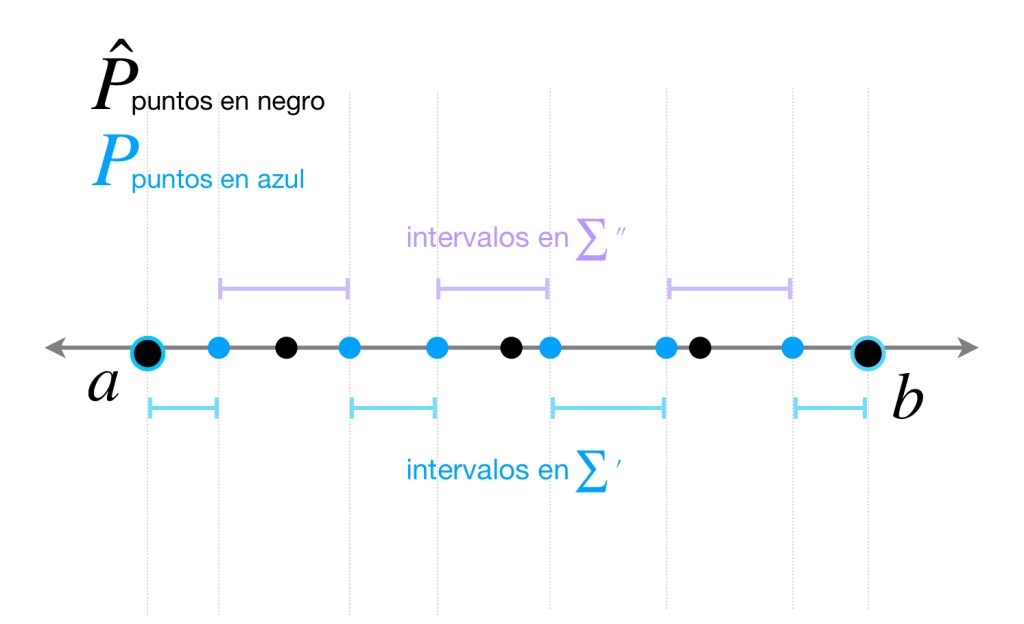
Ahora separemos los términos del lado derecho sumando en $\sum’$ todos los sumandos donde no hay elementos de $\hat{P}$ en el intervalo de $P$ correspondiente y sumando en $\sum ´´$ aquellos donde sí los hay.
\begin{align}
S_P[f;a,b] &= \sum_{i=1}^{m}|f(x_i) \, -\, f(x_{i-1})|
&= \sum’ + \sum ´´
\end{align}
Por (3) todos estos intervalos son menores que cualquier intervalo de $\hat{P},$ entonces cada intervalo $[x_{i-1}, x_i]$ de $P$ contiene a lo más un término $\hat{x}_j$ de $\hat{P}$ y así $\sum ´´$ tiene a lo más $n+1$ sumandos.
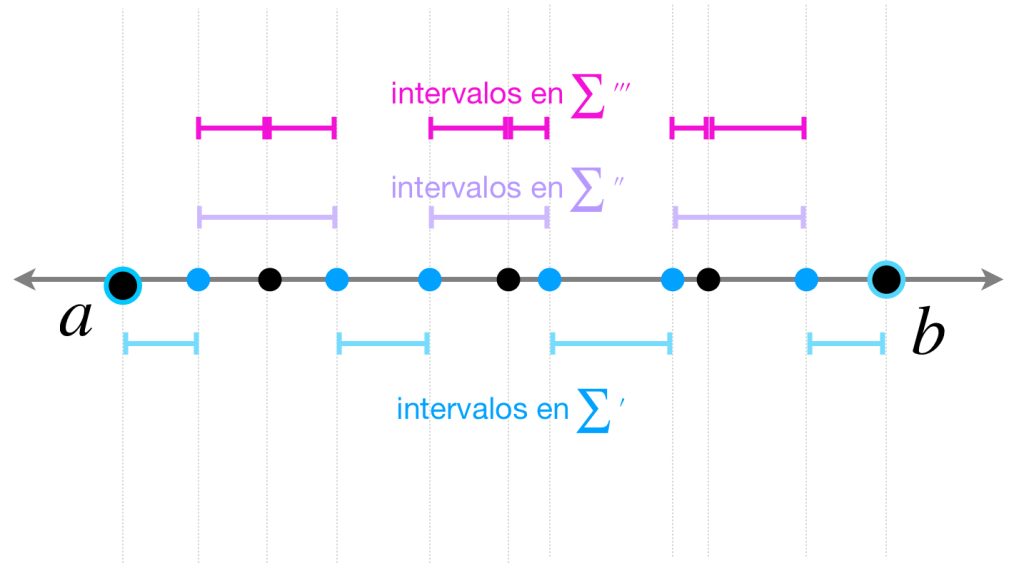
Sea $Q = P \cup \hat{P},$ entonces $Q$ es un refinamiento de ambas particiones. Bajo este indicador podemos reemplazar cada sumando de $\sum ´´$
$$|f(x_i) \, -\, f(x_{i-1})|$$
por los sumandos que separa el término $\hat{x}_j$ de $\hat{P}$
$$|f(x_i) \, -\, f(\hat{x}_{j})|+|f(\hat{x}_j) \, -\, f(x_{i-1})|.$$
La suma de todos estos la representaremos con $\sum´´´.$
Por (2) y (3),
\begin{align}
\sum´´´ < 2(n+1) \frac{\mu}{2(n+1)} = \mu.
\end{align}
y como
\begin{align}
S_Q = \sum’ + \sum´´´ \\
\Rightarrow \sum’ = S_Q \, – \, \sum´´´
\end{align}
de (7) y (8) tenemos
y como
\begin{align}
S_P > \sum’ > S_Q \, – \, \mu \geq S_{\hat{P}} – \mu > M
\end{align}
Por lo tanto $S_P > M$ que es lo que queríamos demostrar.
Corolario. Si $f$ tiene derivada continua $f’$ en $[a,b],$ se tiene que:
a) $V=\int_{a}^{b}|f'(x)|\, dx$
b) $S^+=\int_{a}^{b}(f'(x))^+ \, dx$
c) $S^-=\int_{a}^{b}(f'(x))^- \, dx$
Demostración:
a) Sea $P = \{x_0 =a,…,x_n =b\}$ una partición de $[a,b].$ Por el teorema del valor medio, aplicado en cada intervalo $[x_{i-1} \,, \, x_{i}]$ con $i = 1,…,n$ sabemos que existe $\xi_i \in [x_{i-1} , x_{i}]$ tal que
$$|f(x_i) \, – \, f(x_{i-1})| = |f'(\xi_i)|(x_i \, – \, x_{i-1})$$
Por el teorema que acabamos de demostrar concluimos que
\begin{align}
V = \underset{|P| \to 0}{lim} \, S_P = \underset{|P| \to 0}{lim} \, \sum_{i=1}^{n} |f'(\xi_i)|(x_i \, – \, x_{i-1}) = \int_{a}^{b} |f'(x)|\, dx.
\end{align}
b) A continuación usaremos un resultado visto en la entrada anterior y haremos también una sustitución en $V$ con la igualdad en a).
\begin{align}
\nonumber S^+ &= \frac{1}{2}(V \, + \, f(b) \, – \, f(a))\\
\nonumber &= \frac{1}{2}\left[\int_{a}^{b}|f'(x)|\, dx + \int_{a}^{b}f'(x) \, dx \right] \\
\nonumber &=\frac{1}{2} \int_{a}^{b} (|f'(x)|+f'(x)) \, dx \\
&= \int_{a}^{b} (f'(x))^+ \, dx.
\end{align}
c) La demostración es análoga a la anterior, partiendo de
$$S^- = \frac{1}{2}(V \, – \, f(b) \, + \, f(a))$$
y la proponemos como ejercicio.
Pasemos ahora a conocer las curvas rectificables, comenzando con aquellas que pertenecen al plano $\mathbb{R}^2.$
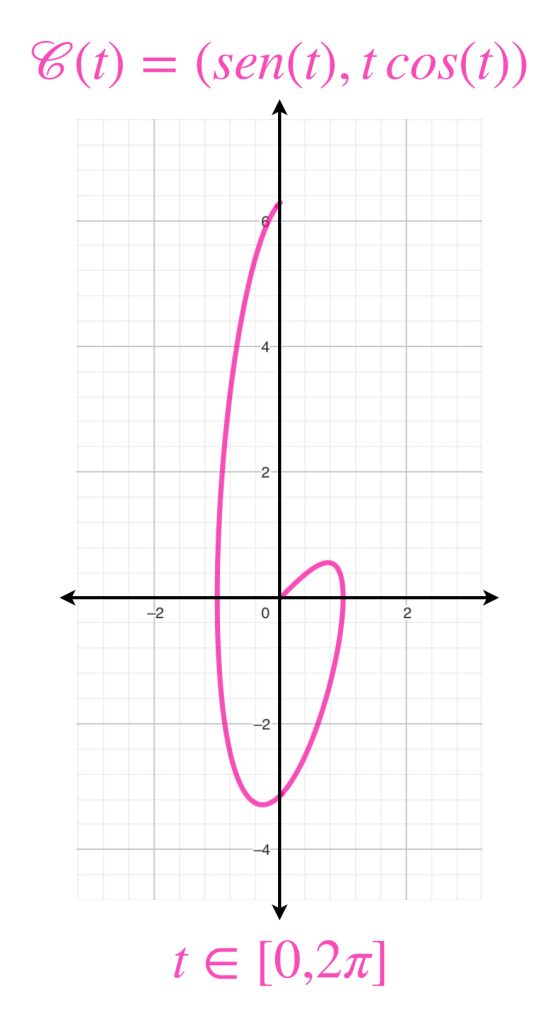
Definición. Curva en el plano y traza. Sean $\phi: [a,b] \to \mathbb{R}$ y $\psi: [a,b] \to \mathbb{R}$ dos ecuaciones paramétricas. Una curva en el plano $\mathbb{R}^2$ está dada por:
$\mathcal{C}(t)=(\phi(t), \, \psi(t))$ con $a \leq t \leq b.$
La traza de $\mathcal{C}$ es el conjunto $\{(x,y) \in \mathbb{R}^2 : x=\phi(t), \, y=\psi(t), \, a \leq t \leq b \}$.
Nota que en la definición no se excluye que la traza pueda tener intersecciones ni tampoco se dan las condiciones necesarias para que sea continua o acotada.
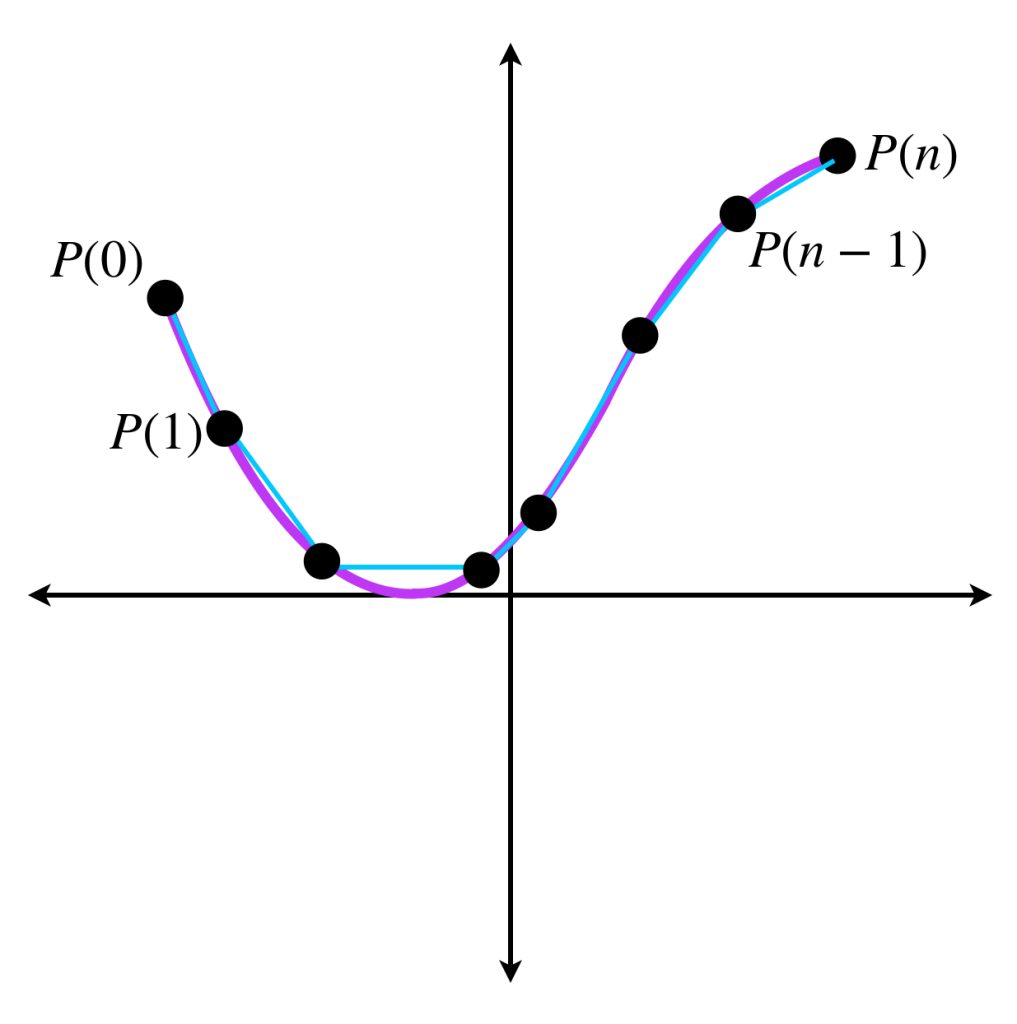
Definición. La longitud de $\mathcal{C}.$ Sea $P=\{t_0 =a, \, t_1,…,t_{n-1}, \, t_n= b\}$ una partición de $[a,b].$ Para cada $t_i, \, i= 0,…, n$ definimos $P_i := (\phi(x_i), \psi(x_i)).$ Pensemos en dibujar los puntos $P_i$ y las líneas que los conectan con su sucesor. La suma de la medida de cada una de estas líneas está dada por:
$$l(P)= \sum_{i=1}^{n} \, \sqrt{(\phi(t_i)-\phi(t_{i-1}))^2+(\psi(t_i)-\psi(t_{i-1}))^2}$$
y denota la longitud de la poligonal generada. Como esta longitud depende de la partición, presentamos la longitud de $\mathcal{C}$ como:
$$L=L(\mathcal{C})= \underset{P \in \mathcal{P}}{Sup} \, \, l(P)$$
Entonces $0 \leq L \leq \infty.$
Veamos bajo qué condiciones podemos hablar de una longitud finita.
Definición curva rectificable. Sea $\mathcal{C}$ una curva. Diremos que es rectificable si $L(\mathcal{C}) < \infty.$
Proposición. Sea $\mathcal{C}$ una curva. Entonces $\mathcal{C}$ es rectificable si y solo si tanto $\phi$ como $\psi$ son de variación acotada. Más aun.
$$V(\phi), \, V(\psi) \leq L \leq V(\phi) + V(\psi).$$
Demostración:
Supongamos que $\mathcal{C}$ es rectificable. Sea $P=\{t_0 =a, \, t_1,…,t_{n-1}, \, t_n= b\}$ una partición de $[a,b].$
Sabemos que para cualesquiera $A,B \in \mathbb{R},$
\begin{align}
|A| &\leq \sqrt{A^2 + B^2} \, \text{ y} \\
|B| &\leq \sqrt{A^2 + B^2}
\end{align}
Por definición
$$l(P)= \sum_{i=1}^{n} \, \sqrt{(\phi(t_i)-\phi(t_{i-1}))^2+(\psi(t_i)-\psi(t_{i-1}))^2} \leq L.$$
Usando (13) y (14) en cada término de $l(P)$
\begin{align}
\nonumber && \sum_{i=1}^{n} \, |\phi(t_i)-\phi(t_{i-1})|&\leq \sum_{i=1}^{n} \, \sqrt{(\phi(t_i)-\phi(t_{i-1}))^2+(\psi(t_i)-\psi(t_{i-1}))^2} \leq L \\
&\Rightarrow& V(\phi) &\leq L
\end{align}
Análogamente
\begin{align}
V(\psi) &\leq L
\end{align}
Es decir, $V(\phi) $ y $V(\psi)$ son de variación acotada. Recíprocamente, partiendo de este hecho y usando que para cualesquiera $A,B \in \mathbb{R}$ se cumple que
\begin{align}
\sqrt{A^2+B^2} \leq |A|+|B|
\end{align}
concluimos
\begin{align}
l(P) \leq \sum_{i=1}^{n} \, |\phi(t_i)-\phi(t_{i-1})|+\sum_{i=1}^{n} \, |\psi(t_i)-\psi(t_{i-1})| \leq V(\phi) + V(\psi)
\end{align}
Por lo tanto $L \leq V(\phi) + V(\psi)$ lo que significa que $\mathcal{C}$ es rectificable.
Al final de esta sección se te propone, en el ejercicio 4 de la tarea moral, una función que no es de variación acotada. De acuerdo con la proposición que acabamos de probar, la curva dada por $(f(t),f(t)), \, [0 \leq t \leq 1]$ no es rectificable aunque, curiosamente, tiene su traza en apenas un segmento de la línea $y =x$ en $\mathbb{R},$ lo que significa que la longitud de la traza de una curva no necesariamente coincide con la longitud de la curva.
Las curvas en $\mathbb{R}^n$
La idea de la curva en $\mathbb{R}^2$ también puede generalizarse en el caso $\mathbb{R}^n.$ A partir de $P=\{t_0 =a, \, t_1,…,t_{n-1}, \, t_m= b\}$ una partición de $[a,b]$ podemos definir la curva con puntos en $\mathbb{R}^n$ de la forma $(\phi_1(t), \, \phi_2(t),…, \phi_n(t))$ con $t \in [a,b]$ y donde cada $\phi_i$ es una ecuación paramétrica. La longitud de la curva está dada por:
$$l(P)= \sum_{i=1}^{m} \sqrt{ \sum_{j=1}^{n}(\phi_j(t_i) \, – \, \phi_j(t_i))^2 }.$$
También diremos que $L = \underset{P \in \mathcal{P}}{Sup} \, \, l(P)$ y si $L \in \mathbb{R}$ definimos que la curva es rectificable.
Más adelante…
Presentaremos la integral de Riemann-Stieltjes motivándola con conceptos de Probabilidad, viendo su significado a través de la función distribución o la esperanza.
Tarea moral
- Construye una función $f: \mathbb{R} \to \mathbb{R}$ no decreciente, acotada que sea continua en los números irracionales y discontinua en los racionales como sigue: si $\{r_n : n \in \mathbb{N}\}$ es el conjunto de números racionales define $f(x) = \underset{n \, : \, r_n \leq x}{\sum} \, 2^{-n}.$ ¿Es de variación acotada?
- El ejercicio 3 de la entrada anterior decía lo siguiente:
Sea $[a,b]$ un intervalo con el $\, 0$ en su interior y $f:[a,b] \to \mathbb{R}$ tal que
\begin{equation*}
f(x) = \begin{cases}
1 & \text{si $x = 0$} \\
0 & \text{si $x \neq 0$}
\end{cases}
\end{equation*}
Entonces $S_P = 2 \,$ o $\, S_P = 0,$ de modo que $V=2.$
Sea $\varepsilon>0.$ Para cada $\delta >0$ ¿Puedes dar ejemplo de una partición $P_{\delta} \,$ donde $|S_{P_{\delta}} \, – \, V|> \varepsilon, \,$ aun siendo $|P_{\delta}|$ menor que $\delta ?$ - Prueba que si $f$ tiene derivada continua, entonces $S^-=\int_{a}^{b}(f'(x))^- \, dx.$
- Sea $f:[0,1] \to \mathbb{R}$ tal que
\begin{equation*}
f(x)=\begin{cases}
x \, sen(\frac{1}{x}), \, \text{ si $0<x \leq 1$} \\
f(x) = 0, \, \text{ si $x=0$}
\end{cases}
\end{equation*}
Muestra que $f$ es acotada y continua en $[0,1]$ pero $V = \infty.$ - Demuestra que también en el caso en que la curva está en $\mathbb{R}^n,$ $\mathbb{C}$ es rectificable si y solo si cada $\phi_j$ es de variación acotada.