Introducción

En esta entrada veremos varios ejemplos relacionados con el teorema de Fubini.

La condición de integrabilidad es necesaria en el Teorema de Fubini

En general, no podemos relajar las hipótesis de positividad o integrabilidad en el Teorema de Fubini. Veamos un ejemplo concreto.

Ejemplo. Consideremos $Q=(0,\infty)\times(0,\infty) $. Definamos $R\subseteq Q$ como la región acotada por las rectas $y=x$ y $y=x-1$, y $S\subseteq Q$ la región acotada por las rectas $y=x-1$, $y=x-2$ como se observa en la figura. Claramente $\lambda(R),\lambda(S)=\infty$.

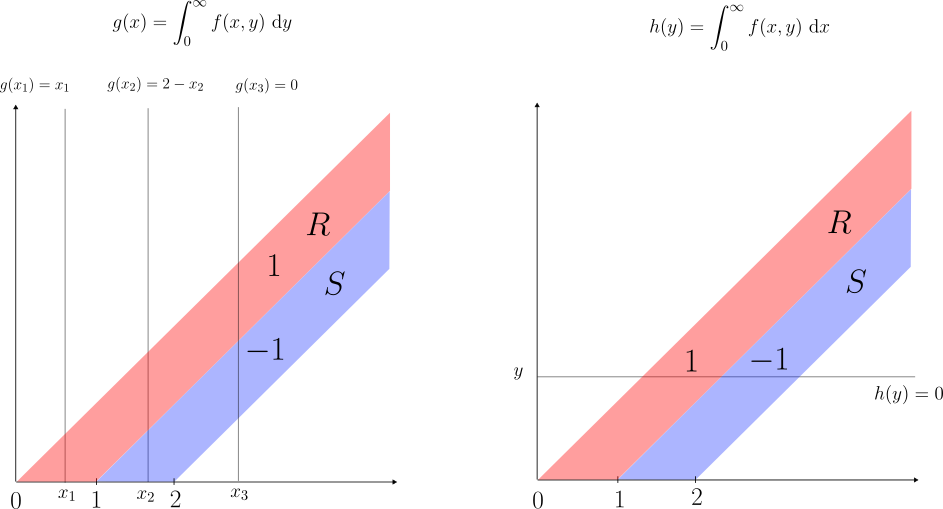
Sea $f=\chi_R-\chi_S$. Ésta NO es una función integrable pues $f_+=\chi_R$ $\implies$ $\int f_+ \ \mathrm{d}\lambda=\int \chi_R \ \mathrm{d}\lambda=\infty$ y de manera similar $f_-=\chi_S$ $\implies$ $\int f_- \ \mathrm{d}\lambda=\int \chi_S \ \mathrm{d}\lambda=\infty$.

Ahora, para cada $x\geq 0$ consideremos la función: $$g(x)=\int_{0}^{\infty}f(x,y) \ \mathrm{d}y.$$ Es fácil ver que:

\begin{equation*}
g(x)=
\begin{cases}
x & \text{si } 0\leq x \leq 1 \\
2-x & \text{si } 1\leq x \leq 2 \\
0 & \text{si } 2\leq x
\end{cases}
\end{equation*}

Así que $g$ es claramente medible. Además:

$$\int_0^\infty g(x) \ \mathrm{d}x=\int_0^1 x \ \mathrm{d}x+\int_1^2 (2-x) \ \mathrm{d}x=\frac{1}{2}+\frac{1}{2}=1.$$

Por otro lado, consideremos:
$$h(y)=\int_{0}^{\infty}f(x,y) \ \mathrm{d}x.$$ Es fácil ver que en $(0,\infty)$: $$h\equiv 0 \ \implies \int_0^\infty h(y) \ \mathrm{d}y =0.$$

Es decir: $$\int_0^\infty \left( \int_0^\infty f(x,y) \ \mathrm{d}y \right) \mathrm{d}x=1\neq 0=\int_0^\infty \left( \int_0^\infty f(x,y) \ \mathrm{d}x \right) \mathrm{d}y.$$
De modo que las integrales iteradas ni siquiera coinciden.

$\triangle$

Algunos ejercicios resueltos

Veamos ahora algunos ejercicios resueltos, un poco más sofisticados, en los que el teorema de Fubini juega un papel fundamental.

Ejercicio. Calcular $$\int_R 2x^2+4xy+2x+2y^2-2y \ \mathrm{d}x\mathrm{d}y.$$ Donde $R$ es el conjunto de puntos $(x,y)\in \mathbb{R}^2$ tales que $|x|+|y|\leq 1$.

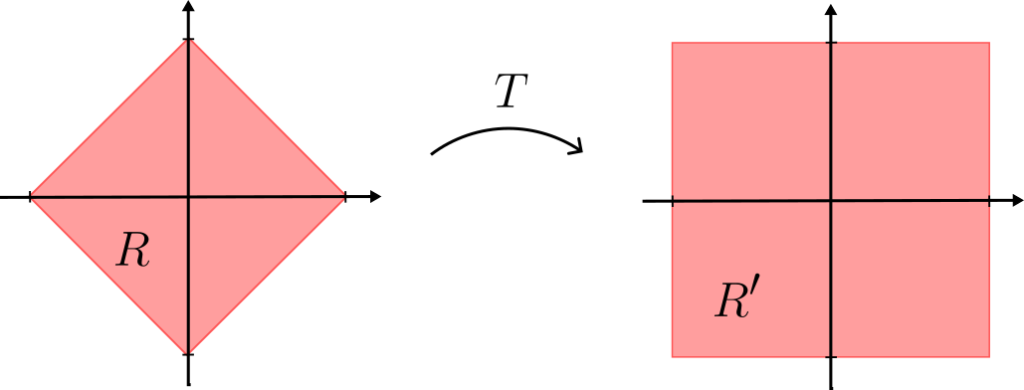
Solución. La región $R$ es un rombo con vértices $(1,0),(0,1),(-1,0),(0,-1)$, que no es un producto de conjuntos, así que no podemos usar el teorema de Fubini directamente.

Conviene entonces transformar la región de integración a una región en la que sea más sencillo aplicar el teorema de Fubini. Lo más natural es hacer un cambio de variable con una rotación de $\pm \frac{\pi}{4}$, pues de esta manera $R$ se transforma en un rectángulo, aunque por simplicidad algebráica proponemos : $$u=x+y; \ \ \ \ \ v=x-y.$$ O equivalentemente \begin{equation*}\begin{pmatrix}
u \\
v
\end{pmatrix} = \begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix} \begin{pmatrix}
x \\
y
\end{pmatrix}=T\begin{pmatrix}
x\\
y
\end{pmatrix}. \end{equation*}

Geométricamente $T$ es una rotación con ángulo $-\frac{\pi}{4}$, compuesta con una reflexión y una dilatación. Mediante este cambio, $R$ se transforma en un rectángulo $R’$ con vértices $(1,1),(1,-1),(-1,-1),(-1,1)$, es decir $R’=[-1,1]\times[-1,1]$.

Como $|\det T|=2$, se sigue por el teorema de cambio de variable y el teorema de Fubini:

\begin{align*}
\int_R 2x^2+4xy+2x+2y^2-2y \ \mathrm{d}x\mathrm{d}y &= 2\int_R (x+y)^2+(x-y) \ \mathrm{d}x\mathrm{d}y \\
&= \int_{R’} u^2+v \ \mathrm{d}u\mathrm{d}v \\
&= \int_{-1}^{1} \int_{-1}^{1} u^2+v \ \mathrm{d}u\mathrm{d}v \\
&= \int_{-1}^{1} \left[\frac{u^3}{3}\right]_{u=-1}^{u=1}+(1-(-1))v \ \mathrm{d}v \\
&= \int_{-1}^1 \frac{2}{3}+2v \ \mathrm{d}v \\
&= (1-(-1))\frac{2}{3}+2\left[\frac{v^2}{2} \right]_{v=-1}^{v=1} \\
&= \frac{4}{3}.
\end{align*}

$\triangle$

Ejercicio (Integral Gaussiana). Demuestra que $$\int_{\mathbb{R}^n} e^{-|x|^2} \ \mathrm{d}x=\pi^{\frac{n}{2}}. $$

Solución. Veamos primero el caso $n=1$: $\int_{\mathbb{R}} e^{-x^2} \ \mathrm{d}x=\sqrt{\pi} $. Notemos que la función $f(x)= e^{-x^2}$ es una función par (i.e. $f(x)=f(-x)$ $\forall x\in \mathbb{R}$) y no negativa. Haciendo el cambio de variable $y=-x$, es fácil ver que $\int_{-\infty}^{0} e^{-x^2} \ \mathrm{d}x=\int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x$, de donde $\int_{-\infty}^{\infty} e^{-x^2} \ \mathrm{d}x=2\int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x$, así que basta probar que $$\int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x=\frac{\sqrt{\pi}}{2}.$$

Para esto, calculemos $$I=\int_{(0,\infty)\times(0,\infty)} xe^{-x^2(1+y^2)} \ \mathrm{d}x\mathrm{d}y.$$ De dos formas distintas usando el teorema de Fubini. Por un lado:

\begin{align*}
I &= \int_{0}^{\infty} \int_{0}^{\infty} xe^{-x^2(1+y^2)} \ \mathrm{d}x \ \mathrm{d}y \\
&= \int_{0}^{\infty} \int_{0}^{\infty} \frac{-1}{2(1+y^2)} \left( -2x(1+y^2)e^{-x^2(1+y^2)} \right) \ \mathrm{d}x \ \mathrm{d}y \\
&= \int_{0}^{\infty} \frac{-1}{2(1+y^2)} \int_{0}^{\infty} \frac{\mathrm{d}}{\mathrm{d}x} \left( e^{-x^2(1+y^2)} \right) \ \mathrm{d}x \ \mathrm{d}y \\
&= \int_{0}^{\infty} \frac{-1}{2(1+y^2)} \left( \left[ e^{-x^2(1+y^2)} \right]_{x=0}^{x=\infty} \right) \ \mathrm{d}y \\ &= \int_{0}^{\infty} \frac{-1}{2(1+y^2)} \left( 0 – 1 \right) \ \mathrm{d}y \\
&= \int_{0}^{\infty} \frac{1}{2(1+y^2)} \ \mathrm{d}y \\
&= \frac{1}{2} \int_{0}^{\infty} \frac{\mathrm{d}}{\mathrm{d}y}\left( \arctan(y) \right) \ \mathrm{d}y \\
&= \frac{1}{2} \left[ \arctan(y) \right]_{y=0}^{y=\infty} \\
&= \frac{1}{2}[\frac{\pi}{2}-0] \\
&= \frac{\pi}{4}
\end{align*}

En la segunda igualdad multiplicamos y dividimos por $-2(1+y^2)$ para poder escribir el integrando como una derivada. En las demás, hacemos uso del teorema fundamental del cálculo, convergencia monótona y tomamos límites (ya hemos hecho este argumento varias veces así que omitimos los detalles).

Por otro lado:

\begin{align*}
I &= \int_{0}^{\infty} \int_{0}^{\infty} xe^{-x^2}e^{-x^2y^2} \ \mathrm{d}y \ \mathrm{d}x \\
&= \int_{0}^{\infty} xe^{-x^2} \int_{0}^{\infty} e^{-x^2y^2} \ \mathrm{d}y \ \mathrm{d}x \\
\end{align*}

Haciendo el cambio de variable: $z=xy$ en la integral de en medio:

\begin{align*}
&= \int_{0}^{\infty} xe^{-x^2} \int_{0}^{\infty} \frac{1}{x} e^{-z^2} \ \mathrm{d}z \ \mathrm{d}x \\
&= \int_{0}^{\infty} e^{-x^2} \int_{0}^{\infty} e^{-z^2} \ \mathrm{d}z \ \mathrm{d}x \\
&= \left( \int_{0}^{\infty} e^{-z^2} \ \mathrm{d}z \right) \left( \int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x \right) \\
&= \left( \int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x \right)^2
\end{align*}

$$\implies I=\left( \int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x \right)^2=\frac{\pi}{4}$$ $$\implies \int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x = \frac{\sqrt{\pi}}{2}.$$

Esto completa el caso $n=1$. Ahora, para el caso general, simplemente notemos que:

\begin{align*}
\int_{\mathbb{R}^n} e^{-|x|^2} \ \mathrm{d}x &= \int_{\mathbb{R}} \int_{\mathbb{R}} \dots \int_{\mathbb{R}} e^{-x_1^2}e^{-x_2^2}\dots e^{-x_n^2} \ \mathrm{d}x_n \dots \mathrm{d}x_2 \mathrm{d}x_1 \\
&= \int_{\mathbb{R}} e^{-x_1^2}\left( \int_{\mathbb{R}} e^{-x_2^2} \left( \dots \int_{\mathbb{R}} e^{-x_n^2} \ \mathrm{d}x_n \dots \right) \mathrm{d}x_2 \right) \mathrm{d}x_1 \\
&= \left( \int_{\mathbb{R}} e^{-x_1^2} \ \mathrm{d}x_1 \right)\left( \int_{\mathbb{R}} e^{-x_2^2} \ \mathrm{d}x_2 \right)\dots \left( \int_{\mathbb{R}} e^{-x_n^2} \ \mathrm{d}x_n \right) \\
&= \left( \int_{\mathbb{R}} e^{-y^2} \ \mathrm{d}y \right)^n \\
&= \left( \sqrt{\pi} \right)^n \\
&= \pi^{\frac{n}{2}}.
\end{align*}

$\triangle$

Ejercicio. Sean $a_1,a_2,\dots,a_n>0$. Sea $J=(0,1)\times(0,1)\times \dots \times(0,1)$. Demuestra que $$\int_J\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}} \ \mathrm{d}x<\infty \ \iff \ \sum_{i=1}^{n}\frac{1}{a_i}>1.$$

Antes de proceder, usaremos un lema sencillo, consecuencia del teorema fundamental del cálculo. Omitimos la demostración.

Lema. $\int_0^1 y^{s-1} \ \mathrm{d}y<\infty$ $\iff$ $s>0$.

Solución. Para cada $1\leq i \leq n$, consideremos $G_i= \{ x\in J \ | \ x_j^{a_j}\leq x_i^{a_i} $ para todo $ j \}$. Claramente $J=\bigcup_{i=1}^{n}G_i$. Además, para $x\in G_i$ se cumple $x_i^{a_i}\leq x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}\leq n x_i^{a_i}$. Esto nos garantiza que:
$$\int_{G_i}\frac{1}{nx_1^{a_1}} \ \mathrm{d}x\leq \int_{G_i}\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}} \ \mathrm{d}x \leq \int_J\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}} \ \mathrm{d}x.$$ Y de manera similar:
$$ \int_J\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}} \ \mathrm{d}x\leq \sum_{i=1}^{n}\int_{G_i}\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}} \ \mathrm{d}x\leq \sum_{i=1}^{n}\int_{G_i}\frac{1}{x_i^{a_i}} \ \mathrm{d}x.$$

Ahora, para cada $i=1,\dots,n$ podemos escribir:

$$\int_{G_i}\frac{1}{x_i^{a_i}} \ \mathrm{d}x=\int_0^1 \left( \int_0^1 \dots \int_0^1 \frac{1}{x_i^{a_i}} \chi_{G_i}(x_1\dots,x_n) \ \mathrm{d}x_1\dots \mathrm{d}x_{i-1}\mathrm{d}x_{i+1}\dots \mathrm{d}x_n \right) \mathrm{d}x_i.$$

Para $x_i\in (0,1)$ fijo, en la integral de en medio, $x_1$ varía entre $0$ y $x_i^{\frac{a_i}{a_1}}$; $x_2$ varía entre $0$ y $x_i^{\frac{a_i}{a_2}}$, etc. De manera que la integral se puede reescribir como:

$$\int_0^1 \left( \int_0^{x_i^{\frac{a_i}{a_1}}}\dots \int_0^{x_i^{\frac{a_i}{a_{i-1}}}} \int_0^{x_i^{\frac{a_i}{a_{i+1}}}}\dots \int_0^{x_i^{\frac{a_i}{a_{n}}}} \frac{1}{x_i^{a_i}} \ \mathrm{d}x_1\dots \mathrm{d}x_{i-1}\mathrm{d}x_{i+1}\dots \mathrm{d}x_n \right) \mathrm{d}x_i $$

$$=\int_0^1 \frac{1}{x_i^{a_i}} \left( \int_0^{x_i^{\frac{a_i}{a_1}}}\dots \int_0^{x_i^{\frac{a_i}{a_{i-1}}}} \int_0^{x_i^{\frac{a_i}{a_{i+1}}}}\dots \int_0^{x_i^{\frac{a_i}{a_{n}}}} 1 \ \mathrm{d}x_1\dots \mathrm{d}x_{i-1}\mathrm{d}x_{i+1}\dots \mathrm{d}x_n \right) \mathrm{d}x_i $$
$$ =\int_0^1 \frac{1}{x_i^{a_i}} \left( x_i^{\frac{a_i}{a_1}} \right) \dots \left( x_i^{\frac{a_i}{a_{i-1}}} \right)\left( x_i^{\frac{a_i}{a_{i+1}}} \right)\dots \left( x_i^{\frac{a_i}{a_n}} \right) \ \mathrm{d}x_i$$
$$ =\int_0^1 x_i^{a_i\left( \sum_{j=1}^n\frac{1}{a_j}-1 \right)-1} \ \mathrm{d}x_i.$$

Por tanto, los estimados anteriores se pueden reescribir como:

$$\frac{1}{n} \int_0^1 x_1^{a_1\left( \sum_{j=1}^n\frac{1}{a_j}-1 \right)-1} \ \mathrm{d}x_1 \leq \int_J \frac{1}{x_1^{a_1}+\dots+x_n^{a_n}} \ \mathrm{d}x\leq \sum_{i=1}^{n}\int_0^1 x_i^{a_i\left( \sum_{j=1}^n\frac{1}{a_j}-1 \right)-1} \ \mathrm{d}x_i.$$

Se sigue entonces del Lema que $\int_J \frac{1}{x_1^{a_1}+\dots+x_n^{a_n}} \ \mathrm{d}x<\infty$ $\iff$ $\sum_{j=1}^n\frac{1}{a_j}-1>0$ $\iff$ $\sum_{j=1}^n\frac{1}{a_j}>1$.

$\triangle$

Más adelante…

Daremos finalmente una prueba del Teorema de Fubini-Tonelli.

Tarea moral

• Sea $R$ la región delimitada por las rectas $x+y=0$, $x+y=2$, $2x-y=0$ y $2x-y=3$. Calcula $$\int (2x+y) \ \mathrm{d}x\mathrm{d}y .$$ [SUGERENCIA: Utiliza el cambio de variable $u=x+y$, $v=2x-y$].
• Sea $D=\{ (x,y)\in \mathbb{R}^2 \ | \ 0 \leq x \leq y \leq 1 \}.$ Calcula $$\int_D \frac{y}{x^2+y^2} \ \mathrm{d}x\mathrm{d}y.$$
• Sean $a,b>0$. Prueba que $$\int_{0}^{\infty}\frac{e^{-ax}-e^{-bx}}{x} \ \mathrm{d}x=\log \frac{b}{a}.$$ [SUGERENCIA: Calcula de dos maneras la integral de $e^{-xy}$ sobre la franja $[0,\infty]\times [a,b]$].
• (Convoluciones). La convolución de dos funciones $f,g:\mathbb{R}^n\to [-\infty,\infty]$ se define (cuando sea posible) como la función: $$(f*g)(x)=\int_{\mathbb{R}^n} f(x-y)g(y) \ \mathrm{d}y. $$
  • Prueba que si $f$ y $g$ son medibles sobre $\mathbb{R}^n$, entonces la función $f(x-y)g(y)$ es medible sobre $\mathbb{R}^{2n}$.
  • Prueba que si $f,g\in L^1(\mathbb{R}^n)$, entonces $f(x-y)g(y)$ es integrable sobre $\mathbb{R}^{2n}$.
  • Prueba que si $f$ y $g$ son integrables, entonces la convolución está definida en casi todo punto y $(f*g)\in L^1(\mathbb{R}^n)$ con $$\int |f*g| \ \mathrm{d}\lambda\leq \left( \int |f| \ \mathrm{d}\lambda \right) \left( \int |g| \ \mathrm{d}\lambda \right) .$$
  • Si $f,g,h\in L^1(\mathbb{R}^n)$, demuestra que $$f*g=g*f$$ Y $$(f*g)*h=f*(g*h).$$ En casi todo punto.
• (Continuación del último ejercicio). Usaremos la notación del último ejercicio resuelto.
  • Definamos $J’=((0,\infty)\times \dots \times (0,\infty))\setminus J$. Prueba que $$\int_{J’}\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots + x_n^{a_n}}<\infty \ \ \ \iff \ \ \ \sum_{i=1}^{n}\frac{1}{a_i}<1.$$ [SUGERENCIA: Imita la solución del último ejercicio resuelto].
  • Demuestra que existen constantes $c_1,c_2>0$ (que dependen solamente de $n$ y $a>0$) tales que para todo $x=(x_1,\dots,x_n)\in \mathbb{R}^n$: $$c_1(|x_1|^a+\dots+|x_n|^a)\leq \|x\|^a\leq c_2 (|x_1|^a+\dots+ |x_n|^a).$$ (Abusando de la notación, $|x|$ denota la norma usual en $\mathbb{R}^n$ y $|x_k|$ la norma en $\mathbb{R}$). [SUGERENCIA: Por compacidad, la función $f(x)=\frac{\sum_{i=1}^{n}|x_i|^a}{|x|}$ alcanza un máximo y un mínimo sobre la esfera unitaria $S_{n-1}= \{x \ | \ |x|=1 \}$].
  • Utiliza los incisos anteriores para probar que $$\int_{B_1(0)}\frac{1}{|x|^a} \ \mathrm{d}x < \infty \ \ \ \iff \ \ \ a<n;$$ $$\int_{B_1(0)^c}\frac{1}{|x|^a} \ \mathrm{d}x < \infty \ \ \ \iff \ \ \ a>n.$$