Introducción
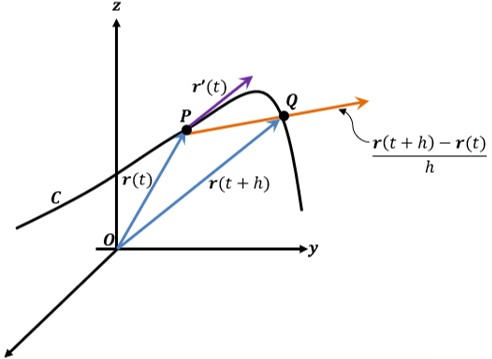
Generalizando un poco las ideas del cálculo diferencial de funciones $f:\mathbb{R}\rightarrow \mathbb{R}$ a funciones $f:\mathbb{R}\rightarrow \mathbb{R}^{n}$. Recordemos que $f:\mathbb{R}\rightarrow \mathbb{R}$ es diferenciable en un punto $t_{0}$ si
$$\lim_{h\rightarrow 0}\frac{f(t_{0}+h)-f(t_{0})}{h}$$existe y en tal caso lo denotamos $f'(t_{0})$
Definición. Sea $r:I\subset\mathbb{R}\rightarrow \mathbb{R}^{n}$ una función vectorial definida en un intervalo abierto $I\in\mathbb{R}$ y $t\in I$. Se define la derivada de f en $t$, denotada por $r'(t)$ como
$$r'(t)=\lim_{h\rightarrow 0}\frac{r(t+h)-r(t)}{h}$$cuando este limite existe
Ejemplo. Usa la definición para calcular la derivada de la función.
$$r(t)=(3t+4)i+(t^{2}-4t+3)j$$
Tenemos que
$$r'(t)=\lim_{h\rightarrow0}\frac{r(t+h)-r(t)}{h}$$
$$=\lim_{h\rightarrow0}\frac{[(3(t+h)+4)i+((t+h)^{2}-4(t+h)+3)j]-[(3t+4)i+(t^{2}-4t+3)j]}{h}$$
$$=\lim_{h\rightarrow0}\frac{(3t+3h+4)i-(3t+4)i+(t^{2}+2th+h^{2}-4t-4h+3)j-(t^{2}-4t+3)j}{h}$$
$$=\lim_{h\rightarrow0}(3i+(2th+h-4)j)$$
$$=3i+(2t-4)j.~~ \blacksquare$$
Teorema. Sea $f:\mathbb{R} \rightarrow \mathbb{R}^{n}$ una función vectorial, $t_{0}\in \mathbb{R}$. f es diferenciable en el punto $t_{0}$ si y solo si cada función componente $x_{i}(t)$ de f es diferenciable en el punto $t_{0}$, en cuyo caso $$f'(t_{0})=(x’_{1}(t_{0}),x’_{2}(t_{0}),..,x’_{n}(t_{0}))$$
Demostración. $(\textcolor{red}{\Rightarrow})$
Supongamos que f es diferenciable en $t_{0}$. Entonces
$$\lim_{h\rightarrow 0}\frac{f(t_{0}+h)-f(t_{0})}{h}$$
Por otro lado
$$\lim_{h\rightarrow 0}\frac{f(t_{0}+h)-f(t_{0})}{h}=\lim_{h\rightarrow 0}\left(\frac{(x_{1}(t_{0}+h),x_{2}(t_{0}+h),…,x_{n}(t_{0}+h))-(x_{1}(t_{0}),x_{2}(t_{0}),…,x_{n}(t_{0}))}{h}\right)$$
$$=\lim_{h\rightarrow 0}\left(\frac{x_{1}(t_{0}+h)-x_{1}(t_{0})}{h},\frac{x_{2}(t_{0}+h)-x_{2}(t_{0})}{h},…,\frac{x_{n}(t_{0}+h)-x_{n}(t_{0})}{h}\right)$$
$$=\left(\lim_{h\rightarrow 0}\frac{x_{1}(t_{0}+h)-x_{1}(t_{0})}{h},\lim_{h\rightarrow 0}\frac{x_{2}(t_{0}+h)-x_{2}(t_{0})}{h},…,\lim_{h\rightarrow 0}\frac{x_{n}(t_{0}+h)-x_{n}(t_{0})}{h}\right)$$
conforme $h\rightarrow 0$ cada limite de las funciónes componentes existe $\therefore$
$$\lim_{h\rightarrow 0}\frac{x_{i}(t_{0}+h)-x_{i}(t_{0})}{h}=x’_{i}(t_{0})$$
$\therefore$ cada $x_{i}$ es diferenciable en $t_{0}$
$(\textcolor{red}{\Leftarrow})$ Se pueden regresar en los pasos de la prueba anterior.$~~ \blacksquare$
Definición. La derivada $f'(t)$ de una trayectoria f puede ser asociada a una matriz $n\times 1$ la cual es conocida como la matriz Jacobiana de f en el punto $t_{0}$.
Se denota
$$Jf(t_{0})=\left[\begin{matrix}x’_{1}(t_{0})\\x’_{2}(t_{0})\\\vdots\\x’_{n}(t_{0})\end{matrix}\right]$$
Propiedades de la derivada de funciones con valores vectoriales
Ejercicio. Utiliza la definición de derivada para demostrar que:
Si $f:\mathbb{R}\rightarrow \mathbb{R}^{n}$ esta dada por $f(t)=a\in\mathbb{R}^{n}$, $a$ constante, entonces $f'(t)=0$
Solución.
$$f'(t)=\lim_{h \rightarrow 0}\frac{f(t+h) – f(t)}{h}=
\lim_{h \rightarrow 0} \frac{a-a}{h} = 0.~~ \blacksquare$$
Ejercicio. Prueba lo siguiente: Si $f(t)=ah(t)$ entonces $f'(t)=ah'(t)$
Solución.
\[\begin{array}{ll}
f'(t) & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h) – f(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{ah(t+h t) – ah(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0} a \lim_{h \rightarrow 0}\frac{h(t+h) – h(t)}{h}\\
\ \ & = ah'(t).~~ \blacksquare
\end{array}\]
Ejercicio. Demuestre lo siguiente: Si $f(t)$ y $g(t)$ son funciones
vectoriales, entonces $(f+g)'(t)=f'(t)+g'(t)$
Solución
\[\begin{array}{ll}
(f+g)'(t) & = \displaystyle\lim_{h \rightarrow 0}\frac{f+g(t+h) – [f+g(t)]}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)+g(t+h) – f(t)-g(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h) – f(t)}{h} + \frac{g(t+h) – g(t)}{h}\\
\ \ & = f'(t)+g'(t).~~ \blacksquare
\end{array}\]
Ejercicio. Pruebe lo siguiente: $(f\cdot g)'(t)=f(t)\cdot g'(t)+f'(t)\cdot g(t)$
Solución.
\[\begin{array}{ll}
(f\cdot g(t))’& = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\cdot g(t+h) – f(t)\cdot g(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\cdot[g(t+h) – g(t)] +[f(t+h)-f(t)]\cdot g(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\cdot[g(t+h) – g(t)]}{h} + \frac{[f(t+h) – f(t)]\cdot g(t)}{h}\\
\ \ & = f(t)\cdot g'(t)+f'(t)\cdot g(t).~ \blacksquare
\end{array}\]
$\fbox{$(f \times g)'(t)=f(t)\times g'(t)+f'(t)\times g(t)$}$
Solución.
\[\begin{array}{ll}
(f\times g(t))’& = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\times g(t+h) – f(t)\times g(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\times [g(t+h) – g(t)] +[f(t+h)-f(t)]\times g(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\times [g(t+h) – g(t)]}{h} + \frac{[f(t+h) – f(t)]\times g(t)}{h}\\
\ \ & = f(t)\times g'(t)+f'(t)\times g(t).~~ \blacksquare
\end{array}\]
Ejemplo. Dadas las funciones vectoriales
\begin{align*}
r(t)&=(6t+8)i+(4t^{2}+2t-3)j+5tk\\
u(t&)=(t^{2}-3)i+(2t+4)j+(t^{3}-3t)k
\end{align*}
calcule cada una de las siguientes derivadas usando las propiedades de la derivada de funciones vectoriales.
$$\displaystyle{\frac{d}{dt}[r(t)\cdot u(t)]}$$
$$\displaystyle{\frac{d}{dt}[u(t)\times u'(t)]}$$
En este caso tenemos que $r'(t)=6i+(8t+2)j+5k$ y $u'(t)=2ti+2j+(3t^{2}-3)k$. Por tanto
\begin{align*} \frac{d}{dt}[r(t)\cdot u(t)]&=r'(t)\cdot u(t)+r(t)\cdot u'(t) \\ &=(6i+(8t+2)j+5k)\cdot((t^{2}-3)i+(2t+4)j+(t^{3}-3t)k) \\ &+((6t+8)i+(4t^{2}+2t-3)j+5tk)\cdot(2ti+2j+(3t^{2}-3)k) \\ &=6(t^{2}-3)+(8t+2)(2t+4)+5(t^{3}-3t) \\ &+2t(6t+8)+2(4t^{2}+2t-3)+5t(3t^{2}-3) \\ &=20t^{3}+42t^{2}+26t-16. \end{align*}
Primero, necesitamos adaptar la propiedad correspondiente para este problema:
$$\frac{d}{dt}[u(t)\times u'(t)]=u'(t)\times u'(t)+u(t)\times u^{\prime\prime}(t)$$
Recuerda que el producto cruz de cualquier vector consigo mismo es cero. Además, $u^{\prime\prime}(t)$ representa la segunda derivada de $u(t)$:
$$u^{\prime\prime}(t)=\frac{d}{dt}[u'(t)]=\frac{d}{t}[2ti+2j+(3t^{2}-3)k]=2i+6tk$$
Por lo tanto
\begin{align*} \frac{d}{dt}[u(t)\times u'(t)]&=0+((t^{2}-3)i+(2t+4)j+(t^{3}-3t)k)\times (2i+6tk) \\ &=\left|\begin{matrix}i&j&k\\t^{2}-3&2t+4&t^{3}-3t\\2&0&6t\end{matrix}\right| \\ &=6t(2t+4)i-(6t(t^{2}-3)-2(t^{3}-3t))j-2(2t+4)k \\ &=(12t^{2}+24t)i+(12t-4t^{3})j-(4t+8)k.~ \blacksquare \end{align*}
Integrales de funciones con valores vectoriales
Introdujimos antiderivadas de funciones con valores reales en Antiderivadas e integrales definidas de funciones de valor real. Cada uno de estos conceptos se puede extender a funciones con valores vectoriales. Además, así como podemos calcular la derivada de un valor vectorial diferenciando las funciones componentes por separado, podemos calcular la antiderivada de la misma manera. Además, el Teorema Fundamental del Cálculo se aplica también a las funciones vectoriales. La antiderivada de una función vectorial aparece en las aplicaciones. Por ejemplo, si una función con valores vectoriales representa la velocidad de un objeto en el tiempo t, entonces su antiderivada representa la posición. O, si la función representa la aceleración del objeto en un momento dado, entonces la antiderivada representa su velocidad.
Sean $f_{1}(t),…,f_{n}(t)$ funciones de variable real sobre un intervalo $[a,b]$.
La integral indefinida de una función vectorial $r(t)=(f_{1}(t), \ldots,f_{n}(t))$ es
$$\boxed{\int~r(t)~dt=\int[(f_{1}(t), \ldots,f_{n}(t))]=\left[\int~f_{1}(t)~dt,~\int~f_{2}(t)~dt,…,\int~f_{n}(t)~dt\right]}$$
La integral definida de una función vectorial es
$$\boxed{\int_{a}^{b}~r(t)~dt=\int_{a}^{b}[(f_{1}(t), \ldots,f_{n}(t))]=\left[\int_{a}^{b}~f_{1}(t)~dt,~\int_{a}^{b}~f_{2}(t)~dt,…,\int_{a}^{b}~f_{n}(t)~dt\right]}$$
La integral existe siempre que cada una de las integrales $\displaystyle\int_{a}^{b}f_{i}(t)~dt$ con $i=1,\ldots,n$ existe. En particular, si $f_{i}$ es continua sobre $[a,b]$ entonces $\displaystyle\int_{a}^{b}f_{i}(t)~dt$ existe.
Dado que la integral indefinida de una función con valores vectoriales implica integrales indefinidas de las funciones componentes, cada una de estas integrales de componentes contienen una constante de integración. Todas pueden ser diferentes. Por ejemplo en el caso, en dos dimensiones, podemos tener
$$\int~r_{1}(t)~dt=F(t)+C_{1}~~y~~\int~r_{3}(t)~dt=G(t)+C_{2}$$
donde F y G son antiderivadas de $r_{1}(t)$ y $r_{2}(t)$, respectivamente. Entonces
\begin{align*} \int[r_{1}(t)+r_{2}(t)]~dt & =\left[\int~r_{1}(t)~dt\right]+\left[\int~r_{2}(t)~dt\right] \\ & =(F(t)+C_{1})+(G(t)+C_{2}) \\ & =F(t)+G(t)+C_{1}+C_{2} \\ & =F(t)+G(t)+C \end{align*}
donde $C=C_{1}i+C_{2}j$. Por lo tanto, la constante de integración se convierte en un vector constante.
Ejemplo. Calcula cada una de las siguientes integrales:
\begin{align*}
(a)&~\displaystyle{\int~[(3t^{2}+2t)i+(3t-6)j+(6t^{3}+5t^{2}-4)k]~dt}\\
(b)&~\displaystyle{\int~[(t,t^{2},t^{3})\times(t^{3},t^{2},t)]~dt}\\
(c)&~\displaystyle{\int_{0}^{\frac{\pi}{3}}~[\sin(2t)i+\tan(t)j+e^{-2t}k]~dt}
\end{align*}
(a) En este caso usamos la primera parte de la definición de la integral de una curva espacial:
\begin{align*} \int~[(3t^{2}+2t)i+(3t-6)j+(6t^{3}+5t^{2}-4)k]~dt&=\left[\int~(3t^{2}+2t)~dt\right]i+\left[\int~(3t-6)~dt\right]j \\ &+\left[\int~(6t^{3}+5t^{2}-4)~dt\right]k\\ &=\left(t^{3}+t^{2}\right)i+\left(\frac{3}{2}t^{2}-6t\right)j+\left(\frac{3}{2}t^{4}+\frac{5}{3}t^{3}-4t\right)k+C \end{align*}
(b) En este caso primero calcula $(t,t^{2},t^{3})\times (t^{3},t^{2},t)$
\begin{align*} (t,t^{2},t^{3})\times (t^{3},t^{2},t) & =\left|\begin{matrix}i&j&k\\t&t^{2}&t^{3}\\t^{3}&t^{2}&t\end{matrix}\right| \\ &=\left(t^{2}(t)-t^{3}(t^{2})\right)i-\left(t^{2}-t^{3}(t^{3})\right)j+\left(t(t^{2})-t^{2}(t^{3})\right)k \\ & =\left(t^{3}-t^{5}\right)i+\left(t^{6}-t^{2}\right)j+\left(t^{3}-t^{5}\right)k \end{align*}
A continuación, sustituya esto de nuevo en la integral e integre:
\begin{align*} \int~[(t,t^{2},t^{3})\times(t^{3},t^{2},t)]~dt&=\int~\left(t^{3}-t^{5}\right)i+\left(t^{6}-t^{2}\right)j+\left(t^{3}-t^{5}\right)k~dt \\ &=\left(\frac{t^{4}}{4}-\frac{t^{6}}{6}\right)i+\left(\frac{t^{7}}{7}-\frac{t^{3}}{3}\right)j+\left(\frac{t^{4}}{4}-\frac{t^{6}}{6}\right)k+C \end{align*}
(c) En este caso utilice la definición de la integral de una curva espacial:
\begin{align*} \int_{0}^{\frac{\pi}{3}}~[\sin(2t)i+\tan(t)j+e^{-2t}k]~dt&=\left[\int_{0}^{\frac{\pi}{3}}~\sin(2t)~dt\right]i+\left[\int_{0}^{\frac{\pi}{3}}~\tan(t)~dt\right]j+\left[\int_{0}^{\frac{\pi}{3}}~e^{-2t}~dt\right]k \\ &=\left(-\frac{1}{2}\cos(2t)\right)\Big{|}{0}^{\frac{\pi}{3}}i-\left(\ln(\cos(t))\right)\Big{|}{0}^{\frac{\pi}{3}}j-\left(\frac{1}{2}e^{-2t}\right)\Big{|}_{0}^{\frac{\pi}{3}}k \\
&=\left(-\frac{1}{2}\cos\frac{2\pi}{3}+\frac{1}{2}\cos(0)\right)i-(\ln\left(\cos\frac{\pi}{3}\right)-\ln(\cos(0)))j \\
&-\left(\frac{1}{2}e^{-\frac{2pi}{3}}-\frac{1}{2}e^{-2(0)}\right)k\\
&=\left(\frac{1}{4}+\frac{1}{2}\right)i-(-\ln(2))j-\left(\frac{1}{2}e^{-\frac{2\pi}{3}}-\frac{1}{2}\right)k\\
&=\frac{3}{4}i+(\ln(2))j+\left(\frac{1}{2}-\frac{1}{2}e^{-\frac{2\pi}{3}}\right)k.~~ \blacksquare
\end{align*}
Teorema.
Si $f=(f_{1}, \ldots,
f_{n})$ es continua sobre un intervalo $I$ y $a\,\epsilon\,I$
entonces:
$$\frac{d\displaystyle\int_{a}^{t}f}{dt}=f(t) \quad \forall \quad t\,\epsilon\,I$$
Demostración. En este caso se obtiene por la aplicación del primer teorema fundamental
del cálculo a cada una de las funciones componentes
\begin{align*} \int_{a}^{t}f(t)~dt&=\left(\int_{a}^{t}f_{1}(t)~dt, \ldots,\int_{a}^{t}f_{n}(t)~dt\right) \\ &=\left(\frac{d}{dt}\int_{a}^{t}f_{1}(t)~dt,ldots,\frac{d}{dt}\int_{a}^{t}f_{n}(t)~dt\right) \\ &=(f_{1}(t), \ldots , f_{n}(t)) \\ &= f(t).~~ \blacksquare \end{align*}
Teorema. Si $f(t)=(f_{1}(t), \ldots,
f_{n}(t))$ tiene derivada continua sobre un intervalo $I$, entonces
$\forall~~ a,b\,\in I,~~\displaystyle\int_{a}^{b}f'(t)=f(b)-f(a)$
Demostración.
\begin{align*} \int_{a}^{b}f’& =\int_{a}^{b}(f’_{1}, \ldots,f’_{n}) \\
& =\left( \displaystyle\int_{a}^{t}f’_{1}, \ldots, \displaystyle\int{a}^{t}f’_{n}\right) \\ & = \left( f_{1}(b)-f_{1}(a), \ldots,f_{n}(b)-f_{n}(a)\right)\\
& = f(b)-f(a).~~ \blacksquare
\end{align*}
Ejemplo.
Si $f(t)=(f_{1}(t),f_{2}(t),…,f_{n}(t))$ es integrable en $[a,b]$, para todo vector $C=(c_{1},c_{2},…,c_{n})$ entonces el producto escalar $C\cdot F$ es integrable en $[a,b]$ y $$C\cdot \int_{a}^{b} f(t)dt= \int_{a}^{b}C\cdot f(t)dt$$
En efecto tenemos que
\begin{align*} C\cdot \int_{a}^{b} f(t)dt&=(c_{1},c_{2},…,c_{n})\cdot\left(\int_{a}^{b} f_{1}(t)dt,\int_{a}^{b} f_{2}(t)dt,…,\int_{a}^{b} f_{n}(t)dt\right) \\ &=\left(c_{1}\cdot\int_{a}^{b} f_{1}(t)dt+c_{2}\cdot\int_{a}^{b} f_{2}(t)dt+…+c_{n}\cdot\int_{a}^{b} f_{n}(t)dt\right) \\ &=\left(\int_{a}^{b}c_{1}\cdot f_{1}(t)dt+,\int_{a}^{b} c_{2}\cdot f_{2}(t)dt+…+\int_{a}^{b}c_{n}\cdot f_{n}(t)dt\right) \\ &=\int_{a}^{b}C\cdot f(t) dt.~~ \blacksquare \end{align*}