Introducción

Las fórmulas de Frenet–Serret describen la geometría local de una curva suave en el espacio usando una triada de vectores unitarios que se desplaza a lo largo de la curva. Son fundamentales en cálculo diferencial de curvas y por tanto en sus aplicaciones inmediatas como en física, mecánica, robótica, entre otras.

Dada una curva $f:[a,b]\rightarrow\mathbb{R}^{n}$, el Vector Unitario Tangente $T$ es otra
función vectorial asociada a la curva, y está definida por:
$$\boxed{T(t)=\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\ \ \ \ \text{siempre
que $|f^{\prime}(t)| \neq 0$.}}$$
De acuerdo a la definición anterior tenemos
$$\|T(t)\|=\left\|\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right\|=\frac{\|f'(t)\|}{\|f'(t)\|}=1$$
y de acuerdo a lo anterior
\begin{align*} \|T(t)\|=1 &~\Rightarrow~T(t)\cdot T(t)=1 \\ &~\Rightarrow~\frac{d}{dt}(T(t)\cdot T(t))=0 \\ &~\Rightarrow~T'(t)\cdot T(t)+T(t)\cdot T'(t)=0 \\ &~\Rightarrow~2(T'(t)\cdot T(t))=0 \\ &~\Rightarrow~T'(t)\cdot T(t)=0 \end{align*}
lo que implica que $T'(t)$ es ortogonal $T(t)$. Si $T^{\prime}\neq 0$ el vector unitario que tiene la misma dirección que $T^{\prime}$ se llama Vector Normal Principal a la
curva y se designa por $N(t)$. Asi pues $N(t)$ es una nueva función vectorial asociada a la curva y esta dada por la ecuación:
$$\boxed{N(t)=\frac{T^{\prime}(t)}{\|T^{\prime}(t)\|}\ \ \ \ \text{si}\ \ \ \ \ \|T^{\prime}(t)\| \neq 0}$$
de acuerdo a lo visto con el vector tangente, se tiene que $T(t)$ y $N(t)$ son ortogonales.
Un tercer vector definido mediante
$$\boxed{B(t)=T(t)\times N(t)}$$
recibe el nombre de Vector Binormal. Notese que $$\|B(t)\|=\|T(t)\times
N(t)\|=\|T(t)\|\|N(t)\|\sin\left(\frac{\pi}{2}\right)=1$$
de acuerdo a lo anterior
\begin{align*} \|B(t)\|=1&~\Rightarrow~B(t)\cdot B(t)=1 \\ &~\Rightarrow~\frac{d}{dt}(B(t)\cdot B(t))=0 \\ &~\Rightarrow~B'(t)\cdot B(t)+B(t)\cdot B'(t)=0\\ &~\Rightarrow~ 2(B'(t)\cdot B(t))=0\\ &~\Rightarrow~B'(t)\cdot B(t)=0 \end{align*}
por tanto $B'(t)$ es ortogonal a $B(t)$. Es decir $\boxed{B'(t)\cdot B(t)=0}$

Ejemplo. Pruebe que $\displaystyle{B'(t)\cdot T(t)=0}$
Solución. Si $B(t)=T(t)\times N(t)$ entonces $B(t)$ es ortogonal a $T(t)$ y $B(T)$ es ortogonal a $N(t)$ y por lo tanto $B(t)\cdot T(t)=0$
Por otro lado
$$N(t)=\frac{T(t)}{\|T'(t)\|}~\Rightarrow~\|T'(t)\|~N(T)=T'(t)$$
Si $B(t)$ es ortogonal a $N(t)$ entonces $B(t)$ es ortogonal a $\|T'(t)\|~N(T)$. Por lo tanto
$$B(t)\cdot T'(t)=B(t)\cdot \|T'(t)\|~N(T)=0$$
Tenemos entonces que
\begin{align*} \frac{d}{dt}(B(t)\cdot T(t))=0&~\Rightarrow~B'(t)\cdot T(t)+B(t)\cdot T'(t)=0 \\ &~\Rightarrow~B'(t)\cdot T(t)+0=0 \\ &~\Rightarrow~B'(t)\cdot T(t)=0 \end{align*}
Por lo tanto $\boxed{B'(t)\cdot T(t)=0}$.$~~\blacksquare$
Según los resultados anteriores $B'(t)\cdot B(t)=0$ y $B'(t)\cdot T(t)=0$. Pero también $N(t)\cdot B(t)=0$ y $N(t)\cdot T(t)=0$. Por lo tanto $N(t)$ y $B'(t)$ deben ser paralelos, es decir existe $\alpha$ tal que $\boxed{B'(t)=\alpha N(t)}$.
Si la curva está parametrizada por longitud de arco, considerando que $\|\overline{f}'(s)\|=1$, se tiene
\begin{align*} T(s) & =\overline{f}'(s) \\ N(s) & =\frac{\overline{f}»(s)}{|\overline{f}»(s)|} \\ B(s) & =T(s)\times N(s) \end{align*}
$\fbox{Fórmulas de Frenet-Serret}$
El sistema de vectores ${T(t),N(t),B(t)}$ forman un triedro en el cual
$$\boxed{B(t)=T(t)\times N(t)}$$
de acuerdo a la definición anterior
\begin{align*} B(t)=T(t)\times N(t)&~\Rightarrow~N(t)\times B(t)=N(t)\times (T(t)\times N(t)) \\ &~\Rightarrow~N(t)\times B(t)=(N(t)\cdot N(t))T(t)-(N(t)\cdot T(t))N(t) \\ &~\Rightarrow~N(t)\times B(t)=T(t)-0\cdot N(t) \\ &~\Rightarrow~N(t)\times B(t)=T(t) \end{align*}
por tanto
$$\boxed{N(t)\times B(t)=T(t)}$$
Análogamente de acuerdo a la definición anterior
\begin{align*} B(t)=T(t)\times N(t)&~\Rightarrow~B(t)\times T(t)=(T(t)\times N(t))\times T(t) \\ &~\Rightarrow~B(t)\times T(t)=(T(t)\cdot T(t))N(t)-(N(t)\cdot T(t))T(t) \\ &~\Rightarrow~B(t)\times T(t)=N(t)-0\cdot T(t) \\ &~\Rightarrow~B(t)\times T(t)=N(t) \end{align*}
por tanto
$$\boxed{B(t)\times T(t)=N(t)}$$
Por que dicho sistema de vectores, es un conjunto ortonormal. Las fórmulas que dan las derivadas del triedro móvil, en términos del mismo triedro móvil, se llaman las fórmulas de Frenet-Serret.
Teorema
(a) $\displaystyle{\frac{dT}{ds}=\kappa N}$
(b) $\displaystyle{\frac{dB}{ds}=-\tau N(s)}$
(c) $\displaystyle{\frac{dN}{ds}=\tau B-\kappa T}$
$\fbox{Demostración}$
(a) Por definición $\displaystyle{N(s)=\frac{T'(s)}{\|T'(s)\|}}$ y $\displaystyle{\kappa(s)=\left\|\frac{dT}{ds}\right\|=\|f»(s)\|}$. Luego
$$T'(s)=\|T'(s)\|~N(s)=\kappa(s)~N(s).$$
(b) $\displaystyle{\frac{dB}{ds}=-\tau N(s)}$ es fórmula de definición de torsión.
(c) \begin{align*} N'(s)&=B'(s)\times T(s)+B(s)\times T'(s) \\ &=-\tau N(s)\times T(s)+B(s)\times \kappa N(s) \\ &=\tau T(s)\times N(s)-\kappa N(s)\times B(s) \\ &=\tau B(s)-\kappa T(s).~~\blacksquare \end{align*}

Más adelante

La siguiente entrada corresponde a la Unidad 2. El objetivo de la unidad es comprender las estructuras que permiten analizar el comportamiento de funciones y vectores en espacios más generales que la recta o el plano. Dos conceptos clave para ello son los espacios normados y la topología.

Tarea Moral

1.- Sea la curva $\mathbf{r}(t)=(t^2,t^3,t)$
a) Calcula el vector tangente unitario $T(t)$.
b) Calcula el vector normal $N(t)$.
c) Verifica que $T(t)\cdot N(t)=0$.

2.- Sea la curva $\mathbf{r}(t)=(t,t^2,t^3)$

a) Calcula $\mathbf{r}'(t)$ y $\mathbf{r}»(t)$.

b) Usa la fórmula de la curvatura $\kappa(t)=\frac{\|\mathbf{r}'(t)\times \mathbf{r}»(t)\|}{\|\mathbf{r}'(t)\|^3}$. Encuentra la curvatura en $t=1$.

3.-Sea $\gamma(t)=(a\cos(wt), a \sin(wt), bt), t\in \mathbb{R}$

a) Calcula la prametrización por longitud de arco de esta curva.

b) Calcula los vectores $T(s), N(s) y B(s)$ en cada punto de esta curva.

4.- Dada la hélice $\mathbf{r}(t)=(\cos t,\sin t,t)$

a) Calcula los vectores $T(t)$, $N(t)$ y $B(t)$.
b) Verifica que forman un sistema ortonormal, es decir,
$T\cdot N=N\cdot B=B\cdot T=0.$

5.- Sea $\mathbf{r}(t)$ una curva regular en $\mathbb{R}^3$ parametrizada por longitud de arco $s$, y sea $T(s)=\frac{d\mathbf{r}}{ds}$
su vector tangente unitario. Demuestra que el vector derivada $\dfrac{dT}{ds}$ es ortogonal a $T(s)$; es decir, $T(s)\cdot \frac{dT}{ds}=0$

Sugerencia: utiliza que $T(s)$ es unitario, es decir, $T(s)\cdot T(s)=1.$
Deriva esta igualdad respecto a $s$.

Enlaces

El siguiente enlace de geogebra contiene un interactivo que muestra como el plano osculador recorre una curva parametrizada. Aunque el ejemplo contiene una curva definida, tú puedes construir tu propio ejemplo definiendo las entradas de la curva con nombre f, g y h.

Es importante notar que en la construcción se define primero el vector tangente en un punto (usando un deslizador)

https://www.geogebra.org/3d/mmumcb3g

Introducción

En el estudio del cálculo diferencial, las curvas no solo se analizan por su forma visible, sino también por cómo cambian localmente en cada punto. Conceptos como la curvatura, el radio de curvatura, el círculo osculador y la torsión permiten describir con precisión el comportamiento geométrico de una curva tanto en el plano como en el espacio.

En una recta, el vector unitario tangente $T$ no cambia su dirección y por tanto $T^{\prime}=0$. Si la curva no es una linea recta, la derivada $T^{\prime}$ mide la tendencia de la tangente a cambiar su dirección. El coeficiente de variación o derivada de la tangente unitaria respecto a la longitud de arco se denomina vector curvatura de la curva. Se designa por $\displaystyle{dT/ds}$ donde s representa la
longitud de arco.

Sea $f:[a,b]\subset\mathbb{R}\rightarrow\mathbb{R}^{n}$ una curva dos veces diferenciable parametrizada por longitud de arco y T su vector tangente unitario. La curvatura de f es la función
$$\kappa=\left\|\frac{dT}{ds}\right\|=\|f^{\prime\prime}(s)\|$$
La letra $\kappa$ es la letra griega kappa. La curvatura mide la flexión de la curva.
Mostraremos que una recta, es una curva que no se flexiona, tiene curvatura 0
Ejemplo. Calcule la curvatura en todo punto de la recta $f(t)=(x_{0},y_{0},z_{0})+t(u_{1},u_{u},u_{3})$ donde $\|u\|=1$
tenemos:
\[ f^{\prime}(t)=(u_{1},u_{2},u_{3})\ \ \ \ \ \text{y}\ \ \ \ \ \|f^{\prime}(t)\|=\|u\|=1
\]
Por lo tanto la curva esta parametrizada por longitud de arco
Por lo tanto $\kappa=\|f^{\prime\prime}(t)\|=0$, por lo tanto
$\kappa=0$.$~~\blacksquare$
Ejemplo Calcule la curvatura de una circunferencia. Para un círculo de radio $R$ dado por la ecuación
$$f(t)=(R\cos t,R \sin t)$$
tenemos:
La parametrizacion por longitud de arco es:
$$s=\int_{0}^{t}\|f'(u)\|du=\int_{0}^{t}Rdt=Rt~\rightarrow~s=Rt~\Rightarrow~t=\frac{s}{R}$$
de esta manera se tiene
\begin{align*} \overline{f}(s) &=f\left(\frac{s}{R}\right)=\left(R\cos\left(\frac{s}{R}\right),R\sin\left(\frac{s}{R}\right)\right) \\ \overline{f}^{\prime}(s)&=\left(-\sin \left(\frac{s}{R}\right), \cos \left(\frac{s}{R}\right)\right) \\ \overline{f}^{\prime\prime}(s)&=\left(-\frac{1}{R}\cos \left(\frac{s}{R}\right),-\frac{1}{R} \sin \left(\frac{s}{R}\right)\right) \end{align*}
Por lo tanto $\displaystyle{\kappa=\|\overline{f}^{\prime\prime}(s)\|=\frac{1}{R}}$.
Esto prueba que una circunferencia tiene curvatura constante.
El siguiente teorema nos proporciona otras fórmulas que nos permiten calcular la
curvatura parametrizada por otro parámetro t, que no es necesariamente la longitud
de arco.
Teorema. Sea $f(t)$ una curva dos veces diferenciable. Entonces
$$\kappa(t)=\frac{\|T'(t)\|}{\|f'(t)\|}$$
Demostración. Sabemos que $\displaystyle{s^{\prime}(t)=\|f^{\prime}(t)\|}$. Además usando la regla de la cadena
$\begin{align*} T'(t)&=\frac{dT}{dt}=\frac{dT}{ds}\frac{ds}{dt}=\frac{dT}{ds}\|f'(t)\| \\ &~\Rightarrow~\frac{dT}{ds}=\frac{T'(t)}{\|f'(t)\|} \\ &~\Rightarrow~\left\|\frac{dT}{ds}\right\|=\frac{\|T'(t)\|}{\|f'(t)\|} \\ &~\Rightarrow~\kappa(t)=\frac{\|T'(t)\|}{\|f'(t)\|}.~~ \blacksquare \end{align*}$
Ejemplo.
Calcule la curvatura $\kappa$ de la hélice
$x(t)=a\cos(wt)$, $y(t=a\sin(wt))$, $z(t)=bt$.
Solución. Tenemos que: \[f^{\prime}(t)=(-wa\sin(wt),aw\cos(wt),b)\ \ \Rightarrow\ \ \|f^{\prime}(t)\|=\sqrt{a^2w^2+b^2}\] Por lo tanto \[ T=(-aw\sin(wt),aw\cos(wt),b)\frac{1}{\sqrt{a^2w^2+b^2}} \] Por lo tanto \[ k=\frac{\|T^{\prime}\|}{\|f^{\prime}\|}= \|-aw^2\cos(wt),-aw^2\sin(wt),0\|\frac{1}{\sqrt{a^2w^2+b^2}}= \] \[ =\sqrt{(aw^2)^2(\cos^2(wt)+\sin^2(wt))}\ \frac{1}{\sqrt{a^2w^2+b^2}}= \frac{aw^2}{\sqrt{a^2w^2+b^2}}.~~ \blacksquare \]

Teorema . Sea $f(t)$ una curva dos veces diferenciable. Entonces
$$\kappa(t)=\frac{\|f^{\prime}(t)\times f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{3}}$$
Demostración. Si $$T=\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\Rightarrow
T~\|f^{\prime}(t)\|=f^{\prime}(t)\Rightarrow
T\frac{ds}{dt}=f^{\prime}(t)$$Por lo tanto
$$f^{\prime\prime}(t)=T\frac{d^{2}s}{dt^{2}}+\frac{ds}{dt}T^{\prime}$$
Haciendo el producto cruz $$f^{\prime}(t)\times
f^{\prime\prime}(t)=T\frac{ds}{dt}\times
\left(T\frac{d^{2}s}{dt^{2}}+\frac{ds}{dt}T^{\prime}\right)=\cancel{T\frac{ds}{dt}\times
T\frac{d^{2}s}{dt^{2}}}+T\frac{ds}{dt}\times
\frac{ds}{dt}T^{\prime}$$Por lo tanto
$$\|f^{\prime}(t)\times f^{\prime\prime}(t)\|=\left\|T\frac{ds}{dt}\times
\frac{ds}{dt}T^{\prime}\right\|=\left(\frac{ds}{dt}\right)\left\|T\right\|\left(\frac{ds}{dt}\right)\left\|T^{\prime}\right\|\sin(T,T^{\prime})=\left(\frac{ds}{dt}\right)^{2}\left\|T^{\prime}\right\|$$En
cosecuencia$$\frac{\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|}{\left(\frac{ds}{dt}\right)^{2}}=\|T^{\prime}|\Rightarrow
\|T^{\prime}\|=\frac{\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{2}}$$ sustituimos en
$$k(t)=\frac{\|T^{\prime}(t)\|}{\|f^{\prime}(t)\|}\Rightarrow \kappa(t)=\frac{\frac{\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{2}}}{\|f^{\prime}(t)\|}\Rightarrow
\kappa(t)=\frac{\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{3}}.~~ \blacksquare $$
Ejemplo. Hallar la función curvatura $\kappa(t)$ de la curva
$$f(t)=\left(t^{2},t,\frac{2t^{3}}{3}\right)$$
Solución. Según la fórmula anterior
\begin{align*} f'(t) & =(2t,1,2t^{2}) \\\ f^{\prime\prime}(t) & =(2,0,4t) \\ \|f'(t)\| & =\sqrt{4t^{2}+1+4t^{4}}=2t^{2}+1 \end{align*}
Por lo que
\begin{align*} f'(t)\times f^{\prime\prime}(t) & =\left|\begin{matrix}i&j&k\\2t&1&2t^{2}\\2&0&4t\end{matrix}\right| \\ & =2(2t,-2t^{2},-1) \\ \|f'(t)\times f^{\prime\prime}(t)\|&=2\sqrt{4t^{2}+4t^{4}+1}=2(2t^{2}+1) \end{align*}
Luego
$$\kappa(t)=\frac{\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{3}}=\frac{2(2t^{2}+1)}{(2t^{2}+1)^{3}}=\frac{2}{(2t^{2}+1)^{2}}.~~ \blacksquare $$
Ejemplo. Para el caso especial de una curva plana con ecuación $y=f(x)$ podemos escoger $x$ como el parámetro y escribir $r(x)=x\hat{i}+f(x)\hat{j}$ entonces
\begin{align*}r^{\prime}(x)&=\hat{i}+f^{\prime}(x)\hat{j}\\r^{\prime
\prime}(x)&=f^{\prime \prime}(x)\hat{j}\end{align*} y al efectuar:
\[
r^{\prime}(x)\ \text{x}\ r^{\prime \prime}(x)=
\left|
\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & f^{\prime}(x) & 0 \\
0 & f^{\prime \prime}(x) & 0 \\
\end{array}
\right|= f^{\prime \prime}(x)\hat{k}
\]

Por lo tanto $\|r^{\prime}(x)\ \times r^{\prime\prime}(x)\|=|f^{\prime\prime}(x)|$.
Por lo tanto, para una curva plana
\[
\kappa(x)=\frac{\|r'(t)\times r^{\prime\prime}(t)\|}{\|r'(t)\|^{3}}=\frac{|f^{\prime\prime}(x)|}{\left(1+[f^{\prime}(x)]^2\right)^{3/2}}.~~ \blacksquare
\]
Ejemplo. Calcular la curvatura del gráfico $f(x)=e^{-x}$.
Solución. Tenemos que: $f'(x)=-e^{-x}$ y $f^{\prime\prime}(x)=e^{-x}$. Luego
$$\kappa(x)=\frac{|f^{\prime\prime}(x)|}{\left[1+\left(f'(x)\right)^{2}\right]^{\frac{3}{2}}}=\frac{e^{-x}}{\left[1+\left(-e^{-x}\right)^{2}\right]^{\frac{3}{2}}}=\frac{e^{-x}}{\left[e^{-2x}+1\right]^{\frac{3}{2}}}.~~ \blacksquare$$

Circunferencia y radio de curvatura

Sea $f:[a,b]\rightarrow\mathbb{R}^{2}$ una curva plana y un punto $P$ sobre una curva plana donde $\kappa\neq 0$. Se llama circunferencia de curvatura o circunferencia osculadora de la curva en el punto P a la circunferencia que cumple las siguientes condiciones:
(a) Es tangente a la curva en P. (la circunferencia y la curva tienen la misma recta tangente en el punto P).
(b) Tiene la misma curvatura ($\kappa$) que la curva en P.
(c) Se encuentra hacia el lado concavo o interior de la curva.
(d) El radio de la curvatura de la curva P es el radio del círculo de curvatura o círculo osculador. $$\rho(t)=\frac{1}{\kappa(t)}$$

Asi el centro del círculo osculador (llamado centro de curvatura)
debe estar en:

\[
c(t)=f(t)+\frac{1}{k(t)}N(t)
\]
Ejemplo. Determine los vectores $T$ y $N$, la curvatura $k$, el centro de la curvatura y la circunferencia osculadora de la parábola $y=x^2$ en el punto $(1,1)$.
Solución. Si la parábola esta
parametrizada por $x=t$ y por $y=t^2$, entonces su vector de
posición es $f(t)=(t,t^2)$, por lo tanto
\begin{align*}f(t)=(t,t^2)&\Rightarrow f^{\prime}(t)=(1,2t)\\&\Rightarrow\|f^{\prime}(t)\|=\sqrt{1+4t^2}\\&\Rightarrow f^{\prime\prime}(t)=(0,2)\end{align*}
por lo tanto:
\[ T(t)=\frac{(1,2t)}{\sqrt{1+4t^2}}\ \ \ \ \ \ \ T(1)=\left(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}}\right)\ \ \ \ \ \ \ N(1)=\left(\frac{-2}{\sqrt{5}},\frac{1}{\sqrt{5}}\right) \] la curvatura $\kappa$, \[ k=\frac{\|f^{\prime\prime}(t)\|}{\left(\sqrt{1+[f^{\prime}(t)]^2}\right)^3}= \frac{2}{\left(\sqrt{1+4t^2}\right)^3}\ \ \ \ \ \ \ k(1)=\frac{2}{5\sqrt{5}}\ \ \Rightarrow\ \ \rho=\frac{5\sqrt{5}}{2} \] Por lo tanto el centro de la curvatura es \[ c(t)=f(1,1)+\frac{1}{\frac{2}{5\sqrt{5}}}\left(\frac{-2}{\sqrt{5}},\frac{1}{\sqrt{5}}\right)= \left(-4,\frac{7}{2}\right) \] Y la ecuación del círculo osculador a la parábola es, por tanto: \[ (x+4)^2+\left(y-\frac{7}{2}\right)^2= \left(\frac{5\sqrt{5}}{2}\right)^2=\frac{125}{4}.~~ \blacksquare \]

Torsión

Sea $f:I\subset \mathbb{R}\rightarrow \mathbb{R}^{3}$ una curva tres veces diferenciable parametrizada por longitud de arco. Nuestro objetivo consistira en estimar con que rapidez una curva se aleja de su plano osculador

La forma de medir la rapidez de alejamiento de la curva f de su plano osculador es por medio del vector binormal $B(s)=T(s)\times N(s)$, que sabemos es un vector unitario ortogonal al plano osculador de f en P. Puesto que $\|B(s)\|=1$, $\forall~s\in I$, la magnitud de la derivada $\|B'(s)\|$ de $B(s)$ medirá precisamente la rapidez con la que el vector binormal $B(s)$ está cambiando de dirección en los alrededores del punto estudiado.
Puesto que $B(s)=T(s)\times N(s)$, tenemos, derivando
$$B'(s)=T(s)\times N'(s)+T'(s)\times N(s)$$
El sumando $T'(s)\times N(s)$ que aparece en esta expresión es igual a cero, ya que $T'(s)=f^{\prime\prime}(s)$ es un vector en la dirección de $N(s)$ (y por lo tanto son colineales; por lo que su producto cruz es cero). Entonces nos queda
$$B'(s)=T(s)\times N'(s)$$
También tenemos que
$$\|B\|=1~\Rightarrow~\frac{d \|B\|^{2}}{ds}=0~\Rightarrow~\frac{d(B\cdot B)}{ds}=0~\Rightarrow~B\cdot B’+B’\cdot B=0~\Rightarrow~B’\cdot B=0~\Rightarrow~B’\bot B $$ Esto nos permite concluir que $B'(s)$ es un vector en el plano osculador de f en s. Por otro lado $$B\cdot T=0~\Rightarrow~(B\cdot T)’=0~\Rightarrow~B’\cdot T+T’\cdot B=0~\underbrace{\Rightarrow}_{\textcolor{red}{T’\cdot B=N~ \|T’\|\cdot B=0}}~B’\cdot T=0~\Rightarrow~B’\bot T$$
De lo anterior podemos concluir que $B’$ tiene la dirección del vector $N$. Debe entonces existir un escalar $\tau(s)$ tal que
$$B'(s)=\tau(s)N(s)$$
Definición. Sea $f:I\subset \mathbb{R}\rightarrow \mathbb{R}^{3}$ una curva tres veces diferenciable parametrizada por longitud de arco tal que $f»(s)\neq 0$ $\forall~s\in I$. El número $\tau(s)$ tal que $B'(s)=-\tau(s)N(s)$ se llama torsión de f en s.
Notese que
$$\|B'(s)\|=|\tau(s)|$$
Ejemplo. Dada la función
$$f(t)=(\cos(t),\sin(t),t)$$
cuya reparametrización por longitud de arco es:
$$\overline{f}(s)=\left(\cos\left(\frac{s}{\sqrt{2}}\right),\sin\left(\frac{s}{\sqrt{2}}\right),\frac{s}{\sqrt{2}}\right)$$
cuyo vector normal es
$$N(s)=\left(-\cos\left(\frac{s}{\sqrt{2}}\right),-\sin\left(\frac{s}{\sqrt{2}}\right),0\right)$$
cuyo vector binormal es
$$B(s)=\frac{1}{\sqrt{2}}\left(\sin\left(\frac{s}{\sqrt{2}}\right),-\cos\left(\frac{s}{\sqrt{2}}\right),1\right)$$
de modo que
$$B'(s)=\frac{1}{2}\left(\cos\left(\frac{s}{\sqrt{2}}\right),\sin\left(\frac{s}{\sqrt{2}}\right),0\right)$$
y por lo tanto se tiene
$$|\tau(s)|=\|B'(s)\|=\frac{1}{2}.~~ \blacksquare$$
Una curva es plana (es decir, es la imagen de un camino $f:[a,b]\rightarrow\mathbb{R}^{3}$ tal que f(s) se encuentra en un plano en $\mathbb{R}^{3}$ para toda $s\in [a,b]$) si y sólo si su torsión es igual a cero $(\forall~s\in [a,b])$.
En efecto, si $\tau(s)=0$, se tiene que $B'(s)=0$, por lo que el vector binormal $B(s)$ debe ser constante, es decir $B(s)=v$ para todo $s\in[a,b]$. De aquí se tiene que
$$f'(s)\cdot B(s)=f'(s)\cdot v=0~~~\forall~s\in[a,b]$$
(pues $f'(s)$ es ortogonal a $B(s)$), o sea
$$\frac{d(f(s)\cdot v)}{ds}=0$$
de donde $f(s)\cdot v=cte~~~\forall~s\in[a,b]$, y por lo tanto, concluimos que $f(s)$ se encuentra en el plano cuyo vector normal es v, $\forall~s\in[a,b]$.

Recíprocamente, si $f(s)$ se encuentra en un plano para toda s en $[a,b]$, entonces dicho plano es el plano osculador de la curva en todo punto de ella, por tanto el vector unitario $B(s)$ no cambia de dirección, por lo que $B'(s)=0$. de donde $\tau(s)=0$ para toda s en $[a,b]$. $\blacksquare$

Fórmula para calcular la Torsión en términos de la parametrización por longitud de arco

La torsión representa una variación en la dirección del vector binormal, procederemos ahora a desarrollar una fórmula para calcularla
Sea $\overline{f}:[a,b]\rightarrow\mathbb{R}^{3}$ la reparametrización por longitud de arco de f, $\overline{f}=f\circ\varphi$. Queremos calcular la torsión de f en t, donde $t=\varphi(s)$. Sabemos que
\begin{align*} T(s) & =\overline{f}'(s)=\frac{f'(t)}{\|f'(t)\|} \\ T'(s)&=\overline{f}»(s)=\frac{d\left(\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)}{ds} \\ &=\frac{d\left(\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)}{dt}\frac{dt}{ds}=\frac{d\left(\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)}{dt}\frac{1}{\frac{ds}{dt}}\\ &=\frac{d\left(\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)}{dt}\frac{1}{\varphi^{\prime}(s)}\\ &=\frac{d\left(\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)}{dt}\frac{1}{\|f^{\prime}(t)\|}\\ &=\left(\frac{\|f^{\prime}(t)\|f^{\prime\prime}-f^{\prime}(t)\frac{d\left(\|f^{\prime}(t)\|\right)}{dt}}{\|f^{\prime}(t)\|^{2}}\right)\frac{1}{\|f^{\prime}(t)\|}\\ &=\left(\frac{\|f^{\prime}(t)\|f^{\prime\prime}-f^{\prime}(t)\frac{f^{\prime}\cdot f^{\prime\prime}}{\|f^{\prime}(t)\|}}{\|f^{\prime}(t)|^{2}}\right)\frac{1}{\|f^{\prime}(t)\|}~~\left(\frac{d\left(\|f^{\prime}(t)\|\right)}{dt}=\frac{d\sqrt{f^{\prime}(t)\cdot f^{\prime}(t)}}{dt}=\frac{f^{\prime}(t)\cdot f^{\prime\prime}(t)}{\|f^{\prime}(t)\|}\right)\\ &=\left(\frac{\|f^{\prime}(t)\|^{2}f^{\prime\prime}-\left(f^{\prime}(t)\cdot f^{\prime\prime}(t)\right)f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)\frac{1}{\|f^{\prime}(t)\|^{3}}\\ &=\frac{1}{\|f^{\prime}(t)\|^{4}}\left(\|f^{\prime}(t)\|^{2}f^{\prime\prime}(t)-\left(f^{\prime}(t)\cdot f^{\prime\prime}(t)\right)f^{\prime}(t)\right)\\ N(s) &=\frac{\overline{f}^{\prime\prime}(s)}{\kappa(s)} =\frac{\overline{f}^{\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|} \end{align*}
calculemos
$$B'(s)=T(s)\times N'(s)$$ en este caso
\begin{align*} N^{\prime}(s) & =\frac{\|\overline{f}^{\prime\prime}(s)\|\overline{f}^{\prime\prime\prime}(s)-\overline{f}^{\prime\prime}(s)\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|}\right)}{\|\overline{f}^{\prime\prime}(s)\|^{2}} \\ &=\frac{\overline{f}^{\prime\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|}-\overline{f}^{\prime\prime}(s)\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|^{3}}\right) \end{align*}
Luego si $B^{\prime}(s)=T(s) \times N^{\prime}(s)$ entonces se tiene que
\begin{align*} B^{\prime}(s) &=\overline{f}^{\prime}(s)\times \left(\frac{\overline{f}^{\prime\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|}-\overline{f}^{\prime\prime}(s)\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|^{3}}\right)\right) \\ &=\frac{1}{|\overline{f}^{\prime\prime}(s)|}\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime\prime}(s)-\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|^{3}}\right)\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime}(s) \end{align*}
La torsión esta dada por
\begin{align*} B^{\prime}(s) &=\tau(s)N(s) \\ &\Rightarrow B^{\prime}(s)\cdot N(s)=\tau(s)N(s)\cdot N(s) \\ &\Rightarrow B^{\prime}(s)\cdot N(s)=\tau(s)\|N(s)\|^{2} \\ &\Rightarrow B^{\prime}(s)\cdot N(s)=|\tau(s)| \end{align*}
Entonces
\begin{align*} \tau(s) &=B^{\prime}(s)\cdot N(s) \\ &=\left(\frac{1}{\|\overline{f}^{\prime\prime}(s)\|}\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime\prime}(s)-\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|^{3}}\right)f^{\prime}(s)\times \overline{f}^{\prime\prime}(s)\right)\cdot \frac{\overline{f}^{\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|} \\ &=\frac{1}{\|\overline{f}^{\prime\prime}(s)\|^{2}}\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime\prime}(s)\cdot \overline{f}^{\prime\prime}(s)-\cancel{\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|^{4}}\right)\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime}(s)} \\ &=\frac{1}{\|\overline{f}^{\prime\prime}(s)\|^{2}}\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime\prime}(s)\cdot \overline{f}^{\prime\prime}(s) \end{align*}
La cancelación es porque $$\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime}(s)\cdot
\overline{f}^{\prime\prime}(s)=0$$ y como $$k(s)=\|\overline{f}^{\prime\prime}\|$$ se
tiene entonces que $$\boxed{\tau(s)=\frac{\overline{f}^{\prime}(s)\times
\overline{f}^{\prime\prime\prime}(s)\cdot \overline{f}^{\prime\prime}(s)}{k(s)^{2}}=-\frac{\overline{f}^{\prime}(s)\times
\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{k(s)^{2}}}$$

Fórmula para calcular la Torsión en términos del parámetro t

Ahora vamos a expresar la torsión en términos de t. Ya hemos visto que
\begin{align*} \overline{f}^{\prime}(s)&=\frac{f^{\prime}(t)}{|f^{\prime}(t)|} \\ f^{\prime\prime}(s) & =\frac{1}{\|f^{\prime}(t)\|^{4}}\left(|f^{\prime}(t)|^{2}f^{\prime\prime}(t)-\left(f^{\prime}(t)\cdot f^{\prime\prime}(t)\right)f^{\prime}(t)\right) \end{align*}
Por lo tanto
\begin{align*} f^{\prime}(s)\times f^{\prime\prime}(s) &=\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\times \left(\frac{1}{\|f^{\prime}\|^{4}}\left(\|f^{\prime}(t)\|^{2}f^{\prime\prime}(t)-\left(f^{\prime}(t)\cdot f^{\prime\prime}(t)\right)f^{\prime}(t)\right)\right) \\ &=\left(\frac{1}{\|f^{\prime}(t)\|^{3}}\right)f^{\prime}(t)\times f^{\prime\prime}(t)-\left(\frac{f^{\prime}(t)\cdot f^{\prime\prime}(t)}{\|f^{\prime}(t)\|^{5}}\right)\cancel{f^{\prime}(t)\times f^{\prime}(t)} \\ &=\left(\frac{1}{\|f^{\prime}(t)\|^{3}}\right)f^{\prime}(t)\times f^{\prime\prime}(t) \end{align*}
Mientras que
\begin{align*} f^{\prime\prime\prime}(s) &=\frac{df^{\prime\prime}(s)}{ds}=\left(\frac{df^{\prime\prime}(s)}{dt}\right)\frac{dt}{ds}=\left(\frac{df^{\prime\prime}(s)}{dt}\right)\frac{1}{\frac{ds}{dt}} \\ &=\left(\frac{df^{\prime\prime}(s)}{dt}\right)\frac{1}{\|f^{\prime}(t)\|} \\ &=\frac{1}{\|f^{\prime}(t)\|}\frac{d}{dt}\left(\frac{1}{\|f^{\prime}\|^{4}}\left(\|f^{\prime}(t)\|^{2}f^{\prime\prime}(t)-\left(f^{\prime}(t)\cdot f^{\prime\prime}(t)\right)f^{\prime}(t)\right)\right) \\ &=\left(\frac{1}{\|f^{\prime}(t)\|}\right)\left[\left(\frac{1}{\|f^{\prime}(t)\|^{2}}f^{\prime\prime}(t)\right)+\left(\frac{1}{\|f^{\prime}(t)\|^{2}}\right)^{\prime}f^{\prime\prime}(t)\right. \\ &\left.-\left(\frac{f^{\prime}(t)\cdot f^{\prime\prime}(t)}{\|f^{\prime}(t)\|^{4}}\right)f^{\prime\prime}(t)-f^{\prime}(t)\left(\frac{f^{\prime}(t)\cdot f^{\prime\prime}(t)}{\|f^{\prime}(t)\|^{4}}\right)^{\prime}~\right] \end{align*}
Por lo tanto
\begin{align*} f^{\prime}(s)\times f^{\prime\prime}(s)\cdot f^{\prime\prime\prime}(s) &=\left(\frac{1}{\|f^{\prime}(t)\|^{3}}\right)f^{\prime}(t)\times f^{\prime\prime}(t)\cdot \left(\frac{1}{\|f^{\prime}(t)\|}\right)\left[\left(\frac{1}{\|f^{\prime}(t)\|^{2}}f^{\prime\prime}(t)\right)\right. \\ &\left.+\cancel{\left(\frac{1}{\|f^{\prime}(t)\|^{2}}\right)^{\prime}f^{\prime\prime}(t)}-\cancel{\left(\frac{f^{\prime}(t)\cdot f^{\prime\prime}(t)}{\|f^{\prime}(t)\|^{4}}\right)f^{\prime\prime}(t)}-\cancel{f^{\prime}(t)\left(\frac{f^{\prime}(t)\cdot f^{\prime\prime}}{\|f^{\prime}(t)\|^{4}}\right)^{\prime}}~\right] \\ &=\frac{1}{\|f^{\prime}(t)\|^{3}}f^{\prime}(t)\times f^{\prime\prime}(t)\cdot \frac{1}{\|f^{\prime}(t)\|^{3}}f^{\prime\prime\prime}(t) \\ &=\frac{1}{\|f^{\prime}(t)\|^{6}}f^{\prime}(t)\times f^{\prime\prime}(t)\cdot f^{\prime\prime\prime}(t) \end{align*}
finalmente
\begin{align*} \tau(t) &=\frac{f^{\prime}(s)\times f^{\prime\prime\prime}(s)\cdot f^{\prime\prime}(s)}{k(s)^{2}} \\ &=-\frac{f^{\prime}(s)\times f^{\prime\prime}(s)\cdot f^{\prime\prime\prime}(s)}{k(s)^{2}} \\ &=-\frac{1}{\|f^{\prime}(t)\|^{6}}\frac{f^{\prime}(t)\times f^{\prime\prime}(t)\cdot f^{\prime\prime\prime}}{\left(\frac{\|f^{\prime}\times f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{3}}\right)^{2}} \end{align*}
Tenemos que
la torsión esta dada por $$\boxed{\tau(t)=-\frac{f^{\prime}(t)\times
f^{\prime\prime}(t)\cdot
f^{\prime\prime\prime}(t)}{\left(\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|\right)^{2}}}$$
Ejemplo. Probar que la torsión de la hélice $f(t)=(a\cos(t),a\sin(t),bt)$ es
$$\tau(t)=\frac{b}{a^{2}+b^{2}}$$
Solución. En este caso
\begin{align*} f'(t) & =(-a\sin(t),a\cos(t),b) \\ f^{\prime\prime}(t) & =(-a\cos(t),-a\sin(t),0) \\ f^{\prime\prime\prime}(t) & =(a\sin(t),-a\cos(t),0) \end{align*}
Por lo que
$$f'(t)\times f^{\prime\prime}(t)=\left|\begin{matrix}i&j&k\\-a\sin(t)&a\cos(t)&b\\-a\cos(t)&-a\sin(t)&0\end{matrix}\right|=(ab\sin(t),-ab\cos(t),a^{2})$$
tenemos entonces
$$f'(t)\times f^{\prime\prime}(t)\cdot f^{\prime\prime\prime}(t)=(ab\sin(t),-ab\cos(t),a^{2})\cdot (a\sin(t),-a\cos(t),0)=a^{2}b$$
$$\|f'(t)\times f»(t)\|=\|(ab\sin(t),-ab\cos(t),a^{2})\|=\sqrt{a^{2}b^{2}+a^{4}}=|a|\sqrt{a^{2}+b^{2}}$$
luego,
$$\tau(t)=\frac{[f'(t)\times f^{\prime\prime}(t)]\cdot f^{\prime\prime\prime}(t)}{\|f'(t)\times f^{\prime\prime}(t)\|^{2}}=\frac{a^{2}b}{\left(|a|\sqrt{a^{2}+b^{2}}\right)^{2}}=\frac{b}{a^{2}+b^{2}}.~~ \blacksquare$$

Más adelante

En la siguiente entrada veremos cómo las curvaturas de las ecuaciones polares determinadas por los vectores tangente, normal y binormal dan origen a las fórmulas de Frenet-Serret. En la geometría de las curvas dichas fórmulas juegan un papel importante.

Tarea Moral

1.- Determine la curvatura de la parábola: $y=4px^2$

2.- Demuestra que $N´=-kl´T´+tl’B$

3.- Determina la torsión de la cúbica descrita por $f(t)=(t,t^2,t^3)$

4.-Determina la torsión de la hélice cónica descrita por $f(t)=(tcost, tsent, t)$ en el punto $(0,0,0)$.

5.- Determina la torsión de la curva descrita por $f(t)=(t-sent, 1-cost,t)$ en los puntos: $t=0$, $t=\dfrac{\pi}{2}$, $t=\pi$

Enlaces

El siguiente enlace muestra una construcción en geogebra sobre el trazo de circunferencia osculadora de la curva $cos(2x)$

https://www.geogebra.org/calculator/afgf3mmq?embed

https://www.geogebra.org/calculator/vararydy

La siguiente entrada muestra varios ejemplos de caústicas, una cáustica en matemáticas es una curva generada apartir de los centros de curvatura de otra curva dada.

Caustic Curves and the Optics of Rays

El siguiente enlace muestra una página que aborda una aplicación física sobre la «curva caústica» generada por un fenómeno óptico.

https://abel.math.harvard.edu/archive/21a_spring_06/exhibits/coffeecup/index.html#:~:text=The%20coffeecup%20caustic,It%20is%20stable.

Cuando la luz incide sobre el borde interior de una taza circular, como una taza de café, se forma en el interior una curva luminosa brillante con forma de corazón.

Introducción

calcular la longitud de arco de una curva no solo nos permite medir “cuánto mide” la trayectoria, sino que también nos introduce de manera natural en la idea de cómo cambia la curva punto a punto. Es precisamente en este contexto donde surgen de manera natural los vectores tangente, normal y binormal.

Plano Tangente

Sea $f:[a,b]\rightarrow\mathbb{R}^{n}$ una curva tal que el vector derivada $f'(t)\neq 0$ para todo $t\in[a,b]$, es tangente a f y apunta en la dirección que el parámetro t crece.
Definición. Dada una curva $f:[a,b]\rightarrow\mathbb{R}^{n}$, el vector unitario tangente $T$ es otra función vectorial asociada a la curva, y está definida por:
\[
T(t)=\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\ \ \ \ \text{si}\ \ \ \|f^{\prime}(t)\| \neq 0.
\]
Si en la definición anterior, la curva está parametrizada por longitud de arco, considerando que $\|\overline{f}'(s)\|=1$, se tiene que
$$T(s)=\overline{f}'(s)$$

Propiedades del Vector Tangente

(a) En este caso se tiene que
\[
\|T(t)\|= \left\| \frac{f^{\prime}(t)}{\|f^{\prime}(t)\|} \right\|=
\frac{1}{\|f^{\prime}(t)\|} \|f^{\prime}(t)\|=1
\]
por lo tanto $T$ es de magnitud constante.
(b) Tenemos que
\begin{align*} \|T(t)\|=1&\Rightarrow \|T(t)\|^2=1\\&\Rightarrow \frac{d}{dt}\left(\|T(t)\|^2\right)=0\\&\Rightarrow \frac{d}{dt}\left(T(t)\cdot T(t)\right)=0\\&\Rightarrow T'(t)\cdot T(t)+T(t)\cdot T'(t)=0\\&\Rightarrow 2T(t)\cdot T'(t)=0\\&\rightarrow T(t)\cdot T'(t)=0\end{align*}
Esto es $T(t)$ y $T'(t)$ son ortogonales. Este resultado nos permite definir un vector unitario ortogonal a $T(t)$ y que tiene la misma dirección que $T'(t)$.

Vector Normal Principal

Definición. Si $\|T^{\prime}(t)\|\neq 0$ el vector unitario que tiene la misma dirección que $T^{\prime}$ se llama Normal Principal a la curva y se designa por $N(t)$. Asi pues $N(t)$ es una nueva función vectorial asociada a la curva y esta dada por la ecuación:
\[
N(t)=\frac{T^{\prime}(t)}{\|T^{\prime}(t)\|},\ \ \ \ \text{si} \ \ \|T^{\prime}(t)\| \neq 0
\]
Notese que
$$\|N(t)\|=\left\|\frac{T^{\prime}(t)}{\|T^{\prime}(t)\|}\right\|=1$$
Si en la definición anterior, la curva está parametrizada por
longitud de arco, considerando que $T(s)=\overline{f}'(s)$ , se tiene
$$N(s)=\frac{\overline{f}^{\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|}=\frac{T'(s)}{\|T'(s)\|}$$

Vector Binormal

Un tercer vector definido mediante
$$B(t)=T(t)\times N(t)$$
recibe el nombre de Vector binormal.
Notese que $$\|B(t)\|=\|T(t)\times
N(t)\|=\|T(t)\|\|N(t)\|\sin\left(\frac{\pi}{2}\right)=1$$
En el punto correspondiente a $f(t)$ en la curva, los vectores $T(t)$, $N(t)$ y $B(t)$ conforman un trío de vectores unitarios y mutuamente ortogonales. Estos dan lugar a un sistema de coordenadas llamado sistema de referencia TNB o sistema de referencia de Frenet-Serret de la curva C.
Los vectores $T(t)$, $N(t)$ y $B(t)$ juegan en el punto de la curva correspondiente a $f(t)$ un papel similar al que juega la tríada i, j y k en el origen del espacio tridimensional. Esta última tríada permace fija, en cambio los vectores $T(t)$, $N(t)$ y $B(t)$ conforman una tríada movil que se mueve a lo largo de la curva.

Ejemplo. Dada la curva $r(t)=\cos t \hat{i}+\sin t \hat{j} + t\hat{k}$ cuya parametrización por longitud de arco es
\[
\bar{r}(s)=\left(\cos\left(\frac{s}{\sqrt{2}}\right),\sin\left(\frac{s}{\sqrt{2}}\right),\frac{s}{\sqrt{2}}\right)
\]
Hallar los vectores Tangente, Normal y Binormal en un punto $r(s)$.
Solución.

Vector Tangente
\[
T(s)=\frac{f^{\prime}(s)}{\|f^{\prime}(s)\|}=
\left(
-\frac{1}{\sqrt{2}} \sin\left(\frac{s}{\sqrt{2}}\right),
\frac{1}{\sqrt{2}}\cos \left(\frac{s}{\sqrt{2}}\right),
\frac{1}{\sqrt{2}}
\right)
\]
Vector Normal
\[
N(s)=\frac{T^{\prime}(s)}{\|T^{\prime}(s)\|}=
\left(
-\frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}\right),
-\frac{1}{\sqrt{2}}\left(\frac{1}{\sqrt{2}}\right)\sin\left(\frac{s}{\sqrt{2}}\right),0
\right)
\]
Vector Binormal
\[
B(s)=T(s)\times N(s)=\left|
\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
\frac{-1}{\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\\
-\cos\left(\frac{s}{\sqrt{2}}\right) & -\sin\left(\frac{s}{\sqrt{2}}\right) & 0\\
\end{array}
\right|=
\left(
\frac{1}{\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right),
\frac{-1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right),
\frac{1}{\sqrt{2}}
\right).~~ \blacksquare
\]

Plano Osculador

Sea $f:[a,b]\rightarrow\mathbb{R}^{3}$ una curva con triada móvil $T(t)$, $N(t)$ y $B(t)$. Sea $P=(x_{0},y_{0},z_{0})$ un punto de la curva f tal que $f(t_{0})=(x_{0},y_{0},z_{0})$. Se llama Plano Osculador de f en el punto P, al plano que pasa por P y es paralelo a los vectores $T(t_{0})$ y $N(t_{0})$. Este plano tiene por ecuación
$$\boxed{B(t_{0})\cdot [(x,y,z)-(x_{0},y_{0},z_{0})]=0}$$ El plano osculador es el plano que mejor se adapta a la curva en cada uno de sus puntos. Si la curva es plana, el plano osculador coincide con el plano de la curva.
Ejemplo. Consideremos la curva $f:\mathbb{R}\rightarrow\mathbb{R}^3$ dado por:
\[ f(s)=\left(
\cos\left(\frac{s}{\sqrt{2}}\right),
\sin\left(\frac{s}{\sqrt{2}}\right),
\frac{s}{\sqrt{2}}
\right)
\]
el cual es dos veces diferenciable parametrizado por longitud de arco y que describe una hélice circular en $\mathbb{R}^3$. Obtenga la ecuación del plano osculador en el punto $f(\sqrt{2}\pi)=(-1,0,\pi)$.
Solución.
Tenemos que:
\[ T(s)=\frac{f^{\prime}(s)}{\|f^{\prime}(s)\|}= \left( -\frac{1}{\sqrt{2}} \sin\left(\frac{s}{\sqrt{2}}\right), \frac{1}{\sqrt{2}}\cos \left(\frac{s}{\sqrt{2}}\right), \frac{1}{\sqrt{2}} \right) \]
y $T(\sqrt{2}\pi)=\left(0,-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$, por otro lado:
\begin{align*}N(s)&=\frac{T^{\prime}(s)}{\|T^{\prime}(s)\|}\\&=\left(
-\frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}\right),
-\frac{1}{\sqrt{2}}\left(\frac{1}{\sqrt{2}}\right)\sin\left(\frac{s}{\sqrt{2}}\right),0
\right)\\&=\left(
-\left(\frac{1}{2}\right)\cos\left(\frac{s}{\sqrt{2}},\right),-\left(\frac{1}{2}\right)\sin\left(\frac{s}{\sqrt{2}}\right),0
\right)\end{align*}
y $N(\sqrt{2}\pi)=(1,0,0)$.
Por lo que
\[ T(\sqrt{2}\pi)\times N(\sqrt{2}\ \pi) =\left| \begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ \frac{-1}{\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\\-\left(\frac{1}{2}\right)\cos\left(\frac{s}{\sqrt{2}}\right) & -\left(\frac{1}{2}\right)\sin\left(\frac{s}{\sqrt{2}}\right) & 0\\ \end{array}\right|= \left(\frac{1}{2\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right),\frac{-1}{2\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right),\frac{1}{2\sqrt{2}} \right) \]
al evaluar en $\sqrt{2}\ \pi$ nos queda $\displaystyle{\left(0,\frac{1}{2\sqrt{2}},\frac{1}{2\sqrt{2}}\right)}$. Por lo tanto la ecuación del plano osculador en $P=(-1,0,\pi)$ es: \[ (x+1,y,z-\pi)\cdot\left(0,\frac{1}{2\sqrt{2}},\frac{1}{2\sqrt{2}}\right)=0 \] \[ \Rightarrow \frac{1}{2\sqrt{2}} (y) +\frac{1}{2\sqrt{2}} (z-\pi)=0 \] \[ \Rightarrow y+z=\pi.~~ \blacksquare \]

Plano Normal

Se llama Plano Normal de f en el punto P, al plano que pasa por P y es paralelo a los vectores $N(t_{0})$ y $B(t_{0})$. Este plano tiene por ecuación
$$\boxed{T(t_{0})\cdot [(x,y,z)-(x_{0},y_{0},z_{0})]=0}$$
Ejemplo. Consideremos la curva $f:\mathbb{R}\rightarrow
\mathbb{R}^3$ dado por:
\[ f(t)=\left( 2\cos\left(t\right), 2\sin\left(t\right), t \right) \] el cual es dos veces diferenciable y que describe una hélice circular en $\mathbb{R}^3$. Obtenga la ecuación del plano normal en el punto $f\left(\frac{\pi}{2}\right)=\left(0,2,\frac{\pi}{2}\right)$.
Solución. Tenemos que:
\[ T(t)=\frac{1}{\sqrt{5}}\left(-2\sin(t),2\cos(t),1\right) \] y $\displaystyle{T\left(\frac{\pi}{2}\right)=\frac{1}{\sqrt{5}}\left(-2,0,1\right)}$. Por lo tanto la ecuación del plano normal es: \[ \frac{1}{\sqrt{5}}(-2,0,1)\cdot\left[(x,y,z)-\left(0,2,\frac{\pi}{2}\right)\right]=0 \] \[ \Rightarrow 4x-2z+\pi=0.~~\blacksquare \]

Plano Rectificador

Se llama Plano rectificador de f en el punto P, al plano que pasa por P y es paralelo a los vectores $T(t_{0})$ y $B(t_{0})$. Este plano tiene por ecuación
$$\boxed{N(t_{0})\cdot [(x,y,z)-(x_{0},y_{0},z_{0})]=0}$$
Ejemplo. Consideremos la curva $f:\mathbb{R}\rightarrow \mathbb{R}^3$ dada por:
\[ f(t)=\left( 2\cos\left(t\right), 2\sin\left(t\right), t \right) \] la cual es dos veces diferenciable y que describe una hélice circular en $\mathbb{R}^3$. Obtenga la ecuación del plano rectificador en el punto $\displaystyle{f\left(\frac{\pi}{2}\right)=\left(0,2,\frac{\pi}{2}\right)}$.
Solución. Tenemos que: \[ N(t)=\left(-\cos(t),-\sin(t),0\right) \] y $\displaystyle{N\left(\frac{\pi}{2}\right)=\left(0,-1,0\right)}$. Por lo tanto la ecuación del plano rectificador es: \[ (0,-1,0)\cdot\left[(x,y,z)-\left(0,2,\frac{\pi}{2}\right)\right]=0 \] \[ \Rightarrow y-2=0.~~\blacksquare \]

Mas adelante

En la siguiente entrada veremos como a partir de vectores caracterizados en esta entrada podemos definir y calcular la curvatura y radio de curvatura de una curva o plano.

Tarea Moral

1.- Determina $T$ y $N$ para cada una de las siguientes curvas:

La parábola $x=pt^2$ , $y=2pt$.

La elipse $f(\theta)=(acos\theta, b sen\theta)$, $\theta \in [0,2\pi]$; $a,b>0$

2.- Si una curva está descrita por $f(t)= (t,t^2,t^3)$, determína $T(t)$, $N(t)$, $B(t)$ y el plano osculador cuando $t=0$ y $t=1$

3.- Si $C$ es una curva en $R^3$ descrita por $f$ demuestra que

$B=\dfrac{f’ \times f^{‘ ‘}}{|f’ \times f^{‘ ‘} |}$, $N=B \times T= \dfrac{(f’ \times f^{‘ ‘})\times f’}{| (f’ \times f^{‘ ‘} \times f’)|}$

4.- Demuestra que si una curva $C$ se encuentra en el plano $P$ en $R^3$ entonces el plano osculador en cualquier punto de $C$ es $P$.

5.- Determina $T,N$ y $B$ y el plano osculador en $f(0)$ para las curvas en seguida descritas.

a) $f(t)= (t cost, t sent, t)$

b) $f(t)= (t-sent, 1-cost, t)$

Enlaces

El siguiente interactivo contiene un visualizador de las funciones vectoriales parábola y circunferencia con su vector tangente. Si tienes experiencia con el código puedes implementar cualquier otra función de tu elección.

https://colab.research.google.com/drive/1LIc0KHRJnTz9e-CLPEb9d4KZyr2Vdytq?usp=sharing

Introducción

La longitud de arco es un concepto fundamental del cálculo diferencial e integral que permite medir la distancia real a lo largo de una curva. A diferencia de la geometría elemental, donde solemos trabajar con segmentos rectos, en cálculo nos interesa determinar cuánto “mide” una curva suave, como la gráfica de una función.

Definición. Si C es un arco de curva rectificable, definimos su longitud $L(C)$ como la suma
$$\boxed{L_{C}=\sup{s(P)}=\sup\left\{\Sigma\|f(t_{k})-f(t_{k-1})\|\right\}}$$
Ahora vamos a obtener una fórmula para la longitud de arco.
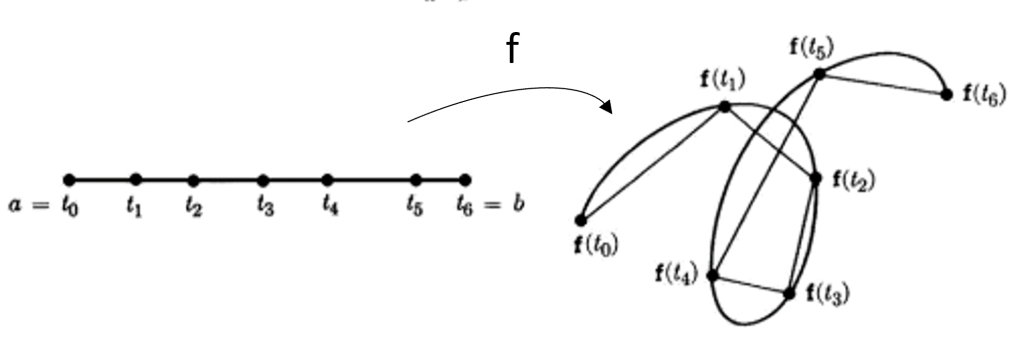
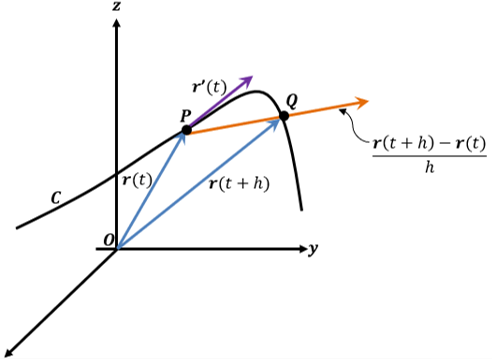
Sea $\overline{\alpha}:[a,b]\rightarrow \mathbb{R}^{2}$ ó $\mathbb{R}^{3}$, continua en $[a,b]$, derivable en (a,b) y $\overline{\alpha^{\prime}}(t)\neq 0$ para todo $t\in [a,b]$ y sea $P={t_{0},t_{1},…,t_{n}}$ una partición de $[a,b]$

entonces según la figura se tiene que
$$\ell(\overline{\alpha})\approx \sum_{i=1}^{n}\|\alpha(t_{i})-\alpha(t_{i-1})\|=\sum_{i=1}^{n}\sqrt{\left[\alpha_{1}(t_{i})-\alpha_{1}(t_{i-1})\right]^{2}+…+\left[\alpha_{n}(t_{i})-\alpha_{n}(t_{i-1})\right]^{2}}$$
Aplicando el teorema del valor medio en cada subintervalo $[t_{i-1},t_{i}]$ tenemos que
$$\frac{\alpha_{i}(t_{i})-\alpha_{i}(t_{i-1})}{t_{i}-t_{i-1}}=\alpha^{\prime}(t^*),~~~t^*\in(t_{i-1},t_{i})$$
se tiene que
\begin{align*}&\sum_{i=1}^{n}\sqrt{\left[\alpha_{1}(t_{i})-\alpha_{1}(t_{i-1})\right]^{2}+…+\left[\alpha_{n}(t_{i})-\alpha_{n}(t_{i-1})\right]^{2}}=\\&\sum_{i=1}^{n}\sqrt{\left[\alpha_{1}^{\prime}(t_{1})(t_{i}-t_{i-1})\right]^{2}+…+\left[\alpha_{n}^{\prime}(t_{n})(t_{i}-t_{i-1})\right]^{2}}=\\&\sum_{i=1}^{n}(t_{i}-t_{i-1})\sqrt{\left[\alpha_{1}^{\prime}(t_{1})\right]^{2}+…+\left[\alpha_{n}^{\prime}(t_{n})\right]^{2}}=\\&\sum_{i=1}^{n}(t_{i}-t_{i-1})\sqrt{\left[\alpha_{1}^{\prime}(t_{1})\right]^{2}+…+\left[\alpha_{n}^{\prime}(t_{n})\right]^{2}}=\\&\sum_{i=1}^{n}(t_{i}-t_{i-1})\sqrt{\left[\alpha_{1}^{\prime}(t)\right]^{2}+…+\left[\alpha_{n}^{\prime}(t)\right]^{2}}=\\&\sum_{i=1}^{n}\|\alpha^{\prime}(t^*)\|(t_{i}-t_{i-1})\\&Si~{n\rightarrow \infty}~~entonces~~\sum_{i=1}^{n}\|\alpha^{\prime}(t^*)\|(t_{i}-t_{i-1})\rightarrow \int_{a}^{b}\|\alpha^{\prime}(t)\|~dt\end{align*}
Definición. Sea $f:I\subset \mathbb{R}\rightarrow \mathbb{R}^{2}$ ó $\mathbb{R}^{3}$ una curva parametrizable. Sean $a,b\in I$ con $a<b$. Para cualquier partición $P={t_{0},…,t_{n}}$ del intervalo $[a,b]$ definimos
$$sup\left\{\sum_{i=1}^{n}\|\alpha^{\prime}(t)\|(t_{i}-t_{i-1})\right\}=\int_{a}^{b}\|\alpha^{\prime}(t)\|~dt$$
curva o la longitud de arco de la curva en caso de que la integral exista.
Ejemplo. Calcular la longitud de arco de $\sigma(t)=(rt-r\sin(t),r-r\cos(t))$. En este caso
tenemos que $\sigma^{\prime}=(r-r\cos(t),r\sin(t))$ para $t\in[0,2\pi]$ $\therefore$ la longitud de arco es:
\begin{align*} \int_{0}^{2\pi}\sqrt{(r-r\cos(t))^{2}+(r\sin(t))^{2}} &=\int_{0}^{2\pi}\sqrt{r^{2}-2r^{2}\cos(t)+r^{2}\cos^{2}(t)+r^{2}\sin^{2}(t)}dt \\ &=\int_{0}^{2\pi}\sqrt{2r^{2}-2r^{2}\cos(t)}dt \\ &=\sqrt{2}r\int_{0}^{2\pi}\sqrt{1-\cos(t)}dt\\ &=\sqrt{2}r\int_{0}^{2\pi}\sqrt{2}\sin\left(\frac{t}{2}\right)dt\\&=2r\int_{0}^{2\pi}\sin\left(\frac{t}{2}\right)dt \\ &=2r\left(2\cdot\left(-\cos\left(\frac{t}{2}\right)\right|_{0}^{2\pi}\right) \\ &=8r.~ \blacksquare \end{align*}

Reparametrización de curvas

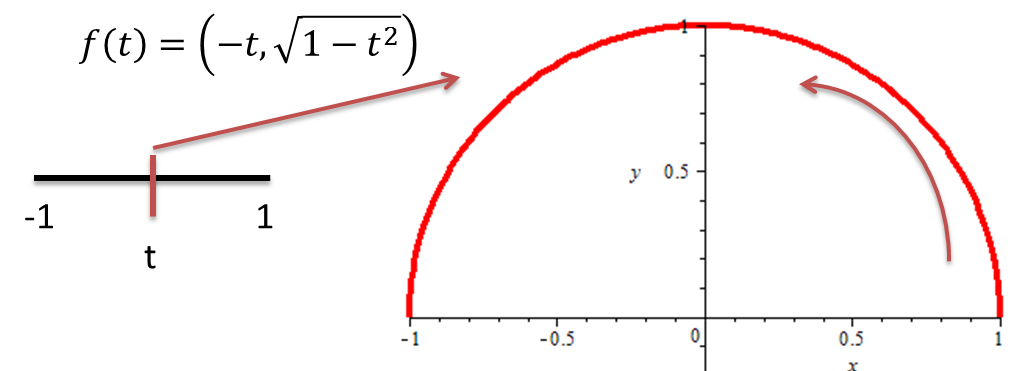
Consideremos la curva $f:[-1,1]\rightarrow \mathbb{R}^{2}$
dada por $f(t)=(-t,\sqrt{1-t^{2}})$ la cual describe un arco de la
circunferencia $x^{2}+y^{2}=1$ entre -1 y 1.

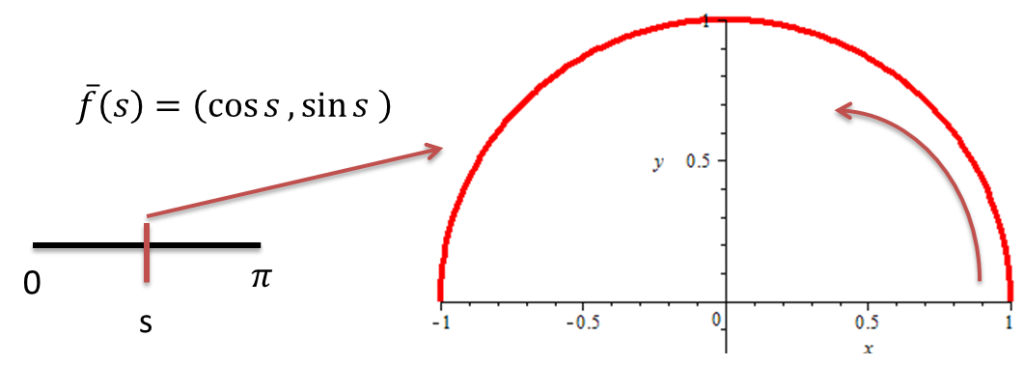
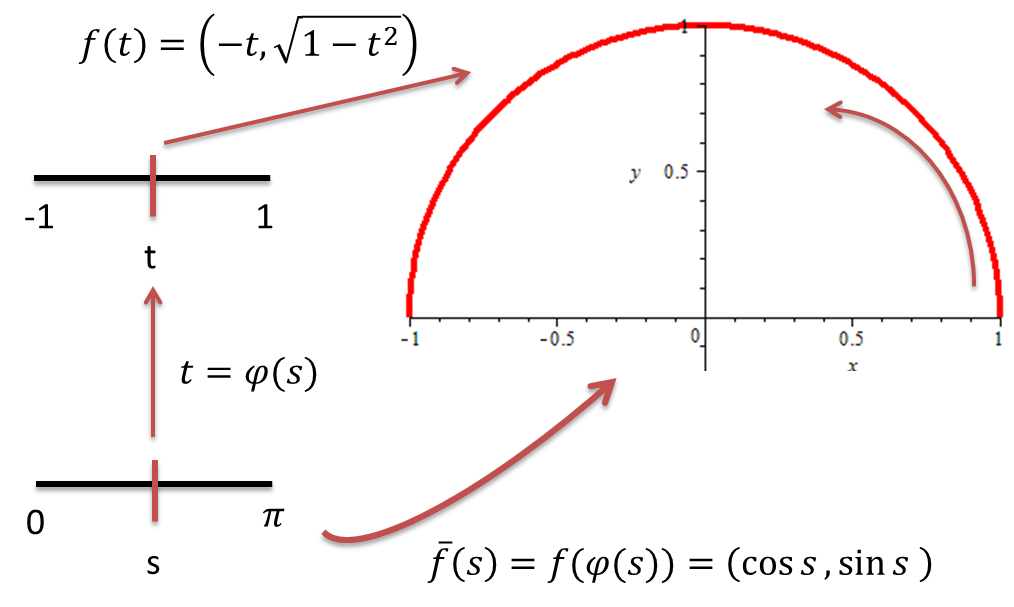
Sea $\overline{f}:[0,\pi]\rightarrow[0,1]$ la función $\overline{f}(s)=[\cos(s),\sin(s)]$

Si definimos una función $\varphi:[0,\pi]\rightarrow[-1,1]$ dada por $\varphi(s)=-cos(s)$ tenemos que $\overline{f}=f\circ\varphi$, es decir
$$\overline{f}(s)=f\circ \varphi(s)=f(\varphi(s))=f(-cos(s))=[-(-cos(s)),\sqrt{1-(-\cos(s))^{2}}]=[cos(s),\sin(s)]$$

Decimos que $\overline{f}$ es una reparametrización de $f$.$~~\blacksquare$
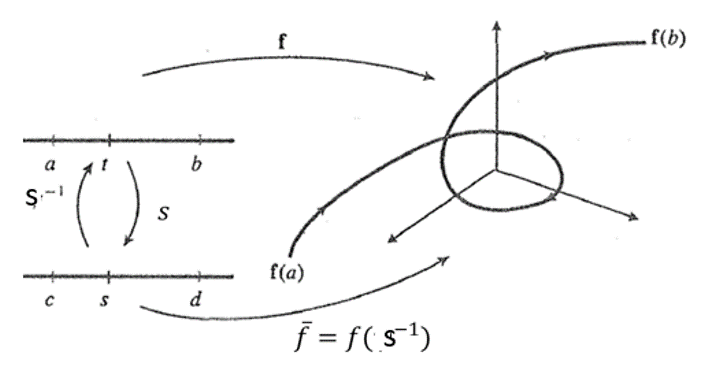
Definición. Sea $f:[a,b]\subset\mathbb{R}^{n}$ una curva con derivada distinta de cero. Sea $\varphi:[c,d]\rightarrow[a,b]$ una función con derivada continua sobreyectiva tal que $\varphi’\neq0$ $\forall s\in [a,b]$. Entonces la curva $\overline{f}=f\circ\varphi:[c,d]\rightarrow\mathbb{R}^{n}$ se llama reparametrización de la curva f.
Nota:
La condición $\varphi’\neq0$ nos conduce a $\varphi’>0$ o $\varphi'<0$. Si $\varphi’>0$ entonces $\varphi$ es una función creciente en [c,d] de modo que $\varphi(c)=a$ y $\varphi(d)=b$ y asi los puntos inicial y final de $\overline{f}$ coinciden con los respectivos de f$$\overline{f}(c)=f\circ\varphi(c)=f(\varphi(c))=f(a)~~~y~~~ \overline{f}(d)=f\circ\varphi(d)=f(\varphi(d))=f(b)$$
como $\overline{f}'(s)=\varphi'(s)f'(\varphi(s))$ entonces $f’$ y $\overline{f}’$ tienen la misma dirección y en este caso como $\varphi’~>0$, entonces, el camino en el que $\overline{f}$ recorre la curva descrita por f es en la misma dirección. Por lo tanto diremos que $\overline{f}$ es una reparametrización de f que conserva la orientación.
Ejemplo. Obtenga una reparametrización de la curva $f:[0,2]\rightarrow\mathbb{R}^{2}$ dada por $f(t)=(3t+2,t^{3}+3)$.
Solución. Proponemos la función $t=\varphi(s)=2s$, en la cual se tiene $\varphi'(s)=2>0$,
es decir si su derivada es constante, entonces no se anula para ningun valor. Ahora bien si $t=0\Rightarrow s=0$ y $t=2\Rightarrow s=1$ por lo tanto $\varphi:[0,1]\rightarrow[0,2]$ mientras que
$$\overline{f}(s)=f(\varphi(s))=f(2s)=(3(2s)+2,(2s)^{3}+3)=(6s+2,8s^{3}+3)\quad
s\in[0,1]$$ tenemos entonces que $\overline{f}$ es una reparametrización de f. Vamos a comprobar que representan el mismo lugar geométrico. Para $f(t)$ se tiene $\displaystyle{x=3t+2\rightarrow t=\frac{x-2}{3}}$ y si $y=t^{3}+3$ entonces $\displaystyle{y=\left(\frac{x-2}{3}\right)^{3}+3}$ mientras que para $\overline{f}(s)$, $\displaystyle{x=6s+2\rightarrow s=\frac{x-2}{6}}$ por tanto si $y=8s^{3}+3$ entonces $\displaystyle{y=8\left(\frac{x-2}{6}\right)^{3}+3}$ por lo que igualando coordenadas de cada representación paramétrica, se tiene$$\left(\frac{x-2}{3}\right)^{3}+3=8\left(\frac{x-2}{6}\right)^{3}+3\Rightarrow \frac{1}{3^{3}}=\frac{8}{6^{3}}$$ lo cual es cierto y por lo tanto representan el mismo lugar geometrico.$~~\blacksquare$
Proposición. Supongamos que $f:[a,b]\rightarrow\mathbb{R}^{n}$ es una curva con $f’\neq 0$ y que $\overline{f}:[c,d]\rightarrow\mathbb{R}^{n}$ es una reparametrización de f. Entonces
$$\int_{a}^{b}\|f'(t)\|~dt=\int_{c}^{d}\|\overline{f}'(s)\|~ds$$
Demostración. Tenemos que $\overline{f}=f\circ \varphi$, donde $\varphi:[c,d]\rightarrow[a,b]$ es de clase $c^{1}$, biyectiva y $\varphi’\neq 0~~\forall~s\in [c,d]$. Entonces
\begin{align*} L(\overline{f}) &=\int_{c}^{d}|\overline{f}'(s)|~ds \\ &=\int_{c}^{d}\|\varphi'(s)f'(\varphi(s))\|~ds \\ &=\int_{c}^{d}\|\overline{f}'(\varphi(s))\|~|\varphi'(s)|~ds~~~(si~\varphi’>0)\\
&=\int_{c}^{d}\|\overline{f}'(\varphi(s))\|~\varphi'(s)~ds \\
&=\int_{a}^{b}\|f'(t)\|~dt,~~(t=\varphi(s),~~dt=\varphi'(s)~ds) \\
&=L(f).~~ \blacksquare \end{align*}

Función Longitud de Arco

A continuación introducimos la función longitud de arco de una curva. Esta función nos permitirá prporcionar una nueva reparametrización de una curva, lo cual será de gran
utilidad más adelante.
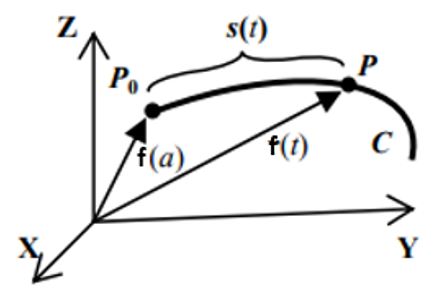
Definición. Sea $f:[a,b]\rightarrow\mathbb{R}^{n}$ una curva de longitud L. Se llama función longitud de arco de la curva $f(t)$ a la función $s:[a,b]\rightarrow[0,L]$ dada por
$$s(t)=\int_{a}^{t}\|f'(u)\|~du$$
$s(t)$ es la longitud del arco entre los puntos $P_{0}$ y $P$, que son los puntos terminales de $f(a)$ y $f(t)$

Ejemplo. Hallar la función longitud de arco de la hélice $f(t)=(\cos(t),\sin(t),t),~~t\in[0,2\pi]$.
Solución. En este caso tenemos que
\begin{align*} f'(t) & =(-\sin(t),\cos(t),1) \\ |f'(t)| & =\sqrt{(-\sin(t))^{2}+(\cos(t))^{2}+1^{2}}=\sqrt{2} \end{align*}
Ahora, para $t\in[0,2\pi]$ tenemos
$$s(t)=\int_{0}^{t}\|f'(u)\|~du=\int_{0}^{t}\sqrt{2}~du=\sqrt{2}t$$
Si $t\in[0,2\pi]$ entonces
\begin{align*} s(0)&=0\\s(2\pi)&=2\pi\sqrt{2}\end{align*}
Luego, la función longitud de arco $s:[0,2\pi]\rightarrow[0,2\pi\sqrt{2}]$ de esta porción de hélice es
$$s(t)=\sqrt{2}t.~~ \blacksquare$$

Reparametrización por Longitud de Arco

Entre las muchas reparametrizaciones de una curva contamos con una que está muy relacionada con las características geométricas de la curva y además, posee propiedades importantes. Esta es la reparametrización por longitud de arco, la que se obtiene mediante la función de longitud de arco.
Sea $f:[a,b]\rightarrow\mathbb{R}^{n}$ una curva diferenciable. Para reparametrizarla por longitud de arco se siguen los siguientes pasos:
(a) Hallar la función longitud de arco de la curva:
$$s:[a,b]\rightarrow[0,L],~~~\displaystyle{s(t)=\int_{a}^{t}\|f'(u)\|~du}$$
(b) Hallar la función inversa de la función longitud de arco:
$$\varphi=s^{-1}:[0,L]\rightarrow[a,b]$$
La reparametrización por longitud de arco de la curva $f:[a,b]\rightarrow\mathbb{R}^{n}$ es
$$\overline{f}=f\circ \varphi:[0,L]\rightarrow\mathbb{R}^{n}$$
Ejemplo. Sea $f(t)=(r \cos t , r\sin t)$ con $t\in[0,2\pi]$. Obtengamos su reparametrizacion por longitud de arco.
Solución.
(a) Hallamos la función longitud de arco s(t) que en éste caso es:
$$f'(t)=(-r\sin(t),r\cos(t))~~y~~\|f'(t)\|=\sqrt{(-r\sin(t))^{2}+(r\cos(t))^{2}}=r$$
$s:[0,2\pi]\rightarrow[0,2\pi r]$, $\displaystyle{s(t)=\int_{0}^{t}\|f'(u)\|~du=\int_{0}^{t}r~du=rt}$ esto es
$$s(t)=rt$$
Si $t\in[0,2\pi]$ entonces
\begin{align*}s(0)&=0\\s(2\pi)&=2\pi r\end{align*}
Por lo que $s\in[0,2\pi r]$
(b) Hallamos la función inversa de la longitud de arco
$$\varphi=s^{-1}:[0,2\pi r]\rightarrow[0,2\pi]$$
Sea $s=s(t)$. Entonces $s=rt$, por lo tanto despejando t tenemos $\displaystyle{t=\frac{s}{r}}$. Luego
$$t=\varphi(s)=s^{-1}=\frac{s}{r}$$
Por lo tanto la reparametrización buscada es
$$\overline{f}(s)=f\circ \varphi(s)=f\left(\varphi(s)\right)=f\left(\frac{s}{r}\right)=\left(r\cos
\left(\frac{s}{r}\right),r\sin\left(\frac{s}{r}\right)\right)~~\blacksquare$$
Observación.
En el ejemplo anterior notamos que:
$$\|\overline{f}^{\prime}(s)\|=
\left\|-r\sin\left(\frac{s}{r}\right)\frac{1}{r},r\cos \left(\frac{s}{r}\right)\frac{1}{r}\right\|=
\left\|-\sin\left(\frac{s}{r}\right),\cos\left(\frac{s}{r}\right)\right\|=1$$

Ejemplo. Sea $f(t)=(\cos t , \sin t,t),~~t\in[0,2\pi]$ . Obtengamos la reparametrizacion por la longitud de arco.
Solución.
(a) Hallamos la función longitud de arco s(t), que en éste caso es:
$$f'(t)=(-\sin(t),\cos(t),1)~~y~~\|f'(t)\|=\sqrt{(\sin(t))^{2}+(\cos(t))^{2}+1^{2}}=\sqrt{2}$$
Si $t\in[0,2\pi]$ entonces $s:[0,2\pi]\rightarrow[0,2\pi \sqrt{2}]$, por lo que$\displaystyle{s(t)=\int_{0}^{t}\|f'(u)\|~du=\int_{0}^{t}\sqrt{2}~du=\sqrt{2}t}$ esto es
$$s(t)=\sqrt{2}t$$
Hallamos la función inversa de la longitud de arco
$$\varphi=s^{-1}:[0,2\pi \sqrt{2}]\rightarrow[0,2\pi]$$
Sea $s=s(t)$. Entonces $s=\sqrt{2}t$, por lo tanto despejando t tenemos $\displaystyle{t=\frac{s}{\sqrt{2}}}$. Luego
$$t=\varphi(s)=s^{-1}=\frac{s}{\sqrt{2}}$$
y la reparametrización buscada es
$$\overline{f}(s)=f\circ h(s)=f\left(h(s)\right)=f\left(\frac{s}{\sqrt{2}}\right)=\left(r\cos
\left(\frac{s}{\sqrt{2}}\right),\sin\left(\frac{s}{\sqrt{2}}\right),\frac{s}{\sqrt{2}}\right),~~s\in[0,2\pi \sqrt{2}] \blacksquare$$

La reparametrización por longitud de arco tiene rapidez constante

Sabemos que si $\textbf{s}:[a,b]\rightarrow [c,d]$ es una función de clase $c^{1}$ tal que $\textbf{s}’\neq 0~~\forall~t\in[a,b]$, también se tiene $\textbf{s}^{-1}:[c,d]\rightarrow [a,b]$ es tal que $(\textbf{s}^{-1})’$ es de clase $c^{1}$.
Observamos que la función $\varphi=\textbf{s}^{-1}:[c,d]\rightarrow [a,b]$ tiene entonces las características que se necesitan para que $\overline{f}=f\circ \varphi$ sea una reparametrización de f.

Tenemos que para $s\in [c,d]$
$$\overline{f}(s)=(f\circ\varphi)(s)=f(\varphi(s))$$
por lo que
$$\overline{f}'(s)=(f\circ\varphi)'(s)=f'(\varphi(s))\varphi'(s)$$
Pero
$$\varphi'(s)=(\textbf{s}^{-1})'(s)=\frac{1}{\textbf{s}'(\textbf{s}^{-1}(s))}=\frac{1}{\textbf{s}'(\varphi(s))}=\frac{1}{\|f'(\varphi(s))\|}$$
Por lo tanto
$$\|\overline{f}'(s)\|=\|f'(\varphi(s))\varphi'(s)\|=\left\|f'(\varphi(s))\cdot\frac{1}{\|f'(\varphi(s))\|} \right\|=\|f'(\varphi(s))\|\cdot\frac{1}{\|f'(\varphi(s))\|}=1~~ \blacksquare$$

Propiedad de la reparametrización por longitud constante

Si $\overline{f}$ es una reparametrización de f tal que $\|\overline{f}(t)\|=1$ para toda $t\in [a,b]$ entonces
$$L(\overline{f})=\int_{a}^{b}\|\overline{f}(t)\|~dt=\int_{a}^{b}~dt=b-a$$
Por lo que $\overline{f}$ es una reparametrización tal que la longitud que describe es igual al tiempo que tarda en recorrerla.$~\blacksquare$

Más adelante

El estudio de la longitud de arco no es un tema aislado, sino la base conceptual que permite pasar de una visión métrica (medición de la curva) a una visión geométrica más profunda (entender cómo se orienta y cómo se curva en el espacio). La transición hacia los vectores tangente, normal y binormal representa un avance natural desde el cálculo integral hacia la geometría diferencial de curvas.

Tarea Moral

1.- Aporta una parametrización al cuadrado unitario de $\mathbb{R}^2$ con vértices en los puntos: (0,0), (1,0), (1,1), (0,1).

2.- Determina la longitud de arco de la parábola descrita por $f(t)=(t^2,2t)$, $t\in [0,1]$

3.- Determina la longitud de la gráfica de $y=ln(1-x^2)$ entre $x=0$ y $x=\dfrac{1}{2}$

4.- La gráfica polar de $r=1+cos\theta$ es una cardioide y sus ecuaciones paramétricas son: $x=(1+cos\theta)cos\theta$, $y=(1+cos\theta) sen\theta $, $\theta \in [0,2\pi]$. Determina su longitud de arco.

5.- Encuentra una reparametrización de la elipse $r(t)=(acost, bsent)$, $t\in [0,2\pi]$ y determina su reparametrización por longitud de arco.

Enlaces

La siguiente liga de google colab presenta una calculadora de integral para determinar si una curva es rectificable en el lenguaje de programación R. Es importante mencionar que el código hace el cálculo numérico no teórico, es decir, puede haber falla para integrales impropias o en singularidades.

También puedes comprobar tus resultados de los ejercicios de la tarea moral.

https://colab.research.google.com/drive/1zBwwwivmvw-6gnUXbz6XETgESPFi0VEU?usp=sharing