Introducción

La longitud de una curva como una integral nos permite estudiarla analíticamente. Recordemos que en cálculo el estudio de ciertos objetos matemáticos se hacen a partir de una aproximación. En este caso la noción intuitiva será: la longitud de una curva será el límite de longitudes de polígonos aproximados. Esta longitud estará definida como una integral.

Definición. Una arco de curva esta dado por una función vectorial $f:[a,b]\rightarrow\mathbb{R}^{n}$. Donde el dominio esta restringido al intervalo cerrado $[a,b]\in\mathbb{R}$.
Definición. Sea C un arco de curva en $\mathbb{R}^{n}$ dada por la función
$$f(t)=(f_{1}(t),f_{2}(t),…,f_{n}(t))$$
Consideremos el conjunto
$$P=\{P~\Big{|}~P~es~partici\acute{o}n~de~[a,b]\}$$
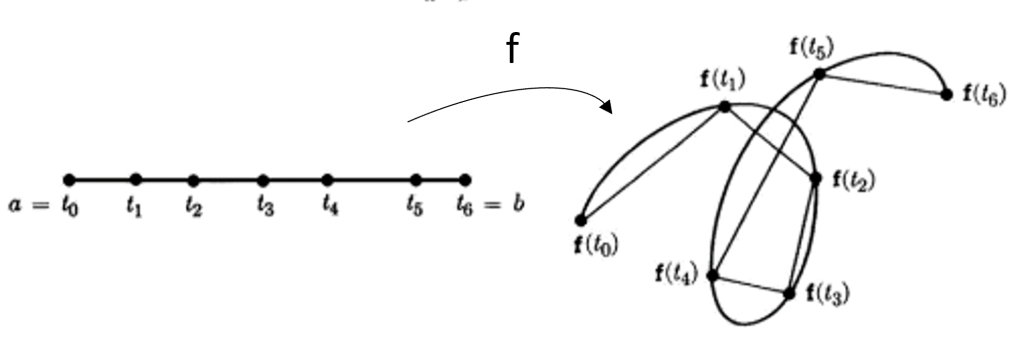
Para cada partición $P:~a=t_{0},t_{1},…,t_{n-1},t_{n}=b$ de $[a,b]$ consideramos la poligonal
$$f(t_{0}),f(t_{2}),…,f(t_{n-1}),f(t_{n})$$
y su correspondiente longitud
$$s(P)=|f(t_{1})-f(t_{0})|+|f(t_{2})-f(t_{1})|+\cdots+|f(t_{n-1})-f(t_{n})|=\sum_{i=1}^{n}||f(t_{i})-f(t_{i-1})||$$
Se dice C es rectificable si el conjunto ${s(P)}$ esta acotado.

Ejemplo. Muestre que el arco de parábola C dado por $f(t)=(t,t^{2})$ con $t\in(0,1)$ es rectificable.
En este caso sea $P\in[0,1]$ dada por $0=t_{0}<t_{1}<\cdots<t_{n}=1$. Tenemos entonces
\begin{align*} s(P) & =\sum_{i=1}^{n}|f(t_{i})-f(t_{i-1})| \\ & =\sum_{i=1}^{n}|(t_{i},t_{i}^{2})-(t_{i-1},t_{i-1}^{2})| \\ &=\sum_{i=1}^{n}|(t_{i}-t_{i-1},t_{i}^{2}-t_{i-1}^{2})| \\ & \leq \sum_{i=1}^{n}|t_{i}-t_{i-1}|+|t_{i}^{2}-t_{i-1}^{2}| \\ &=\sum_{i=1}^{n}|t_{i}-t_{i-1}|+|(t_{i}-t_{i-1}|~|(t_{i}+t_{i-1}|\\ &=\sum_{i=1}^{n}(t_{i}-t_{i-1})(1+(t_{i}-t_{i-1})~~\textcolor{red}{Si~0\leq t_{i-1}\leq t_{1}\leq 1~entonces~1+t_{i-1}+t_{i}\leq 3}\\ &\leq 3\sum_{i=1}^{n}(t_{i}-t_{i-1})\\ &\leq 3 \end{align*}
esto quiere decir que la suma $s(P)$ es acotada y por lo tanto, el arco es rectificable.$~~ \blacksquare$
Ejemplo. Mostrar que la siguiente función vectorial (curva) $f:[0,1]\rightarrow\mathbb{R}^{2}$ dada por $\displaystyle{f(t)=\left[t,t\cos\left(\frac{1}{t}\right)\right]}$ donde $f(0)=(0,0)$ no es rectificable.
En este caso consideramos particiones de $[0,1]$ de la forma
$$P:t_{0}=0,t_{1}=\frac{1}{(n-1)\pi},t_{2}=\frac{1}{(n-2)\pi},…,t_{n-2}=\frac{1}{2\pi},t_{n-1}\frac{1}{\pi},t_{n}=1$$
Los puntos de la poligonal que corresponden a la partición P son
$$f(t_{0})=(0,0),f(t_{1})=\left(\frac{1}{(n-1)\pi},\frac{1}{(n-1)\pi}\cos((n-1)\pi)\right),f(t_{2})=\left(\frac{1}{(n-2)\pi},\frac{1}{(n-2)\pi}\cos((n-2)\pi)\right),…$$
$$,f(t_{n-2})=\left(\frac{1}{2\pi},\frac{1}{2\pi}\cos(2\pi)\right),f(t_{n-1})=\left(\frac{1}{\pi},\frac{1}{\pi}\cos(\pi)\right),f(t_{n})=(1,\cos(1))$$
La suma de las distancias de los segmentos de la poligonal es
\begin{align*} s(P)&=|f(t_{1})-f(t_{0})|+|f(t_{2})-f(t_{1})|+\cdots|f(t_{n})-f(t_{n-1})| \\ &=\left|\left(\frac{1}{(n-1)\pi},\frac{1}{(n-1)\pi}\cos((n-1)\pi)\right)\right| \\ &+\left|\left(\frac{1}{(n-2)\pi}-\frac{1}{(n-1)\pi},\frac{1}{(n-2)\pi}\cos((n-2)\pi)-\frac{1}{(n-1)\pi}\cos((n-1)\pi)\right)\right| \\ &+\cdots+\left|\left(1-\frac{1}{\pi},\cos(1)-\frac{1}{\pi}\cos(\pi)\right)\right| \\ &\geq \sum_{k=1}^{n-2}\left|\left(\frac{1}{k\pi}-\frac{1}{(k+1)\pi},\frac{1}{k\pi}\cos(k\pi)-\frac{1}{(k+1)\pi}\cos((k+1)\pi)\right)\right| \\ &\geq \sum_{k=1}^{n-2}\left|\frac{1}{k\pi}\cos(k\pi)-\frac{1}{(k+1)\pi}\cos((k+1)\pi)\right|\\ &\geq \sum_{k=1}^{n-2}\left|\frac{(-1)^{k}}{k\pi}-\frac{(-1)^{k+1}}{(k+1)\pi}\right|\\ &=\sum_{k=1}^{n-2}\left|\frac{1}{k\pi}+\frac{1}{(k+1)\pi}\right|\\ &\geq \frac{2}{\pi}\sum_{k=1}^{n-2}\frac{1}{k+1} \end{align*}
Entonces,
$$\lim_{n\rightarrow\infty}s(P)\geq \lim_{n\rightarrow\infty}\frac{2}{\pi}\sum_{k=1}^{n-2}\frac{1}{k+1}=+\infty$$
lo cual implica que la suma $s(P)$ no es acotada y por lo tanto el arco de curva no es rectificable.$~~ \blacksquare$
Teorema. [Criterio para determinar si una curva es rectificable]
Todo arco de curva de clase $C^{1}$ (con derivada continua) es rectificable.
Demostración.Sea $f(t)=(f_{1}(t),f_{2}(t),…,f_{n}(t))$ un arco de curva de clase $C^{1}$. Entonces, las funciones $f'{i}$ son continuas en $[a,b]$ y por tanto estan acotadas es decir, existen constantes positivas $M{1},…,M_{n}$ tales que
$$|f'{1}(t)|\leq M{1},…,|f'{n}(t)|\leq M{n}~~~\forall~t\in[a,b]$$
Sea P una partición del intervalo $[a,b]$ determinada por los puntos $a=t_{0}<t_{1}<\cdots<t_{n}=b$. Para cada $i\in{1,2,…,n}$ tenemos
\begin{align*} \|f(t_{i})-f(t_{i-1})\|&=\sqrt{\sum_{j=1}^{n}\left(f_{j}(t_{i})-f_{j}(t_{i-1})\right)^{2}} \\ &\leq \sum_{j=1}^{n}\left|f_{j}(t_{i})-f_{j}(t_{i-1})\right| \end{align*}
Por el teorema del valor medio de Lagrange, existen $\xi_{1},\xi_{2},…,\xi_{n}$ en el intervalo $(t_{i-1},t_{i})$ tales que
\begin{align*} \left|f_{1}(t_{i})-f_{1}(t_{i-1})\right| &= |f'{1}(\xi{1})|(t_{i}-t_{i-1}) \\
\vdots & =\vdots \\
\left|f_{n}(t_{i})-f_{n}(t_{i-1})\right| &= |f'{n}(\xi{1})|(t_{i}-t_{i-1})
\end{align*}
En consecuencia,
\begin{align*} \|f(t_{i})-f(t_{i-1})\|&\leq \left|f_{1}(t_{i})-f_{1}(t_{i-1})\right|+\cdots +\left|f_{n}(t_{i})-f_{n}(t_{i-1})\right| \\ & \leq \left(|f'{1}(\xi{1})|+\cdots+|f'{n}(\xi{1})|\right)(t_{i}-t_{i-1})\\
&\leq (M_{1}+\cdots+ M_{n})(t_{i}-t_{i-1}).
\end{align*}
Si $s(P)$ es la longitud de la poligonal determinada por P tenemos
\begin{align*} s(P)&=\sum_{i=1}^{n}\|f(t_{i})-f(t_{i-1})\| \\ &\leq (M_{1}+\cdots+ M_{n})\sum_{i=1}^{n}(t_{i}-t_{i-1}) \\ &=(M_{1}+\cdots+ M_{n})(b-a). \end{align*}
Es decir, el conjunto ${s(P)}$ con P partición de $[a,b]$ está acotado y por tanto el arco de curva es rectificable.$ \blacksquare$
Ejemplo. Muestre que el arco de curva C dado por $f(t)=(t,t^{3})$ con $t\in(0,1)$ es rectificable.
En este caso $f'(t)=(1,3t^{2})$, cada función componente es continua y por tanto $f(t)$ es de clase $C^{1}$ por lo que según el resultado anterior, se tiene que f es rectificable en el intervalo indicado.$~~\blacksquare$

Más adelante

En esta sección vimos cómo aproximar la longitud de arco de una función vectorial con dominio acotado mediante el cálculo de las longitudes de polígonos. En la siguiente sección definiremos el cálculo de la longitud de arco, el cual, está determinado mediante una integral.

Tarea Moral

1.- Prueba que la curva definida como $y=\begin{cases}x^{2}sen\dfrac{1}{x},0< x\leq 1\\ 0,x=0\end{cases}$ tiene longitud finita.

2.- Prueba que $y=\begin{cases}xsen\dfrac{1}{x},0< x\leq 1\\ 0,x=0\end{cases}$ no es rectificable.

3.- Prueba que si una función f es deinida y monótona en el intervalo cerrado $[a,b]$ entonces el arco de curva definido como $y=f(x)$, $(a\leq x \leq b)$ es rectificable.

4.- Muestra que la siguiente función $\gamma :A=\left[ 0,2\pi \right] \rightarrow \mathbb{R}$ dada por $\gamma(t)=\dfrac{3}{2}(cos(t), sint(t))$ es rectificable.

5.- Propón una función vectorial cuyo arco de curva sea rectificable y una donde no lo sea.