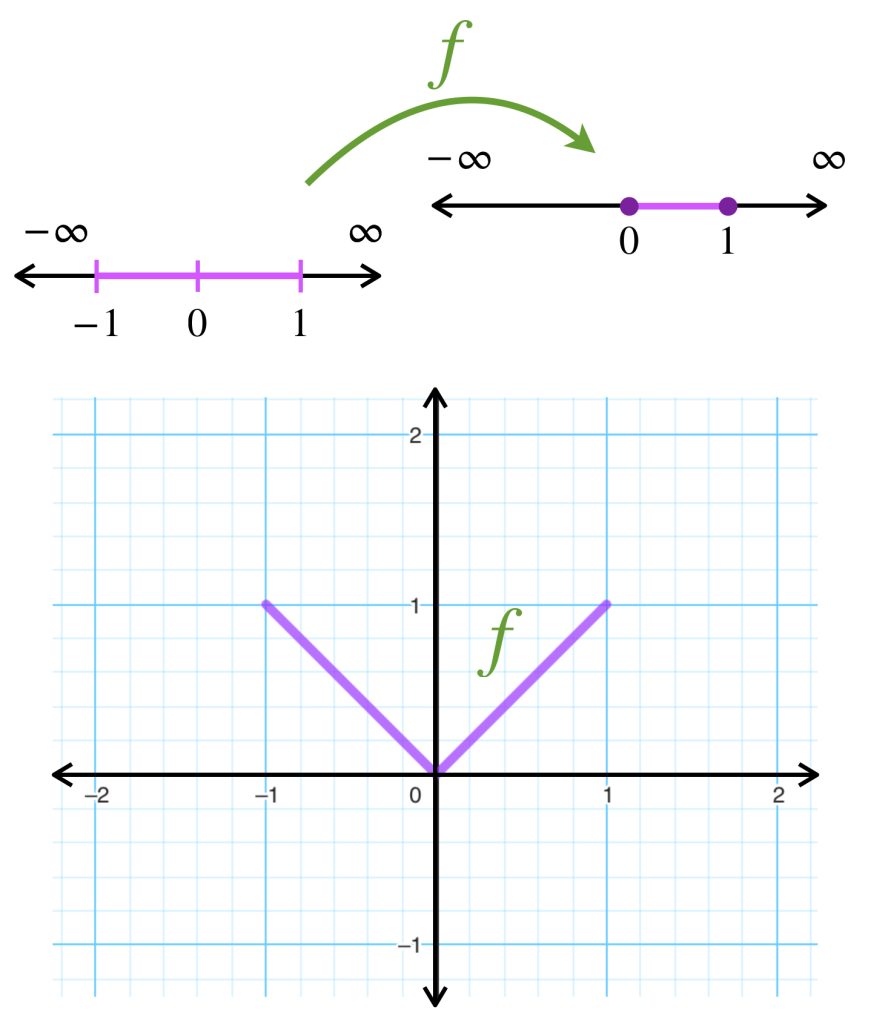
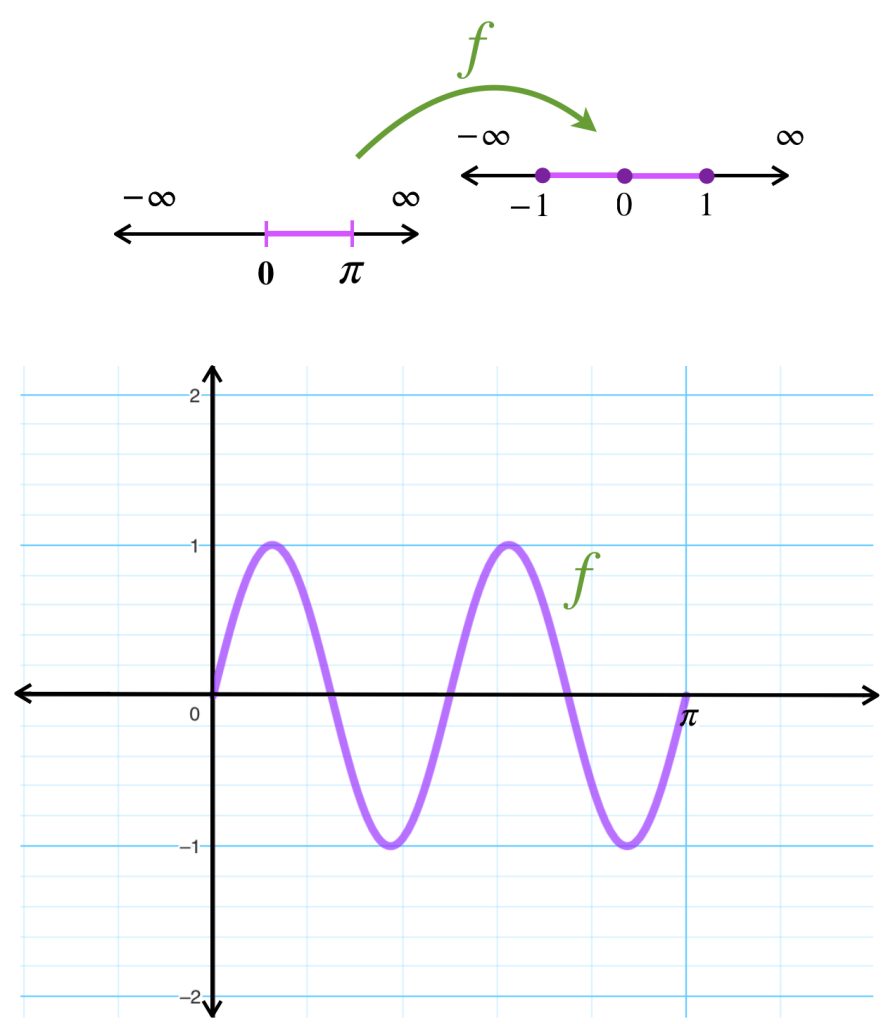
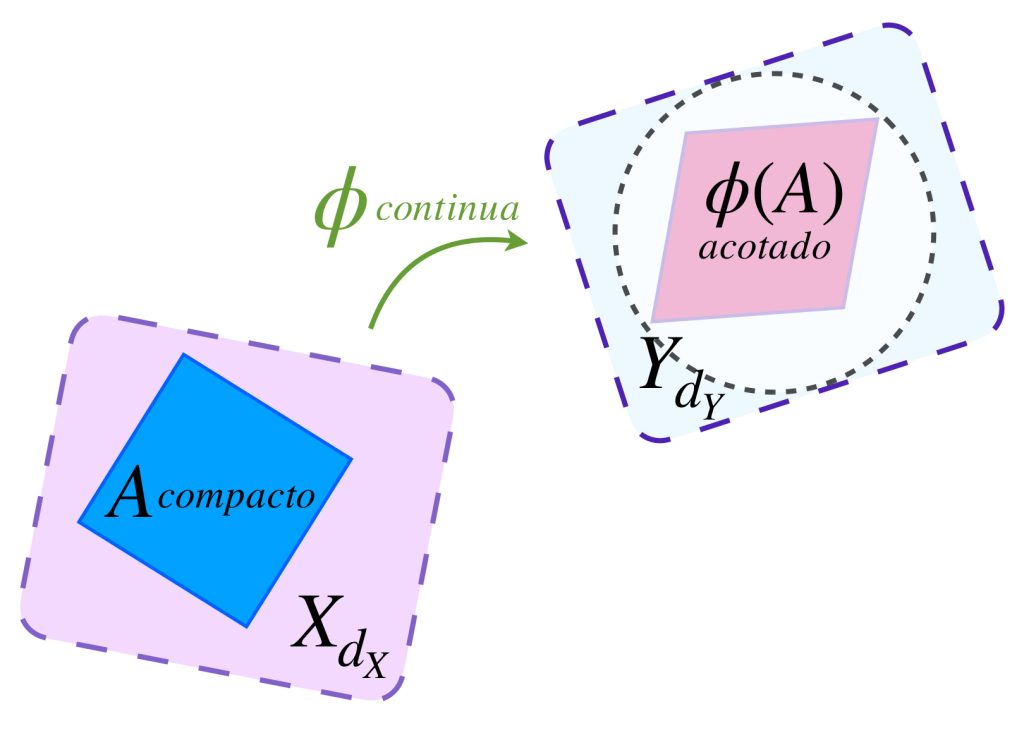
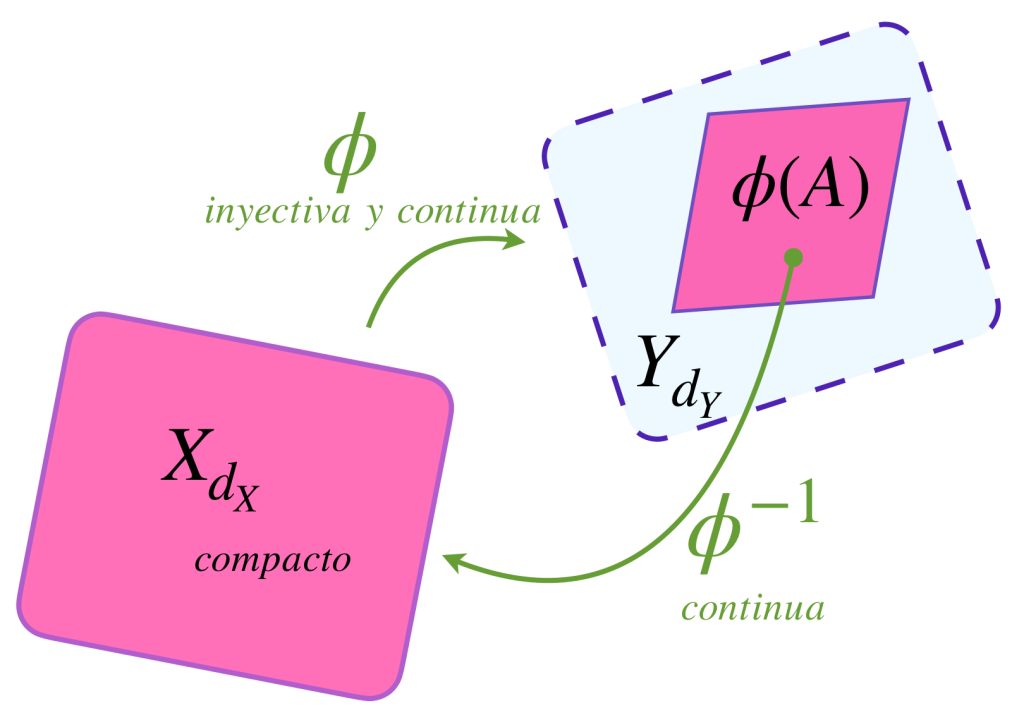
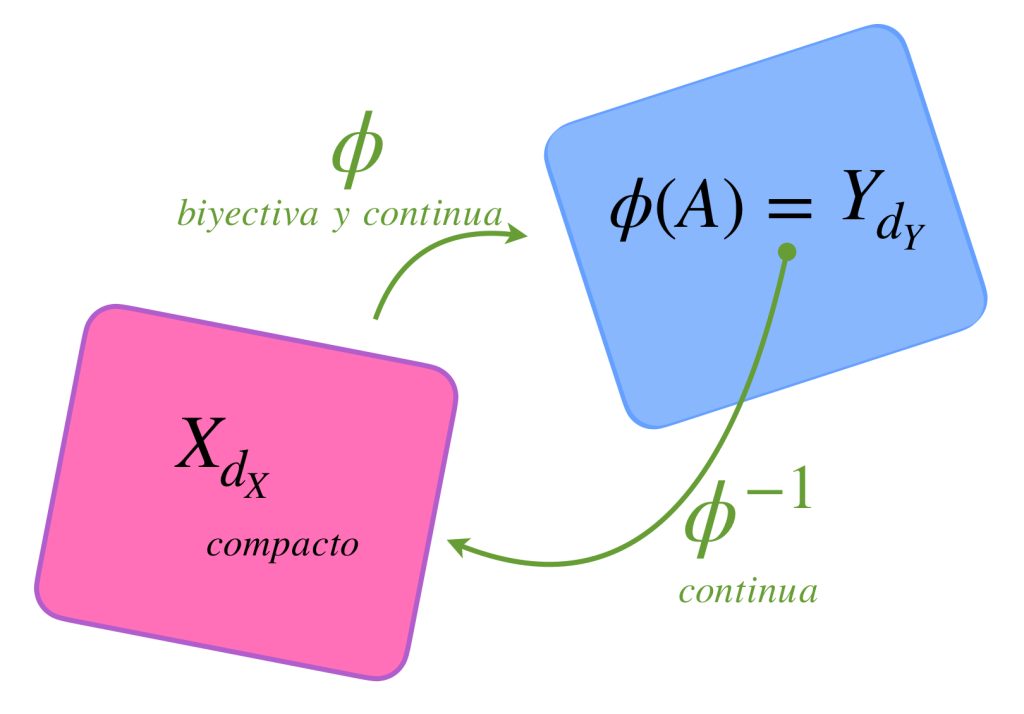
Introducción

Teorema de la Función Implícita (sistemas de ecuaciones

Teorema 1. Considere las funciones $z_{1}=F(x,y,u,v)$ y $z_{2}=G(x,y,u,v)$. Sea $P=(x,y,u,v) \in \mathbb{R}^{4}$ un punto tal que $F(P)=G(P)=0$. Suponga que en una bola $\textit{B} \in \mathbb{R}^{4}$ de centro $P$ las funciones $F$ y $G$ tienen (sus cuatro) derivadas parciales continuas. Si el Jacobiano $\displaystyle \frac{\partial
(F,G)}{\partial (u,v)}(P)\neq0$ entonces las expresiones $F(x,y,u,v)=0$ y $G(x,y,u,v)=0$ definen funciones (implícitas) $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ definidas en una vecindad $v$ de $(x,y)$ las cuales tienen derivadas parciales continuas en $v$

Dadas las funciones $F$ y $G$ de las variables $u,v,x,y$ nos preguntamos cuando de las expresiones

$F(x,y,u,v)=0$
$G(x,y,u,v)=0$

podemos despejar a $u$ y $v$ en términos de $x$ y $y$ en caso de ser posible diremos que las funciones $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ son funciones implícitas dadas. Se espera que $\exists’$n funciones $u=\varphi_{1}(x,y)$ y
$v=\varphi_{2}(x,y)$ en

$F(x,y,\varphi_{1}(x,y),\varphi_{2}(x,y)$
$G(x,y,\varphi_{1}(x,y),\varphi_{2}(x,y)$

con $(x,y)$ en alguna vecindad $V$

Suponiendo que existen $\varphi_{1}$ y $\varphi_{2}$ veamos sus derivadas

$\displaystyle \frac{\partial F}{\partial x}\displaystyle \frac{\partial x}{\partial x}+\displaystyle \frac{\partial F}{\partial y}\displaystyle \frac{\partial y}{\partial x}+\displaystyle \frac{\partial F}{\partial u}\displaystyle \frac{\partial u}{\partial
x}+\displaystyle \frac{\partial F}{\partial v}\displaystyle \frac{\partial v}{\partial x}=0$ $~~$ $\Rightarrow$ $~~$ $\displaystyle \frac{\partial F}{\partial u}\displaystyle
\frac{\partial u}{\partial x}+\displaystyle \frac{\partial F}{\partial v}\displaystyle \frac{\partial v}{\partial x}=-\displaystyle \frac{\partial F}{\partial x}$

$\displaystyle \frac{\partial G}{\partial x}\displaystyle \frac{\partial x}{\partial x}+\displaystyle \frac{\partial G}{\partial y}\displaystyle \frac{\partial y}{\partial
x}+\displaystyle \frac{\partial G}{\partial u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial G}{\partial v}\displaystyle \frac{\partial v}{\partial x}=0$ $~~$ $\Rightarrow$ $~~$ $\displaystyle \frac{\partial G}{\partial u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial G}{\partial v}\displaystyle \frac{\partial v}{\partial x}=-\displaystyle \frac{\partial G}{\partial x}$

Lo anterior se puede ver como un sistema de 2 ecuaciones con 2 incógnitas $\displaystyle \frac{\partial u}{\partial x}$ y $\displaystyle \frac{\partial v}{\partial x}$. Aquí se ve que para que el sistema tenga solución.

$det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|\neq0$ en $(P)$ (el $det$ Jacobiano) y según la regla de Cramer

$\displaystyle \frac{\partial u}{\partial x}=\frac{\det
\left|\begin{array}{cc} \displaystyle -\frac{\partial F}{\partial
x}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle -\frac{\partial G}{\partial x}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}{\det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}=-\frac{\frac{\partial (F,G)}{\partial(x,v)}}{\frac{\partial(F,G)}{\partial(u,v)}}$, $\displaystyle \frac{\partial
v}{\partial x}=\frac{\det \left|\begin{array}{cc} \displaystyle
\frac{\partial F}{\partial u}&\displaystyle -\frac{\partial
F}{\partial x}
\\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle -\frac{\partial G}{\partial
x}\end{array}\right|}{det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}=-\frac{\frac{\partial (F,G)}{\partial(u,x)}}{\frac{\partial(F,G)}{\partial(u,v)}}$.

Análogamente si derivamos con respecto a $y$ obtenemos

$\displaystyle \frac{\partial F}{\partial u}\displaystyle \frac{\partial u}{\partial y}+\displaystyle \frac{\partial F}{\partial v}\displaystyle \frac{\partial v}{\partial y}=\displaystyle \frac{\partial F}{\partial y}$

$\displaystyle \frac{\partial G}{\partial
u}\displaystyle \frac{\partial u}{\partial y}+\displaystyle
\frac{\partial G}{\partial v}\displaystyle \frac{\partial
v}{\partial y}=\displaystyle \frac{\partial G}{\partial y}$

de donde

$\displaystyle \frac{\partial u}{\partial y}=-\frac{\det
\left|\begin{array}{cc} \displaystyle -\frac{\partial F}{\partial
y}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle -\frac{\partial G}{\partial y}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}{det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}=-\frac{\frac{\partial (F,G)}{\partial(y,v)}}{\frac{\partial(F,G)}{\partial(u,v)}}$, $\displaystyle \frac{\partial
v}{\partial y}=-\frac{\det \left|\begin{array}{cc} \displaystyle
\frac{\partial F}{\partial u}&\displaystyle -\frac{\partial
F}{\partial y}
\\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle -\frac{\partial G}{\partial
y}\end{array}\right|}{det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}=-\frac{\frac{\partial (F,G)}{\partial(u,y)}}{\frac{\partial(F,G)}{\partial(u,v)}}$.

Al determinante $det \left|\begin{array}{cc} \displaystyle
\frac{\partial F}{\partial u}&\displaystyle \frac{\partial
F}{\partial v}
\\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|$ lo llamamos Jacobiano y lo denotamos por $\displaystyle \frac{\partial (F,G)}{\partial (u,v)}$.

Ejemplo. Analizar la solubilidad del sistema
$$e^{u}+e^{v}=x+ye$$
$$ue^{u}+ve^{v}=xye$$
$\small{Solución}$ En este caso definimos
$$F(x,y,u,v)=e^{u}+e^{v}-x-ye=0$$
$$G(x,y,u,v)=ue^{u}+ve^{v}-xye=0$$
por lo que el sistema tendra solución si $\displaystyle{\det\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}\neq 0$

En este caso
$$\det\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|=\det\left|\begin{array}{cc} \displaystyle e^{u}&\displaystyle e^{v}\\ue^{u}+e^{e^{u}}&ve^{v}+e^{v}\end{array}\right|=e^{u}\left(ve^{v}+e^{v}\right)-e^{v}\left(ue^{u}+e^{u}\right)=ve^{u+v}-ue^{v+u}\neq 0$$
por lo tanto u y v se pueden ver en términos de x,y $\therefore$ se pueden calcular sus parciales en $u=0,~v=1,~x=1, ~y=1$ que es este caso dan
$$\displaystyle \frac{\partial u}{\partial x}=-\frac{\det
\left|\begin{matrix}-1&-ye\\e^{v}&ve^{v}+e^{v}\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-(ve^{v}+e^{v})+e^{v}ye}{ve^{u+v}-ue^{v+u}}\left.\right|{(0,1,1,1)}=\frac{2e-e^{2}}{e}=2-e$$ $$\displaystyle \frac{\partial v}{\partial x}=-\frac{\det \left|\begin{matrix}e^{u}&ue^{u}+e^{u}\\-1&-ye\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-ye^{u}e+ue^{u}+e^{u}}{ve^{u+v}-ue^{v+u}}\left.\right|{(0,1,1,1)}=\frac{e-1}{e}=1-e^{-1}$$
$$\displaystyle \frac{\partial u}{\partial y}=-\frac{\det
\left|\begin{matrix}-e&-xe\\e^{v}&ve^{v}+e^{v}\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-e(ve^{v}+e^{v})+e^{v}xe}{ve^{u+v}-ue^{v+u}}\left.\right|{(0,1,1,1)}=\frac{e^{2}+e^{2}-e^{2}}{e}=e$$ $$\displaystyle \frac{\partial v}{\partial y}=-\frac{\det \left|\begin{matrix}e^{u}&ue^{u}+e^{u}\\-e&-xe\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-e^{u}xe+e(ue^{u}+e^{u})}{ve^{u+v}-ue^{v+u}}\left.\right|{(0,1,1,1)}=\frac{e-e}{e}=0$$

Teorema de la Función Implícita (n-sistemas de ecuaciones

Considere las n-funciones
$$u_{i}=F_{i}(x_{1},…,x_{m},y_{1},…,y_{n}),~i=1,…,n$$ Sea $P=(\overline{x}{1},…,\overline{x}{m},\overline{y}{1},…,\overline{y}{n}) \in \mathbb{R}^{n+m}$ un punto tal que $F_{i}(P)=0$. Suponga que en una bola $\textit{B} \in \mathbb{R}^{n+m}$ de centro $P$ las funciones $F_{i}$ tienen (sus $m+n$) derivadas parciales continuas. Si el Jacobiano $$ \frac{\partial(F_{1},F_{2},…,F_{n})}{\partial (y_{1},y_{2},…,y_{n})}=\left|\begin{matrix}\frac{\partial F_{1}}{\partial y_{1}}&\frac{\partial F_{1}}{\partial y_{2}}&\cdots&\frac{\partial F_{1}}{\partial y_{n}}\\ \frac{\partial F_{2}}{\partial y_{1}}&\frac{\partial F_{2}}{\partial y_{2}}&\cdots&\frac{\partial F_{2}}{\partial y_{n}}\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial F_{n}}{\partial y_{1}}&\frac{\partial F_{n}}{\partial y_{2}}&\cdots&\frac{\partial F_{n}}{\partial y_{n}} \end{matrix}\right|\neq0~en~~P$$

entonces las expresiones
$F_{i}(x_{1},…,x_{m},y_{1},…,y_{n})=0$ y $G(x,y,u,v)=0$ definen funciones (implícitas)
$y_{i}=\varphi_{i}(x_{1},…,x_{m}),~i=1,…,n$ definidas en una vecindad $v$ de $(\overline{x}{1},…,\overline{x}{m})$ las cuales tienen derivadas parciales
continuas en $v$ que se pueden calcular como
$$\frac{\partial y_{i}}{\partial x_{j}}=\frac{\frac{\partial(F_{1},F_{2},…,F_{n})}{\partial (y_{1},…,y_{i-1},x_{j},y_{i+1},…,y_{n})}}{\frac{\partial (F_{1},F_{2},…,F_{n})}{\partial (y_{1},y_{2},…,y_{n})}}$$

Ejemplo. Considere las ecuaciones
$$\begin{matrix}
F(x,y,u,v,w)=x+y+u+v+w=0 \\
G(x,y,u,v,w)=x^{2}-y^{2}+u^{2}-2v^{2}+w^{2}+1=0 \\
H(x,y,u,v,w)=x^{3}+y^{3}+u^{4}-3v^{4}+8w^{4}+2=0
\end{matrix}$$

En el punto $P=(1,-1,1,-1,0)$, se tiene $F(P)=G(P)=H(P)=0$. Todas las derivadas parciales de F, G, H son continuas. Se tiene además que
$$\frac{\partial (F,G,H)}{\partial (u,v,w)}=\det\left|\begin{matrix}1&1&1\\ 2u&-4v&2w\\ 4u^{3}&-12v^{3}&32w^{2}\end{matrix}\right|_{\begin{matrix}u=1\\ v=-1\\ w=0\end{matrix}}=8\neq 0$$
Entonces el teorema asegura que en torno a P podemos despejar $u,v,w$ en términos de $x,y$ y establecer funciones
$$u=u(x,y),~v=v(x,y),~w=w(x,y)$$
las cuales tienen derivadas parciales continuas en una vecindad de $(1,-1)$ que se pueden calcular

$$\frac{\partial u}{\partial x}=-\frac{\frac{\partial (F,G,H)}{\partial (x,v,w)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}},\frac{\partial u}{\partial y}=-\frac{\frac{\partial (F,G,H)}{\partial (y,v,w)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}}$$

$$\frac{\partial v}{\partial x}=-\frac{\frac{\partial (F,G,H)}{\partial (u,x,w)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}},\frac{\partial v}{\partial y}=-\frac{\frac{\partial (F,G,H)}{\partial (u,y,w)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}}$$

$$\frac{\partial w}{\partial x}=-\frac{\frac{\partial (F,G,H)}{\partial (u,v,x)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}},~~\frac{\partial w}{\partial y}=-\frac{\frac{\partial (F,G,H)}{\partial (u,v,y)}}{\frac{\partial (F,G,H)}{\partial (u,v,w)}}$$

Teorema de la Función Implícita ($f:\mathbb{R}\rightarrow\mathbb{R}$

Teorema. Considere la función $y=f(x)$. Sea $(x_{0},y_{0}) \in \mathbb{R}^{2}$ un punto tal que $F(x_{0},y_{0})=0$. Suponga que la función $F$ tiene derivadas parciales continuas en alguna bola con centro $(x_{0},y_{0})$ y que $\displaystyle \frac{\partial F}{\partial y}(x_{0},y_{0})\neq 0$. Entonces $F(x,y)=0$ se puede resolver para $y$ en términos de $x$ y definir así una función $y=f(x)$ con dominio en una vecindad de $(x_{0},y_{0})$, tal que $y_{0}=f(x_{0})$, lo cual tiene derivadas continuas en $\mathcal{V}$ que pueden calcularse como $y’=f'(x)= \displaystyle \frac{\displaystyle \frac{\partial F}{\partial x}(x,y)}{\displaystyle \frac{\partial F}{\partial y}(x,y)}$, $x \in \mathcal{V}$.

Ejercicio. Si $$y’=f'(x)=-\displaystyle \frac{\displaystyle \frac{\partial F}{\partial
x}(x,y)}{\displaystyle \frac{\partial F}{\partial y}(x,y)}$$ calcular $y^{»}$

Solución. En este caso
$$y^{»}=-\frac{\left(\frac{\partial F}{\partial y}\right)\left[\frac{\partial^{2} F}{\partial x^{2}}\frac{dx}{dx}+\frac{\partial^{2} F}{\partial y\partial x}\frac{dy}{dx}\right]-\left(\frac{\partial F}{\partial x}\right)\left[\frac{\partial^{2} F}{\partial x\partial y}\frac{dx}{dx}+\frac{\partial^{2} F}{\partial y^{2}}\frac{dy}{dx}\right]}{\left(\frac{\partial F}{\partial y}\right)^{2}}$$
$$=-\frac{\left(\frac{\partial F}{\partial y}\right)\left[\frac{\partial^{2} F}{\partial x^{2}}+\frac{\partial^{2} F}{\partial y\partial x}\left(-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}\right)\right]-\left(\frac{\partial F}{\partial x}\right)\left[\frac{\partial^{2} F}{\partial x\partial y}\frac{dx}{dx}+\frac{\partial^{2} F}{\partial y^{2}}\left(-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}\right)\right]}{\left(\frac{\partial F}{\partial y}\right)^{2}}$$
$$=-\frac{\left(\frac{\partial F}{\partial y}\right)^{2}\left(\frac{\partial^{2} F}{\partial x^{2}}\right)-\left(\frac{\partial^{2} F}{\partial y\partial x}\right)\left(\frac{\partial F}{\partial x}\right)\left(\frac{\partial F}{\partial y}\right)-\left(\frac{\partial F}{\partial x}\right)\left(\frac{\partial F}{\partial y}\right)\left(\frac{\partial^{2} F}{\partial x\partial y}\right)+\left(\frac{\partial F}{\partial x}\right)^{2}\left(\frac{\partial^{2} F}{\partial y^{2}}\right)}{\left(\frac{\partial F}{\partial y}\right)^{3}}$$
$$=-\frac{\left(\frac{\partial F}{\partial y}\right)^{2}\left(\frac{\partial^{2} F}{\partial x^{2}}\right)-2\left(\frac{\partial^{2} F}{\partial y\partial x}\right)\left(\frac{\partial F}{\partial x}\right)\left(\frac{\partial F}{\partial y}\right)+\left(\frac{\partial F}{\partial x}\right)^{2}\left(\frac{\partial^{2} F}{\partial y^{2}}\right)}{\left(\frac{\partial F}{\partial y}\right)^{3}}$$

Teorema de la Función Implícita ($f:\mathbb{R}^{2}\rightarrow\mathbb{R}$)

Teorema. Considere la función $F(x,y,z)$. Sea $(x_{0},y_{0},z_{0}) \in
\mathbb{R}^{3}$ un punto tal que $F(x_{0},y_{0},z_{0})=0$. Suponga que la
función F tiene derivadas parciales $\displaystyle{\frac{\partial F}{\partial x},~\frac{\partial F}{\partial y},~\frac{\partial F}{\partial z}}$ continuas en alguna bola con
centro $(x_{0},y_{0},z_{0})$ y que $\displaystyle \frac{\partial
F}{\partial z}(x_{0},y_{0},z_{0})\neq 0$.
Entonces $F(x,y,z)=0$ se puede resolver para $z$ en términos de $x,y$
y definir así una función $z=f(x,y)$ con dominio en una vecindad de
$(x_{0},y_{0},z_{0})$, tal que $z_{0}=f(x_{0},y_{0})$, lo cual tiene derivadas continuas
en $\mathcal{V}$ que pueden calcularse como $$\frac{d z}{dx}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
x}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}~~~\frac{d z}{dy}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}$$

Ejercicio. Si
$$\frac{d z}{dx}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
x}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}$$ calcular $$\frac{\partial^{2}F}{\partial x^{2}}$$

Solución. Tenemos que
$$\frac{\partial^{2}F}{\partial x^{2}}=\frac{\partial}{\partial x}\left(-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
x}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}\right)=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial x^{2}} \frac{dx}{d x}+ \frac{\partial^{2} F}{\partial y\partial x} \frac{dy}{dx}+ \frac{\partial^{2} F}{\partial z\partial x} \frac{dz}{dx}\right]-\left( \frac{\partial F}{\partial x}\right)\left[ \frac{\partial^{2} F}{\partial x \partial z}\frac{dx}{d x}+ \frac{\partial^{2} F}{\partial y\partial z} \frac{dy}{dx}+ \frac{\partial^{2} F}{\partial z^{2}} \frac{dz}{dx}\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial x^{2}}+ \frac{\partial^{2} F}{\partial z\partial x} \frac{dz}{dx}\right]-\left( \frac{\partial F}{\partial x}\right)\left[ \frac{\partial^{2} F}{\partial x \partial z}+\frac{\partial^{2} F}{\partial z^{2}} \frac{dz}{dx}\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial x^{2}}+ \frac{\partial^{2} F}{\partial z\partial x} \left(-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}}\right)\right]-\left( \frac{\partial F}{\partial x}\right)\left[ \frac{\partial^{2} F}{\partial x \partial z}+\frac{\partial^{2} F}{\partial z^{2}}\left(-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}}\right)\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)^{2} \frac{\partial^{2} F}{\partial x^{2}}-2 \frac{\partial^{2} F}{\partial z\partial x} \frac{\partial F}{\partial x}\frac{\partial F}{\partial z}+\left(\frac{\partial F}{\partial x}\right)^{2}{\frac{\partial^{2} F}{\partial z^{2}}}}{\left(\frac{\partial F}{\partial z}\right)^{3}}$$

Ejercicio. Si
$$\frac{d z}{dy}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}$$ calcular $$\frac{\partial^{2}F}{\partial y^{2}}$$

Solución. tenemos que
$$\frac{\partial^{2}F}{\partial y^{2}}=\frac{\partial}{\partial y}\left(-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}\right)=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial y\partial x} \frac{dx}{d y}+ \frac{\partial^{2} F}{\partial y^{2}} \frac{dy}{dy}+ \frac{\partial^{2} F}{\partial z\partial y} \frac{dz}{dy}\right]-\left( \frac{\partial F}{\partial y}\right)\left[ \frac{\partial^{2} F}{\partial x \partial z}\frac{dx}{d y}+ \frac{\partial^{2} F}{\partial y\partial z} \frac{dy}{dy}+ \frac{\partial^{2} F}{\partial z^{2}} \frac{dz}{dy}\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial y^{2}}+ \frac{\partial^{2} F}{\partial z\partial y} \frac{dz}{dy}\right]-\left( \frac{\partial F}{\partial y}\right)\left[ \frac{\partial^{2} F}{\partial y \partial z}+\frac{\partial^{2} F}{\partial z^{2}} \frac{dz}{dy}\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial y^{2}}+ \frac{\partial^{2} F}{\partial z\partial y} \left(-\frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial z}}\right)\right]-\left( \frac{\partial F}{\partial y}\right)\left[ \frac{\partial^{2} F}{\partial y \partial z}+\frac{\partial^{2} F}{\partial z^{2}}\left(-\frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial z}}\right)\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)^{2} \frac{\partial^{2} F}{\partial y^{2}}-2 \frac{\partial^{2} F}{\partial z\partial y} \frac{\partial F}{\partial y}\frac{\partial F}{\partial z}+\left(\frac{\partial F}{\partial y}\right)^{2}{\frac{\partial^{2} F}{\partial z^{2}}}}{\left(\frac{\partial F}{\partial z}\right)^{3}}$$

Ejercicio. Si
$$\frac{d z}{dy}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}}{\displaystyle \frac{\partial F}{\partial z}}$$ calcular $$\frac{\partial^{2}F}{\partial y\partial x}$$

Solución. tenemos que
$$\frac{\partial^{2}F}{\partial y\partial x}=\frac{\partial}{\partial y}\left(\frac{\partial F}{\partial x}\right)=\frac{\partial}{\partial y}\left(-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
x}}{\displaystyle \frac{\partial F}{\partial z}}\right)=$$
$$-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial y\partial x} + \frac{\partial^{2} F}{\partial z\partial x} \frac{\partial z}{\partial y}\right]-\left(\frac{\partial F}{\partial x}\right)\left[ \frac{\partial^{2} F}{\partial y\partial z} +\frac{\partial^{2} F}{\partial z^{2}}\frac{\partial z}{\partial y}\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$-\frac{\left( \frac{\partial F}{\partial z}\right)\left[ \frac{\partial^{2} F}{\partial y\partial x} + \frac{\partial^{2} F}{\partial z\partial x} \left(-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}}{\displaystyle \frac{\partial F}{\partial z}}\right)\right]-\left(\frac{\partial F}{\partial x}\right)\left[ \frac{\partial^{2} F}{\partial y\partial z} +\frac{\partial^{2} F}{\partial z^{2}}\left(-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial
y}}{\displaystyle \frac{\partial F}{\partial z}}\right)\right]}{\left(\frac{\partial F}{\partial z}\right)^{2}}$$
$$=-\frac{\left( \frac{\partial F}{\partial z}\right)^{2} \frac{\partial^{2} F}{\partial y\partial x}- \frac{\partial^{2} F}{\partial z\partial x} \frac{\partial F}{\partial y}\frac{\partial F}{\partial z}-\frac{\partial^{2} F}{\partial y\partial z} \frac{\partial F}{\partial x}\frac{\partial F}{\partial z}+\frac{\partial^{2} F}{\partial z^{2}}\frac{\partial F}{\partial x}\frac{\partial F}{\partial y}}{\left(\frac{\partial F}{\partial z}\right)^{3}}$$

Teorema de la Función Implicita (version sistemas de ecuaciones)

Consideremos ahora el sistema

$au+bv-k_{1}x=0$
$cu+dv-k_{2}y=0$

con $a,b,c,d,k_{1},k_{2}$ constantes. Nos preguntamos cuando
podemos resolver el sistema para $u$ y $v$ en términos de $x$ y $y$.
Si escribimos el sistema como

$au+bv=k_{1}x$
$cu+dv=k_{2}y$

y sabemos que este sistema tiene solución si $det
\left|\begin{array}{cc} a&b\\
c&d\end{array}\right|\neq0$ en tal caso escribimos

$u=\displaystyle \frac{1}{det \left|\begin{array}{cc} a&b
\\c&d\end{array}\right|}(k_{1}dx-k_{2}by)$,~~$v=\displaystyle \frac{1}{det \left|\begin{array}{cc} a&b
\\c&d\end{array}\right|}(k_{2}ay-k_{1}cx)$.

Esta solución no cambiaría si consideramos

$au+bv=f_{1}(x,y)$
$cu+dy=f_{2}(x,y)$

donde $f_{1}$ y $f_{2}$ son funciones dadas de $x$ y $y$. La posibilidad de despejar las variables $u$ y $v$ en términos de $x$ y $y$ recae sobre los coeficientes de estas variables en las ecuaciones dadas.

Ahora si consideramos ecuaciones no lineales en $u$ y $v$ escribimos el sistema como

$g_{1}(u,v)=f_{1}(x,y)$
$g_{2}(u,v)=f_{2}(x,y)$

nos preguntamos cuando del sistema podemos despejar a $u$y $v$ en términos de $x$ y $y$. Mas generalmente, consideramos el problema siguiente, dadas las funciones $F$ y $G$ de las variables $u,v,x,y$ nos preguntamos cuando de las expresiones

$F(x,y,u,v)=0$
$G(x,y,u,v)=0$

podemos despejar a $u$ y $v$ en términos de $x$ y $y$ en caso de ser posible diremos que las funciones $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ son funciones implícitas dadas. Se espera que $\exists’$n funciones $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ en

$F(x,y,\varphi_{1}(x,y),\varphi_{2}(x,y)$
$G(x,y,\varphi_{1}(x,y),\varphi_{2}(x,y)$

con $(x,y)$ en alguna vecindad $V$. Suponiendo que existen $\varphi_{1}$ y $\varphi_{2}$ veamos sus derivadas

$\displaystyle \frac{\partial F}{\partial x}\displaystyle \frac{\partial x}{\partial x}+\displaystyle \frac{\partial F}{\partial y}\displaystyle
\frac{\partial y}{\partial x}+\displaystyle \frac{\partial
F}{\partial u}\displaystyle \frac{\partial u}{\partial
x}+\displaystyle \frac{\partial F}{\partial v}\displaystyle
\frac{\partial v}{\partial x}=0$ $~~ $ $\Rightarrow$ $~~$ $\displaystyle \frac{\partial F}{\partial u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial F}{\partial v}\displaystyle \frac{\partial v}{\partial x}=-\displaystyle \frac{\partial F}{\partial x}$

$\displaystyle \frac{\partial G}{\partial x}\displaystyle
\frac{\partial x}{\partial x}+\displaystyle \frac{\partial
G}{\partial y}\displaystyle \frac{\partial y}{\partial
x}+\displaystyle \frac{\partial G}{\partial u}\displaystyle
\frac{\partial u}{\partial x}+\displaystyle \frac{\partial
G}{\partial v}\displaystyle \frac{\partial v}{\partial x}=0$ $~~$ $\Rightarrow$ $~~$ $\displaystyle \frac{\partial G}{\partial
u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle
\frac{\partial G}{\partial v}\displaystyle \frac{\partial
v}{\partial x}=-\displaystyle \frac{\partial G}{\partial x}$

Lo anterior se puede ver como un sistema de 2 ecuaciones con 2 incógnitas $\displaystyle \frac{\partial u}{\partial x}$ y $\displaystyle \frac{\partial v}{\partial x}$. Aquí se ve que para que el sistema tenga solución

$det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|\neq0$ en $(P)$ (el $det$ Jacobiano) y según la regla de Cramer.

$\displaystyle \frac{\partial u}{\partial x}=-\frac{\det
\left|\begin{array}{cc} \displaystyle -\frac{\partial F}{\partial
x}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle -\frac{\partial G}{\partial x}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}{\det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}$, $~~$ $\displaystyle \frac{\partial v}{\partial x}=-\frac{\det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle -\frac{\partial F}{\partial x} \\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle -\frac{\partial G}{\partial x}\end{array}\right|}{det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial F}{\partial v} \\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial v}\end{array}\right|}$ $~~~~$ (con los dos $det$ Jacobianos).

Análogamente si derivamos con respecto a $y$ obtenemos

$\displaystyle \frac{\partial F}{\partial
u}\displaystyle \frac{\partial u}{\partial y}+\displaystyle
\frac{\partial F}{\partial v}\displaystyle \frac{\partial
v}{\partial y}=-\displaystyle \frac{\partial F}{\partial y}$

$\displaystyle \frac{\partial G}{\partial
u}\displaystyle \frac{\partial u}{\partial y}+\displaystyle
\frac{\partial G}{\partial v}\displaystyle \frac{\partial
v}{\partial y}=-\displaystyle \frac{\partial G}{\partial y}$

de donde
$\displaystyle \frac{\partial u}{\partial y}=-\frac{\det
\left|\begin{array}{cc} \displaystyle -\frac{\partial F}{\partial
y}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle -\frac{\partial G}{\partial y}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}{det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}$, $~~$ $\displaystyle \frac{\partial v}{\partial y}=-\frac{\det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle -\frac{\partial F}{\partial y} \\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle -\frac{\partial G}{\partial y}\end{array}\right|}{det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial F}{\partial v} \\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial v}\end{array}\right|}$ $~~~~$ (con los dos $det$ Jacobianos).

Al determinante $det \left|\begin{array}{cc} \displaystyle
\frac{\partial F}{\partial u}&\displaystyle \frac{\partial
F}{\partial v}
\\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|$ lo llamamos Jacobiano y lo denotamos por $\displaystyle \frac{\partial (F,G)}{\partial (u,v)}$.

Teorema de la Función Implícita (sistemas de ecuaciones)

Teorema 3. Considere las funciones $z_{1}=F(x,y,u,v)$ y $z_{2}=G(x,y,u,v)$. Sea $P=(x,y,u,v) \in \mathbb{R}^{4}$ un punto tal que $F(P)=G(P)=0$. Suponga que en una bola $\textit{B} \in \mathbb{R}^{4}$ de centro $P$ las funciones $F$ y $G$ tienen (sus cuatro) derivadas parciales continuas. Si el Jacobiano $\displaystyle \frac{\partial
(F,G)}{\partial (u,v)}(P)\neq0$ entonces las expresiones $F(x,y,u,v)=0$ y $G(x,y,u,v)=0$ definen funciones (implícitas) $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ definidas en una vecindad $v$ de $(x,y)$ las cuales tienen derivadas parciales continuas en $v$ que se pueden calcular como se menciona arriba.

Demostración. Dado que $$det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|\neq 0$$ entonces $\displaystyle{\frac{\partial F}{\partial u}(p)}$, $\displaystyle{\frac{\partial F}{\partial v}(p)}$, $\displaystyle{\frac{\partial G}{\partial u}(p)}$, $\displaystyle{\frac{\partial G}{\partial v}(p)}$ no son cero al mismo tiempo, podemos suponer sin perdida de generalidad que $\displaystyle{\frac{\partial G}{\partial v}(p)}\neq0$. Entonces la función $z_{1}=G(x,y,u,v)$ satisface las hipótesis del T.F.I y en una bola abierta con centro p, v se puede escribir como $v=\psi(x,y,u)$.

Hacemos ahora
$$H(x,y,u)=F(x,y,u,\psi(x,y,u))$$ y tenemos que
$$\frac{\partial H}{\partial u}=\frac{\partial F}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial u}+\frac{\partial F}{\partial u}\frac{\partial u}{\partial u}+\frac{\partial F}{\partial v}\frac{\partial \psi}{\partial u}=\frac{\partial F}{\partial u}+\frac{\partial F}{\partial v}\frac{\partial \psi}{\partial u}$$

por otro lado
$$\frac{\partial \psi}{\partial u}=-\frac{\frac{\partial G}{\partial u}}{\frac{\partial G}{\partial v}}$$
por lo tanto
$$\frac{\partial H}{\partial u}=\frac{\partial F}{\partial u}+\frac{\partial F}{\partial v}\frac{\partial \psi}{\partial u}=\frac{\partial F}{\partial u}+\frac{\partial F}{\partial v}\left(-\frac{\frac{\partial G}{\partial u}}{\frac{\partial G}{\partial v}}\right)=\frac{\frac{\partial F}{\partial u}\frac{\partial G}{\partial v}-\frac{\partial F}{\partial v}\frac{\partial G}{\partial u}}{\frac{\partial G}{\partial v}}\neq0$$por lo tanto para $H(x,y,u)=0$ tenemos que existe una función $u=\varphi_{1}(x,y)$ y por lo tanto $v=\psi(x,y,u)=\psi(x,y,\varphi_{1}(x,y,u))=\varphi_{2}(x,y)$ y por tanto $u,v $ se pueden expresar en términos de $x,y$ en una vecindad de $p$. $\square$

Introduccion

El Teorema de la función implicita versión para funciones $f:\mathbb{R}\rightarrow\mathbb{R}$

Teorema 1. Considere la función $y=f(x)$. Sea $(x_{0},y_{0}) \in
\mathbb{R}^{2}$ un punto tal que $F(x_{0},y_{0})=0$. Suponga que la función $F$ tiene derivadas parciales continuas en alguna bola con centro $(x_{0},y_{0})$ y que $\displaystyle \frac{\partial F}{\partial y}(x_{0},y_{0})\neq 0$. Entonces $F(x,y)=0$ se puede resolver para $y$ en términos de $x$ y definir así una función $y=f(x)$ con dominio en una vecindad de $(x_{0},y_{0})$, tal que $y_{0}=f(x_{0})$, lo cual tiene derivadas continuas en $\mathcal{V}$ que pueden calcularse como $y’=f'(x)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial x}(x,y)}{\displaystyle \frac{\partial F}{\partial y}(x,y)}$, $x \in \mathcal{V}$.

Demostración. Como $\displaystyle{\frac{\partial
F}{\partial y}(x_{0},y_{0})\neq 0}$ supongamos sin perdida de generalidad que $\displaystyle{\frac{\partial F}{\partial y}(x_{0},y_{0})> 0}$. Por ser $\displaystyle{\frac{\partial F}{\partial y}}$ continua en una vecindad de $(x_{0},y_{0})$ entonces exite un cuadrado S, centrado en $(x_{0},y_{0})$ totalmente contenido en esa vecindad, en donde $\displaystyle{\frac{\partial F}{\partial y}(x,y)> 0}$ $\forall~x,y\in S$.Sea
$$S=\left\{(x,y)\in\mathbb{R}^{2}~|~|x-x_{0}|<h~y~|y-y_{0}|<k \right\}$$

En todo punto $(x,y)$ que pertenece a $S$, $\displaystyle{\frac{\partial F}{\partial y}(x,y)>0}$. Esto quiere decir que en $S$, $F$ es creciente y fijando $x_{0}$ en $[x_{0}-h,x_{0}+h]$ se tiene que $F$ es creciente en $[y_{0}-k,y_{0}+k]$ y se anula en $y_{0}$, por lo que
$$F(x_{0},y_{0}-k)<0~~yF(x_{0},y_{0}+k)>0$$ Consideremos ahora el par de funciones $F(x,y_{0}-k)$ y $F(x,y_{0}+k)$ definidas en el intervalo $(x_{0}-k,x_{0}+k)$. Donde ambas funciones solo tienen x como variable. La primera función cumple $F(x_{0},y_{0}-k)<0$ y por ser continua en $x_{0}$, es negativa en toda una vecindad $(x_{0}-h_{1}x_{0}+h_{1})$ de $x_{0}$. Análogamente, la segunda función cumple $F(x_{0},y_{0}+k)>0$ y por ser continua en $x_{0}$, es positiva en toda una vecindad $(x_{0}-h_{2}x_{0}+h_{2})$ de $x_{0}$. Sea $h=\min{h_{1},h_{2}}$. Entonces para toda $x$ tal que $|x-x_{0}|~y~F(x,y_{0}+k)>0$ Fijemos $x$ en el intervalo $(x_{0}-h,x_{0}+h)$, y consideremos a $F(x,y)$, sólo como función de $y$, sobre $[y_{0}-k,y_{0}+k]$. Esta función cumple que

$$F(x,y_{0}-k)<0~y~F(x,y_{0}+k)>0$$

por lo tanto según el teorema del valor intermedio, existe un único y en $(y_{0}-k,y_{0}+k)$ tal que $F(x,y)=0$. Así queda establecida la existencia y unicidad de la función $y=f(x)$. Donde además, $y_{0}=f(x_{0})$, y para todo $x\in(x_{0}-h,x_{0}+h)$ $$F(x,f(x))=0,y~~\frac{\partial F}{\partial y}(x_{0},y_{0})\neq 0$$

Vamos a comprobar que la función es continua, para ello se tiene
$$x\in[x_{0}-h,x_{0}+h]~\Rightarrow~|x-x_{0}|<h$$
tomando $h<\delta$ se tiene
$$|x-x_{0}|<\delta$$
esto quiere decir que
$$|y-y_{0}|<k$$ es decir$$|f(x)-f(x_{0})|,\frac{\partial F}{\partial y}(x_{0},y_{0})$$
existen y son continuas entonces $F$ es diferenciable por lo que
$$F(x_{0}+h,y_{0}+k)-F(x_{0},y_{0})=\frac{\partial F}{\partial x}(x_{0},y_{0})h+\frac{\partial F}{\partial y}(x_{0},y_{0})k+R(h,k)$$
Tenemos que $F$ es continua por lo que
$$F(x_{0}+h,y_{0}+k)-F(x_{0},y_{0})=0sih,k\rightarrow 0$$
también
$$R(h,k)\rightarrow 0sih,k\rightarrow 0$$
por lo que
$$\frac{\partial F}{\partial x}(x_{0},y_{0})h+\frac{\partial F}{\partial y}(x_{0},y_{0})k=0$$
esto es
$$\frac{k}{h}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0})}{\frac{\partial F}{\partial y}(x_{0},y_{0})}$$
y cuando $h,k\rightarrow 0$ se tiene
$$\frac{dy}{dx}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0})}{\frac{\partial F}{\partial y}(x_{0},y_{0})}$$

Importante: Este es un resultado que garantiza la
existencia de una función $y=f(x)$ definida implícitamente por
$F(x,y)=0$. Esto es, puede resolverse para $y$ en términos de $x$,
pero no nos dice como hacer el despeje.

Ejemplo. Considere la función $F(x,y)=e^{2y+x}+\sin(x^{2}+y)-1$ en el punto (0,0) tenemos $F(0,0)=0$. Las derivadas parciales de $F$ son
$F_{x}=e^{2y+x}+2x\cos(x^{2}+y)$
$F_{y}=2e^{2y+x}+\cos(x^{2}+y)$

que son siempre continuas. Además, $\displaystyle \frac{\partial F}{\partial y}(0,0)=3\neq0$ de modo que $\textbf{T.F.Im.}$ garantiza una vecindad de $x=0$ en la cual podemos definir una función $y=f(x)$ tal que $F(x,f(x))=0$. Obsérvese que en este caso no podemos hacer explícita la función $y=f(x)$ sin embargo tal función existe y su derivada es

$y’=f'(x)=\displaystyle -\frac{\displaystyle \frac{\partial F}{\partial x}}{\displaystyle \frac{\partial F}{\partial y}}=\displaystyle \frac{e^{2y+x}+2x\cos(x^{2}+y)}{2e^{2y+x}+\cos(x^{2}+y)}$

Ejemplo. Considere $F(x,y)=x^{4}-e^{xy^{3}-1}$ en el punto (1,1) $F(1,1)=1-1=0$, $F_{x}=4x^{3}-y^{3}e^{xy^{3}-1}$ Por lo tanto, $F_{x}|{(1,1)}=3$, $F{y}=-3xye^{xy^{3}-1}$
Y así, $F_{y}|_{(1,1)}=-3$, y $\displaystyle \frac{\partial F}{\partial y}=-3\neq0$.

El $\textbf{T.F.Im.}$ nos garantiza que en los alrededores de (1,1) el nivel cero de $F$ se ve como la gráfica de la función $y=f(x)$ y que su derivada es $y’=\displaystyle
\frac{-4x^{3}-y^{3}e^{xy^{3}-1}}{-3xy^{2}e^{xy^{3}-1}}$.

Observe que en este caso la función $F$ permite hacer el despeje en términos de $x$.

$F(x,y)=x^{4}-e^{xy^{3}-1}=0$
$x^{4}=e^{xy^{3}-1}$
$\ln (x^{4})=xy^{3}-1$
$\left(\displaystyle \frac{\ln (x^{4})+1}{x}\right)^{\frac{1}{3}}=y=f(x)$ que al derivar se debe de llegar al mismo resultado.

Ejemplo. Considere $F(x,y)=x^{2}-y^{3}-1$ en el punto $(x_{0},y_{0})$ con $y_{0}\neq 0$ tal que $F(x_{0},y_{0})=0$, $F_{x}=2x,~~F_{y}=2y$
Por lo tanto, $F_{x}|{(x{0},y_{0})}=2x_{0}$,
Y así, $F_{y}|{(x{0},y_{0})}=2y_{0}$, y $\displaystyle \frac{\partial F}{\partial y}=2y_{0}\neq0$.
El $\textbf{T.F.Im.}$ nos garantiza que en los alrededores de $(x_{0},y_{0})$ el
nivel cero de $F$ se ve como la gráfica de la función $y=f(x)$ y que su derivada es
$$y'(x)=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0})}{\frac{\partial F}{\partial y}(x_{0},y_{0})}$$
en este caso
$$y'(x)=-\frac{2x_{0}}{2y_{0}}=-\frac{x_{0}}{y_{0}}$$
si $y_{0}>0$ tal función es $f(x)=\sqrt{1-x^{2}}$ por lo que
$$y’=-\frac{x}{\sqrt{1-x^{2}}}=-\frac{x}{y}$$
si $y_{0}<0$ tal función es $f(x)=-\sqrt{1-x^{2}}$ por lo que
$$y’=-\frac{-x}{-\sqrt{1-x^{2}}}=-\frac{x}{y}$$

El Teorema de la función implicita versión para funciones $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$

Considere la función $F(x,y,z)$. Sea $(x_{0},y_{0},z_{0}) \in \mathbb{R}^{3}$ un punto tal que $F(x_{0},y_{0},z_{0})=0$. Suponga que la función $F$ tiene derivadas parciales $\displaystyle{\frac{\partial F}{\partial x},~\frac{\partial F}{\partial y},~\frac{\partial F}{\partial z}}$ continuas en alguna bola con centro $(x_{0},y_{0},z_{0})$ y que $\displaystyle \frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\neq 0$.
Entonces $F(x,y,z)=0$ se puede resolver para $z$ en términos de $x,y$ y definir así una función $z=f(x,y)$ con dominio en una vecindad de
$(x_{0},y_{0},z_{0})$, tal que $z_{0}=f(x_{0},y_{0})$, lo cual tiene derivadas continuas
en $\mathcal{V}$ que pueden calcularse como $$\frac{d z}{dx}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial x}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}~~~\frac{d z}{dy}(x,y)=-\displaystyle \frac{\displaystyle \frac{\partial F}{\partial
y}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}$$
$\textbf{Importante:}$ Este es un resultado que garantiza la existencia de una función $z=f(x,y)$ definida implícitamente por $F(x,y,z)=0$. Esto es, puede resolverse para $z$ en términos de $x,y$, pero no nos dice como hacer el despeje.

Demostración. Consideremos el par de funciones
$$F(x,y,z_{0}-\ell)yF(x,y,z_{0}+\ell)$$
definidas para $(x,y)\in[x_{0}-h,x_{0}+h]\times [y_{0}-k,y_{0}+k]$\La primera satisface
$$F(x_{0},y_{0},z_{0}-\ell)<0$$ la segunda cumple $$F(x_{0},y_{0},z_{0}+\ell)>0$$
Fijemos $(x,y)$ en $[x_{0}-h,x_{0}+h]\times [y_{0}-k,y_{0}+k]$ y consideramos $F(x,y,z)$ solo como función de z, sobre $[z_{0}-\ell,z_{0}+\ell]$. Esta función cumple
$$F(x,y,z_{0}-\ell)<0~y~F(x,y,z_{0}+\ell)>0$$
por lo que al aplicar el Teorema del valor intermedio, obteniendose un único z en $(z_{0}-\ell,z_{0}+\ell)$ en donde $F(x,y,z)=0$.Queda así establecida la existencia y unicidad de la función $z=f(x,y)$ con dominio $[x_{0}-h,x_{0}+h]\times [y_{0}-k,y_{0}+k]$ y rango $[z_{0}-\ell,z_{0}+\ell]$ Vamos a probar que dicha f es continua, para ello si
$$\left(\begin{matrix}x\in [x_{0}-h,y_{0}+h] , y\in [y_{0}-k,y_{0}+k] \end{matrix}\right)~\Rightarrow~\left(\begin{matrix}|x-x_{0}|<h\|y-y_{0}|<k\end{matrix}\right)$$
por lo que
$$|(x,y)-(x_{0},y_{0})|<|x-x_{0}|+|y-y_{0}|<h+k$$
si $h<k$
$$|(x,y)-(x_{0},y_{0})|<2k=\delta$$
donde
$$|f(x,y)-f(x_{0},y_{0})|=|z-z_{0}|<\ell=\epsilon$$
por lo tanto $f(x,y)$ es continua.Ahora si suponemos que $\displaystyle{\frac{\partial F}{\partial x},~\frac{\partial F}{\partial y}},~\frac{\partial F}{\partial z}$ son continuas en los alrededores de $(x_{0},y_{0},z_{0})$ en tonces F es diferenciable y se tiene
$$F(x_{0}+h,y_{0},z_{0}+\ell)-F(x_{0},y_{0},z_{0})=\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})h+\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})0+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell+R(h,k,\ell)$$

De donde
$$F(x_{0}+h,y_{0},z_{0}+\ell)-F(x_{0},y_{0},z_{0})\rightarrow 0$$
$$R(h,k,\ell)\rightarrow 0$$
por lo que
$$\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})h+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell=0$$
$$~\Rightarrow~\frac{h}{\ell}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$
y cuando $h,\ell\rightarrow 0$ se tiene
$$\frac{dz}{dx}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$
Análogamente
$$F(x_{0},y_{0}+k,z_{0}+\ell)-F(x_{0},y_{0},z_{0})=\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})0+\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})k+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell+R(h,k,\ell)$$
De donde
$$F(x_{0},y_{0}+k,z_{0}+\ell)-F(x_{0},y_{0},z_{0})\rightarrow 0$$
$$R(h,k,\ell)\rightarrow 0$$
por lo que
$$\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})k+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell=0$$
$$~\Rightarrow~\frac{k}{\ell}=-\frac{\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$
y cuando $h,\ell\rightarrow 0$ se tiene
$$\frac{dz}{dy}=-\frac{\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$ $\square$

Introducción

En esta entrada conoceremos más propiedades de los espacios métricos compactos. Veremos qué ocurre cuando les es aplicada una función continua. Esto nos relacionará dos espacios métricos entre sí a través de los subconjuntos. Podremos concluir información acerca de la imagen de una función cuando ciertas condiciones se cumplen. Comencemos con la siguiente:

Proposición: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. Si $\phi:X \to Y$ es una función continua y $A \subset X$ es compacto, entonces la imagen de $A$ bajo $\phi$, es decir, $\phi(A),$ es un conjunto compacto en $(Y,d_Y).$

Demostración:
Sea $\mathcal{C}= \{A_i: i \in \mathcal{I}\}$ una cubierta abierta de $\phi (A)$. Como $\phi$ es continua entonces la imagen inversa de $A_i,$ es decir, el conjunto $\phi ^{-1}(A_i), i \in \mathcal{I}$ es un conjunto abierto en $X$. No es difícil probar que $\{\phi ^{-1}(A_i):i \in \mathcal{I}\}$ es una cubierta abierta de $A.$ (Ejercicio).

Como $A$ es compacto, entonces existe una subcubierta finita $\{\phi ^{-1}(A_{i_1}),\phi ^{-1}(A_{i_2}),…,\phi ^{-1}(A_{i_m}) \}$ con $m \in \mathbb{N}$ tal que $A \subset \underset{1\leq j \leq m}{\bigcup}\phi ^{-1}(A_{i_j}).$ Esto significa que $\{A_{i_1},A_{i_2},…,A_{i_m}\}$ es una subcubierta en $Y$ de $\mathcal{C}$ para $\phi (A)$. (¿Por qué?) Por lo tanto $\phi (A)$ es compacto.

Ejemplos

La función valor absoluto en un intervalo cerrado

La función $sen(4x)$

La función $e^x$

Es resultado conocido que si $\phi: [0,1] \to \mathbb{R}$ es una función continua, entonces $\phi([0,1])= [a,b]$ donde $a = min \{f(x)|0 \leq x \leq 1 \} \, $ y $ \, b = max \{f(x)|0 \leq x \leq 1 \}.$ (Ver Teorema del máximo-mínimo). En efecto $[a,b]$ es un intervalo cerrado en $\mathbb{R}$ y por tanto es compacto.

Bajo la misma idea podemos considerar a la función $\psi: \mathbb{R} \to \mathbb{R}^2$ dada por $\psi(t)=(t,\phi(t))$. Entonces, la curva de esta función es un conjunto compacto en $\mathbb{R}^2$

En la entrada anterior vimos que un conjunto compacto es cerrado y acotado. Podemos concluir el siguiente:

Corolario: Sea $A$ compacto. Entonces una función continua $\phi:A \subset X \to Y$ es acotada, pues la imagen bajo $\phi$ en el compacto es compacta y, por lo tanto, acotada. También podemos concluir que $\phi(A)$ es cerrada.

Este resultado nos permite delimitar una función en el espacio euclidiano de $\mathbb{R}$ con dos puntos importantes en el contradominio de la función: el máximo y el mínimo.

Probablemente este resultado te sea familiar de los cursos de cálculo:

Proposición: Sea $f:A\subset \mathbb{R}^n \to \mathbb{R}$ una función continua con $A$ cerrado y acotado (y por tanto compacto en $\mathbb{R}^n$). Entonces $f \,$ alcanza su mínimo y máximo en $A.$

En otros espacios métricos puede generalizarse como sigue:

Proposición: Sea $f:A \to \mathbb{R}$ una función continua con $A$ espacio métrico compacto y $\mathbb{R}$ con la métrica usual. Entonces $f$ alcanza su mínimo y máximo en $A$, es decir, existen puntos $x_1$ y $x_2$ en $A$ tales que para toda $x \in A$ se cumple que:
$$f(x_1) \leq x \leq f(x_2)$$

Demostración:
Si $A$ es compacto, la proposición anterior nos muestra que $f(A)$ es cerrado y acotado. Sea $m_0= inf\{f(x):x \in A\}$. Entonces $m_0 \in \overline{f(A)}$ y como $f(A)$ es cerrado, se concluye que $m_0 \in f(A)$, de modo que existe $x_1 \in A$ tal que $f(x_1)=m_0 \, $ por lo tanto $f$ alcanza su mínimo en $A$.

La demostración de que $f$ alcanza su máximo es análoga y se deja como ejercicio.

Proposición: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos con $X$ compacto y $\phi:X \to Y$ inyectiva y continua. Entonces existe la función inversa $\phi^{-1}$ en $\phi(X)$ y es continua en $\phi(X)$.

Demostración:
Para demostrar que $\phi^{-1}:\phi(X) \to X$ es una función continua, basta probar que la imagen inversa de esta función aplicada en conjuntos cerrados en $X$, es un conjunto cerrado en $Y$. Si $A$ es cerrado en $X$ entonces la imagen inversa respecto a la función $\phi^{-1}$ está dada por $\phi(A)$. Como $A$ es cerrado en un compacto entonces es compacto, de modo que $\phi(A)$ también es compacto y, por lo tanto, es cerrado en $Y$. Esto prueba que $\phi^{-1}$ es continua.

Finalizaremos esta entrada presentando un resultado que se deduce del anterior. La solución se propone como ejercicio al lector:

Proposición: Si $\phi:X \to Y$ es una función biyectiva y continua entre espacios métricos compactos, entonces es un homeomorfismo.

Más adelante…

Continuaremos visualizando aplicaciones de funciones continuas sobre conjuntos compactos, pero esta vez bajo una nueva definición: la continuidad uniforme.

Tarea moral

1. Como parte de la prueba de la primera proposición, muestra que en efecto $\{\phi ^{-1}(A_i):i \in \mathcal{I}\}$ es una cubierta abierta de $A$.
2. Argumenta la parte de la demostración de la primera proposición, en la que se afirma que si $A \subset \underset{1\leq j \leq m}{\bigcup}\phi ^{-1}(A_{i_j}),$ entonces $\{A_{i_1},A_{i_2},…,A_{i_m}\}$ es una subcubierta en $Y$ de $\mathcal{C}$ para $\phi (A)$.
3. Prueba que si $f:A \to \mathbb{R}$ es una función continua con $A \subset \mathbb{R}^n$ cerrado y acotado, entonces $f$ alcanza su máximo en $A.$
4. Prueba que si $X$ y $Y$ son homeomorfos, entonces $X$ es compacto si y solo si $Y$ es compacto.
5. Demuestra que si $\phi:X \to Y$ es una función biyectiva y continua entre espacios métricos compactos, entonces es un homeomorfismo.

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introduccion

El método de los mínimos cuadrados

El método de mínimos cuadrados se aplica para ajustar rectas a una serie de datos presentados como punto en el plano.
Suponagamos que se tienen los siguientes datos para las variables $x$,$y$.

Esta situación se puede presentar en estudios experimentales, donde se estudia la variación de cierta magnitud x en función de otra magnitud y. Teóricamente es de esperarse que la relación entre estas variables sea lineal, del tipo
$$y=mx+b$$
El método de mínimos cuadrados nos proporciona un criterio con el cual podremos obtener la mejor recta que representa a los puntos dados. Se desearía tener
$$y_{i}=mx_{i}+b$$
para todos los puntos $(x_{i},y_{i})$ de $i=1,…,n$. Sin embargo, como en general
$$y_{i}\neq mx_{i}+b$$
se pide que la suma de los cuadrados de las diferencias (las desviaciones)
$$y_{i}-(mx_{i}+b)$$
sea la menor posible.

Se requiere
$$S=(y_{1}-(mx_{1}+b))^{2}+(y_{2}-(mx_{2}+b))^{2}+\cdots+(y_{n}-(mx_{n}+b))^{2}$$
$$=\sum_{i=1}^{n}(y_{i}-(mx_{i}+b))^{2}$$
sea lo más pequeña posible. Los valores de m y b que cumplan con esta propiedad, determinan la recta
$$y=mx+b$$
que mejor representa el comportamiento lineal de los puntos $(x_{i},y_{i})$

Consideremos entonces la función f de las variables m y b dada por
$$f(m,b)=\sum_{i=1}^{n}(y_{i}-(mx_{i}+b))^{2}$$
donde los puntos críticos de esta función se obtienen al resolver el sistema
$$\frac{\partial f}{\partial m}=\sum_{i=1}^{n}2(y_{i}-(mx_{i}+b))(-x_{i})=2\sum_{i=1}^{n}x_{i}(y_{i}-(mx_{i}+b))=0$$
$$\frac{\partial f}{\partial b}=\sum_{i=1}^{n}2(y_{i}-(mx_{i}+b))(-1)=-2\sum_{i=1}^{n}(y_{i}-(mx_{i}+b))=0$$
De la segunda ecuación obtenemos
$$\sum_{i=1}^{n}y_{i}-m\sum_{i=1}^{n}x_{i}-\sum_{i=1}^{n}b=0$$
de donde
$$b=\frac{1}{n}\sum_{i=1}^{n}y_{i}-m\left(\frac{1}{n}\sum_{i=1}^{n}x_{i}\right)$$
Llamemos
$$\overline{x}=\frac{1}{n}\sum_{i=1}^{n}x_{i}$$
$$\overline{y}=\frac{1}{n}\sum_{i=1}^{n}y_{i}$$
que son las medias aritméticas de los valores $x_{i},~y_{i}$ respectivamente. Entonces
$$b=\overline{y}-m\overline{x}$$

sustituyendo en la ecuación
$$\frac{\partial f}{\partial m}=0$$
nos queda
$$\sum_{i=1}^{n}x_{i}(y_{i}-mx_{i}-(\overline{y}-m\overline{x}))=0$$
de donde se obtiene
$$m=\frac{\sum_{i=1}^{n}x_{i}(y_{i}-\overline{y})}{\sum_{i=1}^{n}x_{i}(x_{i}-\overline{x})}$$
En resumen, la función
$$f(m,b)=\sum_{i=1}^{n}(y_{i}-(mx_{i}+b))^{2}$$
tiene un único punto crítico para
$$m=\frac{\sum_{i=1}^{n}x_{i}(y_{i}-\overline{y})}{\sum_{i=1}^{n}x_{i}(x_{i}-\overline{x})},~~~b=\overline{y}-m\overline{x}$$
Ahora vamos a verificar que en dicho punto crítico se alcanza un mínimo local, para lo cual recurrimos a nuestro criterio de la segunda derivada, en este caso
$$\frac{\partial^{2} f}{\partial m^{2}}=-2\sum_{i=1}^{n}-x_{i}^{2}=2\sum_{i=1}^{n}x_{i}^{2}$$
$$\frac{\partial^{2} f}{\partial m \partial b}=-\sum_{i=1}^{n}-x_{i}=2\sum_{i=1}^{n}x_{i}$$
$$\frac{\partial^{2} f}{\partial b^{2}}=-2\sum_{i=1}^{n}(-1)=2n$$

Tenemos que
$$\frac{\partial^{2} f}{\partial m^{2}}>0$$
Por otro lado
$$\left(2\sum_{i=1}^{n}x_{i}\right)^{2}-\left(2\sum_{i=1}^{n}x_{i}^{2}\right)(2n)<0$$
esta desigualdad es equivalente a
$$\left(\sum_{i=1}^{n}x_{i}\right)^{2}<n\sum_{i=1}^{n}x_{i}$$
La cual no es mas que la desigualdad de Cauchy-Schwarz aplicada a los vectores $(1,1,…,1)$ y $(x_{1},x_{2},…,x_{n})$ de $\mathbb{R}^{n}$. Por lo que la función f posee un mínimo local en el punto punto crítico dado.

Ejemplo. Se obtuvieron experimentalmente los siguientes valores de las variables x, y, los cuales se sabe que guardan entre sí una relación lineal

Vamos a encontrar la recta que mejor se ajusta a estos datos, según el método de mínimos cuadrados se tiene
$$\overline{x}=\frac{1+2+3+4}{2}=2.5$$
$$\overline{y}=\frac{1.4+1.1+0.7+0.1}{4}=0.825$$
Aplicando la fórmula obtenida para m y b obtenemos
$$m=\frac{\sum_{i=1}^{n}x_{i}(y_{i}-\overline{y})}{\sum_{i=1}^{n}x_{i}(x_{i}-\overline{x})}=\frac{1(1.4-0.825)+2(1.1-0.825)+3(0.7-0.825)+4(0.1-0.825)}{1(1-2.5)+2(2-2.5)+3(3-2.5)+4(4-2.5)}$$
$$=\frac{-2.15}{5}=-0.43$$
$$b=\overline{y}-m\overline{x}=0.825-(0.43)(2.5)=1.9$$

por lo que la recta que mejor ajusta los datos proporcionados

La suma de las diferencias de la recta y real con la y predicha por la ecuación obtenida es
$$-0.07+0.06+0.09-0.08=0$$
Es decir nuestra recta efectivamente compensa los puntos que quedaron por encima con puntos que quedaron por debajo. Gráficamente esto se ve.

La mejor recta que ajusta los datos del ejemplo.

Mas adelante

Tarea Moral

1.- Explica con tus propias palabras la idea de un punto o puntos críticos de una función entudiado con anterioridad y su relación subyacente con un conjunto de datos dados donde unos dependen de otros (por ejemplo: valores de temperatura y presión). Básicamentte es describir de qué manera interviene el método de mínimos cuadrados en un ajuste lineal, considera como concepto clave el mínimo de una función, en este caso cuando nos presentan varios valores donde dependen unos de otros entre sí, ¿cuál es la función que nos interesa? Nota: en el área de estadística esta herramienta recibe el nombre de regresión lineal simple.

2.- Una empresa de ecommerce desea predecir sus ventas mensuales para el próximo trismestre basándose en los datos de los últimos 6 meses. Se asume que existe una relación lineal entre el tiempo (mes) y las ventas como indica la siguiente tabla:

Determina la recta de la forma $$y=mx+b$$ que mejor se ajusta a los datos

3.- Pronostica la venta para el mes 7.

4.- Grafica los datos para corroborar geométricamente el ejercicio anterior.

5.- Aplica los ejercicios 2 al 4 en python o R de forma extendida, es decir, define y calcula las variables necesarias: $$\overline{x}, \overline{y}, b,m$$

Enlaces