Introducción
En caso contrario a las derivadas, algunas integrales no se pueden resolver o son muy difíciles de resolver y esto es porque ninguna técnica puede ni podrá que tales integrales se puedan expresar en términos de funciones elementales, por lo que a estas integrales se recurre a aproximarlas numéricamente, por lo que en esta entrada enseñaremos solo algunos métodos numéricos para integrales definidas, ya que hay un mundo de métodos numéricos.
Métodos numéricos de integración
La idea de evaluar una integral definida $\int_{a}^{b}f(x)dx$ consiste en determinar una fórmula $F(x)$ para una de las antiderivadas $f(x)$ y calcular el número $F(b)-F(a)$, sin embargo, en algunas ocasiones es difícil o incluso imposible hallar una antiderivada, por ejemplo, es difícil hallar de manera exacta la siguiente integral definida:
$$\int_{0}^{1} e^{x^{2}}dx$$
Por lo que en estos casos se necesita hallar valores aproximados a estas integrales definidas usando algunos métodos de aproximación como la regla del punto medio o la regla del trapecio.
Regla del punto medio
Para el método de la regla del punto medio comenzamos a deducir este método.
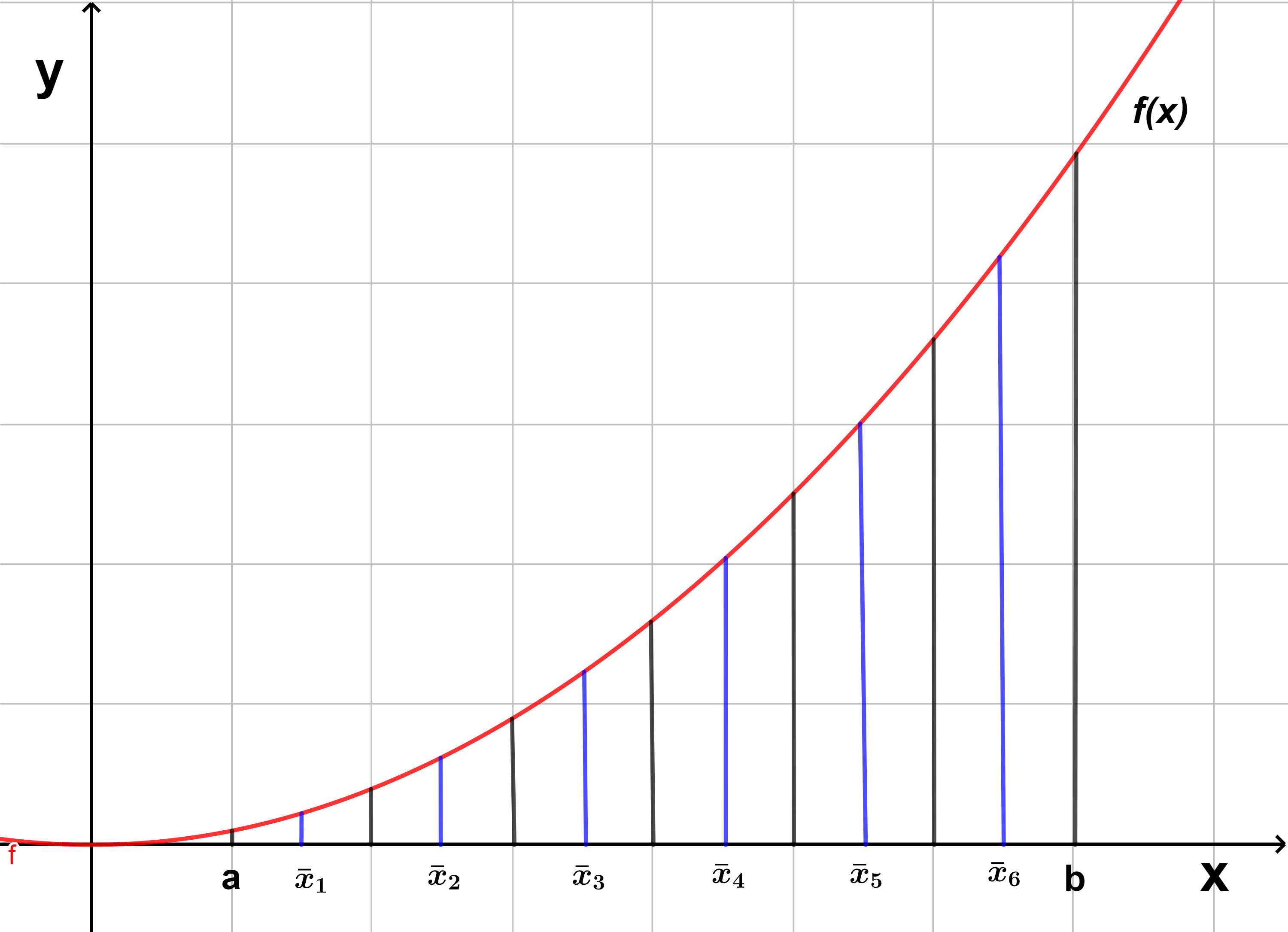
Sea una función $f(x)$ continua en un intervalo $[a, b]$. Dividimos este intervalo en $n$ subintervalos de igual longitud como se observa en la figura $1$, expresemos esta longitud como:
$$\Delta x=\frac{b-a}{n}$$
A medida que $n \to \infty$ mejor es la aproximación a la integral de la función $f(x)$.
Recordemos que la integral definida se puede aproximar como [Hipervinculo: Calculo II-Definición de la integral]
$$\int_{a}^{b}f(x)dx\approx \sum_{i=1}^{n}f(x_{i})\Delta x$$
Donde $x_{i}$ es cualquier punto en el i-ésimo subintervalo $[a, b]$. Se puede considerar a $x_{i}$ como el punto medio, denotemos este punto como $\bar{x_{i}}$, así como se muestra en la figura $1$.
Sumamos estos $n$ puntos medios evaluados sobre la función $f(x)$ multiplicadas por $\Delta x$, obtenemos una aproximación a la integral, a este método se le conoce como regla del punto medio y está definida como:
$$\int_{a}^{b}f(x)dx\approx M_{n}= \sum_{i=1}^{n}f(\bar{x_{i}})\Delta x=\Delta x\left [ f(\bar{x_{1}})+f(\bar{x_{2}})+…+f(\bar{x_{n}}) \right ] \tag{1}$$
Con:
$$\Delta x=\frac{b-a}{n}$$
Llamado tamaño de la malla y:
$$\tilde{x_{i}}=\frac{1}{2}\left ( a+b \right )$$
Es el punto medio del intervalo $[a, b]$.
Regla del trapecio
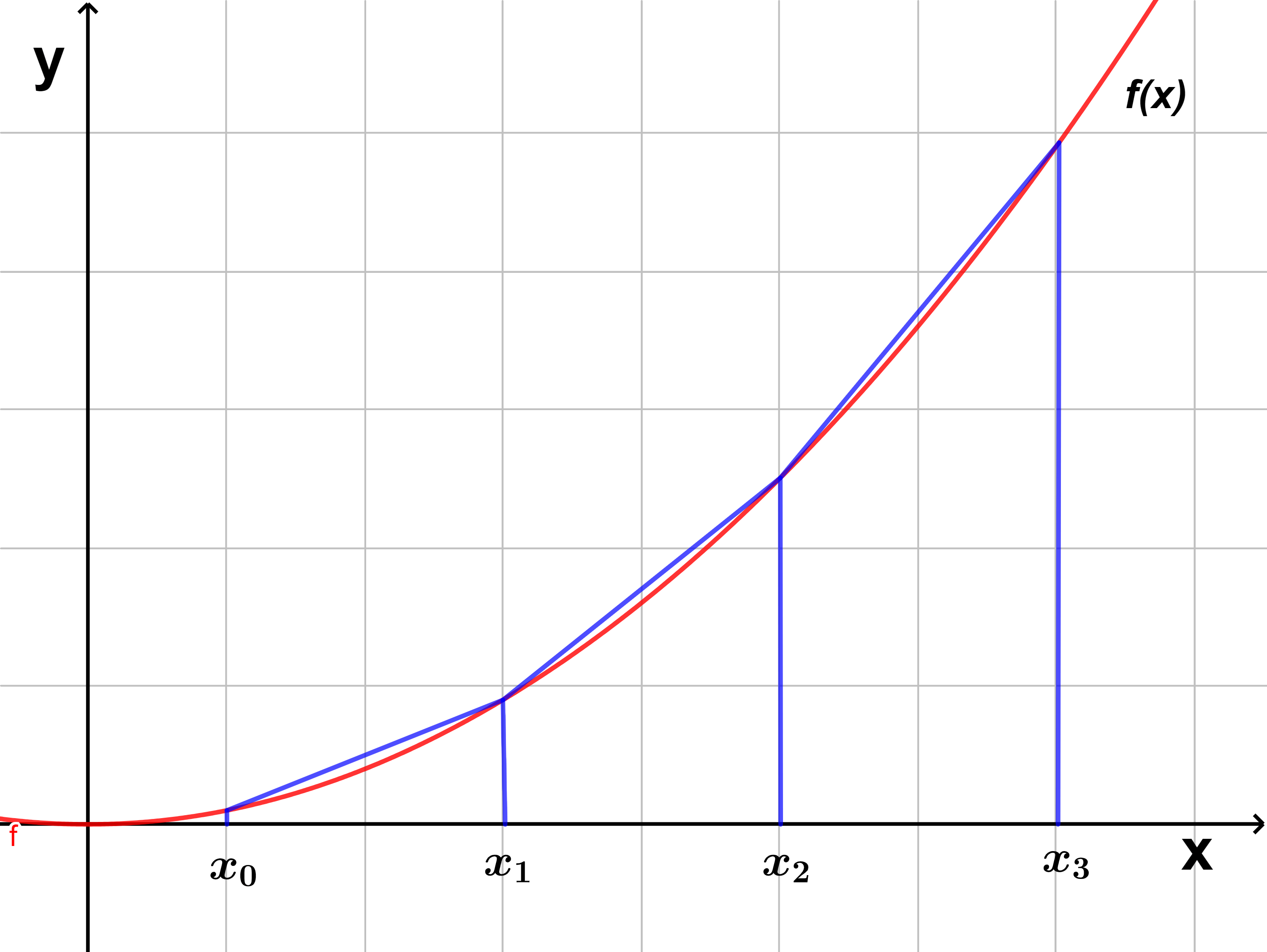
Este método consiste en considerar varios trapecios y aproximarse a la función $f(x)$ mediante estos, recordemos que el área de un trapecio es:
$$1/2 (base \space mayor + base \space menor) \space por \space altura$$
Así el área del i-esimo trapecio es:
$$A=\frac{f(x_{i-1})+f(x_{i})}{2}\Delta x$$
Análogamente, a la deducción del método de la regla del punto medio, consideremos una función $f(x)$ continua en el intervalo $[a, b]$, dividimos este intervalo en $n$ subintervalos con longitud $\Delta x=\frac{b-a}{n}$, en donde se aproxima el área de la integral por medio de trapecios como lo vemos en la siguiente imagen:
Por lo que se puede aproximar la integral de la función $f(x)$ tomando $n$ subintervalos, como:
$$\int_{a}^{b}f(x)dx\approx T_{n}= \frac{1}{2}\left [ \sum_{i=1}^{n}(f(x_{i-1})+f(x_{i})) \Delta x \right ]$$
$$=\frac{\Delta x}{2}\left [ \sum_{i=1}^{n}(f(x_{i-1})+f(x_{i})) \right ]=\frac{\Delta x}{2} \left [ f_{0}+f_{1}+…+f_{n-1}+f_{1}+f_{2}+…+f_{n} \right ]=\frac{\Delta x}{2}\left [ f_{0}+2f_{1}+…+2f_{i-1}+f_{n} \right ]$$
$$\therefore \int_{a}^{b}f(x)dx\approx T_{n}=\frac{\Delta x}{2} \left [ f_{0}+2f_{1}+…+2f_{i-1}+f_{n} \right ] \tag{2}$$
Donde:
$$\Delta x=\frac{b-a}{n}$$
Y:
$$x_{i}=a+i\Delta x$$
Cotas de error
Como son métodos de aproximación, entonces hay un error en el cual se define como la cantidad que debe ser sumada a la aproximación para llegar al valor exacto. Cuando el valor $n$ tiende a ser muy grande, el valor $\Delta x=\frac{b-a}{n}$ tiende a cero, por lo que $M_{n}$ y $T_{n}$ tienden al valor exacto de $\int_{a}^{b}f(x)dx$ pero es claro que hacerlo en papel es muy difícil de llegar al valor exacto por lo que a continuación se definen las estimaciones de las cotas de los errores:
Consideremos que $|f´´(x)|\leq K$ para $a\leq x \leq b$ , es decir, la segunda derivada de $f(x)$ está acotada por $K$, una cota superior para los valores de $|f´´|$ en $[a, b]$. Si $E_{M}$ y $E_{T}$ son los errores en la regla del punto medio y la regla del trapecio respectivamente, para $n$ pasos, entonces:
$$|E_{M}|\leq \frac{K(b-a)^{3}}{24n^{2}}$$
$$|E_{T}|\leq \frac{K(b-a)^{3}}{12n^{2}}$$
Obsérvese que $|f´´(x)|$ es el valor absoluto de la segunda derivada de la función.
Veamos un ejemplo de como se aplican estos dos métodos numéricos.
Ejemplos
- Usar la regla del punto medio y del trapecio con $n=5$ para aproximar la integral $\int_{1}^{2}\frac{1}{x}dx$ y calculé los errores respectivos.
Vemos que $n=5$, $a=1$ y $b=2$ $\Rightarrow \Delta x=\frac{2-1}{5}=\frac{1}{5}$
Comenzamos con el método de la regla del punto medio, tenemos que los puntos medios son: $\tilde{x_{i}}=\frac{1}{2}\left [ x_{i-1}+x_{i} \right ]$, como estamos en el intervalo $[1, 2]$ dividimos este intervalo en $5$, ya que $n=5$ y tendremos los siguientes subintervalos:
$$[1, 1.2], \space [1.2, 1.4], \space [1.4, 1.6], \space [1.6, 1.8] \space y \space [1.8, 2]$$
Ahora obtengamos $\bar{x_{i}}$, que son los puntos medios respectivamente de los subintervalos anteriores, los cuales son:
$$1.1, \space 1.3, \space 1.5, \space 1.7 \space y \space 1.9$$
Usando la relación $(1)$, tenemos que:
$$\int_{1}^{2}\frac{1}{x}dx\approx \Delta x\left [ f(1.1)+f(1.3)+f(1.5)+f(1.7)+f(1.9) \right ]=\frac{1}{5}\left [ \frac{1}{1.1}+\frac{1}{1.3}+\frac{1}{1.5}+\frac{1}{1.7}+\frac{1}{1.9} \right ]\approx 0.691908 \tag{3}$$
Ahora usamos el método de la regla del trapecio recordando que:
$$x_{i}=a+i\Delta x$$
Entonces:
$$x_{0}=1$$
$$x_{1}=1+(1)(\frac{1}{5})=1.2$$
$$x_{2}=1+(2)(\frac{1}{5})=1.4$$
$$x_{3}=1+(3)(\frac{1}{5})=1.6$$
$$x_{4}=1+(4)(\frac{1}{5})=1.8$$
$$x_{5}=1+(5)(\frac{1}{5})=2$$
Por ende, usamos la relación $(2)$, se tiene que:
$$\int_{1}^{2}\frac{1}{x}dx\approx \frac{0.2}{2} \left [ f(1)+2f(1.2)+2f(1.4)+2f(1.6)+2f(1.8)+f(2) \right ]=0.1\left [ \frac{1}{1}+\frac{2}{1.2}+\frac{2}{1.4}+\frac{2}{1.6}+\frac{2}{1.8}+\frac{1}{2} \right ]\approx 0.695635 \tag{4}$$
Para calcular las cotas de los errores tomemos la segunda derivada de la función:
$$|f´´(x)|=|\frac{2}{x^{3}}|$$
Como estamos en un intervalo, entonces:
$$1\leq x \leq2 \Rightarrow 1 \geq \frac{1}{x}$$
Por lo que:
$$|f´´(x)|=|\frac{2}{x^{3}}|\leq|\frac{2}{1^{3}}|\leq 2 $$
Así tenemos que una cota superior es $K=2$, de manera que:
$$|E_{T}|\leq \frac{2(2-1)^{3}}{12(5)^{2}} \approx 0.06667$$
$$|E_{M}|\leq \frac{2(2-1)^{3}}{24(5)^{2}} \approx 0.00333$$
Observemos que las cotas de error se encuentran en un intervalo al resolver las desigualdades, es decir, el valor de la cota de error para el método del trapecio está en el intervalo $(-0.06667,0.06667 )$ y la cota de error para el método del punto medio está en el intervalo $(- 0.00333,0.00333 )$.
Si hacemos la integral de manera directa tenemos lo siguiente:
$$\int_{1}^{2}\frac{1}{x}dx=0.693147…. \tag{5}$$
Comparamos los resultados $(3)$ y $(4)$ de estos dos métodos y observamos que en los dos métodos se aproximan al valor de la integral definida $(5)$ incluso para $n$ pequeñas, para $n$ mucho más grandes se espera que se aproximen mejor al valor de la integral definida.
Tarea moral
Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- ¿Para que valor de n se deben tomar a fin de garantizar que la aproximación de la regla del punto medio para $\int_{1}^{2}\frac{1}{x}dx$ sean exactas hasta dentro de 0.001?
- ¿Para que valor de n se deben tomar a fin de garantizar que la aproximación de la regla del trapecio para $\int_{1}^{2}\frac{1}{x}dx$ sean menor que $10^{-4}$?
- Utilice la regla del punto medio con n =4 para estimar $\int_{1}^{2}x^{2}dx$
- Utilice la regla del trapecio con n =4 para estimar $\int_{1}^{2}x^{2}dx$
- De una cota superior para aproximar la siguiente integral $\int_{1}^{2}e^{x^{2}}dx$
Más adelante…
En esta sección vimos dos métodos de aproximación numérica para las integrales que son el método del punto medio y el método del trapecio, el cual vimos que se pueden aproximar a la integral que deseemos, pero para lograr una mejor aproximación, en general, se utiliza lenguajes de programación como Python, C++, R, o software especializados como Mathematica o MatLab para mejorar la precisión de estos métodos facilitando el trabajo y obteniendo una aproximación que se quiera, siempre y cuando su computador lo permita. En el siguiente entrada veremos otro método de aproximación numérica llamado el método de la regla de Simpson.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral II.
- Entrada anterior del curso: Cálculo Diferencial e Integral II: Integración de funciones racionales por fracciones parciales – El blog de Leo (nekomath.com)
- Siguiente entrada del curso: Cálculo Diferencial e Integral II: Métodos Numéricos de Integración – Regla de Simpson – El blog de Leo (nekomath.com)

Exclentes apuntes , y la inclusion delo metodos de integracion numericos en el calculo basico
Gracias por la lectura y el comentario, Omar.