Factor de acumulación

En este apartado, se aborda el tema de funciones y factores de acumulación, donde se darán a conocer sus características o propiedades, su forma en que operan y algunos ejemplos de su aplicación. El factor de acumulación, es la manera a través de la cual los intereses se van creciendo, ya sea de forma lineal como lo es en el modelo de interés simple, o de forma compuesta, es decir; los intereses generan intereses, por lo que el crecimiento de éstos recursos es más rápido. Se entiende como valor acumulado como la cantidad total que se obtiene luego de que haya transcurrido un cierto periodo de tiempo.

Función de acumulación

Es aquella función que acumula una unidad monetaria, iniciando en un tiempo cero, luego de haber transcurrido un tiempo $t$, todo ésto con una tasa de interés. Tanto la tasa de interés como el periodo de tiempo, deben estar dados con la misma periodicidad, es decir, si por ejemplo: si el tiempo es anual, la tasa de interés que se esté manejando, igual debe de ser anual.

Cabe hacer mención, que hay función de acumulación para el modelo de interés simple, y hay función de acumulación para el modelo de interés compuesto.

Función de acumulación para interés simple

La acumulación simple que se utiliza en éste modelo, es aquella en la que el crecimiento de los intereses, se da de forma lineal, es decir, los intereses que se generan en un mismo periodo de tiempo, no se acumulan (no generan nuevos intereses) en el siguiente periodo. Dicha acumulación se puede calcular en cualquier momento.

La función de acumulación en este modelo de interés simple, es la función que se define como $a(t)$ que lleva un valor acumulado, luego de transcurrir un tiempo $t>0$. En este caso el capital que se va a manejar es de una unidad monetaria. Dicha función de acumulación $a(t)$ cumple que:

1. Es creciente y continua regularmente
2. En un valor $a(0)=1$
3. Si la función de acumulación va disminuyendo, para valor de $a$ con valores de $t$ crecientes, esto implica que hay un interés negativo.

Aunque puede ocurrir que haya intereses negativo, para efectos prácticos es irrelevante, para la mayoría de la situaciones.

El capital inicial que se invierte se le llama $K$ y es una cantidad mayor que cero, es decir; $K>0$.

$A(t)$ es la función monto con la que se obtiene el valor acumulado en el tiempo $t>0$ con un capital determinado $K$

Lo que se acaba de mencionar se traduce en lo siguiente:

$$A(t)=K a(t)$$

$$A(0)=K$$

Se denota la cantidad de intereses ganado durante un periodo de tiempo $t-$ésimo año, en una fecha de inversión $I_t$. Es decir:

$$I_t =A(t)-A(t-1)$$

para $t\leq 1$. Observe que $I_t$ considera el efecto del interés sobre un periodo $t$, en cambio $A(t)$ es una cantidad que se calcula en un tiempo determinado.

La función monto de acumulación que se tiene, cuando se está trabajando con un capital de un peso, es decir $K=1$, es una caso especial de dicha función de acumulación. En ambos casos, tanto la función de acumulación como la función monto se pueden usar de forma recíproca.

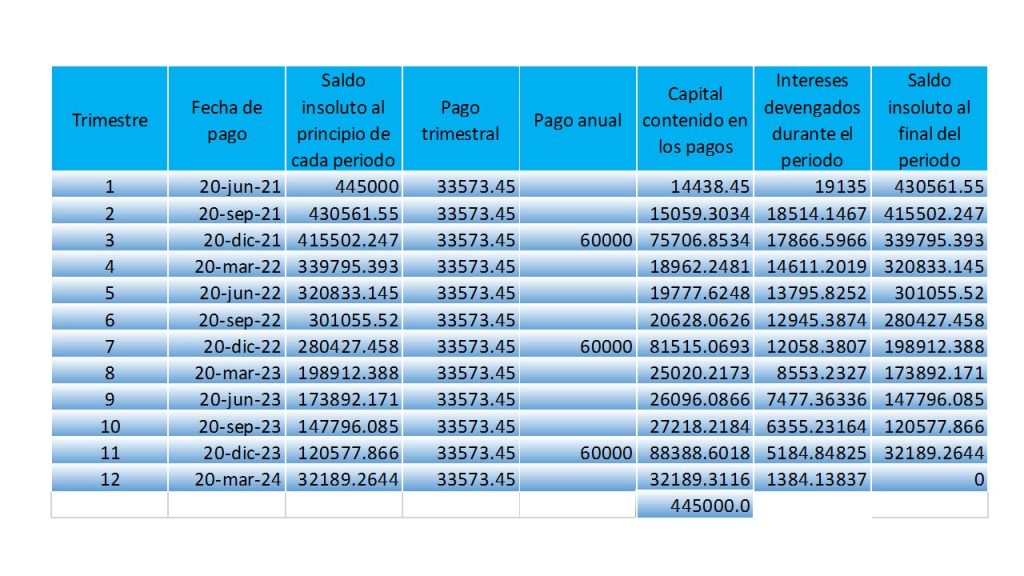
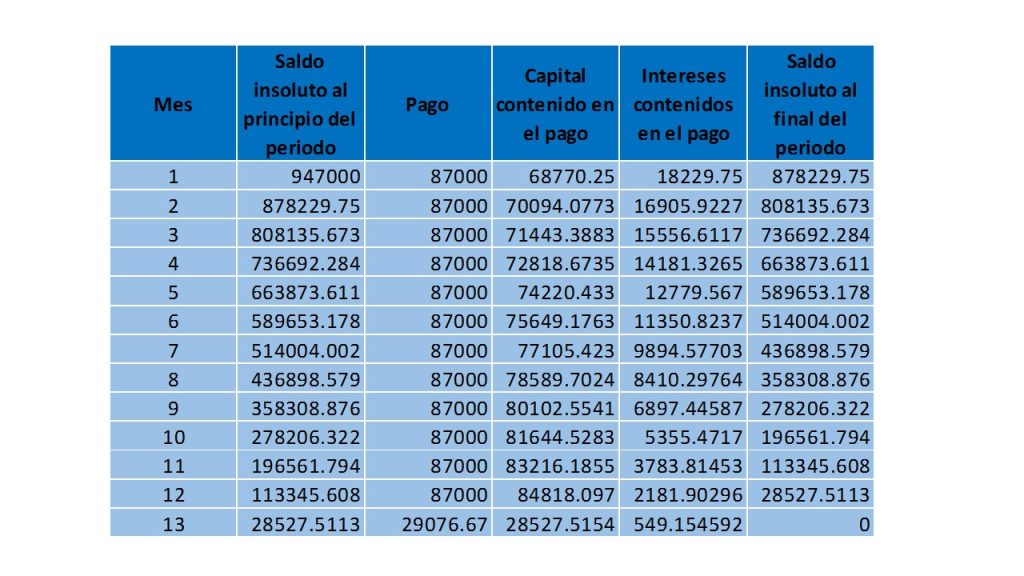
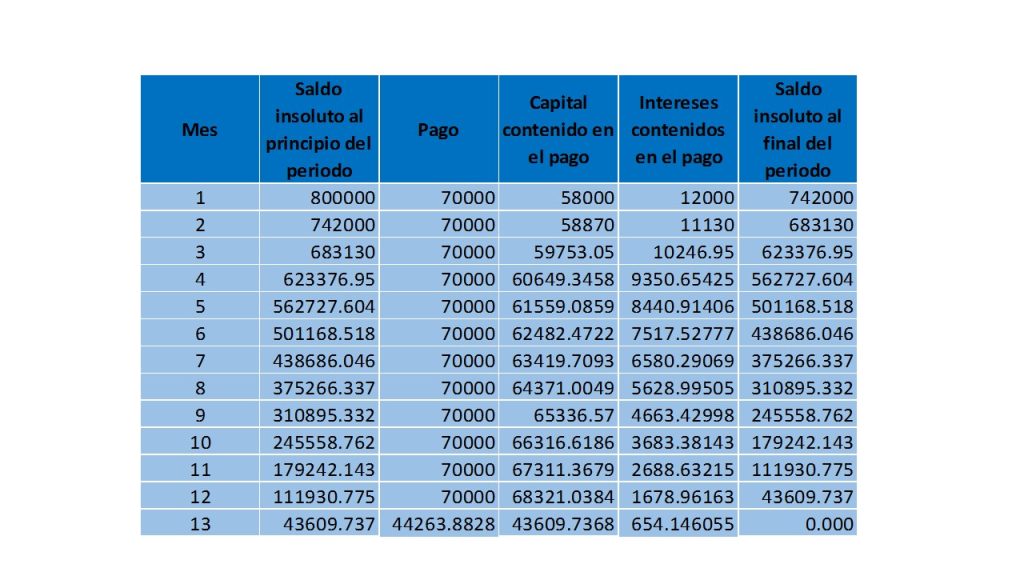
A continuación se muestran ejemplo del comportamiento de la función monto.

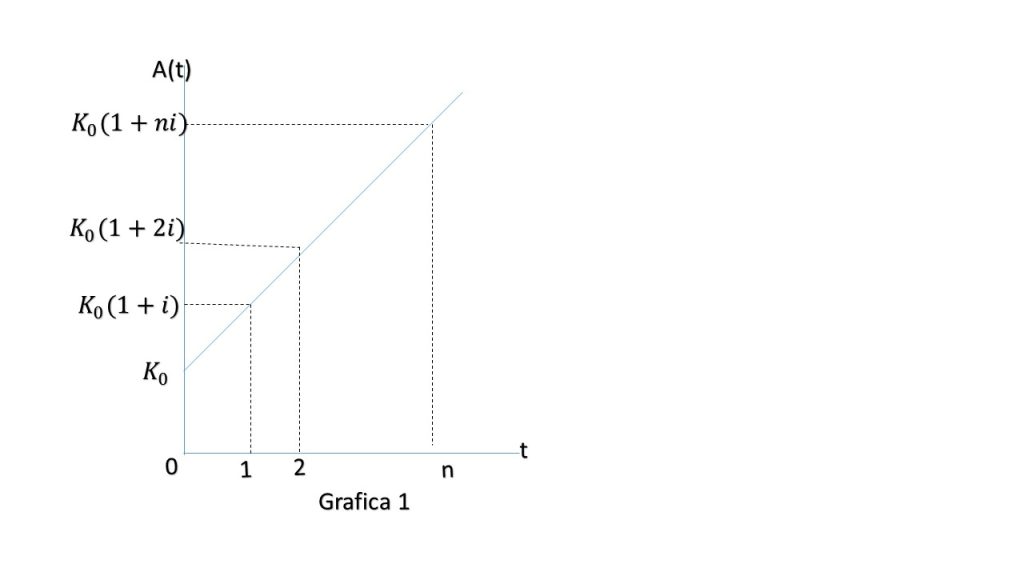
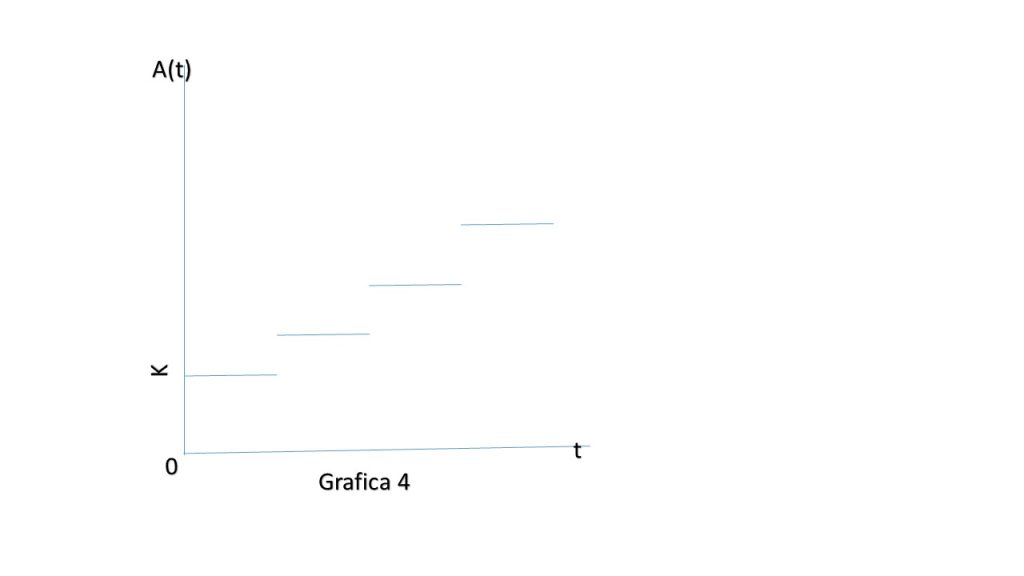
Función de acumulación para el modelo de interés compuesto

En este modelo, la función de acumulación lo intereses del capital inicial, generan intereses sobre intereses, es decir; los intereses se reinvierten ganando más intereses, por dicha característica se le conoce a este fenómeno como acumulación compuesta.

La función de acumulación, se define como la que acumula una unidad monetaria comprendido desde un momento cero, hasta un tiempo $t$ con una acumulación compuesta, y con una tasa efectiva de interés $i$, que debe coincidir con la temporalidad del tiempo, y viceversa. Dicha función es denotada por:

$$A(t)=(1+i)^t$$

Desarrollando dicha expresión de en la que está dada se comporta de la siguiente forma:

$$A(1)=1+i$$

$$A(2)=(1+i)(1+i)=(1+i)^2$$

$$A(3)=(1+i)(1+i)(1+i)=(1+i)^3$$

$$\vdots$$

$$A(t)=(1+i)^t$$

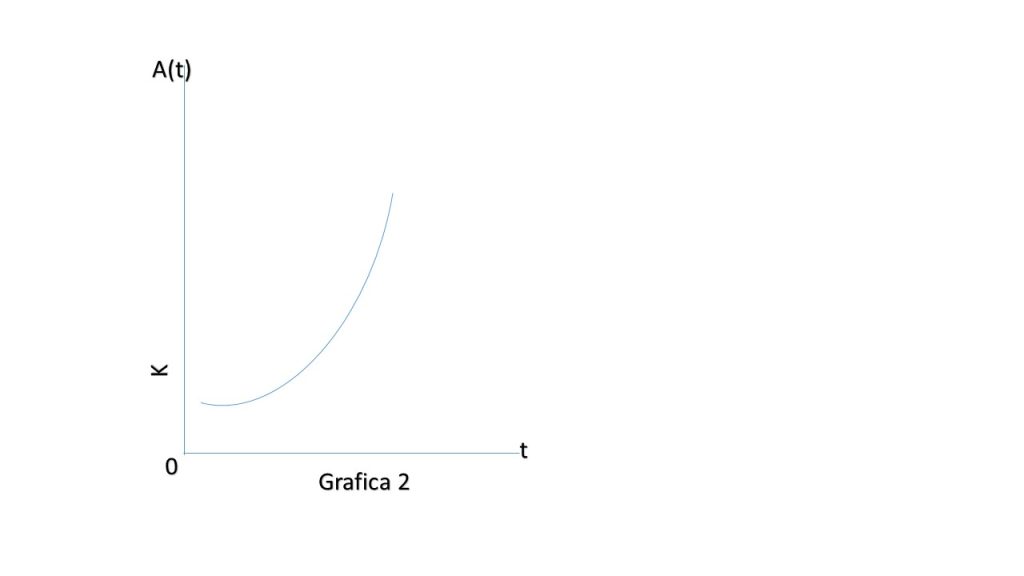
La función de acumulación es válida para toda $t$. Es importante hacer mención ya que $t$ pertenece a intervalo $t \in[0,\infty)$, se puede ampliar a $A(t)$ para comprobar que la función es válida para dicho intervalo.

Entonces, sea $t \geq 0$, y $s \geq 0$

Partiendo de $(1+i)^t$ se tiene que:

$$A(t+s)=(1+i)^{t+s}$$

$$=(1+i)^t (1+i)^s=(A(t))(A(s))$$

a dicha expresión se le aplica la definición de derivada y entonces se obtiene:

$$A'(t)=\lim_{s \rightarrow 0} \frac{A(t+s)-A(t)}{A(s)}$$

Se sustituye la expresión que se acaba de obtener de $a(t+s)$ y se obtiene:

$$A'(t)=\lim_{s \rightarrow 0} \frac{A(t)A(s)-A(t)}{A(s)}$$

$$A(t)=\lim_{s \rightarrow 0} \frac{A(s)-A(0)}{s}=A(t)A'(0)$$

$$\frac{A'(t)}{A(t)}=A'(0)$$

Aplicando propiedades de los logaritmos a la ecuación anterior, se tiene:

$$\frac{A'(t)}{A(t)}=\frac{d ln A(t)}{dt}$$

$$\frac{d ln a(t)}{dt}=A'(0)$$

En dicha ecuación se reemplaza $t$ por $n$, e integrando ambos lados, desde cero hasta $t$, se tiene:

$$\int_0^t \frac{d ln a(n)}{dn} dn=\int_0^t A'(0) dn$$

$$ln A(t)- ln A(0)=tA'(0)$$

donde $A(0)=1$ cuando $t=1$, luego entonces:

$$ln a(1)=A'(0)$$

y recordando de que $A(1)=1+i, se tiene:

$$ln (1+i)=A'(0)$$

Sustituyendo éste ultimo resultado, en $ln A(t)- ln A(0)=tA'(0)$, se da lugar a:

$$ln A(t)=t ln(1+i)=ln(1+i)^t$$

$$A(t)=(1+i)^t \forall t\geq 0$$

dicha expresión que se acaba de obtener, se puede escribir de la siguiente forma:

$$A(t)=A(0)(1+i)^t$$

Más adelante…

En las siguientes apartados se mostrara que diferentes maneras de como se pueden dar este proceso de acumulación, para fines de aplicación en la práctica real, sólo es necesario que se haga uso de 2 funciones de acumulación, que corresponde al modelo de interés simple y de interés compuesto.

Ir a Matemáticas Financieras

Entrada anterior

Entrada siguiente

Introducción

Este apartado, se presentara el concepto de tasa efectiva de interés, sus características y la forma en que se puede aplicar, tanto al modelo de interés simple como al compuesto, para evidenciar su uso.

Definición

Se entiende como tasa efectiva de interés o también tasa efectiva por periodo, a la proporción de intereses ganados por unidad de capital de tiempo. El llamarla efectivo mensual o efectiva, dentro de las matemáticas financieras, para especificar la tasa de la que se está hablando, esto es la tasa que corresponde a la que se pagará por unidad de capital y de tiempo.

Desarrollo

La periodicidad de la tasa, es la que nos va a indicar cada cuando se tienen que pagar los intereses. Éstos pueden ser pagados con la periodicidad que se desee, esto es; en años, meses, días, semanas, etc. Bastará con hacer mención que la tasa es efectiva por día, por semana, por mes, etc. Es necesario resaltar, que la tasa de interés siempre tendrá que contar con el lapso o periodicidad con la que se esté trabajando, ya que con esto se da a conocer cada cuando se harán los pagos de los intereses.

El hecho de que éste tipo de tasas se les agregue la palabra «efectiva», hace posible que se eviten confusiones con otro tipo de tasas, como las nominales, las instantáneas, las cuales se verán más adelante.

Ejercicios resueltos

Ejercicio. En el modelo de interés simple se nos pide que se calcule Los intereses generados por un capital de \$100 con una tasa efectiva mensual del 15% en un plazo de 5 meses

Ejercicio. Haciendo uso del modelo de interés simple, calcula los intereses generados por una tasa efectiva trimestral de 22%, en un plazo de 10 meses con un capital de \$500

Ejercicio. Usando el modelo de interés compuesto calcula los intereses generados por una tasa efectiva anual del 6.5%, luego de 2 años 6 meses, con un monto de \$300.

Más adelante…

Se estarán analizando los diferentes tipos de tasas con las que operan las matemáticas financieras, para conocer e identificar sus características así como sus diferencias.

Ir a Matemáticas Financieras

Entrada anterior

Entrada siguiente

Introducción

En este apartado, se abordará el tema de tasas equivalentes, el cual nos proporciona de una herramienta bastante útil, ya que nos permite poder obtener cualquier combinación posible de una tasas de interés efectiva, a una nominal o a una instantánea. En pocas palabras, cualquier combinación posible.

Definición de Tasa Equivalente

Una tasa equivalente, es aquella que genera la misma cantidad de dinero, en el mismo tiempo, dicho con otras palabras, producen el mismo efecto de acumulación, después de un tiempo determinado, sin importar la periodicidad de pago, es decir, no importa que la periodicidad de pago no sea la misma.

Reglas de aplicación

Para poder aplicar éste concepto, se hará sus de la triple igualdad, y en la siguiente imagen se muestra una descripción de todas las combinaciones posibles que se pueden realizar:

Para poder obtener tasa equivalentes hay que hacer uso del modelo de la triple igualdad

Debe cumplir que con una misma cantidad de dinero, se debe obtener el mismo monto acumulado, una vez transcurrido en el mismo tiempo, sin importar que la periodicidad de la tasa sea diferente.

Ejercicios resueltos

Ejercicio. Calcule la tasa efectiva mensual que sea equivalente a una tasa del 18% efectiva anual.

Ejercicio. Calcule la tasa nominal pagadera 4 veces al año, es decir trimestral, equivalente a una tasa efectiva anual, del 15%

Más adelante…

Se continuará abordando, temas de aplicación y combinación de herramientas como la que se vio en éste tema, para una mejor comprensión de la relevancia que van adquiriendo cada uno de los conceptos abordados.

Ir a Matemáticas Financieras

Entrada anterior:

Entrada siguiente:

Introducción

Este apartado considera algunos casos reales en los que podemos aplicar los conocimientos adquiridos a lo largo de éstas notas. Son ejemplos que nos permiten conocer qué tipo de inversiones nos convienen más, como lo es cuando queremos invertir en CETES, ante dicha situación podemos usar el conocimiento adquirido para determinar, el valor de uno de sus títulos, y poner en práctica de forma real, para conocer mejor cual es el manejo real de algunas una de las formulas, evidenciando la forma en la que se pueden utilizar de forma aplicada en alguna situación real.

Aplicación en CETES

Como se estuvo exponiendo a lo largo del desarrollo de éstas notas, las matemáticas financieras son una poderosa herramienta, que nos sirve para determinar el valor del dinero a través del tiempo. Para realizar dicho análisis, vimos una cierta cantidad de conceptos que nos permitieron comprender mejor cómo funciona el mundo de las finanzas, aspectos que la afectan como lo es la inflación, partiendo desde el ejemplo más simple de interés compuesto, hasta llegar al punto de elaborar tablas de amortización, cálculo de valor de bonos, temas en los que se combinaban una enorme cantidad de conceptos para su construcción.

En este apartado, lo que se va a realizar es, mostrar algunos ejemplos con aplicaciones reales, de los conceptos que en éstas notas se estuvieron abordando, para que se pueda tener una mejor comprensión de la importancia del uso de las matemáticas financieras, en el mundo real.

Un ejemplo práctico del uso de las matemáticas financieras, en un caso real es el siguiente:

El precio de un CETE se puede calcular, conociendo su tasa de rendimiento, o su tasa de descuento, y se obtiene utilizando la siguiente ecuación¹:

$$P=\frac{VN}{\left(1+\frac{i*t}{360}\right)}$$

donde:

P = Valor del CETE (redondeado a 7 decimales)

VN = Valor Nominal del título en pesos

i = Tasa de rendimiento

t = tiempo o plazo en días del CETE

Si $d$ es la tasa de descuento de un CETE se tiene que:

$$d=\frac{i}{\left(1+\frac{i*t}{360}\right)}$$

despejando $i$,

$$i=\frac{d}{\left(1-\frac{d*t}{360}\right)}$$

Al sustituir éste resultado en la primera ecuación se obtiene el precio de un CETE a partir de su tasa de descuento:

$$P=VN*\left(1-\frac{d*t}{360}\right)$$

Por lo que se tiene que el precio de un CETE está compuesto por el valor presente de su valor nominal.

Ejercicios resueltos

Ejercicio. El 31 de agosto del año 2000, un inversionista compra CETES con las siguientes características:

• Valor nominal: \$10 pesos
• Fecha de colocación: 31 de agosto del año 2020
• Fecha de vencimiento: 28 de septiembre del año 2020
• Días por vencer del título: 28 días

Suponiendo que está sujeto a una tasa de rendimiento anual del 15%, obtener el valor del CETE.

Ejercicio. Supongamos ahora, el siguiente caso: un inversionista compra CETES con las siguientes características:

• Valor nominal: \$10 pesos
• Fecha de colocación: 24 de marzo de 2023
• Fecha de vencimiento: 23 de junio de 2023
• Duración del título: 91 días
• Tasa de rendimiento: 4.39%

Aplicación para calcular el Costo Anual Total (CAT)

Otra aplicación bastante útil, para la que nos sirve las Matemáticas financieras, es cuando nosotros contratamos una tarjeta de crédito, y deseamos saber el costo real que vamos a tener que pagar por la línea de crédito que no otorgan, dicho en otras palabras, deseamos saber cuánto dinero nos va a costar tener a nuestra disposición dichos recursos económicos.

Primero que nada, la definición del CAT, es una forma de poder medir el total de costos y gastos que se tienen que hacer, cuando algún banco nos otorga un crédito, en este caso particular, se va a analizar el caso de una tarjeta de crédito (lo que incluye intereses, comisiones, anualidad, comisiones por apertura, gastos de investigación, seguros, etc.). La importancia de conocer ésta herramienta, nos permite comparar y poder elegir cuál es la mejor opción de banco o institución financiera que nos ofrece la opción con un menor costo.

Para poder calcular el Costo Anual Total, de acuerdo con la circular 21/2009³ emitida por el Banco de México, la metodología utilizada para calcular el CAT es la siguiente:

$$\sum_{j=1}^M\frac{A_j}{(1+i)^{t_j}}=\sum_{k=1}^N\frac{B_k}{(1+i)^{S_k}}$$

donde:

$i =$ CAT, expresado como decimal

$M =$ Número total de disposiciones de crédito

$j =$ Número consecutivo que identifica cada crédito

$A_j =$ Monto de la j-ésima disposición de crédito

$N =$ Número total de pagos

$k =$ Número consecutivo que identifica cada pago

$B_k =$ Monto del k-ésimo pago

$t_j =$ Intervalo de tiempo, expresado en años y fracciones de año, que transcurre entre la fecha en que surte efecto el contrato y la fecha j-ésima disposición del crédito

$s_k =$ Intervalo de tiempo, expresado en años y fracciones de año, que transcurre entra la fecha que surte efecto el contrato y la fecha del k-ésimo pago

$\sum =$ Símbolo utilizado para expresar la suma de las cantidades indicadas

Notemos que dentro de la ecuación que se acaba de presentar, se está usando el concepto de valor presente en la expresión $(1+i)^{t_j}$, aunque de forma general, la expresión para calcular el CAT, del lado izquierdo considerando la sumatoria, nos permite obtener la sumas del valor presente de las disposiciones del crédito.

Por otra parte, el lado derecho de la fórmula para calcular el CAT, representa la suma del valor presente de los pagos que se realizaran para liquidar el crédito. Si hacemos un pequeño recordatorio, en general la fórmula que estamos usando, tanto el lado izquierdo como el derecho, ambas en conjunto son una ecuación de valor, concepto que también, fue abordado en su momento, para explicar cómo se realizan las operaciones financieras, es decir, los derechos que tiene el deudor, deben de ser iguales a los del prestamista o acreedor.

Ejercicios resueltos

Para mostrar la forma en que se utiliza la fórmula para calcular el CAT, se propone el siguiente ejemplo³:

Un banco otorga una tarjeta de crédito al señor Luis, por una línea de crédito disponible de \$15,000 pesos, cantidad que el decide gastar, inmediatamente después de haberla recibido. La cantidad de \$15 mil pesos es el valor de $A$ que es una disposición del crédito. Dicho crédito, el señor Luis, considera pagarlo dentro de 2 años, de forma mensual mediante pagos de \$962.33, sin embargo el banco le cobra una comisión por apertura de \$100 pesos.

• Ir a Matemáticas Financieras
• Entrada anterior
• Entrada siguiente

1. Información obtenida de https://www.banxico.org.mx/mercados/d/%7B0DE0044F-662D-09D2-C8B3-4F1A8E43655F%7D.pdf ↩︎
2. información obtenida de: https://www.banxico.org.mx/elib/mercado-valores-gub-en/OEBPS/Rsc/anexo0201.pdf ↩︎
3. Información obtenida de: https://www.banxico.org.mx/marco-normativo/normativa-emitida-por-el-banco-de-mexico/circular-21-2009/%7B29285862-EDE0-567A-BAFB-D261406641A3%7D.pdf ↩︎

Introducción

En ésta sección, se continúa analizando otro tipo de anualidades y la forma en que se puede construir su respectiva tabla de amortización, considerando el caso, en el que algunas empresas, de acuerdo con su experiencia, tienen contemplado el ingreso de recursos extras, a lo largo del año.

Concepto y construcción

En la sección donde se abordó el tema de anualidades, hubo algunos casos en donde se otorgaba un crédito en el que la forma de pagarlo, el acreditado realizaba pagos en el año, pero al final de éste agregaba más pagos, ya que, por ejemplo, consideraba recursos que podía tener, por concepto de aguinaldo, prestaciones, cajas de ahorro, por mencionar algunas. Para este tipo de situaciones, la tabla de amortización que puede representar el comportamiento de los pagos de dicho crédito, en general es semejante el proceso de construcción que hasta este momento se ha estado utilizando. Con la diferencia radica en la forma en que se hacen los registros de éstos pagos extras, los cuales también se harán en un mismo periodo.

Por ejemplo: Se otorga un crédito hipotecario a una empresa de refresco, la cual quiere modernizar su planta de producción, la cantidad de dicho crédito asciende a \$445,000 , para pagar en un lapso de tiempo de 3 años, mediante 12 trimestres en los que se hará un pago de \$33,573.45, los días 20 del mes. Posterior a ése tiempo, se realizarán pagos anuales por la cantidad de \$60,000 a partir del mes de diciembre.

El contrato en cuestión, entra en operación el día 20 de marzo del año 2021, acordando una tasa de interés de 4.4% fija efectiva trimestral, la cual aplicará durante toda la duración del crédito. Los pagos se realizarán en forma vencida, por lo que el primer pago se tendrá que hacer el día 20 de junio del 2021.

La ecuación de valor que se usará para resolver este problema es la siguiente:

$$445,000=X\prescript{}{12}{\mathbf{A}}_{0.044}+60,000\prescript{}{3}{\mathbf{\ddot{A}}}_{0.18342}v_{0.043}^3;$$

de donde $X=\$33,573.45$

A continuación, se muestra la tabla de amortización en la que se agregó una columna, en la que se anotara las fechas en las que se realizaran los pagos. Observe que hay dos columnas para el registro de las fechas de los pagos una que corresponde a los pagos trimestrales, y otra para los pagos anuales, los cuales son pagos que se recibirán al final de año, por concepto de los aguinaldos que en dichas fechas recibe.

Tabla de amortización de N pagos iguales y uno desigual

Este tipo de amortización ocurre, en los casos que la empresa que solicita el crédito pacta que la cantidad de los pagos es ajustada a su posibilidad de pago, en lugar de aceptar la que ofrece la institución que otorga el crédito. En estos casos se hace uso del concepto de anualidades tomando la cantidad que propone el deudor, y la variable n la cual va a representar el número de pagos, para conocer su valor será despejada de la ecuación de valor. Como la cantidad propuesta por el deudor, puede que no tenga considerados pagos completos para cubrir el pago total del préstamo, es por esta razón que se recurre al pago desigual, con el que será liquidado por completo en el último pago, la deuda. Para poder conocer la cantidad a la asciende éste pago desigual, será obtenido a partir de una segunda ecuación de valor, basada en la original, donde ya se conocen la cantidad de pagos completos.

La construcción de la amortización, sigue compartiendo muchas similitudes a como se han venido elaborando en los temas anteriores, con la diferencia de que el último pago es diferente.

Por ejemplo: a una empresa le otorgan un crédito de \$947,000, y de los recursos que tiene por concepto de ingresos, puede disponer de la cantidad \$87,000 de forma mensual, los cuales serán destinado al pago de dicho crédito. La tasa de interés que acordaron fue del 23.1% convertible mensualmente. Para resolver éste problema, la ecuación de valor que se va a utilizar es la siguiente:

$$947,000=87,000\prescript{}{n}{\mathbf{A}}_{0.01925}$$

recordemos que el valor 0.01925, se obtiene porque se está trabajando con una tasa convertible mensual, por lo que se hace lo siguiente para poder ocuparla:

$$\frac{23.1}{12}=1.925$$

$$\frac{1.925}{100}=0.01925$$

para obtener el valor de n, se hace lo siguiente:

$$947,000=87,000\left(\frac{1-v_{0.01925}^n}{0.01925}\right)$$

$$947,000=87,000\left(\frac{1-\left(\frac{1}{(1+0.01925)^n}\right)}{0.01925}\right)$$

$$\frac{947,00}{87,000}=\left(\frac{1-\left(\frac{1}{(1+0.01925)^n}\right)}{0.01925}\right)$$

$$10.88505747=\left(\frac{1-\left(\frac{1}{(1+0.01925)^n}\right)}{0.01925}\right)$$

$$(0.01925)(10.88505747)=1-\left(\frac{1}{(1+0.01925)^n}\right)$$

$$(-1)(0.2095373563-1)=(-1)\left(-\left(\frac{1}{(1+0.01925)^n}\right)\right)$$

$$1-0.2095373563=\left(\frac{1}{(1+0.01925)^n}\right)$$

$$0.7904626437=\frac{1}{(1+0.01925)^n}$$

$$(0.7904626437)(1.01925)^n=1$$

$$(1.01925)^n=\frac{1}{0.7904626437}=1.265081921$$

$$(n)(log(1.01925))=log(1.265081921)$$

$$n=\frac{log(1.265081921)}{log(1.01925)}=12.332222$$

de dicha ecuación se nos arroja el valor de n=12.332222, lo cual se interpreta como 12 pagos por la cantidad de \$870,000 con un pago desigual, dando un total de 13 pagos. El valor del último pago, se obtiene con la siguiente ecuación:

$$947,000=87,000\prescript{}{12}{\mathbf{A}}_{0.01925}+Xv_{0.1925}^13$$

$$947,000=87,000\left(\frac{1-v_{0.01925}^12}{0.01925}\right)+Xv_{0.01925}^{13}$$

$$947,000=87,000\left(\frac{1-\left(\frac{1}{(1+0.01925)^{12}}\right)}{0.01925}\right)+X\left(\frac{1}{(1+0.01925)^{13}}\right)$$

$$947,000=87,000(10.62421639)+X(10.7804599799)$$

despejando X:

$$X=\frac{22,693.17405}{0.7804599799}$$

se obtiene el valor que estamos buscando: X=29,076.67.

A continuación, se muestra la tabla de amortización:

Ejercicios resueltos

Ejercicio. La empresa de refacciones de maquilas, quiere ampliar su planta productora, para lograrlo solicito un crédito por la cantidad de \$800,000 pesos, y de acuerdo a su experiencia de ingresos anuales, puede disponer de la cantidad de \$70 mil pesos, para hacer pagos de forma mensual, con una tasa de interés convertible bimestral del 18%. El dueño de la empresa quiere saber: ¿Cuántos pagos tendría que hacer para liquidar totalmente la deuda? y también quiere conocer su tabla de amortización.

Más adelante…

Se continuará, un poco más, abordando algunas variantes de construcción de las tablas de amortización, y ejemplificando algunas situaciones en las que se aplican, describiendo el contexto para su mejor comprensión.

• Matemáticas Financieras
• Entrada anterior
• Entrada siguiente