Introducción

En este apartado, se abordarán los orígenes que dieron lugar al nacimiento de las matemáticas financieras, las primeras operaciones en las que fueron utilizadas, la aparición del concepto de interés, la descripción de las variables y cómo fueron evolucionando a través de los años y se hablara de forma general acerca del sistema financiero mexicano, tema indispensable para poder llevar a cabo cualquier actividad económica.

Las matemáticas financieras están presentes en la vida cotidiana, tanto de empresas como de personas ya que, muchas de las actividades que se realizan a diario, y sobre todo las que tienen que ver con decisiones que involucra dinero, se llevan a cabo gracias al uso de la matemática, aunque en la gran mayoría de veces lo hagamos de forma inconsciente.

Y es que justamente la matemática, nos proporciona una gran cantidad de herramientas que nos permiten modelar, al mismo tiempo que nos otorgan información para tomar mejores decisiones, cuando nos enfrentamos a algún problema de índole económico.

Historia

El origen del concepto de interés, se puede ubicar a lo largo de la historia, desde el momento en el que, el ser humano, comenzó ha prestar sus bienes o posesiones a otro; exigiendo que se le devuelve el bien o recurso inicial, más aparte una cantidad extra.

A lo largo de miles de años y en diversas culturas como la fenicia, hebrea, griega, egipcia y china, ha sido una práctica común y equitativa recibir una compensación cuando una persona presta un bien, servicio o una suma de dinero a otra persona. Esto nos lleva a pensar que en la idea de que se tiene que hacer un pago en agradecimiento a por haber hecho uso de un bien ajeno. Este pago de compensación, a menudo denominado interés, se fundamenta en el hecho de que el prestamista está cediendo temporalmente su propiedad a favor del prestatario. Durante este período, el prestamista se priva del uso de ese bien, lo que justifica recibir una recompensa que compense esta privación.

En el Siglo XVIII, Jeremy Bentham (1748-1832) formuló la teoría utilitarista, en la que planteaba que todo individuo que prestaba un bien, también sacrificaba la utilidad de que él mismo había podido darle si hubiera decidido conservarlo. De ésta idea surge, que es razonable que al finalizar el dicho préstamo, la persona que había sido beneficiada, otorgará una cantidad extra como por haberse privado de dicho bien o recurso.

Éstas ideas fueron adoptadas por los economistas del siglo XX, en particular por Irving Fisher, el cual desarrollo la teoría del interés, en la que plantea la razón de la exigencia de intereses en la devolución de cualquier préstamo, agregando que dicha compensación no solamente se basa en la utilidad del bien, sino que también agrego la cantidad de tiempo en que fue prestado. Es decir, no sólo tenían que ver aspectos cuantitativos, sino también temporales. Es Fisher quien comienza a introducir la noción de tasas de interés.

Objetivo de las Matemáticas Financieras

El objetivo principal de las Matemáticas Financieras es desarrollar modelos matemáticos, que describan este fenómeno social que hemos mencionado. Para lograrlo, examinaremos cómo se realizan los pagos de intereses y analizaremos las variables involucradas en esta actividad, considerando cómo interactúan a lo largo del tiempo.

Definición de Finanzas

Las finanzas es un concepto que de acuerdo con la RAE, es una palabra que tiene sus orígenes del frances «finance» y significa como una obligación que asume una persona para responder a la obligación de otra. La relación que salta a la vista, es muy estrecha con el concepto de interés mencionado anteriormente. En otras palabras Finanzas se define como una rama de la economía que se enfoca en la administración científica y el desarrollo futuro de recursos que comprenden dinero, créditos y activos, con el fin de obtener un máximo beneficio y equilibrado para los dueños, socios, trabajadores de las empresas, y de la sociedad.

Sistema Financiero Mexicano

En la actualidad, para que dichas operaciones se puedan llevar a cabo, es necesario contar con un sistema que regule cada una de ellas, en ése entendido de ideas, el sistema que nos permite realizarlas de forma sana y equitativa posible. El Sistema Financiero Mexicano es el encargado de regular todas las operaciones financieras que se realizan en nuestro país. Dicho Sistema Financiero está formado por intermediarios financieros que captan, administran canalizando el ahorro y la inversión para prestarlo a quien requieren el dinero. Dentro de este sistema se encuentran también incluidas, autoridades financieras las cuales se encargan de regular, supervisar y proteger dichos recursos económicos, En otras palabras el sistema financiero mexicano, es el que se encarga de generar las condiciones necesarias para poder desarrollar cualquier actividad económica tales como producir o consumir, y que el dinero que resulta de realizar dicha actividad, pueda tener los medios para llegar a las personas que necesitan dichos recursos.

En términos formales, se define como Sistema Financiero Mexicano al conjunto de instituciones públicas, del sector gubernamental, privadas y del sector empresarial, a través de las cuales se llevan a cabo y se regulan las actividades en las operaciones de otorgación y obtención de créditos, la realización de inversiones, prestación de diversos servicios bancarios, emisión y colocación de instrumentos bursátiles y todas aquellas relativas a la actividad financiera.^*

Las personas que cuentan con dinero pero no lo necesitan en un corto plazo, son las que se encuentran en posición de poder prestarlo, de esta manera las personas que t necesitan más dinero del que poseen, ya sea porque se encuentran realizando un proyecto de emprendimiento (un negocio, poner una panadería por ejemplo), tiene la forma de poder obtenerlo, y en tal situación; se comprometen a devolver esos recursos después de un tiempo determinado con una compensación adicional. Para poder llevarlo a la practica dichas actividades, los bancos y las tasas de interés tienen un papel un importante.

El sistema financiero mexicano esta conformado por Banco de México y la Secretaría de Haciendo y Crédito Publico.

Banco de México

La función del Banco de México es promover las condiciones para que se dé un sano desarrollo de las actividades económicas, que se accesible para los usuarios y que opere en un ambiente regulado, supervisado, así como competitivo.

Su función principal es procurar la estabilidad del poder adquisitivo del dinero (cuidar que el dinero no pierda su valor, capacidad de compra), con el que se realizan cualquier actividad económica. abasteciendo de papel moneda (billetes, monedas) al país, y propiciar un buen funcionamiento de los sistemas de pago; ésta ultima se logra a través de la ejecución de políticas monetarias y cambiarias. Es importante señalar que cualquier cambio que se realice a dichas políticas tienen su afectación directa en los precios que se pactan en los mercados financieros, como las tasas de interés, que para efectos prácticos se traducen en los costos que se pagan por adquirir créditos, rendimientos que se obtienen de inversiones, regular el cobro de comisiones por parte de los bancos, por mencionar algunos.

Secretaria de Hacienda y Crédito Público (SHCP)

Coordina la regulación y supervisión de las autoridades financieras, para asegurarse que el sistema financiero mexicano funcione de manera correcta; dichas autoridades son las siguientes:

• Comisión Nacional Bancaria y de Valores (CNBV): Supervisa a todos los bancos, que cumplan con la normativa vigente, además emite los permisos para poder abrir nuevos bancos y en caso de que no cumplan con los requisitos tiene la facultad de cerrarlos.
• Comisión Nacional de Seguros y Fianzas (CNSF): Se encarga de vigilar a las instituciones de seguros y fianzas, que tengan los recursos suficientes para poder hacer frente a sus obligaciones adquiridas respectivamente. Emite los permisos para poder abrir una compañía de seguros o para cerrar a todas las que no cumplen los requisitos para operar de acuerdo con la ley.
• Comisión Nacional para la Protección y Defensa de los Usuarios de Servicios Financieros: Autoridad que protege a los usuarios del sistema financiero mexicano, por ejemplo, en caso de existir alguna queja en contra de un banco, ellos te pueden asesorar para resolver dicha situación.
• Comisión Nacional del Sistema de Ahorro para el Retiro (CONSAR): tiene la función de vigilar a las Administradoras de Fondos para el Retiro (AFORES), que son instituciones encargadas de administrar los ahorros para el retiro de los trabajadores para que después de haber trabajado por muchos años, puedan garantizar un ingreso futuro a través de su pensión.
• Instituto para la Protección del Ahorro Bancario (IPAB): Se encarga de generar un seguro de cada uno de los depósitos bancarios, es decir; si al banco le pasa algo que quiebre y tenga que cerrar, y al dinero que tengas ahorrado no le pase nada, esta protegido (hasta cierta cantidad).

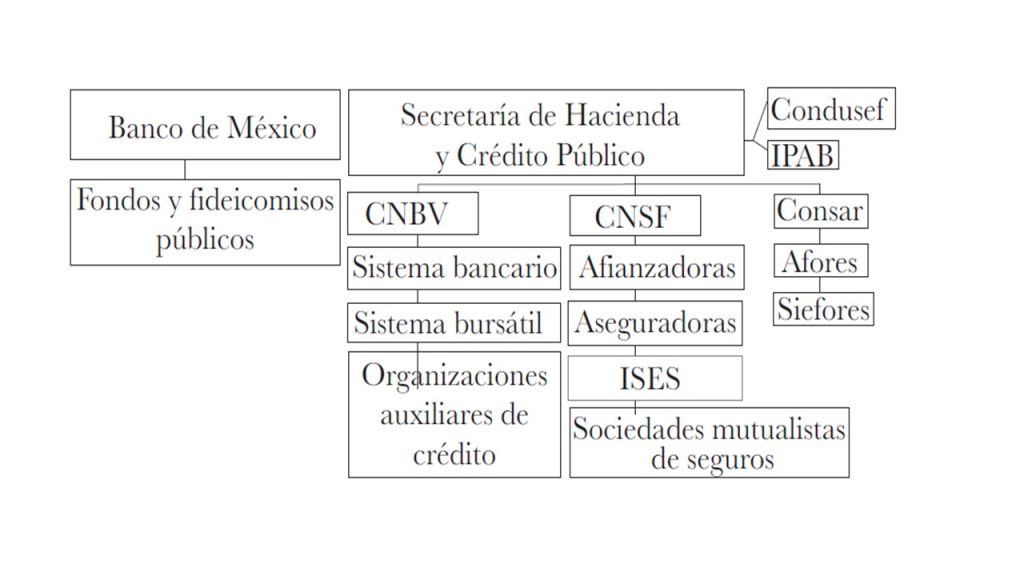
Intermediarios financieros

Son instituciones que actúan como puente entre quienes tienen dinero (ahorradores/inversores) y quienes lo necesitan (prestatarios/empresas), facilitando la realización de las actividades económicas.ofrecen servicios como depósitos, préstamos, seguros y gestión de inversiones, siendo esenciales para el desarrollo económico. Incluyen bancos, aseguradoras, casas de cambio, afores, casas de bolsa.

• Bancos: Empresas que son intermediarios entre las personas que quieren ahorrar su dinero y los clientes que quieren prestarlo.
• Aseguradoras: Se dedican a la emisión de pólizas de seguros mediante la cual, ofrecen cubrir gastos imprevistos como daños algún bien (seguro de auto) o la salud (seguro de gastos médicos), a cambio de una cantidad de dinero conocida como prima.
• Casas de cambio: Es el lugar donde se puede adquirir otras divisas (dinero de otro país) o cambio de moneda a pesos mexicanos. Por ejemplo si quieres salir de viaje y necesitas dolares, entonces acudes a una cas de cambio y puedes cambiar los pesos mexicanos en dolares.
• Afores: Como ya se menciono, son las instituciones encargadas de administrar los ahorros de los trabajadores para que en un futuro puedan vivir de ellos a través de una pensión
• Casa de Bolsa: Es la institución que se encarga de llevar a cabo la compra y venta de acciones, así como de otros instrumentos financieros. Es mediante este proceso que las personas pueden hacer inversiones mediante la compra de acciones lo que les da derecho a tener un porcentaje de las utilidades que genere la empresa.

La importancia que tiene abordar estos temas, radica en el hecho que porque el dinero nos conecta como sociedad ya que todos los días lo usamos para poder solventar nuestras necesidades; y saber como funciona el sistema financiero nos ayudara mucho para poder determinar estrategias sanas de consumo de productos, bienes, servicios, créditos, etc. Entender como funciona el dinero como medio de pago, de ahorro, permite conocer los puntos de mejora en las finanzas personales de cada individuo, así como identificar las fortalezas y oportunidades para un mejor manejo.

En el siguiente link se puede consultar el organigrama completo del sistema financiero mexicano: chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://www.gob.mx/cms/uploads/attachment/file/23187/Estructura_del_Sistema_Financiero_Mexicano_2015.pdf

*Obtenido de Marco Jurídico de las Finanzas, Quintana Adriano, Instituto de Investigaciones Jurídicas, UNAM, https://archivos.juridicas.unam.mx/www/bjv/libros/11/5140/16.pdf

Más adelante…

Se abordara el concepto de interés simple, su construcción del modelo matemático que lo describe, así como las variables que interviene y la forma en que se aplica.

Ir a Matemáticas Financieras

Ir a Interés Simple

Introducción

En la mayor parte de las operaciones financieras, son basada en hacer pagos por cierta cantidad de dinero, denominada interés, a cambio de hacer uso de dichos recursos económicos. En la mayoría de los bancos, muchos recursos surgen a partir de ésta idea que se acaba de mencionar, muchos de los ingresos que tienen los bancos son generados por el cobro de intereses que generan préstamos otorgados a los clientes.

Desde un punto de vista económico, el concepto de interés, se puede interpretar como el precio que tiene el dinero en el tiempo, es decir, es el costo que se tiene que pagar, por tener acceso de forma anticipada, a ésos recursos económicos.

Como se puede observar, se han citado varios ejemplos de actividades financieras, en las que se muestra, el hecho de pagar una cantidad de dinero, que se definió como interés, por hacer uso de una cantidad de dinero que no se tiene aún. En general todas la actividad financiera, están relacionadas con éste concepto, que tiene que ver con la cantidad de dinero que se produce en cierto tiempo, y que más adelante se le irán adjudicando diferentes conceptos relacionados, como por ejemplo, inversión, rendimiento, ganancias, etc.

Definición de interés

Se puede definir al interés, como el pago o compensación que da una persona, a cambio de hacer uso de un bien o dinero, solicitado en calidad de préstamo, durante un cierto tiempo.

El interés será denotado por la letra $I$, y para fines prácticos, se entenderá como la cantidad de dinero pagada, por haber hecho uso de una cantidad económica denominada como capital (mejor conocida como préstamo). Dicho capital será representado por la letra $K$. cuyo valor se irá incrementando de acuerdo con el valor que vaya adquiriendo $I$.

Como ya se menciono, el interés es el pago que se realiza por hacer uso del dinero. De la necesidad de tener una metodología para calcular los intereses es que comenzaron a surgir las matemáticas financieras. Podemos decir que toda operación financiera esta basada en el concepto de un préstamo, en el que hay como mínimo 2 personas involucradas el prestamista que entrega los recursos a un prestatario que es, quien recibe dicha cantidad de dinero, y que luego de haber transcurrido una cierta cantidad de tiempo, devuelve la cantidad recibida inicialmente más una cantidad por concepto de compensación.

Variables que intervienen en el concepto de interés

En una operación financiera, se entiende como interés a la diferencia que hay entre lo que se devuelve y lo que se presta. Para éstos efectos se enuncian a continuación las variables que intervienen en éste fenómeno.

1. $K=$ Es el capital inicial, o el dinero prestado
2. $M=$ Es el dinero final, o capital devuelto
3. $I=$ Interés

De tal forma que para conocer el valor de $I$ se hace lo siguiente:

$$I=M-K$$

En dicha ecuación que se acaba de citar, se muestra la relación que hay entre las variables de capital, monto e interés.

Hay algunas ocasiones en las que se va a requerir calcular cuál es el interés que se cobra por unidad de tiempo, concepto que nos conduce a definir lo que es una tasa de interés, misma que sera denotada por $i$.

En una operación financiera, la tasa de interés $i$, es la proporción que por unidad de capital y de tiempo, habrá de pagarse, por haber disfrutado de un préstamo.

Dicha tasa está dada en tanto por ciento, y siempre se debe especificar su temporalidad o periodicidad, con la cual se va a pagar.

Ejercicios resueltos

Ejercicio. Luis González hace un depósito en el banco por la cantidad de \$20,000, luego de haber transcurrido 30 días, hay en su cuenta la cantidad de \$23.500. ¿Cuánto es la cantidad de interés que le otorgo el banco?

Ejercicio. Una empresa solicita un préstamo a un banco, por la cantidad de $400,000, durante 5 años, al término de dicho tiempo, la empresa tiene que devolver la cantidad de \$500,000. ¿Cuánto es el interés que ésta pagando?

Más adelante…

Se presentan los temas de interés simple, y de interés compuesto que complementarán los conceptos que en éste apartado fueron abordados, así como sus características y las reglas que los rigen.

Ir a Matemáticas Financieras

Ir a entrada anterior

Ir a entrada siguiente

Introducción

En este apartado se abordará el primer método para valuar proyectos de inversión, es conocido como Tasa Interna de Retorno, y tiene sus bases en el modelo de interés compuesto, que ya se han venido utilizando anteriormente.

Método de la Tasa Interna de Retorno (TIR), para valuar proyectos de inversión

La Tasa Interna de Retorno (TIR), es la tasa de interés, con la que los flujos de valor presente se hace cero, en otras palabras, es la tasa que hace que los ingresos y los egresos sean iguales.

Regularmente la ecuación de valor que se utiliza, describe los flujos de un proyecto de inversión y es de grado mayor que 2, motivo por el cual la TIR, es calculada por medio de un proceso iterativo (de repetición).

En dicha ecuación, se reflejan las bases del cálculo de la tasa interna de retorno, y de la valuación de proyectos de inversión:

$$M=K(1+i)^t$$

de este modelo surge la siguiente ecuación:

$$0=M-K(1+i)^t$$

ó bien,

$$0=M-Kv^t$$

En ambos modelos, la tasa de interés que hace 0 la diferencia entre la cantidad invertida menos la recibida, es lo que se conocerá como tasa de rendimiento de la inversión.

En los proyectos de inversión, en los que no se conoce la cantidad que se va a invertir, la tasa de interés, el plazo, los flujos de la misma, los proyectos de inversión de obras o negocios (tales como obras, adquisición de maquinaria, compra de patentes, modernización tecnológica, etc.), dichos flujos deben ser calculados específicamente para el proyecto del que se esté valuando, una vez obtenidos, calcular el valor presente y su respectiva tasa de interés que vuelve cero la ecuación.

El procedimiento para hacer la valuación es el siguiente:

1. Calcular los ingresos y egresos, que se estén considerados para obtener y para invertir del proyecto, para cada uno de los periodos que dure el proyecto.
2. Obtener el valor presente de los flujos netos (ingresos – egresos) a una cierta tasa.
3. Determinar la tasa interna de retorno (y/o algunos otros indicadores como la TIR ajustada), el periodo de recuperación, la rentabilidad contable media, y el índice de rentabilidad.

Algunas reglas para su uso

1. El cálculo de los ingresos así como de los egresos, debe de hacerse basándose en estudios de mercado (precios y cantidades), costo de las construcciones y maquinaria, duración de las máquinas, su tiempo de vida, tiempos de instalación, de mantenimiento, además; de considerar el capital de trabajo que se necesitara para operar.
2. Determinar la periodicidad de los «cortes» que sea acorde a la duración del proyecto.
3. Hacer uso de una tasa adecuada para determinar el valor presente neto.
4. Ser cuidadoso al interpretar el manejo de las TIR’s no calculables o de varios valores.
5. Tener cuidado con proyectos que consideren inversiones posteriores, las cuales arrojen flujos negativos.
6. La aceptación o rechazo de la TIR dependerá de su tamaño. En general si la TIR es mayor que la tasa de referencia que se esté usando (como por ejemplo, tasa CETE o alguna otra), el proyecto se acepta, si es menor, entonces el proyecto se rechaza.
7. El inversionista puede solicitar, para algún proyecto cualquiera, que se calcule una prima de riesgo por que involucra al proyecto mismo. Dicha tasa se convierte en una «sobretasa» que se suma a la tasa de referencia. Su tamaño dependerá del tamaño del riesgo, a mayor riesgo, mayor tasa.
8. La tasa de rendimiento que espera tener el inversionista se compara contra la que arroja la valuación del proyecto.
9. Hay casos en los que la TIR no puede ser calculada, o puede tener varios valores. En dichas situaciones el analista deberá revisar los flujos, y en caso de ser necesario, partir el proyecto en varias etapas, para valuar por separado cada uno, obtener las TIR’s y luego de eso, poder tomar la decisión que corresponda.

Si la tasa de rendimiento esperara es > que la TIR, entonces se rechaza

Si la tasa de rendimiento esperada es < que la TIR, entonces se acepta.

Es importante señalar que la TIR se calcula por iteraciones tomando como base los flujos netos a los precios del periodo que corresponde.

Las tasas de cada iteración arrojan un determinado VPN, la TIR es la tasa a la que el VPN es igual a CERO. La TIR debe de tener una periodicidad de una tamaño que cada de los periodos.

Ejercicios resueltos

Ejercicio. A continuación, se quiere calcular la TIR del proyecto de inversión en una planta armadora de equipo electrónico, con los siguientes registros:

Ejercicio. Se tiene un proyecto de inversión, para el cual se tuvo el registro que muestra los siguientes flujos de efectivo:

1. Inversión inicial de 5000 pesos
2. El proyecto en cuestión ofrece tener un ingreso de 3000 pesos en el primer año, 3500 en el segundo año.

Se desea conocer la TIR, y determinar si el proyecto es viable

Más adelante…

Se continuaran abordando, diferentes formas de combinar cada una de las herramientas que se van adquiriendo en cada apartado, con la finalidad de poder evidenciar su aplicación, así como sus respectivas reglas para utilizarlas.

Ir a Matemáticas Financieras

Entrada anterior

Entrada siguiente

Introducción

En éste apartado se abordará otra metodología para valuar proyectos de inversión la cual es conocida como Valor presente neto, que como su nombre lo indica, consiste en determinar el valor presente de los flujos.

Método del Valor Presente Neto

Consiste en obtener el valor presente de los flujos de efectivo netos, con una cierta tasa esperada de rendimiento. Dicha tasa, queda determinada o pactada por el inversionista, en base a sus aspiraciones que tenga sobre el negocio, Para ello pueden hacer uso de tasas de referencia como el CETE, la TIIE, etc.

Procedimiento

1. Determinar el flujo neto así como, calcular los flujos de ingreso y de egresos.
2. Obtener el valor presente de todos los flujos netos usando la tasa de rendimiento esperada.
3. Realizar la suma de todos los valores presentes para obtener el Valor Presente Neto del proyecto de inversión.

Criterio:

Si el Valor Presente Neto es igual o mayo a cero, entonces aprueban el proyecto

Si el Valor Presente Neto es negativo, es decir; menor que cero, entonces se rechaza el proyecto.

$$VPN=F_1(1+i)^1+F_2(1+i)^2+…+F_n(1+i)^n$$

o también se puede expresar como:

$$VPN=\sum_{j=1}^nF_j(1+i)^{-j}=\sum_{j=1}^nF_jv_i^j=\sum_{j=1}^nF_j(1-d)^{j}$$

donde:

$VPN =$ Valor Presente Neto

$F_j=$ Flujo de efectivo del periodo $j$-ésimo

$i=$ tasa de rendimiento a la que se descuentan los flujos

$v=\frac{1}{(1+i)}$

$d=$ tasa de descuento equivalente a $i$

$n=$ número de años del proyecto

Reglas para su aplicación:

1. Hay proyectos de inversión, en los que la fecha de inicio es a fin de año, lo cual puede ocasionar que la ecuación del modelo que estamos usando, comience en la potencia cero, es decir: $v^0$
2. Cuando se tengan proyectos donde los flujos terminen en el año $n$, se considera que dicho plazo corresponde a la vida útil del proyecto. Sin embargo, los proyectos puede ocurrir que los proyectos continúen por más años.
3. Para los casos en los que ocurre que los proyectos continúan existiendo por más tiempo, para calcular el VPN total, se determinan los ingresos y egresos para los años siguientes (regularmente se establece un flujo fijo), es decir; se obtiene su calor presente y se le suma al VPN calculado en la primer instancia.

$$VPNT=\sum F_jv^n+\sum F_kv^{m+n}$$

lo anterior, con flujos de efectivo para cada año después del $n$

$$VPNT=\sum F_jv^n+\sum \frac{Fc}{i}v^{n}$$

la expresión anterior, con flujos iguales para cada año, después del $n$

Cabe hacer mención que hay una variante del método del VPN, el cual se llama Valor Presente Ajustado (VPA), el cual se obtiene restando al VPN el costo de oportunidad al capital que se invirtió.

$VPA=VPN-$ costo de oportunidad

El costo de oportunidad, se entenderá como «la pérdida o costo» que se incurre al haber seleccionado la opción «X» en lugar de la opción «Y». Dicho costo de oportunidad se calcula valuando los flujos de efectivo, que se obtendrían de haber invertido los recursos en un instrumento bancario de renta fija.

Ejercicios resueltos

Ejercicio. En el siguiente ejercicio tenemos el siguiente planteamiento: Un inversionista destino sus recursos al siguiente proyecto de inversión en una empresa que se dedica a armar equipo electrónico, de la cual obtuvo los siguientes registros y desea calcular el Valor Presente Neto de dicho proyecto.

Ejercicio. A continuación se muestran flujos de efectivo de un proyecto de inversión,De acuerdo a la siguiente lista:

0. -1000, en el periodo

1. se registra una cantidad de 100,
2. se registra una cantidad de 200
3. se registra una cantidad de 700
4. se registra una cantidad de 700

Y el inversionista quiere saber, por medio del método del Valor Presente Neto, si dicho proyecto le conviene

Más adelante…

A lo largo de este material se continuara abordando otros métodos para valuar proyectos de inversión, con la finalidad de evidenciar su importancia, así como la forma en que deben de utilizarse en la práctica real.

Ir a Matemáticas Financieras

Entrada anterior

Entrada siguiente

Introducción

En éste apartado, se abordará un tema importante dentro de las Matemáticas Financieras, ya que nos provee de un panorama general, sobre como podemos hacer uso de éstas, para poder aplicar los conocimientos adquiridos; en el sentido de que se mostrará como realizar análisis de proyecto de inversión. Se partirá realizando una descripción de lo que se entiende como proyecto de inversión, estableciendo sus características, así como sus alcances, las variables que intervienen, así como, algunos modelos que podemos usar y sus reglas para su aplicación.

Definición de proyecto de inversión

Un proyecto, es un modelo sistemático que define y engloba un conjunto de acciones, así como la forma en que se deben de llevar a cabo para alcanzar determinadas metas u objetivos. En dicho modelo se establecerán la forma, los recursos necesarios que se vayan a utilizar, para poder llevarlo a cabo de manera satisfactoria.

La palabra inversión, es un término que se utiliza para definir ahorro, o colocar recursos económicos que se ponen en un lugar determinado, con el fin de obtener algún beneficio que incremente la cantidad inicial después de cierto tiempo, como por ejemplo aumentar una cantidad de dinero, ganando intereses. En términos de dinero, sería gastarlo o utilizarlo de otra manera.

Por lo anterior, se entenderá como proyecto de inversión como el conjunto de elementos o variables necesarias para alcanzar una meta o un fin de índole económica, el cual consiste en esencia, en manejar, utilizar, o una cierta cantidad de recursos financieros, de una forma diferente a la que usualmente se viene realizando, para poder obtener un mejor beneficio de recursos económicos.

Es pertinente señalar que la definición antes mencionada, implica que se debe de tener al menos una diferente opción a la que se viene manejando. Dicha opción debe de contar con ciertas características, en términos de dinero destacan: productividad, rendimiento, e interés.

El objetivo que tiene la evaluación de proyectos de inversión, es el de establecer y determinar si dichas opciones que se tienen para invertir los recursos económicos, es mejor, igual o peor que la que actualmente se tiene.

Características de los proyectos de inversión

Partiendo de la definición de proyecto de inversión, se puede identificar que hay inversiones de índole puramente financiera que tienen la finalidad de obtener una ganancia o utilidad mayor. También existen proyectos de inversión que tiene que ver con algún tipo de obra, ya sea de tipo arquitectónico, físico, adquisición de programas de cómputo, patentes, adquisición de maquinaria, adquisición de una empresa o parte de ella, etc.

Ambos casos se pueden valuar, y se puede apreciar que las dos tienen como objetivo principal, un beneficio económico, un tipo de recompensa. En la mayoría de los casos, dichas valuaciones se pueden llevar a cabo mediante, la comparación de una tasa de interés emitida por una banco X, con respecto a la que emite un banco Y.

Con respecto segundo caso de la valuación de proyectos de inversión que tienen que ver con obras o adquisición de empresas, etc. dicha valuación, es más complicada de llevar a cabo, ya que involucra aspectos más complejos porque tiene que ver con tiempos más largos, dentro de los cuales, hay flujos de recursos de entrada y salida. Para éstos tipos de casos es que se han desarrollado varias metodologías.

Objetivos de los proyectos de inversión

El objetivo principal de los proyectos de inversión es el de poder determinar la tasa de rentabilidad que ofrece un proyecto de inversión, para que con ésa información se pueda tomar mejores decisiones, como por ejemplo: tener el conocimiento para invertir en la opción que ofrezca el mayor rendimiento, no invertir en proyectos que no tengan rentabilidad o sea mínima, o bien poder determinar los aspectos que afectan o favorecen dicha rentabilidad.

La valuación de proyectos de inversión nos permite también, poder conocer en qué tiempo vamos a poder recuperar la inversión que se haya realizado.

Es pertinente hacer mención que dentro de éste apartado se abordarán las metodologías que para valuar proyectos de inversión en los que no se tiene considerada de forma explícita variables de riesgo.

Algunos ejemplo en los que se tiene garantía para recuperar la inversión realizada serían:

Los depósitos bancarios a cierto plazo, como los siguientes:

• El banco «Mi ahorro», ofrece una tasa de interés del 5.4% anual, y el banco «Le money» ofrece una tasa del 7.8% anual. En éste caso se selecciona al banco «Le money» como la mejor opción para hacer la inversión.
• El banco «X» ofrece una tasa de rendimiento del 1.1715% efectiva mensual. Así mismo, el banco «Y» ofrece una tasa de interés del 15% efectiva anual.
  Para poder determinar cuál es la opción en la que más conviene hacer la inversión, lo que se tiene que hacer es calcular la tasa equivalente del 15% efectiva anual, con respecto a la tasa del 1.1715% pagadera diaria.
  En este caso tenemos que al efectuar el cálculo para obtener la tasa equivalente, llegamos a la conclusión de que es la misma tasa, por lo que, cualquiera de los dos bancos es viable para hacer la inversión.

Ejercicios resueltos

Ejercicio. El banco Alfa, ofrece una tasa de interés del 7.4% pagadero diario, mientras que el banco Beta, ofrece una tasa de interés del 7.4% efectivo anual. ¿Qué opción es la que mas conviene invertir?

Más adelante…

En el siguiente apartado se continuarán revisando más metodologías para valuar proyectos de inversión, específicamente la TIR, se definirán sus características, sus reglas de aplicación y se establecerá la relación que hay entre costo y beneficio.

Ir Matemáticas Financieras

Entrada anterior:

Entrada siguiente: