Introducción

Anteriormente definimos la integral de una función medible no negativa general, sin embargo, comentamos que existían dificultades técnicas a la hora de ver que $$\int (f+g) \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda+\int g \ \mathrm{d}\lambda.$$ (Algo bastante deseable a la hora de integrar).

En esta entrada enunciaremos y probaremos el Teorema de la Convergencia Monótona de Lebesgue, una de las herramientas más importantes en teoría de integración. Veremos también algunas de sus consecuencias, entre ellas la aditividad de la integral.

El teorema de la convergencia monótona

Teorema (de Convergencia Monótona de Lebesgue). Sea $\{f_k \}_{k=1}^{\infty}$ una sucesión creciente de funciones medibles no negativas sobre $\mathbb{R}^n$: $$0\leq f_1\leq f_2\leq f_3\dots$$ Entonces $$\lim_{k\to \infty}\int f_k \ \mathrm{d}\lambda=\int \left( \lim_{k\to \infty} f_k \right) \ \mathrm{d}\lambda$$

Demostración. Definamos $f=\lim_{k\to \infty} f_k$. Observa que $f$ está bien definida pues en cada punto es el límite de una sucesión creciente. Es medible al ser límite de funciones medibles.

Para todo $k$, claramente $f_k\leq f_{k+1}\leq f$, de donde $\int f_k \ \mathrm{d}\lambda \leq \int f_{k+1} \ \mathrm{d}\lambda \leq \int f \ \mathrm{d}\lambda$. Es decir, la sucesión $\{ \int f_k \ \mathrm{d}\lambda \}_{k=1}^{\infty}$ es creciente y acotada por $ \int f \ \mathrm{d}\lambda$. Como cualquier sucesión creciente (de números extendidos) converge a su supremo, concluimos que:

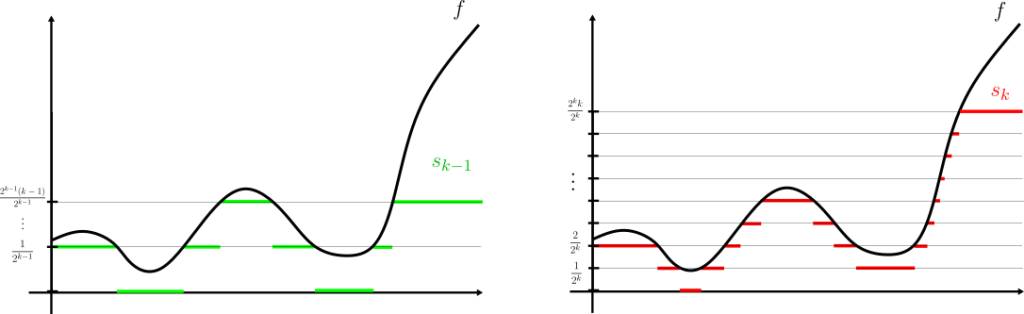
$$\lim_{k\to \infty} \int f_k \ \mathrm{d}\lambda = \sup_k \int f_k \ \mathrm{d}\lambda \leq \int f \ \mathrm{d}\lambda .$$ Veamos la desigualdad opuesta. Para ello es suficiente probar que para cada núemro real $c<\int f \ \mathrm{d}\lambda$, se tiene $c\leq \lim_{k\to \infty} \int f_k \ \mathrm{d}\lambda$. Fijemos entonces algún $c<\int f \ \mathrm{d}\lambda$. Por definición de $\int f \ \mathrm{d}\lambda$, existe alguna función simple $s\in S$ tal que $0\leq s \leq f$ y $c<\int s \ \mathrm{d}\lambda$.

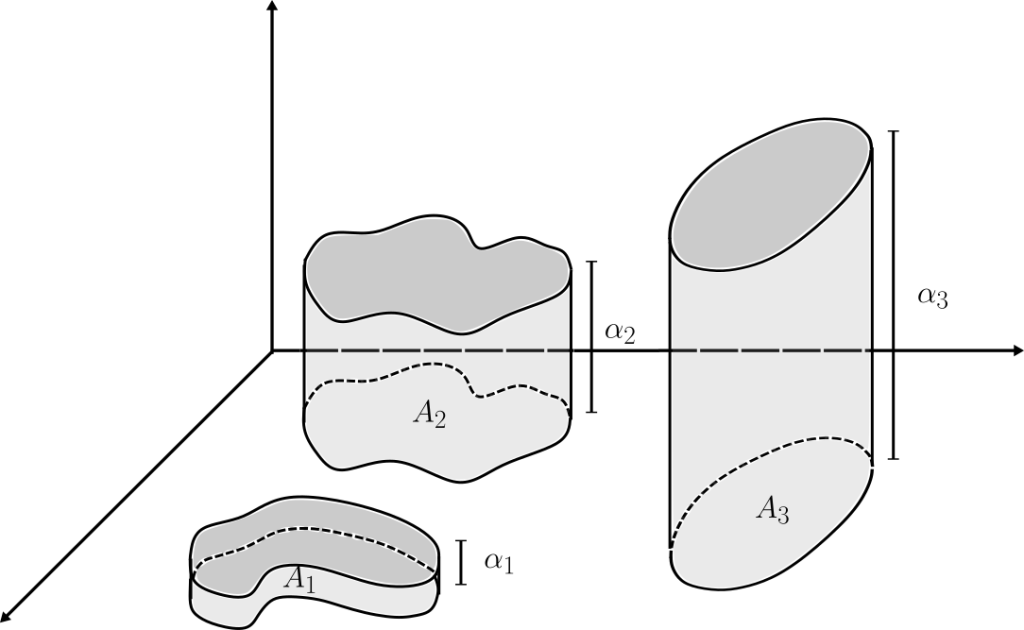
Al ser una función simple, $s$ admite una representación de la forma: $$s=\sum_{j=1}^{m}\alpha_j\chi_{A_j}.$$ Donde $0<\alpha_j<\infty$ y los conjuntos $A_j$ son medibles ajenos. Dado $\varepsilon<\min(\alpha_1,\dots, \alpha_m)$, consideremos la función simple: $$s_\varepsilon=\sum_{j=1}^{m}(\alpha_j-\varepsilon)\chi_{A_j}$$ Claramente $s_\varepsilon \in S$. Más aún, podemos escoger $\varepsilon$ suficientemente pequeño tal que $c<\int s_\varepsilon \ \mathrm{d}\lambda$: Esto es obvio si alguno de los $A_j$ tiene medida infinita. Si todos los $A_j$ son de medida finita, esto es consecuencia de la continuidad de $\int s_\varepsilon \ \mathrm{d}\lambda=\sum_{j=1}^{m}(\alpha_j-\varepsilon)\lambda(A_j)$ respecto a $\varepsilon$.

Reemplazando a $s$ por $s_\varepsilon$ de ser necesario, podemos entonces asumir que $s$ satisface:

• $0\leq s \leq f$,
• Si $f(x)>0 \ \implies \ s(x)<f(x)$,
• $c<\int s \ \mathrm{d}\lambda$.

Definamos ahora los conjuntos $$E_k = \{ x\ | \ f_k(x)\geq s(x) \}.$$

Estos son medibles (pues la función $f_k-s$ es medible). Como las $f_k$ son crecientes, claramente $$E_1\subseteq E_2\subseteq E_3\subseteq \dots$$
Más aún, notemos que $$\bigcup_{k=1}^{\infty} E_k =\mathbb{R}^n.$$ Pues dado $x\in \mathbb{R}^n$, si $s(x)=0$, entonces $s(x)\leq f_k(x)$ $\forall k$, de donde $x\in E_k$ para todo $k$. Si $s(x)>0$ $\implies$ $f(x)>0$ $\implies$ $f(x)>s(x)$. Como $f_k(x)\uparrow f(x)$, existe algún $N$ tal que $f_N(x)>s(x)$ $\implies$ $x\in E_N$.

En particular, para cualquier $A\subseteq \mathbb{R}^n$ medible, se tiene $(A\cap E_1)\subseteq (A\cap E_2)\subseteq \dots$ y $A=\bigcup_{k=1}^{\infty}(A\cap E_k)$. Luego, por monotonía de la medida de Lebesgue: \begin{equation} \lambda(A)=\lim_{k\to \infty} \lambda(A\cap E_k). \end{equation}

Ahora, usando que $\chi_{A\cap B}=\chi_A\chi_B$, tenemos: $$f_k\geq f_k\chi_{E_k}\geq s_k\chi_{E_k}= \sum_{j=1}^{m}\alpha_j\chi_{A_j\cap E_k}$$ \begin{equation} \implies \int f_k \ \mathrm{d}\lambda\geq \sum_{j=1}^{m}\alpha_j\lambda (A_j\cap E_k). \end{equation} Haciendo tender $k\longrightarrow \infty$ en (2) y usando (1), concluimos finalmente: $$\lim_{k\to \infty} \int f_k \ \mathrm{d}\lambda\geq \lim_{k\to \infty} \left( \sum_{j=1}^{m}\alpha_j\lambda (A_j\cap E_k) \right)=\sum_{j=1}^{m}\alpha_j\lambda (A_j)=\int s \ \mathrm{d}\lambda>c.$$ Lo que completa la demostración.

$\square$

Corolario. Si $f,g:\mathbb{R}^n\to [0,\infty]$ son funciones medibles no negativas, entonces: $$\int (f+g) \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda+\int g \ \mathrm{d}\lambda.$$

Demostración. Como ya sabemos, podemos encontrar sucesiones crecientes en $S$ , digamos $\{ s_k \}_{k=1}^{\infty}$ y $\{ t_k \}_{k=1}^{\infty}$, tales que $$s_k\uparrow f \ \ \text{y} \ \ t_k\uparrow g.$$ De donde claramente $$(s_k+t_k)\uparrow f+g.$$
Por el teorema de la convergencia monótona, aplicado a las sucesiones $\{ s_k \}_{k=1}^{\infty}$, $\{ t_k \}_{k=1}^{\infty}$, $\{ s_k+t_k\}_{k=1}^{\infty}$ podemos concluir:

\begin{align*}
\int (f+g) \ \mathrm{d}\lambda &= \lim_{k\to \infty} \int (s_k+t_k) \ \mathrm{d}\lambda\\
&= \lim_{k\to \infty} \left( \int s_k \ \mathrm{d}\lambda+\int t_k \ \mathrm{d}\lambda \right) \\
&= \lim_{k\to \infty} \left( \int s_k \ \mathrm{d}\lambda \right)+ \lim_{k\to \infty} \left( \int t_k \ \mathrm{d}\lambda \right) \\
&= \int f \ \mathrm{d}\lambda+\int g \ \mathrm{d}\lambda.
\end{align*}

Pues ya sabemos que $\int (s+t) \ \mathrm{d}\lambda=\int s \ \mathrm{d}\lambda+\int t \ \mathrm{d}\lambda$ si $s,t\in S$.

$\square$

Corolario. Si $f_1,f_2,f_3\dots$ es una sucesión de funciones medibles no negativas en $\mathbb{R}^n$, entonces $$\int \sum_{k=1}^{\infty} f_k \ \mathrm{d}\lambda= \sum_{k=1}^{\infty}\int f_k \ \mathrm{d}\lambda.$$

Demostración. Como las $f_k$ son no negativas, la sucesión de sumas parciales $$P_N=\sum_{k=1}^{N}f_k.$$ Es una sucesión creciente de funciones medibles no negativas. Así que su límite $$\sum_{k=1}^{\infty}f_k.$$ Existe y es una función medible (en cada punto es el límite de una sucesión creciente de números extendidos).

Como $f_k\geq 0$ $\implies$ $\int f_k \ \mathrm{d}\lambda\geq 0$ para toda $k$, de modo que la sucesión de sumas parciales de integrales $\sum_{k=1}^{N} \int f_k \ \mathrm{d}\lambda$ es creciente y por lo tanto tiene un límite (posiblemente extendido): $$\sum_{k=1}^{\infty} \int f_k \ \mathrm{d}\lambda.$$

Por el teorema de la convergencia monótona aplicado a $\{ P_N\}_{N=1}^{\infty}$ y el primer corolario:

\begin{align*}
\int \sum_{k=1}^{\infty} f_k \ \mathrm{d}\lambda &=\int \left( \lim_{N\to \infty} \sum_{k=1}^{N} f_k \right) \ \mathrm{d}\lambda \\
&= \lim_{N\to \infty} \int \sum_{k=1}^{N} f_k \ \mathrm{d}\lambda \\
&= \lim_{N\to \infty} \sum_{k=1}^{N} \int f_k \ \mathrm{d}\lambda \\
&= \sum_{k=1}^{\infty} \int f_k \ \mathrm{d}\lambda.
\end{align*}

$\square$

Más adelante…

Veremos que, en general, las hipótesis del teorema de la convergencia monótona no se pueden «relajar mucho». Sin embargo, siempre podemos dar un estimado muy poderoso con respecto a límites e integrales: El Lema de Fatou.

Tarea moral

En los siguientes ejercicios $f,g:\mathbb{R}^n\to [0,\infty]$ denotan funciones medibles no negativas.

• Demuestra que si $\int f \ \mathrm{d}\lambda, \int g \ \mathrm{d}\lambda<\infty$ y $a,b\in \mathbb{R}$ son reales no negativos, entonces $$\int(af+bg) \ \mathrm{d}\lambda=a\int f \ \mathrm{d}\lambda + b\int g \ \mathrm{d}\lambda<\infty.$$
• Sea $r=\sum_{k=1}^{\infty}\alpha_k\chi_{A_k}$, donde para cada $k$, $0\leq \alpha_k<\infty$ y los conjuntos $A_k$ son medibles y ajenos. Demuestra que $$\int r \ \mathrm{d}\lambda=\sum_{k=1}^{\infty}\alpha_k\lambda(A_k).$$
• Aproximando mediante funciones simples y usando el teorema de la convergencia dominada, calcula $$\int_0^1 x \ \mathrm{d}x:=\int_{\mathbb{R}}\chi_{[0,1]}(x)\cdot x \ \mathrm{d}x.$$ [SUGERENCIA: Puede ser útil imitar el primer ejercicio de la entrada Conjuntos medibles – Parte III].
• Para cada $k\in \mathbb{N}$, definamos $f_k(x)=\min(f(x),k)$. Prueba que $$\lim_{k\to \infty}\int f_k \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$
• Para cada $k\in \mathbb{N}$, definamos $t_k=\chi_{[k,k+1]}:\mathbb{R}\to[0,\infty]$.
  • Prueba que la sucesión $\{ t_k\}_{k=1}^{\infty}$ converge puntualmente a 0.
  • Verifica que $$\lim_{k\to \infty}\int t_k \ \mathrm{d}\lambda=1\neq 0 =\int\left( \lim_{k\to \infty}t_k\right) \ \mathrm{d}\lambda.$$
  • ¿Porqué no se puede aplicar el teorema de la convergencia monótona sobre la sucesión $\{t_k \}_{k=1}^{\infty}$?

Introducción

En la entrada pasada definimos el concepto de función simple y como es que estas funciones se integran respecto a la medida de Lebesgue. En esta entrada definiremos la integral para funciones medibles más generales y veremos algunas de sus propiedades.

Integración de funciones no negativas

A modo de recordatorio, en la entrada pasada vimos un resultado interesante: toda función medible no negativa se puede «aproximar» por una sucesión creciente de funciones simples. Es entonces natural definir la integral de una función medible y no negativa precisamente como una aproximación de integrales de funciones simples, que ya sabemos como «integrar».

Al igual que en la entrada pasada, denotaremos por $S$ al conjunto de funciones simples medibles $s$ con $0\leq s\leq \infty$.

Definición. Supongamos que $f:\mathbb{R}^n\to [0,\infty]$ es una función medible no negativa. Definimos la integral de $f$ respecto a la medida de Lebesgue como: $$\int f \ \mathrm{d}\lambda=\sup\left\{ \int s \ \mathrm{d}\lambda \ | \ s\leq f, \ s\in S \right\}.$$

Observa que la integral está bien definida para cualquier función medible no negativa al ser el supremo de un conjunto.

Otras notaciones que usaremos a menudo para denotar la integral (y que puedes encontrar en la bibliografía) son $$\int f, \ \
\int_{\mathbb{R}^n} f, \ \ \int_{\mathbb{R}^n} f \ \mathrm{d}\lambda, \ \ \int f \ \mathrm{d}x, \ \ \int_{\mathbb{R}^n} f(x) \ \mathrm{d}x.$$

Entre otras. En algunos textos, también se puede denotar como:
$$\int_{\mathbb{R}^n} \mathrm{d}\lambda \ f, \ \ \int_{\mathbb{R}^n} \mathrm{d}x \ f(x) .$$

Proposición (Propiedades de la integral de una función no negativa).

1. $0\leq \int f \ \mathrm{d}\lambda \leq \infty$
2. Si $0\leq c<\infty$ es una constante, $\int cf \ \mathrm{d}\lambda=c\int f \ \mathrm{d}\lambda.$
3. Si $f\leq g$, entonces $\int f \ \mathrm{d}\lambda\leq \int g \ \mathrm{d}\lambda.$
4. Si $\int f \ \mathrm{d} \lambda=0$ $\implies$ $Z=\{ x \ | \ f(x)>0 \}$ es un conjunto nulo.

Demostración. 1 es inmediato pues $\int f \ \mathrm{d}\lambda$ es el supremo de un conjunto de números $\geq 0$ .

Para 2. notemos simplemente que:

\begin{align*}
\int cf \ \mathrm{d}\lambda &= \sup\left\{ \int s \ \mathrm{d}\lambda \ | \ s\leq cf, \ s\in S \right\} \\
&=\sup\left\{ \int ct \ \mathrm{d}\lambda \ | \ t\leq f, \ t\in S \right\} \\
&=\sup\left\{ c\int t \ \mathrm{d}\lambda \ | \ t\leq f, \ t\in S \right\} \\
&=c \ \sup\left\{ \int t \ \mathrm{d}\lambda \ | \ t\leq f, \ t\in S \right\} \\
&= c \int f \ \mathrm{d}\lambda.
\end{align*}

Si $f\leq g$, claramente

$$\left\{ \int s \ \mathrm{d}\lambda \ | \ s\leq f, \ s\in S \right\}\subseteq \left\{ \int t \ \mathrm{d}\lambda \ | \ t\leq g, \ t\in S \right\}$$

Tomando supremos se sigue 3.

Para 4. procedamos por contradicción: Supongamos que $\lambda(Z)>0$. Para cada $k$, definamos $Z_k=\{ x \ | \ f(x)>\frac{1}{k} \}$. Entonces $Z_1\subseteq Z_2\subseteq Z_3\subseteq\dots$ es una sucesión creciente de conjuntos medibles con $$Z=\bigcup_{k=1}^{\infty} Z_k.$$ Así que por monotonía de la medida de Lebesgue: $$\lambda(Z_k)\uparrow \lambda(Z).$$ En particular, podemos encontrar un $N$ suficientemente grande tal que $\lambda(Z_N)>0$. Consideremos ahora la función $s=\frac{1}{N}\chi_{Z_N}\in S$. Notemos que $s\leq f$. Entonces por definición: $$0<\frac{1}{N}\lambda(Z_N)=\int s \ \mathrm{d} \lambda\leq \int f \ \mathrm{d} \lambda$$ Lo cual es una contradicción.

$\square$

Por analogía al caso para integrales simples, uno podría esperar que $$\int (f+g) \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda+\int g \ \mathrm{d}\lambda.$$ Esto es de hecho cierto pero no es trivial. Por un análisis similar a los anteriores es sencillo probar que $\int (f+g) \ \mathrm{d}\lambda \geq \int f \ \mathrm{d}\lambda+\int g \ \mathrm{d}\lambda$, sin embargo, es fácil convencerse de que la desigualdad opuesta requiere mucho más trabajo.

Para afrontar dificultades como la anterior, introduciremos uno de los teoremas más fundamentales de la teoría de integración de Lebesgue: El teorema de La convergencia monótona.

Más adelante…

Enunciaremos y probaremos el Teorema de la Convergencia Monótona, una de las herramientas más importantes en la teoría de integración y veremos algunas de sus consecuencias. Como un corolario muy importante, veremos que simplifica considerablemente la demostración de que $\int (f+g) \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda+\int g \ \mathrm{d}\lambda$.

Tarea moral

En los siguientes ejercicios, $f,g:\mathbb{R}^n\to [0,\infty]$ denotan funciones medibles no negativas.

• Demuestra que $\int (f+g) \ \mathrm{d}\lambda\geq \int f \ \mathrm{d}\lambda + \int g \ \mathrm{d}\lambda$.
• (Propiedad de finitud). Demuestra que si $\int f \ \mathrm{d}\lambda<\infty$, entonces $$\lambda(\{x \ | \ f(x)=\infty \})=0.$$
• Verifica que el punto 2. de la proposición es válido aún cuando $c=+\infty$, es decir $$\int \infty\cdot f \ \mathrm{d}\lambda=\infty \cdot \int f \ \mathrm{d}\lambda.$$ (En este ejercicio suponemos la convención $0\cdot \infty=0$).
• Demuestra que si $\lambda(\{x \ | \ f(x)=\infty \})>0$, entonces $$\int f \ \mathrm{d}\lambda = \infty.$$[SUGERENCIA: Usando la monotonía de la medida de Lebesgue, prueba que existe $N>0$ suficientemente grande tal que $\lambda(\{x \ | \ f(x)=N \})>0$].
• (Desigualdad de Chebyshev). Demuestra que si $\int f \ \mathrm{d}\lambda<\infty$, entonces $$\lambda(\{x \ | \ f(x)\geq \alpha \})\leq \frac{1}{\alpha}\int f \ \mathrm{d}\lambda.$$ [SUGERENCIA: Sea $A=\{x \ | \ f(x)\geq \alpha \}$. Usa monotonía sobre $\alpha \chi_A \leq f$].

Introducción

En las entradas anteriores construimos la maquinaria teórica sobre la que podemos definir un nuevo concepto de integral: «La integral de Lebesgue». En esta entrada estudiaremos las funciones simples y cómo es que se pueden integrar.

Las funciones simples son simplemente aquellas que toman una cantidad finita de valores. Resultan ser «las funciones más sencillas que se pueden integrar».

Funciones simples

En esta sección, $X$ denota un conjunto arbitrario y $\mathcal{M}$ una $\sigma$-álgebra sobre $X$.

Definición. Decimos que $s:X\to [-\infty,\infty]$ es una función simple si toma solamente una cantidad finita de valores.

Si $s$ es simple, podemos escribir: $$s=\sum_{k=1}^{m}\alpha_k \chi_{A_k},$$ Donde $\alpha_1,\dots, \alpha_m$ son los distintos valores del rango de $s$ y $A_k=\{ x\in X \ | \ f(x)=\alpha_k \}=f^{-1}(A_k)$ son conjuntos ajenos. (Como es usual $\chi_A$ denota la función característica del conjunto $A$, i.e. $\chi_A(x)=1$ si $x\in A$ y $\chi_A(x)=0$ en otro caso).

Observación. Hay muchas formas de escribir una función simple como combinación lineal de funciones características. La anterior es sólo una de ellas. A estas expresiones las llamaremos representaciones.

Las funciones simples y medibles admiten representaciones muy particulares como muestra la siguiente proposición. La demostración es una consecuencia sencilla de las propiedades de las funciones medibles y se deja como tarea moral.

Proposición. Si $\mathcal{M}$ es una $\sigma$-álgebra sobre $X$, una función simple $s$ es $\mathcal{M}$-medible si y sólo si admite una representación $s=\sum_{k=1}^{m}\alpha_k \chi_{A_k}$, con $A_k\in \mathcal{M}$ para todo $k$.

$\square$

Antes de definir de lleno la integral de una función simple, veremos una proposición muy útil que, en general, nos dice que podemos aproximar cualquier función medible con funciones simples.

Teorema (de aproximación por funciones simples). Supongamos que $f:X\to [-\infty, \infty]$ es $\mathcal{M}$-medible. Entonces existe una sucesión $s_1,s_2,\dots$ de funciones simples $\mathcal{M}$-medibles tales que $$\lim_{k\to \infty} s_k = f.$$ Si $f\geq 0$, podemos tomar la sucesión de modo que $0\leq s_1\leq s_2\ \leq \dots$. O más generalmente si $f$ es $\mathcal{M}$-medible, podemos tomar la sucesión de modo que $|s_1|\leq \ |s_2|\leq \dots$ . Si $f$ es acotada, podemos hacer que la convergencia sea uniforme.

Demostración. Supongamos primero que $f\geq 0$. La idea es sencilla: truncamos la función, cada vez más «finamente», cuidando que eventualmente podamos aproximar cualquier valor (por grande que sea) en el rango de $f$.

Para cada $k\in \mathbb{N}$, definamos la función simple:

\begin{equation*}
s_k(x)=
\begin{cases}
\frac{i-1}{2^k} & \text{si } \frac{i-1}{2^k}\leq f(x) < \frac{i}{2^k}; \ \ i=1,2,\dots,2^k k \\
k & \text{si } k \leq f(x).
\end{cases}
\end{equation*}

Como $f$ es $\mathcal{M}$-medible, los conjuntos $f^{-1}\left( [\frac{i-1}{2^k}, \frac{i}{2^k})\right)$ y $f^{-1}\left( [k,\infty] \right)$ son elementos de $\mathcal{M}$, de donde $s_k$ es $\mathcal{M}$-medible.

Sea $x\in X$. Por un sencillo trabajo por casos, es fácil ver que $s_k(x)\leq s_{k+1}(x)$ para todo $k$ (si $f(x)\in [\frac{2i-2}{2^{k+1}}, \frac{2i-1}{2^{k+1}}) \subseteq [\frac{i-1}{2^k}, \frac{i}{2^k})$, $s_k(x)=s_{k+1}(x)$. En cualquier otro caso $s_k(x)<s_{k+1}(x)$).

Si $f(x)<\infty$, existe algún entero $N$ tal que $f(x)< N$. Luego, si $k\geq N$, por definición \begin{equation} f(x)\in \left[s_k(x), s_k(x)+\frac{1}{2^k}\right) \ \ \implies \ \ |f(x)-s_k(x)|<\frac{1}{2^k}. \end{equation} De donde $s_k(x)\longrightarrow f(x)$ cuando $k\longrightarrow \infty$. Si $f(x)=\infty$, $s_k(x)=k\longrightarrow \infty$ cuando $k\longrightarrow \infty$.

En todo caso, para cualquier $x\in X$ concluimos que $$\lim_{k\to \infty} s_k(x) = f(x).$$

Entonces $s_k$ es la sucesión buscada en este caso.

Veamos ahora el caso general. Notemos que $f=f_+-f_-$. Tomemos sucesiones de funciones simples $0\leq r_1\leq r_2\leq \dots$ y $0\leq t_1 \leq t_2\leq \dots$ que convergen puntualmente a $f_+$ y $f_-$ respectivamente definidas como en el caso anterior. Luego, para cada $k\in \mathbb{N}$, sea $$s_k=r_k-t_k.$$ Claramente es una sucesión de funciones simples tal que $s_k=r_k-t_k\longrightarrow f_+-f_-=f$ puntualmente cuando $k\longrightarrow \infty$.

Dado $x\in X$, si $f(x)\geq 0$, entonces, por construcción, $t_k(x)=0$ $\forall k$ $\implies$ $0\leq r_k(x)=s_k(x)$ $\forall k$. Se sigue que la sucesión $|s_k(x)|=r_k(x)$ es creciente. Similarmente, si $f(x)<0$ se ve que $|s_k(x)|=t_k(x)$ es una sucesión creciente.

Por lo anterior concluimos que $$|s_1|\leq |s_2|\leq |s_3| \leq \dots $$

Si $f$ es acotada, para $N>\sup |f|$ suficientemente grande, tenemos por (1) que para cualquier $x\in X$: $$|f(x)-s_k(x)|\leq |f_+(x)-r_k(x)|+|f_-(x)-t_k(x)|<\frac{1}{2^k}+\frac{1}{2^k}=\frac{1}{2^{k-1}}.$$ Se sigue que en este caso la convergencia es uniforme.

$\square$

Veamos una aplicación del resultado anterior. Como probamos anteriormente, los conjuntos Lebesgue medibles son «casi» Borel medibles. Es entonces esperable que las funciones Lebesgue medibles sean «casi» funciones Borel medibles.

Ejemplo. Sea $f:\mathbb{R}^n\to [-\infty,\infty]$ una función Lebesgue-medible. Entonces existe una función $g:\mathbb{R}^n\to[-\infty,\infty]$ Borel-medible tal que el conjunto $$\{ x\in \mathbb{R}^n \ | \ f(x)\neq g(x) \}.$$ Es nulo.

Demostración. Supongamos primero que $f\geq 0$. Por el teorema anterior, existe una sucesión $$0\leq s_1\leq s_2\leq \dots$$ De funciones simples $\mathcal{L}$-medibles tales que $$\lim_{k\to \infty} s_k=f.$$

Podemos escribir $$s_k=\sum_{j=1}^{m}\alpha_j^k\chi_{A_j^k}. $$
Donde los $\alpha_j^k\in [0,\infty]$ son distintos dos a dos y los conjuntos $A_j^k$ son ajenos y medibles.

Como probamos anteriormente, para cualesquiera $j,k$ admisibles, podemos descomponer $$A_j^k=E_j^k\cup N_j^k$$ Donde $E_j^k\in \mathcal{B}$ y $N_J^K$ es nulo.

Definamos entonces $$\sigma_k=\sum_{j=1}^{m}\alpha_j^k\chi_{E_j^k} $$ Observemos que $\sigma_k$ es una función simple y $\mathcal{B}$-medible para todo $k$. Además, claramente $0\leq \sigma_k\leq s_k$ y $\sigma_k=s_k$ salvo en un conjunto de medida cero $N_k$ (a saber, $N_k=\bigcup_{j=1}^{m}N_j^k$).

Ahora, sean $$N=\bigcup_{k=1}^{\infty}N_k.$$ $$g=\sup_k \sigma_k$$ Notemos que $N$ es nulo. Como $0\leq \sigma_k\leq s_k \leq f$, tomando supremos se tiene $$0\leq g \leq f.$$ Más aún, para cualquier $x\notin N$, se cumple $\sigma_k(x)=s_k(x)$ $\forall k$ $\implies$ $$g(x)=\sup_k \sigma_k(x)=\lim_{k\to \infty} s_k(x)=f(x).$$ Por lo que $f=g$ salvo un conjunto de medida cero ($N$). $g$ es $\mathcal{B}$-medible al ser el supremo de una sucesión de funciones $\mathcal{B}$-medibles. Entonces $g$ es la función buscada.

Consideremos ahora el caso general. Podemos escribir $f=f_+-f_-$. Por lo anterior, existen funciones $\mathcal{B}$-medibles $g_+,g_-$ tales que $0\leq g_+\leq f_+$, $0\leq g_-\leq f_-$ y $f_+=g_+$, $f_-=g_-$ salvo en conjuntos de medida cero. Luego $g=g_+-g_-$ es la función buscada. ($g$ no se «indetermina», pues en los puntos donde $g_+(x)=\infty$, necesariamente $0\leq g_-(x)\leq f_-(x)=0$).

$\square$

Un comentario sobre la generalidad

En la siguiente sección comenzaremos de lleno con teoría de integración sobre $\mathbb{R}^n$. Como lo habíamos adelantado, las funciones $\mathcal{L}$-medibles son las funciones con «la suficiente estructura para ser integradas».

Además de destacar la estructura de la medida de Lebesgue, la razón de que estudiaramos $\sigma$-álgebras y funciones medibles con toda generalidad es que la teoría de integración se puede extender a espacios abstractos de manera inmediata. Como veremos más adelante, basta que exista una función $\mu:\mathcal{M}\to [0,\infty]$ que cumpla propiedades análogas a las de la medida de Lebesgue (una medida general) para poder definir la integral.

Por simplicidad, nos restringiremos al caso más importante e intuitivo: La integración de funciones $\mathcal{L}$-medibles sobre $\mathbb{R}^n$. La construcción de la integral general es idéntica. Basta reemplazar $(\mathbb{R}^n,\mathcal{L},\lambda)$ por $(X,\mathcal{M},\mu)$ respectivamente en cada una de las definiciones y demostraciones debajo.

Integración de funciones simples en $\mathbb{R}^n$

Ya estamos listos para definir la integral de una función simple (y finita) sobre $\mathbb{R}^n$. A manera de motivación, pensemos que $s=\alpha \chi_A$ ($\alpha>0$) es una función (muy) simple en alguna dimensión baja, por ejemplo $\mathbb{R}^2$. Entonces, ¿Cuál es el valor apropiado del «volumen bajo la gráfica» de $s$?. Geométricamente, la región «bajo la gráfica» es un cilindro generalizado con base $A$ y altura $\alpha$ como se observa en la figura. Por analogía con el cálculo de volúmenes de figuras sencillas (o incluso, por analogía con la integral de Riemann), lo más natural es pensar que dicho volúmen debe ser el «área de la base» multiplicado por la «altura». En este caso, por supuesto, podemos interpretar el área de la base como la medida de Lebesgue de $A$, de modo que $$\int s=\alpha\lambda(A).$$
Es la elección más natural para la integral. Similarmente si $s=\sum_{k=1}^{m}\alpha_k\lambda(A_k)$ (con $\alpha_j$ distintos y $A_k$ ajenos), invocando linealidad (o simplemente, «sumando el volúmen de los cilindros por separado») $$\int s=\sum_{k=1}^{m}\alpha_k\lambda(A_k).$$ Es la elección obvia para el valor de la integral.

Definición. Denotaremos por $S_n$ (o simplemente $S$) al conjunto de funciones simples ($\mathcal{L}$-) medibles $s$ en $\mathbb{R}^n$ tales que $0\leq s<\infty$.
Dada $s\in S$, podemos expresarla como $$s=\sum_{k=1}^{m}\alpha_k \chi_{A_k},$$ Donde $0\leq \alpha_k<\infty$ y los conjuntos $A_k$ son medibles y ajenos. Entonces, definimos su integral (respecto a la medida de Lebesgue) como: $$\int s \ \mathrm{d}\lambda := \sum_{k=1}^{\infty}\alpha_k\lambda(A_k). $$

Nota. En esta definición, usamos la convención $0\cdot \infty = 0$.

A priori, el valor de la integral podría depender de la representación de $s$ que tomemos (en la definición no pedimos que los $\alpha_k$ sean distintos, así que puede haber una infinidad de representaciones distintas). Aunque como veremos más adelante, la integral está bien definida.

Veamos las primeras propiedades.

Proposición (Propiedades de la integral de una función simple).

1. $\int s \ \mathrm{d}\lambda$ está bien definida.
2. $0\leq \int s \ \mathrm{d}\lambda \leq \infty.$
3. Si $0\leq c <\infty$ es una constante, $\int cs \ \mathrm{d}\lambda=c\int s \ \mathrm{d}\lambda.$
4. Si $s,t\in S$, entonces $\int (s+t) \ \mathrm{d}\lambda=\int s \ \mathrm{d}\lambda+\int t \ \mathrm{d}\lambda.$
5. Si $s,t\in S$ y $s\leq t$, entonces $\int s \ \mathrm{d}\lambda\leq \int t \ \mathrm{d}\lambda.$

Demostración. Asumiendo 1., los incisos 2. y 3. son inmediatos de la definición.

Probaremos 1. y 5. en el mismo argumento. Supongamos que $s,t\in S$ y $s\leq t$. Tomemos representaciones de $s$ y $t$ de la forma:

\begin{align*}
s &= \sum_{k=1}^{m}\alpha_k\chi_{A_k}, \\
t &= \sum_{j=1}^{l}\beta_j\chi_{B_k}
\end{align*}

Con los $A_k$ y $B_k$ medibles y ajenos dos a dos. Podemos asumir que $\bigcup_{k=1}^{m}A_k=\mathbb{R}^n$ (de no ser así, podemos añadir el término $0\cdot \chi_{A’}$ a la expresión de $s$, donde $A’=\left( \bigcup_{k=1}^{m}A_k \right)^c$, lo que no afecta el valor de la integral bajo esta representación). Similarmente supongamos que $\bigcup_{j=1}^{l}B_j=\mathbb{R}^n$.

Luego, por la aditividad de la medida de Lebesgue y la definición:

\begin{align}
\int s \ \mathrm{d}\lambda &= \sum_{k=1}^{m}\alpha_k\lambda(A_k)=\sum_{k=1}^{m}\sum_{j=1}^{l}\alpha_k\lambda(A_k\cap B_j) \\
\int t \ \mathrm{d}\lambda &= \sum_{j=1}^{l}\beta_j\lambda(B_j)=\sum_{j=1}^{l}\sum_{k=1}^{m}\beta_j\lambda(A_k\cap B_j)
\end{align}

Si $\lambda(A_k\cap B_j)>0$, en particular $A_k\cap B_j\neq 0$, así que podemos tomar un $p\in A_k\cap B_j$. Pero como $s\leq t$: $$\alpha_k=s(p)\leq t(p)=\beta_j.$$
De donde $$\alpha_k\lambda(A_k\cap B_j)\leq \beta_j\lambda(A_k\cap B_j).$$
Si $\lambda(A_k\cap B_j)=0$, es inmediato que $\alpha_k\lambda(A_k\cap B_j)\leq \beta_j\lambda(A_k\cap B_j)$. Comparando (2) y (3) término a término conluimos que: $$\int s \ \mathrm{d}\lambda\leq \int t \ \mathrm{d}\lambda.$$ (Al tomar cualesquiera representaciones válidas de $s$ y $t$). Esto demuestra 5. pero también demuestra 1:

Si tomamos dos representaciones distintas de $s$, la desigualdad $s\leq s$ implica desigualdades simétricas sobre las integrales definidas por las distintas representaciones, lo que garantiza su igualdad.

Ahora veamos 4. Usando la misma notación que en el inciso anterior podemos escribir:
$$s+t=\sum_{k=1}^{m} \sum_{j=1}^{l}(\alpha_k+\beta_j)\chi_{A_k\cap B_j}.$$

Luego:

\begin{align*}
\int (s+t) \ \mathrm{d}\lambda &= \sum_{k=1}^{m} \sum_{j=1}^{l}(\alpha_k+\beta_j)\lambda(A_k\cap B_j) \\
&= \sum_{k=1}^{m} \sum_{j=1}^{l} \alpha_k\lambda(A_k\cap B_j) + \sum_{k=1}^{m} \sum_{j=1}^{l} \beta_j\lambda(A_k\cap B_j) \\
&= \int s \ \mathrm{d}\lambda + \int t \ \mathrm{d}\lambda.
\end{align*}

$\square$

Más adelante…

Definiremos la integral de una función medible y no negativa en general, usando fuertemente las ideas de aproximación por funciones simples y las propiedades de la integral de funciones simples.

Tarea moral

• Prueba que si $\mathcal{M}$ es una $\sigma$-álgebra sobre $X$, una función simple $s$ es $\mathcal{M}$-medible si y sólo si admite una representación $s=\sum_{k=1}^{m}\alpha_k \chi_{A_k}$, con $A_k\in \mathcal{M}$ para todo $k$.
• Prueba que una función $f:X\to [-\infty,\infty]$ es $\mathcal{M}$-medible si y sólo si existe una sucesión de funciones simples y $\mathcal{M}$-medibles $\{ s_k\}_{k=1}^{\infty}$ que convergen puntualmente a $f$.
• Sean $A_1,A_2,\dots,A_m \subseteq \mathbb{R}^n$ conjuntos medibles y casi disjuntos (es decir, $\lambda(A_i\cap A_j)=0$ para todo $i\neq j$). Sea $s=\sum_{k=1}^{m}\alpha_k\chi_{A_k}$ ($0\leq \alpha_k<\infty$ para $k=1,\dots,m$). Prueba que $$\int s \ \mathrm{d}\lambda=\sum_{k=1}^{m}\alpha_k\lambda(A_k).$$

Introducción

En esta entrada continuaremos nuestro estudio de las funciones medibles. Empezaremos repasando los conceptos de límite superior e inferior que serán de gran utilidad en nuestros desarrollos. Posteriormente veremos también que las funciones medibles son cerradas bajo una gran cantidad de operaciones aritméticas y de toma de límites.

Límite superior e inferior

Antes de continuar, conviene dar un breve recordatorio sobre los conceptos de límite superior e inferior de una sucesión que nos encontraremos a menudo en las siguientes entradas. A grandes rasgos, el límite inferior es el «menor punto de acumulación» que admite una sucesión; mientras que el límite superior es el «mayor punto de acumulación» que admite una sucesión. De manera precisa:

Definición. El límite inferior de una sucesión de numeros reales extendidos $\{ x_k \}_{k=1}^{\infty}$ se define como:
$$\limsup_{k\to \infty}x_k=\limsup x_k:=\lim_{k\to \infty} (\inf_{m\geq k}x_m)$$

El límite superior se define como:
$$\limsup_{k\to \infty}x_k=\limsup x_k:=\lim_{k\to \infty} (\sup_{m\geq k} x_m)$$

Observación. Ambos límites siempre existen (aunque son posiblemente infinitos) pues son límites de sucesiones monótonas crecientes y decrecientes respectivamente (a saber $\inf_{m\geq k}x_m$ y $\sup_{m\geq k}x_m$). Por esta misma razón podemos escribir: $$\limsup x_k=\inf_{j\geq 1}(\sup_{k\geq j}x_k); \ \ \ \ \ \liminf x_k=\sup_{j\geq 1}(\inf_{k\geq j}x_k).$$

Proposición. $\{ x_n\}_{n=1}^{\infty}$ converge a $x$ si y sólo si $\liminf_{k}x_k=\limsup_k x_k=x$.

Demostración. ($\impliedby$) Si $\liminf x_k=\limsup x_k = x $, entonces, por definición, las sucesiones:
$$y_k:= \inf_{m\geq k} x_m; \ \ \ \ \ z_k:= \sup_{m\geq k} x_m.$$ Convergen a $x$. Sin embargo, tenemos que:
$$y_m\leq x_m\leq z_m \ \ \ \forall m\in \mathbb{N}.$$

De donde $x_m\longrightarrow x$ cuando $m\longrightarrow \infty$. (Observa que este argumento es válido incluso cuando $x=\pm \infty$).

($\implies$) Supongamos que $\lim_{k\to \infty} x_k=x$.

Los casos $x=\pm \infty$ son sencillos. Los detalles se dejan como tarea moral. Así que supongamos que $-\infty<x<\infty$.

Por definición, dado $\varepsilon>0$ existe $N\in \mathbb{N}$ tal que: $$x-\varepsilon<x_m<x+\varepsilon \ \ \ \forall m\geq N$$

Definiendo las sucesiones $\{ y_k\}_{k=1}^{\infty} $ y $\{ z_k\}_{k=1}^{\infty} $ como en el inciso anterior, al tomar ínfimos, la condición anterior implica que:
$$x-\varepsilon\leq y_N$$ Como la sucesión $\{ y_k\}_{k=1}^{\infty} $ es monótona creciente, y por definición $y_m\leq x_m \leq x+\varepsilon$ $\forall m\geq N$, podemos concluir que:
$$x-\varepsilon\leq y_N\leq y_m < x+\varepsilon \ \ \ \forall m\geq N.$$

Como lo anterior se cumple para cualquier $\varepsilon>0$, concluimos que $y_m\longrightarrow x$ cuando $m\longrightarrow \infty$. Por un argumento similar podemos ver que $z_m\longrightarrow x$ cuando $m\longrightarrow \infty$ que es lo mismo que: $\liminf_{k}x_k=\limsup_k x_k=x$.

$\square$

Más propiedades de funciones medibles

Antes de enunciar el resultado principal de esta entrada, conviene establecer algo de notación que estaremos usando a menudo.

Notación. Si tenemos una sucesión de funciones $\{ f_k \}_{k=1}^{\infty}$, denotaremos a su límite puntual (si existe) como $\lim f_k=\lim_{k\to \infty }f_k$, que recordemos, tiene como regla $(\lim f_k) (x)=\lim_{k\to \infty} f_k(x)$ (el límite actúa punto a punto). Adoptaremos convenciones similares para $\sup$, $\inf$, $\limsup$, $\liminf$, etc. Cuando no genere mayor problema, para aligerar la notación omitiremos los subíndices $\{ k\to \infty\}$ y similares.

Proposición. Sea $\mathcal{M}$ una $\sigma$-álgebra sobre $X$. Sean $f,g:X\to \mathbb{R}$ funciones $\mathcal{M}$-medibles; $\alpha,\beta\in \mathbb{R}$. Entonces:

1. Si $\phi:\mathbb{R}\to \mathbb{R}$ es Borel-medible, entonces $\phi\circ f$ es $\mathcal{M}$-medible.
2. Si $f\neq 0$, entonces $\frac{1}{f}$ es $\mathcal{M}$-medible.
3. Dado $0<p<\infty$, entonces $|f|^p$ es $\mathcal{M}$-medible.
4. $f+g$ es $\mathcal{M}$-medible.
5. $\alpha f$ es $\mathcal{M}$-medible.
6. $fg$ es $\mathcal{M}$-medible.
7. Si $f_k:X\to [-\infty,\infty]$ es una sucesión de funciones $\mathcal{M}$-medibles entonces cada una de las siguientes funciones es $\mathcal{M}$-medible. (en el caso de la última, condicionada a que esté bien definida).

\begin{align*}
\sup_k f_k&, \ &\inf_k f_k, \\
\limsup_{k\to \infty} f_k&, \ &\liminf_{k\to \infty} f_k, \\
\lim_{k\to \infty} f_k&
\end{align*}

Demostración.

1. Si $E\subseteq{R}$ es de Borel, entonces $\phi^{-1}(E)$ es de Borel ($\phi$ es Borel-medible), luego $(\phi \circ f)^{-1}(E)=f^{-1}(\phi^{-1}(E))\in \mathcal{M}$ ($f$ es $\mathcal{M}$-medible).
2. Definamos
   \begin{equation*}
   h(x)=
   \begin{cases}
   \frac{1}{x} & \text{si } x\neq 0 \\
   0 & \text{si } x =0
   \end{cases}
   \end{equation*}
   Es fácil verificar directamente que $h$ es Borel-medible. Como $f\neq 0$, $h\circ f=\frac{1}{f}$. Del inciso 1 se sigue que $\frac{1}{f}=h\circ f$ es $\mathcal{M}$-medible.
3. Como la función $P(x)=|x|^p$ es continua, en automático es Borel-medible. Luego, por el inciso 1, $|f|^p=P\circ f$ es $\mathcal{M}$-medible.
4. Notemos que $f(x)+g(x)<t$ $\iff$ $f(x)<t-g(x)$ $\iff$ existe $r\in \mathbb{Q}$ tal que $f(x)<r<t-g(x)$. Luego, $$\{ x \ | \ f(x)+g(x)<t \}=\bigcup_{r\in \mathbb{Q}}f^{-1}((-\infty,r))\cap g^{-1}((-\infty,t-r)).$$ Como $f,g$ son $\mathcal{M}$-medibles y $\mathcal{M}$ es $\sigma$-álgebra, se sigue que dicho conjunto pertenece a $\mathcal{M}$.
5. La función $h(x)=\alpha x$ es continua y por tanto Borel-medible. Luego, por el inciso 1, $\alpha f=h\circ f$ es $\mathcal{M}$-medible.
6. Combinando los incisos 3-5 se sigue que la función $$fg=\frac{1}{4}(f+g)^2-\frac{1}{4}(f-g)^2$$ es $\mathcal{M}$-medible.
7. Es fácil ver que $$\{x \ | \ \sup_k f_k(x)\leq t \}=\bigcap_k \{ x\ | \ f_k(x)\leq t \}. $$ Éste último conjunto pertenece a $\mathcal{M}$ (pues las $f_k$ son $\mathcal{M}$-medibles y $\mathcal{M}$ es $\sigma$-álgebra). Se sigue que $\sup f_k$ es $\mathcal{M}$-medible. Similarmente, como $$\{x \ | \ \inf_k f_k(x)\geq t \}=\bigcap_k \{ x\ | \ f_k(x)\geq t \}.$$ Se sigue que $\inf f_k$ es $\mathcal{M}$-medible.
   Por lo anterior, para cada $j\in \mathbb{N}$ la función $\sup_{k\geq j}f_k$ es $\mathcal{M}$-medible, de donde la función $$\limsup f_k =\inf_{j\geq 1}(\sup_{k\geq j} f_k).$$ Es $\mathcal{M}$-medible. Análogamente se ve que $\liminf f_k$ es $\mathcal{M}$-medible.
   Si $\lim f_k(x)$ está definida en cada punto, entonces $$\lim_{k\to \infty}f=\limsup f_k =\liminf f_k.$$ Es $\mathcal{M}$-medible.

$\square$

Como una consecuencia inmediata del último inciso tenemos que:

Corolario. Si $f,g:X\to [-\infty,\infty]$ son funciones $\mathcal{M}$-medibles, entonces $\max (f,g)$ y $\min(f,g)$ son $\mathcal{M}$-medibles.

$\square$

La siguiente definición aparecerá a menudo así que es conveniente recordarla.

Definición. Dado $a\in[-\infty,\infty]$, definimos la parte positiva y negativa de $a$ como:

\begin{equation*}
a_+=
\begin{cases}
a & \text{si } a\geq 0\\
0 & \text{si } a <0
\end{cases} \ \ \ \ ; \\
\ \ \ \ a_-=
\begin{cases}
0 & \text{si } a\geq 0 \\
-a & \text{si } a <0
\end{cases} \\
\end{equation*}

Respectivamente.

Corolario. Si $f:X\to [-\infty,\infty]$ es $\mathcal{M}$-medible, entonces la parte positiva y negativa de $f$, $f_+$ y $f_-$ son también $\mathcal{M}$-medibles.

Demostración. Simplemente notemos que $f_+(x)=\max(f(x),0)$ y $f_-(x)=\max (-f(x),0)$ y apliquemos el corolario anterior.

$\square$

Más adelante

Estudiaremos la definición de función simple: las funciones medibles «más sencillas». Veremos cómo es que aproximan a las demás funciones medibles (lo que a futuro será vital para definir la integral de Lebesgue) y definiremos su integral.

Tarea moral…

• Sea $\{x_k \}_{k=1}^{\infty}$ una sucesión de numeros extendidos. Prueba que existen subsucesiones $\{ x_{k_j}\}_{j=1}^{\infty}$ y $\{ x_{k_l} \}_{l=1}^{\infty}$ que convergen a $\limsup x_k$ y $\liminf x_k$ respectivamente. Demuestra que $\limsup x_k$ y $\liminf x_k$ son el mayor y menor número respectivamente para los que podemos encontrar subsucesiones convergentes.
• Supongamos que para cada $s\in \mathbb{R}$, $f_s:X\to [-\infty,\infty]$ es una función $\mathcal{M}$-medible dada. Supongamos además que para cada $x\in \mathbb{R}$, $\lim_{s\to \infty}f_s(x)=f(x)$ existe. Prueba que $f:X\to [-\infty,\infty]$ es una función $\mathcal{M}$-medible.
• Verifica que la función $f:\mathbb{R}\to\mathbb{R}$ dada por \begin{equation*} f(x)=\begin{cases}
  \frac{1}{x} & \text{ si } x\neq 0 \\
  0 & \text{ si } x=0.
  \end{cases}\end{equation*} Es Borel medible.
• Sea $f:\mathbb{R}\to \mathbb{R}$ una función diferenciable. Demuestra que $f’$ es una función Borel-medible. [SUGERENCIA: $f’$ no necesariamente es continua, pero puede ser vista como límite de funciones continuas].
• Para cada entero positivo $k$, sea $f_k:[0,1]\to [0,\infty]$ una función $\mathcal{L}_{[0,1]}$-medible no negativa. Supongamos que la sucesión $\{f_k\}_{k=1}^{\infty}$ converge puntualmente a $0$. Prueba que para cada $\varepsilon>0$, existe un conjunto medible $E\subseteq [0,1]$ tal que $\lambda(E)<\varepsilon$ y $\{f_k\}_{k=1}^{\infty}$ converge uniformemente a $0$ en $[0,1]\setminus E$. [SUGERENCIA: Prueba que para cada entero positivo $m$, podemos encontrar $N>0$ tal que $\lambda(\{x\in [0,1] \ | \ f_n(x)>\frac{1}{m} \ \ \forall n\geq N \})\leq \frac{\varepsilon}{2^m}$]. Este ejercicio es un caso particular de un resultado más general: el teorema de Egorov.

Introducción

En las siguientes entradas, comenzaremos a desarrollar de lleno la noción de integral de Lebesgue. Es entonces natural pensar en los conjuntos en donde una función $f:\mathbb{R}^n\to \mathbb{R}$ es «aproximadamente constante», es decir, para un $a\in \mathbb{R}$ arbitrario, conjuntos de la forma $$E=\{x\in \mathbb{R}^n \ | \ a\leq f(x)<a+\varepsilon \}.$$

De forma intuitiva, la contribución del conjunto $E$ a la integral debería ser aproximadamente $a\lambda(E)$. Para que esto tenga sentido, es necesaro que el conjunto $E$ sea medible. Si lo anterior se satisface para cualquier $a\in \mathbb{R}$ y $\varepsilon>0$ diremos (provisionalmente) que la función es medible.

Antes de continuar, será muy útil permitir que $f$ tome los valores «extendidos» $\infty$ y $-\infty$. Podemos pensar que $f(x)=\infty$ significa que $f$ «es arbitrariamente grande en $x$» mientras que $f(x)=-\infty$ significa que $f$ es «arbitrariamente negativa en $x$».

La ventaja principal de esta notación es que nos permite trabajar con límites (posiblemente infinitos) de una manera unificada. Por ejemplo, si $\{ f_k \}_{k=1}^{\infty}$ es una sucesión de funciones tales que $\lim_k f_k(x)$ existe para todo $x\neq 0$ y $f_k(0)=k$ para todo $k$, conviene pensar que la sucesión $\{ f_k \}_{k=1}^{\infty}$ converge puntualmente a una función $f$ con $f(0)=\infty$. A la hora de integrar, esto a veces nos permitirá lidiar con singularidades sencillas de sucesiones de funciones.

Para ello, hace falta extender nuestra noción de números reales y su aritmética a $-\infty$ e $\infty$.

Reales extendidos

Definición. Definimos el sistema de numeros reales extendidos: $$[-\infty,\infty]:=\mathbb{R}\cup\{ -\infty \}\cup \{\infty \}.$$

(De manera formal $\infty,-\infty$ son solamente símbolos, pero conviene pensarlos con su significado usual de cantidades arbitrariamente grandes y arbitrariamente negativas respectivamente. La diferencia es que ahora los pensamos como números sobre los que podemos definir operaciones aritméticas explícitas).

Trabajaremos con las siguientes convenciones (todas éstas son naturales y están formuladas para ser compatibles con las nociones clásicas de límites infinitos): Para cualesquiera $x\in \mathbb{R}$, $0<a\leq \infty$, $-\infty\leq b <0$ convenimos:

\begin{align*}
-\infty < x &< \infty, \\
x + \infty &= \infty, \\
\infty + \infty &= \infty, \\
a\cdot \infty &= \infty, \\
b\cdot \infty &= -\infty.
\end{align*}

Y similarmente

\begin{align*}
x – \infty &= -\infty, \\
-\infty – \infty &= -\infty, \\
a\cdot -\infty &= -\infty, \\
b\cdot -\infty &= \infty.
\end{align*}

Las expresiones $0\cdot \pm \infty$ y $\infty – \infty$ permanecen indefinidas (aunque ocasionalmente, conviene definir la primera como cero).

Dado $A$ un subconjunto de números reales extendidos, convenimos:

• $\sup A:=\infty$ si $\infty\in A$.
• $\sup A= -\infty$ si $A={ -\infty }$.
• $\sup A:= \sup (A\setminus { -\infty})$ si $\infty \notin A$ y $A\neq \{ -\infty\}$ (es decir, el supremo usual de un conjunto de números reales, posiblemente $\infty$ si el conjunto es no acotado).

Las convenciones para $\inf A$ son análogas.

Los límites se trabajan de forma idéntica. Dada una sucesión $\{ a_k\}_{k=1}^{\infty}$ de números reales extendidos:

• Decimos que $\lim_{k\to \infty}a_k=a$, $a\in \mathbb{R}$, si $a_k\in \mathbb{R}$ salvo una cantidad finita de $k$ y $\lim_{k\to \infty}a_k=a$ en el sentido usual (omitiendo los valores extendidos de la sucesión).
• Como es usual, decimos que $\lim_{k\to \infty}a_k=\pm \infty$ si $\forall M\in \mathbb{R}$ positivo $\exists N\in \mathbb{N}$ tal que $\pm x_m>M$ $\forall m\geq N$.

Las convenciones para límites de funciones $\lim_{x\to a }f(x)$ son análogas.

Como consecuencia de nuestras convenciones, es inmediato verificar que los límites extendidos heredan las propiedades de sus contrapartes reales, por ejemplo las referentes a sumas y productos de límites.

El siguiente caso es particularmente frecuente. También es una muestra de las ventajas de adoptar la notación de números reales extendidos.

Observación. Toda sucesión monótona (creciente o decreciente) de números extendidos tiene un límite.

Demostración. En efecto, sea $a_1\leq a_2\leq a_3\leq \dots$ una sucesión monótona creciente de números extendidos. Si la sucesión es acotada y no todos los términos son $-\infty$, se reduce al caso real en el que sabemos que la sucesión converge (y de hecho, converge a su supremo). Si $a_k=-\infty $ para todo $k$, claramente $\lim_{k\to \infty} a_k=-\infty$. Si la sucesión no es acotada entonces $\lim_{k\to \infty} a_k=\infty$. El caso decreciente es similar.

$\square$

Ejemplo. Considera la sucesión de funciones $f_k=k\chi_{[-\frac{1}{k},\frac{1}{k}]}$ (donde $\chi_A$ representa la función característica del conjunto $A$: $\chi_A(x)=1$ si $x\in A$ y $\chi_A(x)=0$ en otro caso). Para cualquier $x\neq 0$, eventualmente $f_k(x)=0$, así que $\lim_{k\to \infty} f_k(x)=0$. Como $f_k(0)=k$ para todo $k$, naturalmente $\lim_{k\to \infty} f_k(0)=\infty$. Concluimos que la sucesión converge puntualmente (en el sentido extendido) a la función

\begin{equation*}
f(x)=
\begin{cases}
0 & \text{si } x \neq 0 \\
\infty & \text{si } x=0 \in \mathbb{R}\setminus\mathbb{Q}.
\end{cases}
\end{equation*}

$\triangle$

Funciones medibles

Ya podemos dar una definición bastante general de función medible sobre conjuntos arbitrarios con alguna $\sigma$-álgebra asociada.

Definición. Sea $f:X\to[-\infty,\infty]$ donde $X$ es un conjunto. Dada $\mathcal{M}$ una $\sigma$-álgebra sobre $X$, decimos que $f$ es $\mathcal{M}$-medible si $\forall t\in [-\infty, \infty]$, el conjunto $$\{ x \ | \ f(x)\leq t\}=f^{-1}([-\infty,t])\in \mathcal{M}.$$

Es conveniente pensar en las funciones medibles como aquellas que «tienen la suficiente estructura como para ser integradas». Si bien definimos el concepto de función medible con toda generalidad (que es necesario para desarrollar nociones de integración sobre espacios «muy generales»), casi siempre trabajaremos con los siguientes dos casos:

• Si $X=\mathbb{R}^n$ y $\mathcal{M}=\mathcal{L}$ diremos que la función es Lebesgue-medible o simplemente medible.
• Si $X=\mathbb{R}^n$ y $\mathcal{M}=\mathcal{B}$ diremos que la función es Borel-medible.

Observación. Como $\mathcal{B}\subseteq \mathcal{L}$, toda función Borel-medible es Lebesgue-medible.

Equivalencias

Como veremos a continuación, existen varias definiciones equivalentes de función medible. Nos moveremos entre ellas con frecuencia.

Proposición. Sea $\mathcal{M}$ una $\sigma$-álgebra sobre $X$ y $f:X\to [-\infty,\infty]$. Entonces $f$ es $\mathcal{M}$-medible si y sólo si cualquiera de las siguientes condiciones se satisface:

1. $f^{-1}([-\infty,t])\in \mathcal{M}$ para todo $t\in[-\infty,\infty]$.
2. $f^{-1}([-\infty,t))\in \mathcal{M}$ para todo $t\in(-\infty,\infty]$.
3. $f^{-1}([t,\infty])\in \mathcal{M}$ para todo $t\in[-\infty,\infty]$.
4. $f^{-1}((t,\infty])\in \mathcal{M}$ para todo $t\in[-\infty,\infty)$.
5. $f^{-1}({ \pm \infty } )\in \mathcal{M}$ y $f^{-1}(E)\in \mathcal{M}$ para cualquier conjunto de Borel $E\subseteq\mathbb{R}$.

Demostración. Las equivalencias 1$\iff $4 y 2$\iff $3 son inmediatas al tomar complementos.

Notemos que $f(x)<t$ si y sólo si existe algún número racional $r\in \mathbb{Q}$ tal que $f(x)\leq r <t$, de donde $$f^{-1}([-\infty,t))=\bigcup_{r\in \mathbb{Q},r<t}f^{-1}([-\infty,r]).$$ Por la cerradura bajo uniones numerables en $\mathcal{M}$, se sigue la implicación 1$\implies$2.

Análogamente podemos ver que $$f^{-1}([-\infty,t])=\bigcap_{r\in \mathbb{Q},r>t}f^{-1}([-\infty,r)).$$
Lo que demuestra similarmente que 2$\implies$1. Esto concluye las equivalencias 1 $\iff$ 2 $\iff$ 3 $\iff$ 4.

La implicación 5$\implies$1 es obvia pues $E=[-\infty,t]$ es de Borel para todo $t$.

Veamos entonces que las condiciones 1-4 implican la condición 5.

Al tomar $t=-\infty$ en 1, se sigue que $f^{-1}({ -\infty})\in \mathcal{M}$. Similarmente al tomar Al tomar $t=\infty$ en 3, se sigue que $f^{-1}({ \infty})\in \mathcal{M}$.

Definamos $\mathcal{S}$ como $$\mathcal{S}=\{ E\subseteq \mathbb{R} \ | \ f^{-1}(E)\in \mathcal{M}\}.$$

Es fácil verificar directamente que $\mathcal{S}$ es una $\sigma$-álgebra. Para lo que resta, es suficiente probar que $\mathcal{S}$ contiene a los conjuntos abiertos de $\mathbb{R}$, pues en ese caso se tendría $\mathcal{B}\subseteq \mathcal{S}$ lo que completa la implicación.

Observemos primero que cualquier abierto de $\mathbb{R}$ es unión numerable de intervalos abiertos. En efecto, dado $U\subseteq \mathbb{R}$ abierto y $s\in
U$, podemos encontrar números racionales $p_s,q_s$ tales que $s\in(p_s,q_s)\subseteq U$. Luego $$U=\bigcup_{s\in U}(p_s,q_s).$$ Es unión numerable de intervalos abiertos.

Por lo anterior y la cerradura de $\sigma$-álgebras bajo uniones numerables, es suficiente probar que los intervalos abiertos son elementos de $\mathcal{S}$. Esto es inmediato pues podemos expresar:
$$f^{-1}((a,b))=f^{-1}([-\infty,b)])\cap f^{-1}((a,\infty]).$$
Que resulta un elemento de $\mathcal{M}$ pues $f^{-1}([-\infty,b)])$ y $f^{-1}((a,\infty])$ son elementos de $\mathcal{M}$ por las condiciones 2 y 4.

$\square$

Algunos ejemplos de funciones medibles

Veamos algunos ejemplos clásicos de funciones medibles. En la sección de ejercicios se detallan algunos otros.

Proposición. Toda función continua $f:\mathbb{R}^n\to \mathbb{R}$ es Borel-medible. En particular es Lebesgue-medible.

Demostración. En la entrada pasada probamos que si $f:\mathbb{R}^n\to \mathbb{R}$ es continua y $A\in \mathcal{B}_1$ $\implies$ $f^{-1}(A)\in \mathcal{B}_n$. Por la proposición anterior, esto garantiza que $f$ es Borel-medible.

$\square$

Proposición. Si $f:\mathbb{R}\to [-\infty,\infty]$ es una función monótona (creciente o decreciente), entonces $f$ es Borel-medible.

Demostración. En efecto, si $f$ es monótona, la imágen inversa de cualquier semirrecta $[t,\infty]$ es algún intervalo, posiblemente abierto, cerrado, semiabierto o semicerrado; pero en todo caso un conjunto de Borel.

$\square$

Otro ejemplo muy importante son las funciones características. Éstas son esenciales para definir el concepto de función simple, que a su vez es fundamental para definir la integral de Lebesgue de una función. La demostración es muy sencilla y se queda como tarea moral.

Proposición. Sea $X$ un conjunto y $\mathcal{M}$ una $\sigma$-álgebra sobre $X$. Si $A\in \mathcal{M}$, entonces, la función característica \begin{equation*} \chi_A(x) =
\begin{cases}
1 & \text{ si } x\in A \\
0 & \text{ si } x \notin A
\end{cases}
\end{equation*} Es $\mathcal{M}$-medible.

$\square$

Ejemplo (funciones medibles sobre subconjuntos). Sea $\mathcal{M}$ una $\sigma$-álgebra sobre $X$ y $f:X\to [-\infty,\infty]$ una función $\mathcal{M}$-medible sobre $X$. Es fácil ver que para cualquier $E\in \mathcal{M}$, la restricción de $f$ sobre $E$, $f_{|E}:E\to [-\infty,\infty]$, es una función $\mathcal{M}_E$-medible ($\mathcal{M}_E$ denota la restricción de $\mathcal{M}$ sobre $E$).

$\triangle$

Más adelante…

Veremos más propiedades de las funciones medibles. En particular veremos que la clase de funciones medibles es cerrada bajo una gran cantidad de operaciones aritméticas y tomas de límite.

Tarea moral

• Verifica las propiedades pendientes de los números reales extendidos.
• Sea $X$ un conjunto y $\mathcal{N}$ una $\sigma$-álgebra sobre $X$. Verifica que si $A\in \mathcal{M}$ $\implies$ $\chi_A$ es $\mathcal{M}$-medible. ¿Qué pasa si $A\notin \mathcal{M}$?
• Sea $X$ un conjunto y $\mathcal{M}=\{X,\emptyset \}$. Demuestra que las únicas funciones $\mathcal{M}$-medibles son las funciones constantes.
• Sea $X$ un conjunto y $\mathcal{M}=2^X$. ¿Qué funciones son $\mathcal{M}$-medibles?
• Sea $X$ un conjunto y $\mathcal{M}$ una $\sigma$-álgebra sobre $X$. Sea $A\in \mathcal{M}$ y $f:A\to [-\infty,\infty]$ una función definida sobre $E$. Demuestra que $f$ es $\mathcal{M}_A$-medible $\iff$ $f^{-1}([-\infty,t])\in \mathcal{M}$ para todo $t\in[-\infty, \infty]$ $\iff$ $f^{-1}(\pm \infty)\in \mathcal{M}$ y $f^{-1}(K)\in \mathcal{M}$ para todo $K\subseteq \mathbb{R}$ conjunto de Borel.
• Decimos que una función $f:\mathbb{R}\to \mathbb{R}$ es continua a pedazos, si existen puntos $\dots <x_{-2}<x_{-1}<x_0<x_1<x_2<\dots$ tales que $f$ es continua en $(x_k,x_{k+1})$ para todo $k\in \mathbb{Z}$. Prueba que toda función continua a pedazos es Borel-medible. Prueba también que es Lebesgue-medible.