Introducción
El teorema integral de Cauchy es una de las piedras angulares del análisis complejo. Dicho resultado resuelve dos características aparentemente contradictorias de las integrales de contorno cuando $f$ es una función fija pero el contorno $\gamma$, a lo largo del que se integrará a $f$, puede cambiar. Por una parte, es posible modificar el contorno $\gamma$ de forma bastante drástica sin efecto en la integral, por ejemplo, reemplazando un contorno simple por un contorno no simple a trozos. Por otra parte, si cambiamos un contorno semicircular en el semiplano superior del plano complejo $\mathbb{C}$, que une a $-1$ y $1$, por un contorno semicircular en el semiplano inferior de $\mathbb{C}$, que une a $-1$ y $1$, tenemos que el resultado de la integral de $f(z)=z^{-1}$ a lo largo de dichos contornos cambia completamente. Entonces, a través del teorema integral de Cauchy nos será posible explicar estas dos características y concluir que lo que realmente importa es el número de vueltas que un contorno $\gamma$ da alrededor de los puntos que se encuentran fuera del dominio de $f$.
El teorema integral de Cauchy-Goursat establece que dentro de ciertos dominios la integral de una función analítica a lo largo de un contorno cerrado simple es cero. Una extensión de este teorema nos permitirá reemplazar integrales sobre ciertos contornos complicados con integrales sobre contornos que son fáciles de evaluar.
En esta entrada abordaremos una versión local del teorema integral de Cauchy para discos abiertos, la cual nos permitirá obtener un resultado general de dicho teorema.
Recordemos el siguiente resultado visto en nuestros cursos de Cálculo.
Teorema 36.1. (Teorema de Green.)
Sea $C$ una curva de clase $C^1$, cerrada, simple y orientada positivamente, tal que es la frontera de una región $D\subset\mathbb{R}^2$. Si $P, Q: D\to \mathbb{R}$ son dos funciones reales de clase $C^{1}$, entonces:
\begin{equation*}
\int_{C} P dx + Q dy = \iint_{D} \left(\frac{\partial Q}{\partial x} – \frac{\partial P}{\partial y}\right) dx dy.
\end{equation*}
Procedemos a enunciar una primera versión del teorema integral de Cauchy para rectángulos.
Teorema 36.2. (Primera versión del Teorema Integral de Cauchy.)
Sean $U\subset\mathbb{C}$ un conjunto abierto, $f:U\to\mathbb{C}$ una función de clase $C^1$ y $R\subset U$ un rectángulo cerrado con frontera $\partial R$ orientada positivamente. Entonces:
\begin{equation*}
\int_{\partial R} f(z) dz = 0.
\end{equation*}
Demostración. Dadas las hipótesis, sea $f(z)=u(x,y)+iv(x,y)$.
De la definición 17.2 se tiene que $f$ es de clase $C^1$ si y solo si $u, u: U \to \mathbb{R}$ son dos funciones reales de clase $C^1$. Más aún, por el teorema 17.1 se cumple que las funciones $u$ y $v$ satisfacen las ecuaciones de C-R, por ser $f$ una función analítica en $U$. Entonces, para $dz = dx+idy$, por la observación 34.3 y el Teorema de Green, se tiene que:
\begin{align*}
\int_{\partial R} f(z) dz & = \int_{\partial R} (udx-vdy) + i \int_{\partial R} (vdx+udy)\\
& = \iint_{R} \left(-\frac{\partial v}{\partial x} – \frac{\partial u}{\partial y}\right) dx dy + i\iint_{R} \left(\frac{\partial u}{\partial x} – \frac{\partial v}{\partial y}\right) dx dy\\
& = \iint_{R} \left(\frac{\partial u}{\partial y} – \frac{\partial u}{\partial y}\right) dx dy + i \iint_{R} \left(\frac{\partial u}{\partial x} – \frac{\partial u}{\partial x}\right) dx dy\\
& = 0.
\end{align*}
$\blacksquare$
Bajo la hipótesis adicional de que $f'(z)$ es continua para todo $z\in U$, la demostración de esta primera versión del Teorema de Cauchy es clara. Aunque el Teorema de Green fue establecido hasta 1828, fue Augustin Cauchy quien en 1814 demostró por primera vez el teorema 36.1, bajo la hipótesis adicional de continuidad sobre $f’$, utilizando una formulación equivalente a la establecida en el Teorema de Green.
Observación 36.1.
Más adelante probaremos que las derivadas de una función analítica son también funciones analíticas y por tanto continuas, proposición 16.1, entonces la hipótesis de continuidad sobre $f’$ resulta redundante e innecesaria.
Procedemos ahora a probar una versión local del Teorema integral de Cauchy para discos.
Teorema 36.3. (Teorema Integral de Cauchy-Goursat para discos.)
Sean $r>0$, $z_0\in \mathbb{C}$ un punto fijo y $f:B(z_0, r) \to \mathbb{C}$ una función analítica en el disco abierto $B(z_0, r)$. Entonces:
\begin{equation*}
\int_{\gamma} f(z) dz = 0,
\end{equation*}para cualquier contorno cerrado $\gamma$ en $B(z_0, r)$.
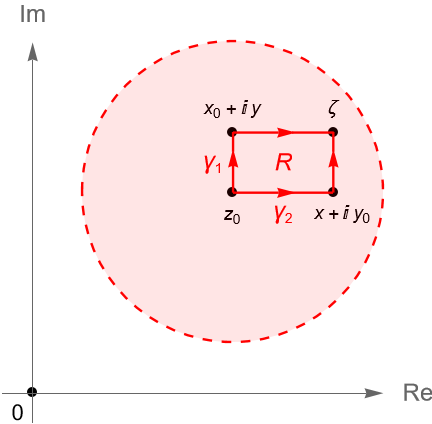
Demostración. Dadas las hipótesis, sea $z_0=x_0+iy_0$ el centro del disco $B(z_0,r)$, $\zeta=x+iy\in B(z_0,r)$ cualquier punto y $f(z)=u(x,y)+iv(x,y)$. De acuerdo con la proposición 35.2 basta con probar que existe una primitiva de $f$ en $B(z_0,r)$.
Sea $\gamma_1$ el contorno dado por el segmento de recta vertical que une a $z_0$ con $x_0+iy$ seguido del segmento de recta horizontal que une a $x_0+iy$ con $\zeta$, es decir, $\gamma_1 := [z_0, x_0+iy]+[x_0+iy, \zeta]$. Análogamente, definimos al contorno $\gamma_2$ dado por el segmento de recta horizontal que une a $z_0$ con $x+iy_0$ seguido del segmento de recta vertical que une a $x+iy_0$ con $\zeta$, es decir, $\gamma_2 := [z_0, x+iy_0]+[x+iy_0, \zeta]$, figura 134.
Es claro que el contorno $\gamma = \gamma_2 + (-\gamma)$ es un contorno cerrado y coincide con la frontera $\partial R$ del rectángulo $R\subset B(z_0,r)$ con vértices $z_0, x+iy_0, \zeta, x_0+iy \in B(z_0,r)$. Por lo que, del lema de Goursat y la proposición 34.2, tenemos que:
\begin{align*}
0 & = \int_{\partial R} f(z) dz\\ & = \int_{z_0}^{x+iy_0} f(z) dz + \int_{x+iy_0}^{\zeta} f(z) dz + \int_{\zeta}^{x_0+iy} f(z) dz + \int_{x_0+iy}^{z_0} f(z) dz\\
& = \int_{\gamma_2} f(z) dz + \int_{-\gamma_1} f(z) dz.
\end{align*}
Es decir:
\begin{equation*}
\int_{\gamma_2} f(z) dz = – \int_{-\gamma_1} f(z) dz = \int_{\gamma_1} f(z) dz.
\end{equation*}
Considerando lo anterior definimos a la función:
\begin{equation*}
F(z) := \int_{\gamma_1} f(z) dz = \int_{\gamma_2} f(z) dz.
\end{equation*}
Veamos que $F$ es una primitiva de $f$ en $B(z_0, r)$.
Como en los segmentos $[z_0, x+iy_0]$ y $[x_0+iy, \zeta]$ el término imaginario es constante, entonces podemos parametrizar a dichos segmentos, respectivamente, como:
\begin{align*}
\beta_1(t) & = t+iy_0, \quad \forall \, t\in [x_0, x],\\
\beta_2(t) & = t+iy, \quad \forall \, t\in [x_0, x].
\end{align*}
Análogamente, en los segmentos $[z_0, x_0+iy]$ y $[x+iy_0, \zeta]$ el término real es constante, por lo que podemos parametrizar a dichos segmentos, respectivamente, como:
\begin{align*}
\beta_3(t) & = x_0+it, \quad \forall \, t\in [y_0, y],\\
\beta_4(t) & = x+it, \quad \forall \, t\in [y_0, y].
\end{align*}
Entonces, de la definición 34.1 y la proposición 33.1, se sigue que:
\begin{align*}
F(z) & = \int_{\gamma_1} f(z) dz\\
& = \int_{\beta_1} f(z) dz + \int_{\beta_4} f(z) dz\\
& = \int_{x_0}^{x} f(t+iy_0) dt + i\int_{y_0}^{y} f(x+it) dt\\
& = \int_{x_0}^{x} u(t+iy_0) dt + i \int_{x_0}^{x} v(t+iy_0) dt – \int_{y_0}^{y} v(x,t) dt + i\int_{y_0}^{y} u(x,t) dt.
\end{align*}
Por el primer Teorema Fundamental del Cálculo tenemos que:
\begin{align*}
\frac{\partial F(z)}{\partial y} & = \frac{\partial}{\partial y} \int_{x_0}^{x} u(t+iy_0) dt + i \frac{\partial}{\partial y} \int_{x_0}^{x} v(t+iy_0) dt\\
& \quad \,\, – \frac{\partial}{\partial y} \int_{y_0}^{y} v(x,t) dt + i \frac{\partial}{\partial y} \int_{x_0}^{x} u(x,t) dt\\
& = 0 + i 0 – v(x,y) + i u(x,y)\\
& = i\left[u(x,y) + i v(x,y)\right]\\
& = i f(z).
\end{align*}
Procediendo de manera análoga tenemos que:
\begin{equation*}
F(z) = \int_{\beta_2} f(z) dz + \int_{\beta_3} f(z) dz,
\end{equation*}de donde:
\begin{equation*}
\frac{\partial F(z)}{\partial x} = f(z).
\end{equation*}
Tenemos que:
\begin{equation*}
0 = f(z) – f(z) = \frac{\partial F(z)}{\partial x} + i \frac{\partial F(z)}{\partial y},
\end{equation*}es decir, si $F(z)=U(x,y) + i V(x,y)$, entonces:
\begin{equation*}
\frac{\partial U}{\partial x} = \frac{\partial V}{\partial y}, \quad \frac{\partial U}{\partial y} = – \frac{\partial V}{\partial x},
\end{equation*}por lo que $U$ y $V$ satisfacen las ecuaciones de C-R. Más aún, como $f$ es analítica en $B(z_0, r)$, en particular es continua, por lo que $U_x, U_y, V_x$ y $V_y$ son continuas, es decir, $F$ es una función de clase $C^1(B(z_0, r))$, entonces por el teorema 18.1 tenemos que $F$ es una función analítica en $B(z_0, r)$ tal que:
\begin{equation*}
F'(z) = \frac{\partial F(z)}{\partial x} = – i \frac{\partial F(z)}{\partial y} = f(z), \quad \forall z\in B(z_0, r),
\end{equation*}es decir, $F$ es una primitiva de $f$ en $B(z_0, r)$, por lo que de la proposición 35.2 se sigue que:
\begin{equation*}
\int_{\gamma} f(z) dz = 0,
\end{equation*}para cualquier contorno cerrado $\gamma$ en $B(z_0, r)$.
$\blacksquare$
Ejemplo 36.1.
Evaluemos la integral:
\begin{equation*}
\int_{\gamma} \frac{e^z}{z^2-16} dz,
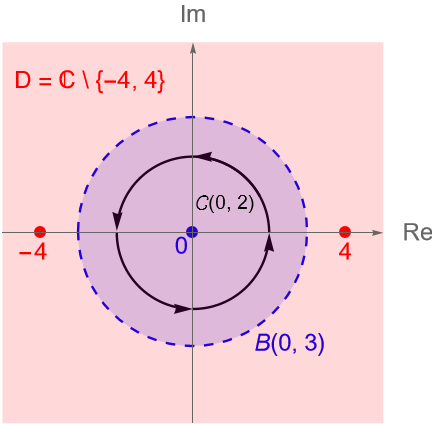
\end{equation*}donde $\gamma$ describe a la circunferencia $C(0,2)$ orientada positivamente y recorrida una vez.
Solución. Es claro que la función:
\begin{equation*}
f(z) = \frac{e^z}{z^2-16},
\end{equation*}es analítica en $D = \mathbb{C}\setminus\{-4, 4\}$ y en particular es analítica en el disco abierto $B(0,3) \subset D$.
Por otra parte, tenemos que el contorno cerrado $C(0,2)$, parametrizado por $\gamma(t)=2e^{it}$, con $t\in[0,2\pi]$, está completamente contenido en el disco $B(0,3)$, figura fig:f135, por lo que del teorema 36.3 se sigue que:
\begin{equation*}
\int_{\gamma} \frac{e^z}{z^2-16} dz =0.
\end{equation*}
Ejemplo 36.2.
Veamos que
\begin{equation*}
\int_{0}^{\infty} \operatorname{cos}(t^2) dt = \int_{0}^{\infty} \operatorname{sen}(t^2) dt = \frac{\sqrt{2\pi}}{4}.
\end{equation*}
Solución. Es claro que ambas integrales son integrales reales impropias, por lo que debemos probar que:
\begin{equation*}
\lim_{r\to \infty}\int_{0}^{r} \operatorname{cos}(t^2) dt = \lim_{r\to \infty} \int_{0}^{r} \operatorname{sen}(t^2) dt = \frac{\sqrt{2\pi}}{4}.
\end{equation*}
Dado que $e^{it^2} = \operatorname{cos}(t^2) + \operatorname{sen}(t^2)$, basta probar que:
\begin{equation*}
\lim_{r\to \infty}\int_{0}^{r} e^{t^2} dt = \frac{(1+i)\sqrt{2\pi}}{4},
\end{equation*}y tomar la parte real e imaginaria para obtener el resultado.
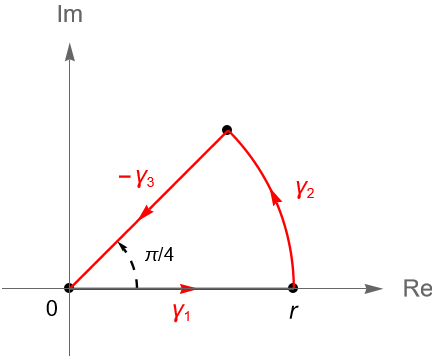
Sea $f(z) = e^{iz^2}$. Definimos al contorno cerrado $\gamma = \gamma_1+\gamma_2-\gamma_3$, firgura 136, donde:
\begin{align*}
\gamma_1(t) & = t, \quad \forall t\in[0,r]\\
\gamma_3(t) & = te^{i\pi/4}, \quad \forall t\in[0,r],\\
\gamma_2(t) & = re^{it}, \quad \forall t\in[0,\pi/4].
\end{align*}
Tenemos que $f$ es una función entera, por lo que es analítica en cualquier disco abierto, en particular si consideramos al disco abierto $B(0,R)$, con $0<r<R$, entonces es claro que el contorno $\gamma$ está completamente contenido en $B(0,R)$, por lo que del Teorema Integral de Cauchy-Goursat, para discos y de la proposición 34.2, se sigue que:
\begin{equation*}
0 = \int_{\gamma} e^{iz^2} dz = \int_{\gamma_1} e^{iz^2} dz + \int_{\gamma_2} e^{iz^2} dz – \int_{\gamma_3} e^{iz^2} dz,
\end{equation*}por lo que:
\begin{align*}
\int_{0}^{r} e^{it^2} dt & = \int_{\gamma_1} e^{iz^2} dz\\
& = \int_{\gamma_3} e^{iz^2} dz – \int_{\gamma_2} e^{iz^2} dz\\
& = \frac{(1+i)\sqrt{2}}{2} \int_{0}^{r} e^{-t^2} dt – \int_{\gamma_2} e^{iz^2} dz. \tag{36.1}
\end{align*}
Por el ejemplo 34.11 sabemos que:
\begin{equation*}
\left|\int_{\gamma_2} e^{iz^2} dz\right| \leq \frac{\pi(1-e^{r^2})}{4r},
\end{equation*}por lo que, tomando el límite cuando $r \to \infty$ tenemos que:
\begin{equation*}
\left|\int_{\gamma_2} e^{iz^2} dz\right| = 0, \quad \Longrightarrow \int_{\gamma_2} e^{iz^2} dz = 0.
\end{equation*}
Entonces, tomando el límite cuando $r \to \infty$ en (36.1) tenemos que:
\begin{equation*}
\lim_{r \to \infty} \int_{0}^{r} e^{it^2} dt = \frac{(1+i)\sqrt{2}}{2} \lim_{r \to \infty} \int_{0}^{r} e^{-t^2} dt.
\end{equation*}
De nuestros cursos de Cálculo sabemos que:
\begin{equation*}
\int_{0}^{\infty} e^{-t^2} dt = \frac{\pi}{2},
\end{equation*}por lo que:
\begin{equation*}
\int_{0}^{\infty} e^{it^2} dt = \lim_{r \to \infty} \int_{0}^{r} e^{it^2} dt = \frac{(1+i)\sqrt{2}}{2} \frac{\pi}{2} = \frac{(1+i)\sqrt{2\pi}}{4}.
\end{equation*}
Por último, tomando la parte real e imaginaria de esta última igualdad tenemos el resultado.
Teorema 36.4. (Teorema Integral de Cauchy-Goursat generalizado para discos.)
Sean $r>0$, $z_0\in \mathbb{C}$ un punto fijo, $z_1, z_2, \ldots, z_n \in B(z_0, r)$, $D:= B(z_0, r) \setminus \{z_1, z_2, \ldots, z_n \}$ y $f:D \to \mathbb{C}$ una función analítica en $D$ tal que:
\begin{equation*}
\lim_{z\to z_j} (z-z_j)f(z)=0,
\end{equation*}para todo $j=1,\ldots, n$. Entonces:
\begin{equation*}
\int_{\gamma} f(z) dz = 0,
\end{equation*}para cualquier contorno cerrado $\gamma$ en $D$ que no pasa por los puntos $z_1, z_2, \ldots, z_n$.
Demostración. Dadas las hipótesis, es suficiente con probar el caso para un único punto $z_1\in B(z_0,r)$ en el cual $f$ no es analítica y proceder por inducción.
De manera similar a la prueba anterior, basta mostrar que existe una primitiva de $f$ en $D = B(z_0,r)\setminus\{z_1\}$. Para ello tomamos a $\zeta \in D$ y consideramos al contorno poligonal$\gamma$ que une al centro $z_0$ del disco abierto $B(z_0,r)$ con $\zeta$, considerando segmentos de recta verticales y horizontales, sin pasar por $z_1$ y definimos a dicha primitiva como la función:
\begin{equation*}
F(z)=\int_{\gamma} f(z) dz,
\end{equation*}la cual está bien definida pues $B(z_0,r)$ es poligonal conexo, entonces el contorno poligonal $\gamma$ siempre existe. Solo basta considerar la ubicación del punto $z_1\in B(z_0,r)$ al definir a $\gamma$. Si $z_1$ no cae en las rectas $x=x_0$ y $y_0$, entonces bastan tres segmentos de recta para unir a $z_0=x_0+iy_0$ con el punto $\zeta \neq z_1$, en tal caso es fácil mostrar, de la misma manera que antes, que $F_y(z)=if(z)$ y $F_x(z)=f(z)$ utilizando el lema de Goursat generalizado y concluir que $F$ es una primitiva de $f$ en $D$, por lo que el resultado se sigue de la proposición 35.2.
Por último, si $z_1$ cae en alguna de las rectas $x=x_0$ ó $y=y_0$, basta con fijar otro punto de inicio de $\gamma$, distinto del centro del disco $B(z_0,r)$, en la definición de $F$ y volver a plantear el análisis anterior.
$\blacksquare$
Observación 36.2.
Notemos que el resultado anterior es equivalente a pedir que $f$ sea analítica en $B(z_0, r) \setminus \{z_1, z_2, \ldots, z_n \}$, con $z_1, z_2, \ldots, z_n \in B(z_0, r)$, y continua en $B(z_0, r)$.
Corolario 36.1.
Sean $r>0$, $z_0\in \mathbb{C}$ un punto fijo, $[a,b]\subset\mathbb{R}$, con $a<b$, un intervalo cerrado, $f:B(z_0, r) \to \mathbb{C}$ una función analítica en el disco abierto $B(z_0, r)$, $\zeta \in B(z_0,r)$ y $\gamma:[a,b]\to B(z_0,r)$ un contorno cerrado que no pasa por $\zeta$. Entonces:
\begin{equation*}
f(\zeta) \int_{\gamma} \frac{dz}{z-\zeta} = \int_{\gamma} \frac{f(z)}{z-\zeta} dz.
\end{equation*}
Demostración.Dadas las hipótesis, sea $\zeta\in B(z_0,r)$, como $f$ es analítica en el disco abierto $B(z_0,r)$, en particular lo es en $\zeta$, por lo que:
\begin{equation*}
\lim_{z\to \zeta} \dfrac{f(z)-f(\zeta)}{z-\zeta} = f'(\zeta).
\end{equation*}
Considerando lo anterior definimos a la función:
\begin{equation*}
g(z)= \left\{ \begin{array}{lcc} \dfrac{f(z)-f(\zeta)}{z-\zeta} & \text{si} & z \neq \zeta, \\ \\ f'(\zeta) & \text{si} & z = \zeta.
\end{array} \right.
\end{equation*}
Claramente $g$ es una función analítica en $B(z_0,r)\setminus\{\zeta\}$ y continua en $\zeta$, por lo que:
\begin{equation*}
\lim_{z\to \zeta} (z-\zeta) g(z) = 0.
\end{equation*}
Entonces, por el Teorema de Cauchy generalizado tenemos que:
\begin{align*}
0 & = \int_{\gamma} g(z) dz\\
& = \int_{\gamma} \dfrac{f(z)-f(\zeta)}{z-\zeta} dz\\
& = \int_{\gamma} \dfrac{f(z)}{z-\zeta} dz – \int_{\gamma} \dfrac{f(\zeta)}{z-\zeta} dz\\
& = \int_{\gamma} \dfrac{f(z)}{z-\zeta} dz -f(\zeta) \int_{\gamma} \dfrac{dz}{z-\zeta}.
\end{align*}
Por lo que:
\begin{equation*}
f(\zeta) \int_{\gamma} \frac{dz}{z-\zeta} = \int_{\gamma} \frac{f(z)}{z-\zeta} dz,
\end{equation*} para cualquier contorno cerrado $\gamma$ en $B(z_0,r)$ que no pasa por $\zeta$.
$\blacksquare$
Lema 36.1.
Sean $[a,b]\subset\mathbb{R}$, con $a<b$, $\gamma:[a,b]\to\mathbb{C}$ un contorno y $\varphi:\mathbb{C} \to \mathbb{C}$ una función que está definida y es continua en los puntos del contorno, es decir, en $\gamma([a,b])$. Para cada $n\in\mathbb{N}^+$ se define a la función:
\begin{equation*}
F_n(z) : = \int_{\gamma} \frac{\varphi(\zeta)}{(\zeta – z)^n} d\zeta, \quad z\not\in \gamma([a,b]).
\end{equation*}
Entonces, cada función $F_n$ es analítica en $\mathbb{C}\setminus\gamma([a,b])$ y $F_n'(z) = n F_{n+1}(z)$, lo cual implica que cada $F_n$ tiene derivadas analíticas de todos los órdenes.
Demostración. Dadas las hipótesis, primero procedemos a verificar que cada función $F_n$ es continua. Sea $z_0 \in D:=\mathbb{C}\setminus\gamma([a,b])$ fijo. Como $[a,b]\subset\mathbb{R}$ es compacto y la función $\gamma$ es continua, entonces, proposición 10.9, $\gamma([a,b])$ es compacto, por lo que, proposición 10.10, $\gamma$ alcanza su valor mínimo, entonces definimos a $r:=\min\limits_{t\in[a,b]}| \gamma(t) – z_0|>0$. Análogamente, como $\gamma([a,b])$ es compacto y $\varphi$ es continua en dicho conjunto, entonces su imagen también es un conjunto compacto, en particular es un conjunto acotado, es decir, existe $M>0$ tal que $|\varphi(\zeta)| \leq M$ para todo $\zeta \in \gamma([a,b])$.
Recordemos la factorización:
\begin{equation*}
x^n – y^n = (x-y)(x^{n-1}+x^{n-2}y + \cdots +xy^{n-2}+y^{n-1}).
\end{equation*}
Entonces:
\begin{align*}
\frac{1}{(\zeta – z)^n} – \frac{1}{(\zeta – z_0)^n} & = \left[ \frac{1}{\zeta – z} – \frac{1}{\zeta – z_0}\right] \left[ \frac{1}{(\zeta – z)^{n-1}} + \frac{1}{(\zeta – z)^{n-2}(\zeta – z_0)}\right.\\
& \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\, \quad \quad \left. + \cdots + \frac{1}{(\zeta – z)(\zeta – z_0)^{n-2}} + \frac{1}{(\zeta – z_0)^{n-1}}\right]\\
& = \left(z – z_0\right)\left[ \frac{1}{(\zeta – z)^{n}(\zeta – z_0)} + \frac{1}{(\zeta – z)^{n-1}(\zeta – z_0)^2}\right.\\
& \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,\, \left. + \cdots + \frac{1}{(\zeta – z)^2(\zeta – z_0)^{n-1}} + \frac{1}{(\zeta-z)(\zeta – z_0)^{n}}\right].
\end{align*}
Multiplicando por $\varphi(\zeta)$ e integrando a lo largo de $\gamma$, en ambos lados de la igualdad anterior, tenemos que:
\begin{align*}
F_n(z)-F_n(z_0) & = (z-z_0) \int_{\gamma} \left[\frac{\varphi(\zeta)}{(\zeta – z)^{n}(\zeta – z_0)} + \cdots + \frac{\varphi(\zeta)}{(\zeta-z)(\zeta – z_0)^{n}} \right] d \zeta\\
& = (z-z_0) \int_{\gamma} \sum_{k=0}^{n-1} \frac{\varphi(\zeta)}{(\zeta – z)^{n-k}(\zeta – z_0)^{k+1}} d \zeta\\
& = (z-z_0) \sum_{k=0}^{n-1} \int_{\gamma}\frac{\varphi(\zeta)}{(\zeta – z)^{n-k}(\zeta – z_0)^{k+1}} d \zeta,\tag{36.3}
\end{align*}donde $z\in B(z_0, r/2)$ y $\zeta \in \gamma([a,b])$. Por lo que $|z-z_0| < r/2$, $r/2 < r \leq |\zeta – z_0|$ y $r/2<|\zeta – z|$, entonces:
\begin{equation*}
\left| \frac{\varphi(\zeta)}{(\zeta – z)^{n-k}(\zeta – z_0)^{k+1}} \right| < M \left(\frac{2}{r}\right)^{n+1},
\end{equation*}para cada $0\leq k \leq n-1$.
Por lo tanto, para $\varepsilon>0$, tomando $\delta < r/2$ se tiene que si $|z-z_0|<\delta$, entonces podemos acotar a (36.3) mediante la proposición 34.3(5) y la desigualdad del triángulo, es decir:
\begin{align*}
| F_n(z)-F_n(z_0)| & = |z-z_0| \left|\sum_{k=0}^{n-1} \int_{\gamma}\frac{\varphi(\zeta)}{(\zeta – z)^{n-k}(\zeta – z_0)^{k+1}} d \zeta\right|\\
& \leq |z-z_0| \sum_{k=0}^{n-1} \left| \int_{\gamma}\frac{\varphi(\zeta)}{(\zeta – z)^{n-k}(\zeta – z_0)^{k+1}} d \zeta\right|\\
& \leq |z-z_0| \sum_{k=0}^{n-1} \int_{\gamma}\left| \frac{\varphi(\zeta)}{(\zeta – z)^{n-k}(\zeta – z_0)^{k+1}} d \zeta\right|\\
& < \delta \sum_{k=0}^{n-1} M \left(\frac{2}{r}\right)^{n+1} \int_{\gamma} |dz|\\
& = n \delta M \ell(\gamma) \left(\frac{2}{r}\right)^{n+1}.
\end{align*}
Por lo que, para:
\begin{equation*}
\delta := \min \left\{\frac{r}{2}, \frac{\varepsilon r^{n+1}}{ n M \ell(\gamma) 2^{n+1}}\right\},
\end{equation*}se tiene que si $|z-z_0|\delta$, entonces $|F_n(z)-F_n(z_0)| < \varepsilon$, por lo que $F_n$ es una función continua.
Dividiendo en ambos lados de la igualdad (36.3) por $z-z_0$, tenemos que:
\begin{align*}
\frac{F_n(z)-F_n(z_0)}{z-z_0} & =\sum_{k=0}^{n-1} \int_{\gamma}\frac{\varphi(\zeta)}{(\zeta – z)^{n-k}(\zeta – z_0)^{k+1}} d \zeta\\
& =\sum_{k=0}^{n-1} \int_{\gamma}\frac{\varphi(\zeta)(\zeta – z_0)^{-(k+1)}}{(\zeta – z)^{n-k}} d \zeta.
\end{align*}
Dado que $z_0\not\in\gamma([a,b])$, entonces para cada $0\leq k \leq n-1$, la función:
\begin{equation*}
\varphi(\zeta)(\zeta – z_0)^{-(k+1)},
\end{equation*}es continua. Por lo tanto, de la primera parte de la prueba tenemos que la función:
\begin{equation*}
h(z) = \int_{\gamma}\frac{\varphi(\zeta)(\zeta – z_0)^{-(k+1)}}{(\zeta – z)^{n-k}} d \zeta,
\end{equation*}es una función continua para cada $0\leq k \leq n-1$. Entonces:
\begin{align*}
F_n'(z_0) & = \lim_{z\to z_0} \frac{F_n(z)-F_n(z_0)}{z-z_0}\\
& = \lim_{z\to z_0} \sum_{k=0}^{n-1} \int_{\gamma}\frac{\varphi(\zeta)(\zeta – z_0)^{-(k+1)}}{(\zeta – z)^{n-k}} d \zeta\\
& = \sum_{k=0}^{n-1} \int_{\gamma} \lim_{z\to z_0} \frac{\varphi(\zeta)(\zeta – z_0)^{-(k+1)}}{(\zeta – z)^{n-k}} d \zeta\\
& = \sum_{k=0}^{n-1} \int_{\gamma} \frac{\varphi(\zeta)}{(\zeta – z_0)^{n+1}} d \zeta\\
& = \sum_{k=0}^{n-1} \int_{\gamma} \frac{\varphi(\zeta)}{(\zeta – z_0)^{n+1}} d \zeta\\
& = n\int_{\gamma} \frac{\varphi(\zeta)}{(\zeta – z_0)^{n+1}} d \zeta\\
& = n F_{n+1}(z_0).
\end{align*}
$\blacksquare$
Definición 36.1. (Índice de un contorno cerrado respecto a un punto.)
Sean $[a,b]\subset\mathbb{R}$, con $a<b$, un intervalo cerrado, $\gamma:[a,b]\to\mathbb{C}$ un contorno cerrado y $z_0\in\mathbb{C}\setminus\gamma([a,b])$, es decir, $z_0\in\mathbb{C}$ es un punto que no está en el contorno $\gamma$. Se define al índice de $\gamma$ con respecto de $z_0$ como:
\begin{equation*}
n(\gamma, z_0) = \frac{1}{2\pi i} \int_{\gamma} \frac{dz}{z-z_0}.
\end{equation*}
Proposición 36.1.
Sean $[a,b]\subset\mathbb{R}$, con $a<b$, un intervalo cerrado, $\gamma:[a,b]\to\mathbb{C}$ un contorno cerrado y $z_0\in\mathbb{C}\setminus\gamma([a,b])$. Entonces:
\begin{equation*}
\int_{\gamma} \frac{1}{z-z_0} dz = 2\pi k i,\tag{36.3}
\end{equation*}para algún $k\in\mathbb{Z}$. Es decir, la integral (36.3) es un múltiplo entero de $2\pi i$.
Demostración. Dadas las hipótesis, por la definición 34.1 tenemos que:
\begin{equation*}
h(z):=\int_{\gamma} \frac{1}{z-z_0} dz = \int_{a}^{b} \frac{\gamma'(t)}{\gamma(t)-z_0} dt.
\end{equation*}
Considerando lo anterior definimos a la función híbrida $F:[a,b]\to\mathbb{C}$ como:
\begin{equation*}
F(x):= \int_{a}^{x} \frac{\gamma'(t)}{\gamma(t)-z_0} dt, \quad a\leq x \leq b.
\end{equation*}
Por construcción es claro que $F$ es una función continua en $[a,b]$ y que $F(a) =0$ y $F(b)=h(z)$. Veamos que $F(b)=2\pi k i$, para algún $k\in\mathbb{Z}$.
Dado que $\gamma’$ es continua en $[a,b]$, salvo quizás en un número finito de puntos, entonces $F$ es diferenciable en los puntos de continuidad de $\gamma’$ y su derivada está dada por el Teorema Fundamental del Cálculo:
\begin{equation*}
F'(x) = \frac{\gamma'(x)}{\gamma(x)-z_0}, \tag{36.4}
\end{equation*}para los puntos donde $\gamma’$ existe.
Sea $G:[a,b] \to\mathbb{C}$ la función híbrida dada por:
\begin{equation*}
G(t) = e^{-F(t)}\left[\gamma(t)-z_0\right], \quad a\leq t \leq b.
\end{equation*}
Por construcción tenemos que $G$ es también continua en $[a,b]$. Más aún, para cada $t\in [a,b]$ donde $\gamma’$ es continua, por (36.4) y como $\gamma(a) = \gamma(b) \neq z_0$, tenemos que:
\begin{align*}
G'(t) &= e^{-F(t)} \gamma'(t) – F'(t) e^{-F(t)}\left[\gamma(t)-z_0\right]\\
&= e^{-F(t)}\left( \gamma'(t) – F'(t)\left[\gamma(t)-z_0\right]\right)\\
&= e^{-F(t)}\left( \gamma'(t) – \frac{\gamma'(t)}{\gamma(t)-z_0}\left[\gamma(t)-z_0\right]\right)\\
&= e^{-F(t)}\left[\gamma'(t) – \gamma'(t)\right]\\
& = 0.
\end{align*}
Lo anterior nos dice que $G$ es una función constante en cada subintervalo donde $\gamma’$ existe y como $G$ es continua entonces $G$ es una función constante en $[a,b]$, por lo que $G(a) = G(b)$, es decir:
\begin{equation*}
e^{-F(a)}\left[\gamma(a)-z_0\right] = e^{-F(b)}\left[\gamma(b)-z_0\right].
\end{equation*}
Dado que $F(a) =0$ y $\gamma(a) = \gamma(b) \neq z_0$, tenemos que:
\begin{equation*}
e^{-F(b)} = 1,
\end{equation*}lo cual implica, por la proposición 20.2(10), que para algún $k\in\mathbb{Z}$:
\begin{equation*}
F(b)=2\pi k i.
\end{equation*}
Entonces:
\begin{equation*}
2\pi k i = F(b) = h(z) =\int_{\gamma} \frac{1}{z-z_0} dz,
\end{equation*}para algún $k\in\mathbb{Z}$.
$\blacksquare$
Corolario 36.2.
El índice de un contorno cerrado $\gamma$ respecto a un punto $z_0$ es un número entero.
Demostración. Es inmediato de la definición de $n(\gamma,z_0)$ y la proposición 36.1.
$\blacksquare$
Observación 36.3.
Claramente $f(z) = \dfrac{1}{z-z_0}$ es una función analítica en $D:=\mathbb{C}\setminus\{z_0\}$. Si pudiéramos encontrar una función analítica $F:D\to\mathbb{C}$ tal que $F'(z) = f(z)$ para todo $z\in D$, entonces tendríamos que $n(\gamma, z_0) = 0$ para toda curva cerrada $\gamma$ en $D$, que no pase por $z_0$. Sin embargo, de acuerdo con el ejemplo 34.1 y la proposición 35.3 sabemos que $f$ no tiene primitiva en $D$, por lo que $n(\gamma, z_0) \neq 0$ para toda curva cerrada $\gamma$ en $D$, que no pase por $z_0$.
Para continuar, en este punto es importante introducir el siguiente resultado, el cual intuitivamente es claro, pero cuya demostración es bastante complicada y se escapa de los objetivos de estas notas, por lo que en el curso lo tomaremos como válido, aunque puede consultarse una prueba formal de este hecho en:
- Complex Analysis: The Argument Principle in Analysis and Topology, de Alan F. Beardon.
- An Introduction to Classical Complex Analysis, de Robert B. Burckel.
Teorema 36.5. (Teorema de la curva de Jordan.)
Los puntos en cualquier contorno cerrado simple $C\subset\mathbb{C}$ son la frontera de dos dominios distintos, uno de los cuales es el interior de $C$, denotado por $I$, y está acotado. El otro, es el exterior de $C$, denotado por $E$, y no es acotado. En tal caso, $I \cup E \cup C$ es igual al plano complejo $\mathbb{C}$.
Ejemplo 36.3.
Sean $r>0$ y $z_0\in\mathbb{C}$ un punto fijo. Consideremos a los conjuntos disjuntos $S_1 = \{z\in\mathbb{C} : |z-z_0|<r\}$ y $S_2 = \{z\in\mathbb{C} : |z-z_0|>r\}$, los cuales son abiertos en $\mathbb{C}$. Geométricamente es claro que la circunferencia $C(z_0,r)=\{z\in\mathbb{C} : |z-z_0|=r\}$ es un contorno cerrado simple y los puntos en $C(z_0,r)$ son la frontera de $S_1$ y $S_2$. El interior de $C(z_0,r)$ es $S_1$, el cual es un conjunto acotado y el exterior de $C(z_0,r)$ es $S_2$, el cual es un conjunto no acotado.
Observación 36.4.
Por la proposición 10.9 sabemos que al ser $[a,b]\subset\mathbb{R}$, con $a<b$, un conjunto compacto y $\gamma:[a,b]\to\mathbb{C}$ una trayectoria, es decir, $\gamma$ es una función continua en $[a,b]$, entonces la curva $\gamma([a,b])$ en el plano complejo, es un conjunto compacto, es decir, una curva en $\mathbb{C}$ es un conjunto cerrado y acotado. Entonces el conjunto $U = \mathbb{C}\setminus\gamma([a,b])$ es un conjunto abierto no vacío, por lo que, ejercicio 9 de la entrada 10, podemos ver a $U$ como la unión disjunta numerable de dominios, correspondientes con las componentes conexas de $U$.
El siguiente lema enuncia algunas de las propiedades clave del índice de un contorno.
Lema 36.2.
Sean $\gamma$ un contorno cerrado en el plano complejo y $U=\mathbb{C}\setminus\gamma([a,b])$. Se cumplen las siguientes propiedades.
- $n(\gamma, z)$ permanece constante conforme $z$ toma valores en cualquiera de las componentes conexas de $U$.
- $n(\gamma, z) = 0$ para cualquier $z$ en la componente no acotada de $U$.
- Si $\gamma$ es simple, entonces $n(\gamma, z)=1$ ó $n(\gamma, z)=-1$, para todo $z$ en la componente acotada de $U$.
Demostración. Dadas las hipótesis, únicamente probaremos las primeras dos propiedades. La última afirmación está sustentada en el teorema de la curva de Jordan y por lo extenso de su prueba la omitiremos, pero se puede consultar una prueba detallada en An Introduction to Complex Function Theory, de Bruce P. Palka.
- Sea $\varphi : \gamma([a,b]) \to \mathbb{C}$ dada por:
\begin{equation*}
\varphi(\zeta) = \frac{1}{2\pi i}.
\end{equation*}Por lo que, del lema 36.1 para $n=1$ y la definición 36.1, tenemos que:
\begin{equation*}
n(\gamma,z)=\int_{\gamma} \frac{1}{\zeta-z} d\zeta,
\end{equation*}es una función analítica, de $z$, en $U$, cuya derivada está dada por:
\begin{equation*}
n'(\gamma,z)=\int_{\gamma} \frac{1}{(\zeta-z)^2} d\zeta.
\end{equation*}Por otra parte, si fijamos a $z\in\mathbb{C}$, entonces la función:
\begin{equation*}
f(\zeta) = \frac{1}{(\zeta-z)^2},
\end{equation*}es una función analítica, de $\zeta$, en $\mathbb{C}\setminus\{z\}$ y tiene como primitiva, en dicho conjunto, a la función:
\begin{equation*}
F(\zeta) = -\frac{1}{\zeta-z}.
\end{equation*}Si $z\in U$, entonces $\gamma$ es un contorno cerrado en $\mathbb{C}\setminus\{z\}$, por lo que del TFC para integrales de contorno, proposición 35.1, para $z\in U$ tenemos que:
\begin{equation*}
\int_{\gamma} \frac{1}{(\zeta-z)^2} d\zeta = \int_{\gamma} f(\zeta) d\zeta = 0.
\end{equation*}Por lo que $n'(\gamma,z) = 0$ en $U$, entonces de la proposición 19.2 concluimos que $n(\gamma,z)$ es una función constante en cada componente de $U$. - Sea $r>0$ tal que el conjunto compacto $\gamma([a,b])$ está contenido en el disco abierto $B(0,r)$. Tenemos que el conjunto $\mathbb{C}\setminus B(0,r)$ es un subconjunto conexo de $U$, entonces por la proposición 10.6(1) se cumple que dicho conjunto conexo está contenido en alguna componente conexa $D$ de $U$. Notemos que la componente conexa $D$ es la única componente no acotada de $U$, ya que todas las demás componentes claramente subconjuntos de $B(0,r)$.
Como el punto $z_0=2r \in D$ y la función $f(\zeta) = (\zeta – z_0)^{-1}$ es analítica en $B(0,r)$, por el teorema (local) integral de Cauchy, teorema 36.3, tenemos que:
\begin{equation*}
n(\gamma,z_0)= \frac{1}{2\pi i}\int_{\gamma} \frac{1}{\zeta-z} d\zeta = 0.
\end{equation*}Entonces, por el inciso anterior tenemos que $n(\gamma,z) = 0$ para todo $z\in D$.
$\blacksquare$
Observación 36.5.
De acuerdo con lo anterior, el índice de un contorno $n(\gamma,z_0)$ tiene una interpretación geométrica clara, ya que nos dice el número de vueltas que el contorno cerrado $\gamma$ le da al punto $z_0$ y su signo está determinado por la orientación del contorno, es decir, si $\gamma$ tiene orientación positiva entonces $n(\gamma,z_0)$ es positivo, mientras que si $\gamma$ tiene orientación negativa entonces $n(\gamma,z_0)$ es negativo.
Más aún, si el contorno cerrado $\gamma$ es simple y el punto $z_0$ está en el interior de $\gamma$, entonces $n(\gamma,z_0)=1$, mientras que si $z_0$ está fuera del contorno entonces $n(\gamma,z_0)=0$.
Motivados en lo anterior establecemos la siguiente definición, la cual es consistente con el teorema de la curva de Jordan.
Definición 36.2. (Interior de un contorno cerrado simple.)
Sean $[a,b]\subset\mathbb{R}$, con $a<b$, y $\gamma: [a,b]\to\mathbb{C}$ un contorno cerrado simple en $\mathbb{C}$. Se define al interior de $\gamma$ como el conjunto:
\begin{equation*}
I(\gamma):= \{z\in\mathbb{C} : n(\gamma,z) \neq 0\}.
\end{equation*}
Algunas de las propiedades más elementales del índice de un contorno están dadas en la siguiente:
Proposición 36.2. (Propiedades del índice de un contorno.)
Sean $[a,b]\subset\mathbb{R}$, con $a<b$, y $\gamma, \beta: [a,b]\to\mathbb{C}$ dos contornos cerrados en $\mathbb{C}$ con el mismo punto inicial. Se cumplen las siguientes propiedades.
- $n(-\gamma,z) = -n(\gamma,z)$, para todo $z\in\mathbb{C}\setminus\gamma([a,b])$.
- $n(\gamma+\beta,z) = n(\gamma,z)+n(\beta,z)$, para todo $z\in\mathbb{C}\setminus\left(\gamma([a,b]) \cup \beta([a,b])\right)$.
- $n(\overline{\gamma},\overline{z}) = -n(\gamma,z)$, para todo $z\in\mathbb{C}\setminus\gamma([a,b])$.
- n(a\gamma+b,az+b) = n(\gamma,z)$, para todo $z\in\mathbb{C}\setminus\gamma([a,b])$, con $a\neq 0$ y $b$ dos constantes.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Ejemplo 36.4.
Sean $r>0$ y $z_0\in\mathbb{C}$ un punto fijo. Consideremos a la circunferencia $C(z_0,r)$ y al disco abierto $B(z_0,r)$.
a) Sea $\gamma:[0,2\pi] \to \mathbb{C}$ dada por $\gamma(t)=z_0 + re^{it}$, es decir, $\gamma$ parametriza a la circunferencia $C(z_0,r)$ positivamente. Si $z\in B(z_0,r)$, entonces por el lema 36.2(1), la definición 36.1 y el ejemplo 34.1(a) tenemos que:
\begin{align*}
n(\gamma,z) & = n(\gamma,z_0)\\
& = \frac{1}{2\pi i} \int_{\gamma} \frac{1}{\zeta – z_0} d\zeta\\
& = \frac{1}{2\pi i} 2\pi i\\
& = 1.
\end{align*}
Más aún, por el lema 36.2(2), tenemos que si $z\in \mathbb{C} \setminus B(z_0,r)$, entonces $n(\gamma,z) = 0$.
b) Sea $\gamma:[0,2\pi] \to \mathbb{C}$ dada por $\gamma(t)=z_0 + re^{-it}$, es decir, $\gamma$ parametriza a la circunferencia $C(z_0,r)$ negativamente. Si $z\in B(z_0,r)$, entonces por el lema 36.2(1), la definición 36.1 y la definición 34.1 tenemos que:
\begin{align*}
n(\gamma,z) & = n(\gamma,z_0)\\
& = \frac{1}{2\pi i} \int_{\gamma} \frac{1}{\zeta – z_0} d\zeta\\
& = \frac{1}{2\pi i} \int_{0}^{2\pi} \frac{\gamma'(t)}{\gamma(t) – z_0} dt\\
& = \frac{1}{2\pi i} \int_{0}^{2\pi} \frac{-ire^{-it}}{z_0 + re^{-it} – z_0} dt\\
& = -\frac{i}{2\pi i} \int_{0}^{2\pi} dt\\
& = -\frac{i}{2\pi i} 2\pi\\
& = -1.
\end{align*}
Del lema 36.2(2), se sigue que para $z\in \mathbb{C} \setminus B(z_0,r)$, se cumple que $n(\gamma,z) = 0$.
c) Sea $\gamma:[0,2\pi n] \to \mathbb{C}$, con $n\in\mathbb{N}^+$, dada por $\gamma(t)=z_0 + re^{it}$, es decir, $\gamma$ parametriza a la circunferencia $C(z_0,r)$ positivamente, pero la recorre $n$-veces. Si $z\in B(z_0,r)$, entonces por el lema 36.2(1), la definición 36.1 y la definición 34.1 tenemos que:
\begin{align*}
n(\gamma,z) & = n(\gamma,z_0)\\
& = \frac{1}{2\pi i} \int_{\gamma} \frac{1}{\zeta – z_0} d\zeta\\
& = \frac{1}{2\pi i} \int_{0}^{2\pi n} \frac{\gamma'(t)}{\gamma(t) – z_0} dt\\
& = \frac{1}{2\pi i} \int_{0}^{2\pi n} \frac{ire^{-it}}{z_0 + re^{-it} – z_0} dt\\
& = \frac{i}{2\pi i} \int_{0}^{2\pi n} dt\\
& = \frac{i}{2\pi i} 2\pi n\\
& = n.
\end{align*}
Más aún, por el lema 36.2(2), tenemos que si $z\in \mathbb{C} \setminus B(z_0,r)$, entonces $n(\gamma,z) = 0$.
De acuerdo con los resultados previos, estamos listos para establecer una de las primeras consecuencias del teorema integral de Cauchy generalizado, para discos, mediante el cual podremos obtener una representación fundamental de una función analítica.
Proposición 36.3. (Fórmula integral de Cauchy para discos.)
Sean $r>0$, $z_0\in \mathbb{C}$ un punto fijo, $f:B(z_0, r) \to \mathbb{C}$ una función analítica en el disco abierto $B(z_0, r)$ y $\gamma$ un contorno cerrado en $B(z_0,r)$. Entonces:
\begin{equation*}
n(\gamma, z) f(z) = \frac{1}{2\pi i}\int_{\gamma} \frac{f(\zeta)}{\zeta-z} d\zeta,
\end{equation*}para todo $z \in B(z_0,r)\setminus\gamma([a,b])$.
Demostración. Dadas las hipótesis, fijamos un punto $z \in B(z_0,r)\setminus\gamma([a,b])$. Definimos a la función:
\begin{equation*}
g:B(z_0,r)\to\mathbb{C},
\end{equation*} como:
\begin{equation*}
g(\zeta)= \left\{ \begin{array}{lcc} \dfrac{f(\zeta) – f(z)}{\zeta – z} & \text{si} & \zeta \neq z, \\ \\ f'(z) & \text{si} & \zeta = z, \end{array} \right.
\end{equation*}donde $\zeta$ es una variable independiente.
Es claro que $g$ es una función analítica en $B(z_0,r)\setminus\{z\}$. Más aún, como $f$ es analítica en $B(z_0,r)$, entonces:
\begin{equation*}
\lim_{\zeta \to z} g(\zeta) = \lim_{\zeta \to z} \dfrac{f(\zeta) – f(z)}{\zeta – z} = f'(z) = g(z),
\end{equation*}es decir, $g$ es continua en $z$, por lo que:
\begin{equation*}
\lim_{\zeta \to z} (\zeta – z) g(\zeta) = 0.
\end{equation*}
Como $z$ no está en el contorno cerrado $\gamma$, del teorema 36.4 y la definición 36.1, tenemos que:
\begin{align*}
0 & = \int_{\gamma} g(\zeta) d\zeta\\
& = \int_{\gamma} \dfrac{f(\zeta) – f(z)}{\zeta – z} d\zeta\\
& = \int_{\gamma} \dfrac{f(\zeta)}{\zeta – z} d\zeta – \int_{\gamma} \dfrac{f(z)}{\zeta – z} d\zeta\\
& = \int_{\gamma} \dfrac{f(\zeta)}{\zeta – z} d\zeta – 2\pi i \, n(\gamma,z) f(z),
\end{align*}es decir:
\begin{equation*}
n(\gamma,z) f(z) = \frac{1}{2\pi i}\int_{\gamma} \dfrac{f(\zeta)}{\zeta – z} d\zeta.
\end{equation*}Dado que $z \in B(z_0,r)\setminus\gamma([a,b])$ es arbitrario, entonces se tiene el resultado.
$\blacksquare$
Observación 36.6.
Un aspecto importante de la fórmula integral de Cauchy es que para un punto $z\in\mathbb{C}$ para el cual $n(\gamma, z)\neq 0$, podemos expresar el valor de la función $f(z)$ de manera explícita en términos de los valores de $f$ que se encuentran en el contorno $\gamma$, a cierta distancia de $z$.
La aplicación más usual de la fórmula integral de Cauchy se tiene para el caso en que $n(\gamma, z)=1$, ya que bajo dicha condición se tiene que:
\begin{equation*}
f(z) = \frac{1}{2\pi i}\int_{\gamma} \frac{f(\zeta)}{\zeta-z} d\zeta.
\end{equation*}
Ejemplo 36.5.
Evaluemos la integral:
\begin{equation*}
\int_{\gamma} \frac{e^{\pi z}}{z^3+z} dz,
\end{equation*}donde $\gamma$ parametriza positivamente a la circunferencia $C(0,2)$.
Solución. Primeramente parametrizamos a la circunferencia $C(0,2)$ como $\gamma(t)=2e^{it}$, con $0\leq t\leq 2\pi$.
Aplicando fracciones parciales tenemos que:
\begin{equation*}
\frac{e^{\pi z}}{z^3+z} = \frac{e^{\pi z}}{z} – \frac{e^{\pi z}}{2(z-i)} – \frac{e^{\pi z}}{2(z+i)}.
\end{equation*}
Notemos que para todo $z\in B(0,2)$, por el ejemplo 36.4(a), se cumple que:
\begin{equation*}
n(\gamma,z) = n(\gamma,0) = 1.
\end{equation*}
Sea $f(z)= e^{\pi z}$. Claramente $f$ es una función entera, por lo que para $r>2$, se cumple que $C(0,2) \subset B(0,r)$ y $f$ es analítica en $B(0,r)$. Entonces, de la fórmula integral de Cauchy para discos, como $0,i, -i \in B(0,2) \subset B(0,r)$, tenemos que:
\begin{align*}
\int_{\gamma} \frac{e^{\pi \zeta}}{\zeta} d\zeta = \int_{\gamma} \frac{e^{\pi \zeta}}{\zeta – 0} d\zeta & = 2\pi i \, n(\gamma, 0) f(0)\\
& = 2\pi i (1)(e^{0})\\
& = 2\pi i.
\end{align*}
\begin{align*}
\int_{\gamma} \frac{e^{\pi \zeta}}{2(\zeta-i)} d\zeta = \frac{1}{2} \int_{\gamma} \frac{e^{\pi \zeta}}{\zeta – i} d\zeta & = \frac{2\pi i \, n(\gamma, i) f(i)}{2}\\
& = \frac{2\pi i (1)(e^{i\pi})}{2}\\
& = -\pi i.
\end{align*}
\begin{align*}
\int_{\gamma} \frac{e^{\pi \zeta}}{2(\zeta+i)} d\zeta = \frac{1}{2} \int_{\gamma} \frac{e^{\pi \zeta}}{\zeta + i} d\zeta & = \frac{2\pi i \, n(\gamma, -i) f(-i)}{2}\\
& = \frac{2\pi i (1)(e^{-i\pi})}{2}\\
& = -\pi i.
\end{align*}
De la proposición 34.2(1) tenemos que:
\begin{align*}
\int_{\gamma} \frac{e^{\pi \zeta}}{\zeta^3+\zeta} d\zeta & = \int_{\gamma} \frac{e^{\pi \zeta}}{\zeta}d\zeta – \int_{\gamma} \frac{e^{\pi \zeta}}{2(\zeta-i)} d\zeta -\int{\gamma} \frac{e^{\pi \zeta}}{2(\zeta+i)} d\zeta\\
& = 2\pi i – (-i\pi) – (-i\pi)\\
& = 4\pi i.
\end{align*}
Por lo que:
\begin{equation*}
\int_{\gamma} \frac{e^{\pi z}}{z^3+z} dz = 4\pi i.
\end{equation*}
Ejemplo 36.6.
Veamos que:
\begin{equation*}
\int_{\gamma} \frac{e^{i\pi z}}{2z^2-5z+2} dz = \frac{2\pi}{3},
\end{equation*}donde $\gamma$ es la circunferencia unitaria $C(0,1)$, orientada positivamente.
Solución. Tenemos que $\gamma(t) = e^{it}$, para $0\leq t\leq 2\pi$, parametriza a la circunferencia unitaria $C(0,1)$, positivamente. Factorizando el denominador del integrando, tenemos que $2z^2-5z+2 = (2z-1)(z-2)$, es decir, $z_0=1/2$ y $z_1 = 2$ son las raíces de dicho polinomio complejo. Como $1/2$ está en el interior de $\gamma$, por el lema 36.2(1) y el ejemplo 36.4(a), concluimos que:
\begin{equation*}
n(\gamma, 1/2) = n(\gamma, 0) = 1.
\end{equation*}
Sea $f(z) = \dfrac{e^{i\pi z}}{z-2}$. Claramente $f$ es analítica en $D=\mathbb{C}\setminus\{2\}$, por lo que es analítica en $B(0,2)\subset D$ y $\gamma$ está completamente contenida en $D$, entonces, por la fórmula integral de Cauchy (para discos), tenemos que:
\begin{align*}
\int_{\gamma} \frac{e^{i\pi z}}{2z^2-5z+2} dz & = \int_{\gamma} \frac{e^{i\pi z}}{(2z-1)(z-2)}dz\\
& = \int_{\gamma} \frac{f(z)}{2z-1} dz\\
& = \frac{1}{2} \int_{\gamma} \frac{f(z)}{z-1/2} dz\\
& = \pi i \, n(\gamma,1/2) f(1/2)\\
& = \pi i (1) \frac{e^{i \pi/2}}{\frac{1}{2} – 2}\\
& = \frac{2\pi}{3}.
\end{align*}
Procedemos ahora a establecer una consecuencia de la fórmula integral de Cauchy, la cual nos deja ver claramente las diferencias entre el Cálculo Complejo y el Cálculo Real.
Proposición 36.4.
Sean $U\subset\mathbb{C}$ un conjunto abierto y $f:U \to \mathbb{C}$ una función analítica en $U$. Entonces $f’$ también es analítica en $U$. En particular $f\in C^{1}(U)$.
Demostración. Dadas las hipótesis, basta probar que cada $z_0\in U$ es el centro de algún disco abierto $D$ en el cual $f’$ es analítica, por lo que $f^{(2)}(z_0) = (f’)'(z_0)$ existe.
Sean $z_0 \in U$ fijo y $r>0$ tal que $B(z_0,r) \subset U$. Fijamos a $s$ tal que $0<s<r$ y definimos a $D = B(z_0,s)$. Por la fórmula integral de Cauchy para discos, aplicada al disco $B(z_0,r)$ y al contorno $\gamma = \partial D$ orientado positivamente, es decir, $\gamma(t)=z_0+se^{it}$, con $0\leq t\leq 2\pi$, tenemos que:
\begin{equation*}
f(z) = \frac{1}{2\pi i} \int_{\gamma} \frac{f(\zeta)}{\zeta – z} d \zeta, \quad \forall z\in D.
\end{equation*}
Del lema 36.2(1) se sigue que:
\begin{equation*}
n(\gamma,z) = n(\gamma,z_0) = \frac{1}{2\pi i} \int_{0}^{2\pi} \frac{ise^{it}}{se^{it}} dt = 1,
\end{equation*}para todo $z\in D$.
Sea $\varphi:\gamma([0,2\pi]) \to \mathbb{C}$ dada por:
\begin{equation*}
\varphi(\zeta) = \frac{f(\zeta)}{2\pi i}.
\end{equation*}
Del lema 36.1, aplicado a $\varphi$ para el caso $n=1$, tenemos que:
\begin{equation*}
F_1(z) = \frac{1}{2\pi i} \int_{\gamma} \frac{f(\zeta)}{\zeta – z} d \zeta = f(z), \quad \forall z\in D,
\end{equation*}por lo que:
\begin{equation*}
f'(z) = \frac{1}{2\pi i} \int_{\gamma} \frac{f(\zeta)}{(\zeta – z)^2} d \zeta,
\end{equation*}para todo $z \in D$. Aplicando el lema 36.1, para el caso $n=2$, tenemos que:
\begin{equation*}
f'(z) = F_1′(z) = F_2(z),
\end{equation*}donde $F_2$ es una función analítica en $\mathbb{C}\setminus\gamma([0,2\pi])$. Por lo tanto, $f’$ es analítica en $D\subset\mathbb{C}\setminus\gamma([0,2\pi])$.
Como $z_0 \in U$ es arbitrario, entonces $f$ es analítica en $U$.
Por último, dado que $f$ es analítica en $U$, para $f(z)=u(x,y)+iv(x,y)$, por el teorema 17.1 tenemos que existen las derivadas parciales $u_x, u_y, v_x$ y $v_y$ y satisfacen las ecuaciones de C-R en $U$, es decir:
\begin{equation*}
f'(z) = f_x = i f_y,
\end{equation*}y como $f’$ es analítica en $U$, en particular es continua en $U$, por lo que las derivadas parciales $u_x, u_y, v_x$ y $v_y$ son continuas en $U$ y por tanto $f\in C^{1}(U)$.
$\blacksquare$
Corolario 36.3.
Sean $U\subset\mathbb{C}$ un conjunto abierto y $f:U \to \mathbb{C}$ una función analítica en $U$. Entonces $f$ es indefinidamente diferenciable en $U$ y todas las derivadas $f’, f^{(2)}, \ldots, f^{(k)}, \ldots$, también son funciones analíticas en $U$. En particular $f\in C^{\infty}(U)$.
Demostración. Se sigue del resultado anterior al aplicar inducción, por lo que los detalles se dejan como ejercicio al lector.
$\blacksquare$
Proposición 36.5. (Fórmula integral de Cauchy para derivadas, en discos.)
Sean $[a,b]\subset\mathbb{R}$, con $a<b$, un intervalo cerrado, $z_0\in\mathbb{C}$ fijo, $r>0$, $f:B(z_0,r) \to \mathbb{C}$ una función analítica en el disco abierto $B(z_0,r)$ y $\gamma:[a,b]\to B(z_0,r)$ un contorno cerrado en $B(z_0,r)$. Entonces, para todo $n\in\mathbb{N}$:
\begin{equation*}
n(\gamma, z) f^{(n)}(z) = \frac{n!}{2\pi i}\int_{\gamma} \frac{f(\zeta)}{(\zeta – z)^{n+1}} d\zeta,
\end{equation*}para todo $z\in B(z_0,r)\setminus\gamma([a,b])$.
Demostración. Dadas las hipótesis, procedemos por inducción sobre $n$. Para $n=0$ tenemos que $f^{(0)}=f$, por lo que el resultado se sigue de la fórmula integral de Cauchy (para discos), proposición 36.3, para toda función analítica en $B(z_0,r)$. Supongamos que el resultado se cumple para algún $n\in\mathbb{N}$ fijo. Verifiquemos que el resultado se cumple para $n+1$.
Como $f$ es analítica en $B(z_0,r)$, por la proposición 36.4, tenemos que $f’$ también es analítica en $B(z_0,r)$. Sea $z\in B(z_0,r)\setminus\gamma([a,b])$ fijo, entonces por hipótesis de inducción, aplicada a $f’$, tenemos que:
\begin{equation*}
n(\gamma, z) f^{(n+1)}(z) = n(\gamma, z) (f’)^{(n)}(z) = \frac{n!}{2\pi i}\int_{\gamma} \frac{f'(\zeta)}{(\zeta – z)^{n+1}} d\zeta. \tag{36.5}
\end{equation*}
Sea $g:B(z_0,r)\setminus\{z\} \to\mathbb{C}$ dada por:
\begin{equation*}
g(\zeta) = \frac{f(\zeta)}{(\zeta – z)^{n+1}}.
\end{equation*}
Es claro que $g$ es analítica en $B(z_0,r)\setminus\{z\}$ y su derivada es:
\begin{equation*}
g'(\zeta) = \frac{f'(\zeta)}{(\zeta – z)^{n+1}} – \frac{(n+1)f(\zeta)}{(\zeta – z)^{n+2}}.
\end{equation*}
Notemos que $g’$ es una función continua en $B(z_0,r)\setminus\{z\}$ y tiene como primitiva a $g$, por lo que del TFC para integrales de contorno, proposición 35.1, y la proposición 34.2(1), tenemos que:
\begin{align*}
0 & = \int_{\gamma} g'(\zeta) d\zeta\\
& = \int_{\gamma} \frac{f'(\zeta)}{(\zeta – z)^{n+1}} d\zeta – (n+1) \int_{\gamma} \frac{f(\zeta)}{(\zeta – z)^{n+2}} d\zeta,
\end{align*}es decir:
\begin{equation*}
\int_{\gamma} \frac{f'(\zeta)}{(\zeta – z)^{n+1}} d\zeta = (n+1) \int_{\gamma} \frac{f(\zeta)}{(\zeta – z)^{n+2}} d\zeta. \tag{36.6}
\end{equation*}
Entonces, de (36.5) y (36.6) se sigue que:
\begin{align*}
n(\gamma, z) f^{(n+1)}(z) & = \frac{n!}{2\pi i}\int_{\gamma} \frac{f'(\zeta)}{(\zeta – z)^{n+1}} d\zeta\\
& = \frac{n!}{2\pi i} (n+1) \int_{\gamma} \frac{f(\zeta)}{(\zeta – z)^{n+2}} d\zeta\\
& = \frac{(n+1)!}{2\pi i} \int_{\gamma} \frac{f(\zeta)}{(\zeta – z)^{n+2}} d\zeta.
\end{align*}
Dado que $z\in B(z_0,r)\setminus\gamma([a,b])$ es arbitrario y $f$ una función arbitraria, analítica en $B(z_0,r)$, entonces para todo $n\in\mathbb{N}$ y $z\in B(z_0,r)\setminus\gamma([a,b])$ se cumple que:
\begin{equation*}
n(\gamma, z) f^{(n)}(z) = \frac{n!}{2\pi i}\int_{\gamma} \frac{f(\zeta)}{(\zeta – z)^{n+1}} d\zeta.
\end{equation*}
$\blacksquare$
Ejemplo 36.7.
Sea $B(z_0,r) \subset\mathbb{C}$ un disco abierto y $f:B(z_0,r) \to\mathbb{C}$ una función analítica en dicho disco. Si $\gamma$ es un contorno cerrado contenido en $B(z_0,r)$ y $\zeta$ es un punto en el interior de $\gamma$ veamos que:
\begin{equation*}
\frac{1}{n!} \int_{\gamma} \frac{f^{(n)}(z)}{z-\zeta} dz = \int_{\gamma} \frac{f(z)}{(z-\zeta)^{n+1}} dz.
\end{equation*}
Solución. Como la función $f$ es analítica en $B(z_0,r)$, entonces $f^{(n)}$ es analítica $B(z_0,r)$. Por la fórmula integral de Cauchy tenemos que:
\begin{equation*}
n(\gamma,\zeta) f^{(n)}(\zeta) = \frac{1}{2\pi i}\int_{\gamma} \dfrac{f^{(n)}(z)}{z-\zeta} dz.
\end{equation*}
Por otra parte, de la fórmula integral de Cauchy para derivadas tenemos que:
\begin{equation*}
n(\gamma,\zeta) f^{(n)}(\zeta) = \frac{n!}{2\pi i}\int_{\gamma} \dfrac{f(z)}{(z-\zeta)^{n+1}} dz.
\end{equation*}
Entonces:
\begin{equation*}
\frac{1}{n!} \int_{\gamma} \frac{f^{(n)}(z)}{z-\zeta} dz = \int_{\gamma} \frac{f(z)}{(z-\zeta)^{n+1}} dz.
\end{equation*}
Ejemplo 36.8.
Veamos que:
\begin{equation*}
\int_{\gamma} \frac{e^{z^2}}{(z-i)^4} dz = -\frac{4\pi}{3e},
\end{equation*}donde $\gamma$ es la circunferencia $C(0,2)$ con orientación positiva.
Solución. Tenemos que $\gamma(t) = 2e^{it}$, para $0\leq t\leq 2\pi$, parametriza a la circunferencia $C(0,2)$, positivamente. Como $i$ está en el interior de $\gamma$, por el lema 36.2(1) y el ejemplo 36.4(a), concluimos que:
\begin{equation*}
n(\gamma, i) = n(\gamma, 0) = 1.
\end{equation*}
Sea $f(z) = e^{z^2}$. Claramente $f$ es una función entera, por lo que en particular es analítica en cualquier disco abierto $B(0,r)$, con $r>2$. Utilizando las reglas de derivación tenemos que:
\begin{equation*}
f^{(3)}(z) = (12z+8z^3)e^{z^2}.
\end{equation*}
Como $\gamma$ está completamente contenida en el disco abierto $B(0,r)$, con $r>2$, entonces, por la fórmula integral de Cauchy para derivadas (en discos), tenemos que:
\begin{align*}
\int_{\gamma} \frac{e^{z^2}}{(z-i)^4} dz & = \frac{2\pi i}{3!} n(\gamma,i) f^{(3)}(i)\\
& = \frac{\pi i}{3} (1) \left[12i+8i^3\right]e^{i^2}\\
& = \frac{\pi i }{3e} (4i)\\
& = – \frac{4\pi}{3e}.
\end{align*}
Tarea moral
- Determina el valor de las siguientes integrales, donde cada circunferencia está orientada positivamente.
a) $\displaystyle \int_{C(0,1)} (z^2+2z)^{-1} dz$.
b) $\displaystyle \int_{C(-i,3/2)} (z^4+z^2)^{-1} dz$. - Sea $b>0$. Muestra que:
\begin{equation*}
\int_{-\infty}^{\infty} e^{-t^2} \operatorname{cos}(2b\pi t)dt = \sqrt{\pi} e^{-b^2\pi^2}.
\end{equation*}
Hint: Considera la integral:
\begin{equation*}
\int_{\partial R} e^{-z^2} dz,
\end{equation*}donde $R$ es el rectángulo con vértices en $-c, c, c+b\pi i$ y $-c+b\pi i$, para $c>0$. - Evalúa las siguientes integrales, donde cada circunferencia está orientada positivamente.
a) $\displaystyle \int_{C(0,1)} \operatorname{Log}(z+e) z^{-1} dz$.
b) $\displaystyle \int_{C(0,2)} e^z(z+1)^{-2} dz$. - Muestra que:
\begin{equation*}
\int_{0}^{\infty} t^{-1} \operatorname{sen}(t)dt = \frac{\pi}{2}.
\end{equation*}
Hint: Considera la integral:
\begin{equation*}
\int_{\gamma} z^{-1} e^{iz} dz,
\end{equation*},donde el contorno de integración está dado por $\gamma=[s,r] + \gamma_r + [-r,-s] -\gamma_s$, para $0<s<r<\infty$, $\gamma_r(t)=re^{it}$ y $\gamma_s(t)=se^{it}$, ambas con $t\in[0,\pi]$. - Para $k\in\mathbb{N}^+$, define:
\begin{equation*}
I_k := \int_{\gamma_k} \frac{\operatorname{sen}(z)}{z} dz,
\end{equation*}donde $\gamma_k(t) = e^{t+it}$, para $t\in[-2\pi k, 2\pi k]$. Determina el $\lim\limits_{k\to \infty} I_k$.
Hint: Usa el ejercicio anterior. - Demuestra la proposición 36.2.
- Sea $\gamma = \gamma_1+\gamma_2+\gamma_3$, donde $\gamma_1(t)=e^{it}$, con $0\leq t\leq 2\pi$, $\gamma_2(t)=-1+2e^{-2it}$, con $0\leq t\leq 2\pi$ y $\gamma_3(t)=1-i+e^{it}$, con $\pi/2\leq t\leq 9\pi/2$. Determina todos los valores que toma $n(\gamma,z)$ para $z\in \mathbb{C}\setminus\gamma$.
Más adelante…
En esta entrada hemos probado algunos resultado importantes sobre las integrales de contorno como el Teorema Fundamental del Cálculo para el caso complejo y el lema de Goursat, que como veremos nos permitirá probar el Teorema de Cauchy para el caso en que se tiene un contorno cerrado arbitrario.
En la siguiente entrada probaremos algunas versiones del Teorema integral de Cauchy y abordaremos algunas de sus consecuencias más importantes, como la Fórmula Integral de Cauchy, el Teorema de Liouville, el Teorema Fundamental del Álgebra, entre otros. Además veremos un recíproco del Teorema de Cauchy conocido como el Teorema de Morera.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Integrales de contorno II.
- Siguiente entrada del curso: Consecuencias del teorema integral de Cauchy.