Introducción
En la sección anterior vimos las series y los coeficientes de Fourier para aproximar una función $f(x)$, en esta sección veremos las series de Fourier para las funciones para e impares, para esto veremos la proposición siguiente.
Series de Fourier de funciones pares e impares
Proposición. Si $f:[-a, a]\rightarrow\mathbb{R}$ es integrable, se puede asegurar que:
a) Si $f$ es par entonces:
$$\int_{-a}^{a}f(x)dx=2\int_{0}^{a}f(x)dx \tag{1}$$
b) Si $f$ es impar entonces:
$$\int_{-a}^{a}f(x)dx=0 \tag{2}$$
Demostración:
a) Recordemos que las funciones pares se tiene la propiedad que: $f(x)=f(-x)$, así tenemos que:
$$\int_{-a}^{a}f(x)dx=\int_{-a}^{0}f(x)dx+\int_{0}^{a}f(x)dx$$
Si hacemos el cambio de variable $-t=x \Rightarrow -dt=dx$ en la penúltima integral entonces:
$$\int_{-a}^{0}-f(-t)dt+\int_{0}^{a}f(x)dx=\int_{0}^{a}f(t)dt+\int_{0}^{a}f(x)dx=2\int_{0}^{a}f(x)dx$$
$\square$
b) Recordemos que las funciones impares se tiene la propiedad que $-f(x)=f(-x)$, se tiene que:
$$\int_{-a}^{a}f(x)dx=\int_{-a}^{0}f(x)dx+\int_{0}^{a}f(x)dx$$
Análogamente, hacemos el cambio de variable $t=-x \Rightarrow dt=-dx$, tenemos que:
$$\int_{a}^{0}-f(-t)dt+\int_{0}^{a}f(x)dx=-\int_{0}^{a}f(t)dt+\int_{0}^{a}f(x)dx=0$$
$\square$
Recordando que la serie de Fourier de una función $f(x)$ esta dada como:
$$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left [a_{n}\cos\left ( \frac{2n\pi }{T}x \right )+b_{n}\sin\left ( \frac{2n\pi }{T}x \right ) \right ]$$
Donde:
$a_{0}$, $a_{n}$ y $b_{n}$ se denomina coeficientes de Fourier que se definen como:
$$a_{0}=\frac{2}{T}\int_{\frac{-T}{2}}^{\frac{T}{2}}f(x)dx$$
$$a_{n}=\frac{2}{T}\int_{\frac{-T}{2}}^{\frac{T}{2}}f(x)\cos\left ( \frac{2n\pi }{T}x \right )dx $$
$$b_{n}=\frac{2}{T}\int_{\frac{-T}{2}}^{\frac{T}{2}}f(x)\sin\left ( \frac{2n\pi }{T}x \right )dx $$
Por tanto cuando $f$ es par, al calcular los coeficientes de $a_{n}$, las funciones a integrar son funciones pares, ya que tanto $f$ como las funciones coseno lo son y el producto de dos funciones pares es una función par, sin embargo, al calcular los coeficientes de $b_{n}$ las funciones a integrar es impar, porque $f$ es par y las funciones seno son impares, puesto que el producto de una función par con una función impar da como resultado una función impar por lo que utilizando las relaciones $(1)$ y $(2)$, resulta que:
$$a_{n}=\frac{4}{T}\int_{0}^{\frac{T}{2}}f(x)\cos\left ( \frac{2\pi nx}{T} \right )dx$$
$$y$$
$$b_{n}=0 $$
Por lo tanto, la serie de Fourier de una función $f(x)$ par, es una serie cosenoidal:
$$f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}a_{n}\cos\left ( \frac{2\pi nx}{T} \right )$$
Ahora, si $f$ es impar, al calcular los coeficientes $a_{n}$ las funciones a integrar son funciones impares, ya que $f$ es impar y las funciones coseno son pares; sin embargo, al calcular $b_{n}$ las funciones a integrar son pares, ya que el producto de una función impar con otra función impar da como resultado una función par, por lo que:
$$a_{n}=0 \space \space \space \space n=0 ,1, 2, 3, …..$$
$$y$$
$$b_{n}=\frac{4}{T}\int_{0}^{\frac{T}{2}}f(x)\sin\left ( \frac{2\pi nx}{T} \right )dx$$
Y la serie de Fourier de una función $f(x)$ impar es una serie senoidal:
$$f(x)=\sum_{n=1}^{\infty}b_{n}\sin\left ( \frac{2\pi nx}{T} \right )$$
Ejemplo
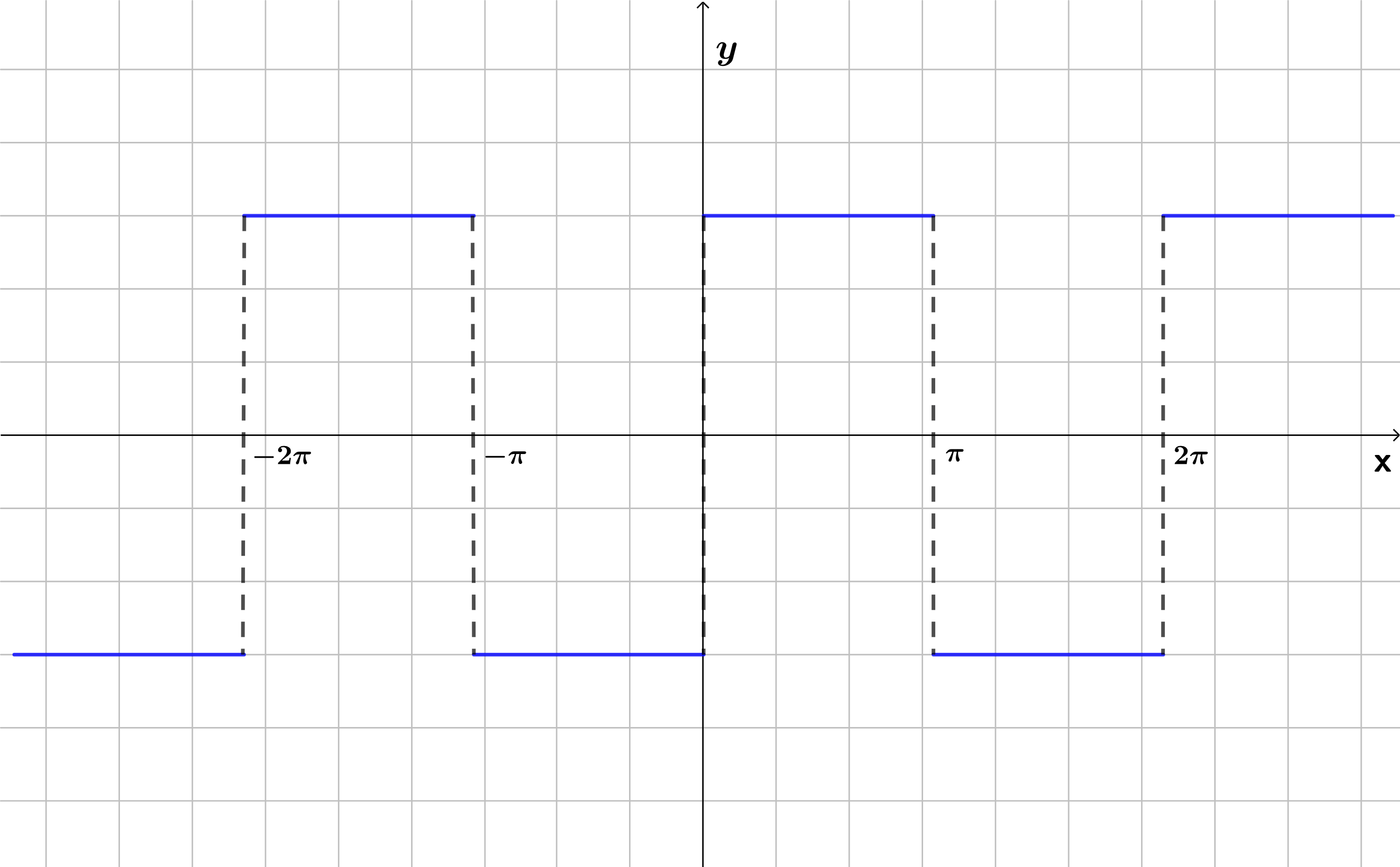
Encuentre la serie de Fourier de la siguiente función:
$$f(x)=\left\lbrace\begin{array}{c} -3 \space \space \space si \space \space \space -\pi \leq x < 0 \\ 3 \space \space \space si \space \space \space 0 \leq x < \pi \end{array}\right.$$
De la gráfica (figura $(1)$), vemos que la función es periódica con $T=2\pi$ y que la función es impar, por tanto, por lo visto anteriormente, tenemos que:
$$a_{n}=0$$
$$y$$
$$a_{0}=0$$
Por lo que solo calculamos los coeficientes $b_{n}$ como sigue:
$$b_{n}=\frac{4}{T}\int_{0}^{\frac{T}{2}}f(x)\sin\left ( \frac{2\pi nx}{T} \right )dx=\frac{4}{2\pi}\int_{0}^{\frac{2\pi}{2}}f(x)\sin\left ( \frac{2\pi nx}{2\pi} \right )dx=\frac{2}{\pi}\int_{0}^{\pi}f(x)\sin\left ( nx \right )dx$$
$$=\frac{2}{\pi}\int_{0}^{\pi}3\sin\left ( nx \right )dx=-\frac{6}{\pi}\left ( \frac{\cos(nx)}{n} \right )\bigg|_{0}^{\pi}=-\frac{6}{n\pi}\left ( \cos(n \pi)-1 \right )$$
Vemos que para $n$ par, $\cos(n\pi)=0$, por lo que:
$$b_{n}=0$$
Para $n$ impar, $\cos(n\pi)=-1$, por lo que:
$$b_{n}=\frac{12}{n\pi}$$
$$\therefore \space \space f(x)=\sum_{n=1}^{\infty}\frac{12}{n\pi}\sin\left ( \frac{2\pi nx}{T} \right )$$
Para $n$ impar.
Tarea moral
Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invito a resolver los siguientes ejercicios propuestos relacionados con el tema visto.
Aproxime las siguientes funciones con serie de Fourier.
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- $f(x)=x^{2}$ en el intervalo $[-2,2]$.
- $f(x)=x^{3}$ en el intervalo $[-1,1]$.
- $f(x)=e^{|x|}$ en el intervalo $[-\pi,\pi]$.
- $f(x)=x\cos(x)$ en el intervalo $[-2,2]$.
- $f(x)=\left\lbrace\begin{array}{c} x+5 \space \space \space si \space \space \space -2\leq x < 0 \\ x-5 \space \space \space si \space \space \space 0 \leq x \leq 2 \end{array}\right.$
Más adelante…
En esta sección vimos las series de Fourier con funciones pares e impares en los cuales se obtienen series cosenoidales y senoidales respectivamente como resultado de las propiedades de las funciones pares e impares, en la siguiente sección veremos la forma exponencial de las series de Fourier.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral II.
- Entrada anterior del curso: Cálculo Diferencial e Integral II: Series de Fourier – El blog de Leo (nekomath.com)
- Siguiente entrada del curso: Cálculo Diferencial e Integral II: Forma exponencial de las series de Fourier – El blog de Leo (nekomath.com)