Introducción

Después de haber revisado la definición de sucesión convergente y haber calculado el límite de varias sucesiones, es momento de probar algunos resultados que nos permitan conocer qué sucede con las operaciones entre sucesiones convergentes. En esta entrada, demostraremos que la suma y el producto de sucesiones convergentes dan lugar a nuevas sucesiones que convergen a la suma y el producto de los límites respectivamente.

Suma de sucesiones convergentes

Daremos inicio con la prueba de que la suma sucesiones convergentes también converge y lo hace a la suma de los límites correspondientes.

Proposición. Sean $\{a_n \}$ y $\{ b_n \}$ dos sucesiones tales que
$$\lim_{n \to \infty} a_n = L \text{ y } \lim_{n \to \infty} b_n = M.$$
Entonces se tiene
$$\lim_{n \to \infty} (a_n + b_n) = L + M.$$

Demostración.

Empleando la definición de sucesión convergente, lo que debemos demostrar es que para todo $\varepsilon > 0$, existe $n_0 \in \mathbb{N}$ tal que para todo $n \geq n_0$ se satisface que $|(a_n + b_n) – (L + M) |< \varepsilon$.

Iniciamos la prueba dando un valor arbitrario para épsilon. Sea $\varepsilon > 0$.

Notemos que es posible agrupar los términos de tal forma que la expresión quede acotada por $L$ y $M$, como se muestra a continuación:

$$|(a_n + b_n) – (L + M) | = |(a_n – L ) + (b_n – M) | \leq |a_n – L| + |b_n – M|. \tag{1}$$

Además, por hipótesis, ambas sucesiones son convergentes, es decir,
$$\lim_{n \to \infty} a_n = L \text{ y } \lim_{n \to \infty} b_n = M.$$

Por tanto, podemos tomar un valor arbitrario positivo, en este caso consideremos $\frac{\varepsilon}{2} > 0$, de tal forma que para este valor existe $n_1 \in \mathbb{N}$ tal que para todo $n \geq n_1$, se cumple $$|a_n – L | < \frac{\varepsilon}{2}. \tag{2}$$ 

Análogamente, existe $n_2 \in \mathbb{N}$ tal que para todo $n \geq n_2$, se cumple $$|b_n – M | < \frac{\varepsilon}{2}. \tag{3}$$

Consideremos $n_0 = max\{n_1, n_2 \}$. De esta forma, si $n \geq n_0$, se tiene que $n \geq n_1$ y $n \geq n_2$. Por tanto, si $n \geq n_0$, también se cumplen (2) y (3). Entonces

\begin{align*}
|(a_n + b_n) – (L+M)|& \leq |a_n – L| + |b_n – M| \text{, por (1)} \\
& < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} \text{, por (2) y (3)} \\
& = \varepsilon.
\end{align*}

$$\therefore |(a_n + b_n) – (L + M) | < \varepsilon.$$

$$\therefore \lim_{n \to \infty} (a_n + b_n) = L + M.$$

$\square$

A continuación probaremos qué sucede cuando se multiplica una sucesión por un valor real constante.

Proposición. Sea $\{ a_n \}$ una sucesión en $\mathbb{R}$ y $k \in \mathbb{R}$, $k$ fijo, entonces 

$$\lim_{n \to \infty} k \cdot a_n = k \cdot L.$$

Demostración.

Sea $\varepsilon > 0$. Notemos 

$$ |k \cdot a_n – k \cdot L| = |k(a_n – L)| = |k||a_n – L |.$$

Para el caso de $k=0$, la sucesión $\{k \cdot a_n\}$ se convierte en una sucesión constante donde todos sus términos son cero. Así, consideremos $k \neq 0$ y $\frac{\varepsilon}{|k|} > 0 $. Como $$\lim_{n \to \infty} a_n = L,$$ existe $n_0 \in \mathbb{N}$ tal que para todo $n \geq n_0$ se tiene que

\begin{gather*}
& |a_n – L | < \frac{\varepsilon}{|k|}. \\ \\
\Leftrightarrow & |k||a_n – L| < \varepsilon. \\ \\
\therefore & |k \cdot a_n – k \cdot L| = |k||a_n – L | < \varepsilon.
\end{gather*}

$$\therefore |k \cdot a_n – k \cdot L| < \varepsilon.$$

$$\lim_{n \to \infty} k \cdot a_n = k \cdot L.$$

$\square$

Haciendo uso de las dos proposiciones anteriores, podemos probar fácilmente que la diferencia de dos sucesiones convergentes converge a la diferencia de sus límites.

Corolario. Sean $\{a_n \}$ y $\{ b_n \}$ dos sucesiones tales que
$$\lim_{n \to \infty} a_n = L \text{ y } \lim_{n \to \infty} b_n = M.$$
Entonces se tiene
$$\lim_{n \to \infty} (a_n – b_n) = L – M.$$

Demostración.

\begin{align*}
\lim_{n \to \infty} (a_n – b_n) & = \lim_{n \to \infty} (a_n +(- 1 \cdot b_n)) \\
& = \lim_{n \to \infty} a_n +\lim_{n \to \infty} (- 1 \cdot b_n) \\
& = L + (-1 \cdot M) \\
& = L – M.
\end{align*}

$$\therefore \lim_{n \to \infty} (a_n – b_n) = L – M.$$

$\square$

Sucesiones acotadas

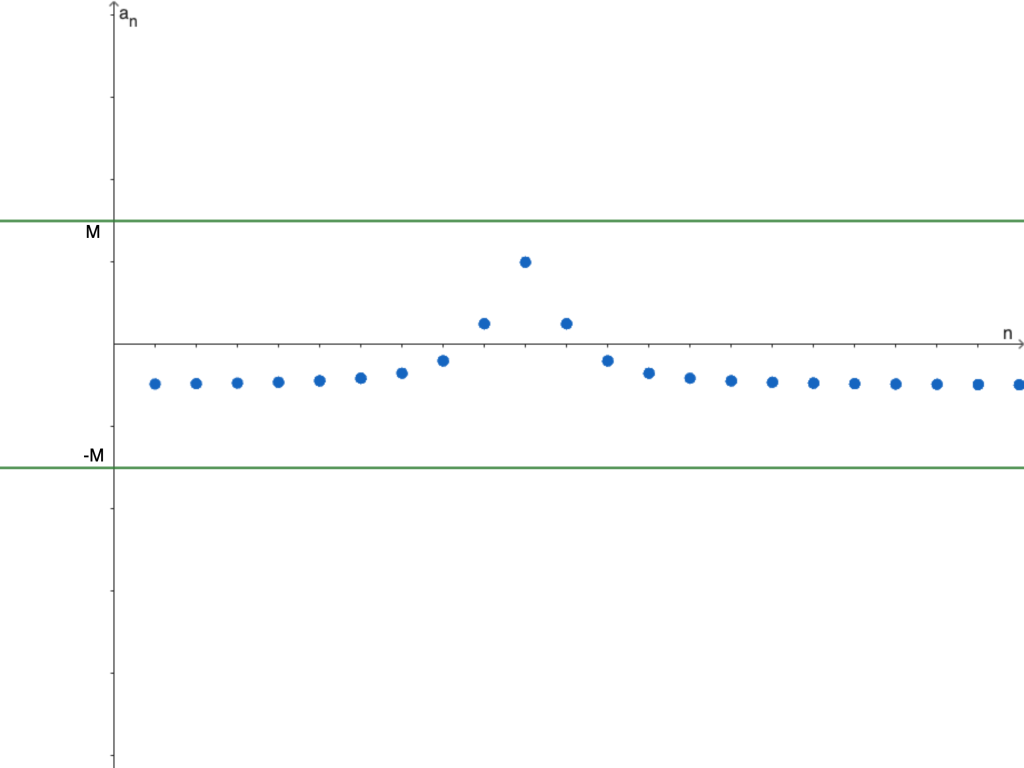
Antes de revisar qué sucede con el producto de sucesiones, estudiaremos el concepto de sucesión acotada, lo que significa que existe un número real $M > 0$ que «encierra» a la sucesión. Es decir, existe un intervalo en el cual todos los términos de la sucesión quedan contenidos. De forma ilustrativa, se muestra la gráfica de la sucesión $\left\lbrace \frac{3}{1+(n-10)^2}-1 \right\rbrace$. De la que más adelante, probaremos su convergencia.

La definición formal se presenta a continuación.

Definición. Se dice que una sucesión $\{a_n \}$ de números reales está acotada si existe un número real $M > 0$ tal que $|a_n| \leq M$ para todo $n \in \mathbb{N}.$

Proposición. Sea $\{ a_n \}$ una sucesión en $\mathbb{R}$. Si $\{ a_n \}$ es convergente, es decir, si existe $L \in \mathbb{R}$ tal que $$\lim_{n \to \infty} a_n = L,$$ entonces $\{ a_n \}$ está acotada. 

Demostración.

Sea $\varepsilon = 1$, como $\{ a_n \}$ converge, entonces existe $n_0 \in \mathbb{N}$ tal que para todo $n \geq n_0$ se tiene que $|a_n – L| < 1$. Además, sabemos que $|a_n| – |L| \leq |a_n – L | < 1$, de lo cual se sigue que

$$|a_n| < 1 + |L| \quad \forall n \geq n_0.$$ 

Notemos que hasta ahora la cota que tenemos es útil únicamente para $n \geq n_0$. Para los primeros $n_0 – 1$ elementos de la sucesión, consideremos $\hat{M} = max \{ |a_1|, |a_2|, …, |a_{n_0-1}| \}$. Así, la cota para toda nuestra sucesión será $M = max \{ \hat{M}, 1 + |L| \}$.

Si $1 \leq n \leq n_0 – 1$, entonces $$|a_n| \leq \hat{M} \leq M \Rightarrow |a_n| \leq M. \tag{1}$$

Por otro lado, si $n \geq n_0$, entonces $$|a_n| \leq 1 + |L| \leq M \Rightarrow |a_n| \leq M. \tag{2}$$

Por (1) y (2), se sigue que para todo $n \in \mathbb{N}$ se tiene que $|a_n| \leq M$. De lo que se concluye que la sucesión $\{a_n\}$ está acotada.

$\square$

Observación. Criterio de no convergencia: Dado que toda sucesión convergente está acotada, entonces, por contrapuesta, si una sucesión no está acotada no puede ser convergente.

Ahora que hemos probado la proposición anterior, podríamos preguntarnos si el regreso es cierto, es decir, ¿toda sucesión acotada converge? La respuesta es no y, de hecho, el contraejemplo lo revisamos en una entrada anterior: $\{ (-1)^n \}$. Se demostró que es una sucesión no convergente y está acotada por $1$.

Producto de sucesiones convergentes

Después de conocer el concepto de sucesión acotado, estamos listos para probar que el producto de sucesiones convergentes converge al producto de sus límites.

Proposición. Sean $\{a_n \}$ y $\{ b_n \}$ dos sucesiones tales que
$$\lim_{n \to \infty} a_n = L \text{ y } \lim_{n \to \infty} b_n = M.$$
Entonces se tiene
$$\lim_{n \to \infty} (a_n \cdot b_n) = L \cdot M.$$

Demostración.

Sea $\varepsilon > 0$.

Con la finalidad de factorizar y obtener expresiones en términos de las sucesiones individuales, sumaremos un cero, $a_nM-a_nM$, a la expresión $|a_n b_n – LM|$.

\begin{align*}
|a_n b_n – LM| & = |a_n b_n – a_n M + a_n M – LM| \\
& \leq |a_n (b_n – M)| + M (a_n – L)| \\
& = |a_n | |b_n – M| + |M| |a_n – L|.
\end{align*}

Además, como $\{a_n\}$ es convergente, entonces está acotada, es decir, existe $J > 0$ tal que para todo $n \in \mathbb{N}$, entonces $|a_n| \leq J$. De la expresión anterior se sigue

\begin{align*}
|a_n b_n – LM| & \leq |a_n | |b_n – M| + |M| |a_n – L| \\
& \leq J|b_n – M| + |M| |a_n – L| \text{, pues } J > 0. \\
\end{align*}

$$\therefore |a_n b_n – LM| \leq J|b_n – M| + |M| |a_n – L|. \tag{1}$$

Consideremos $K = max\{J, |M| \}$. De $(1)$ se sigue que

$$|a_n b_n – LM| \leq K|b_n – M| + K|a_n – L|. \tag{2}$$

Consideremos $\frac{\varepsilon}{2K} > 0$.

\begin{gather*}
\text{Como } \lim_{n \to \infty} a_n = L \text{, existe } n_1 \in \mathbb{N}, \text{ tal que } \forall n \geq n_1, |a_n-L| < \frac{\varepsilon}{2K}. \\

\text{Como } \lim_{n \to \infty} b_n = M \text{, existe } n_2 \in \mathbb{N}, \text{ tal que } \forall n \geq n_2, |b_n-L| < \frac{\varepsilon}{2K}.
\end{gather*}

Tomemos $n_0 = max\{n_1, n_2\}$. Si $n \geq n_0$, entonces $n \geq n_1$, $n \geq n_2$ y junto con $(2)$ se sigue que

\begin{align*}
|a_n b_n – LM| & \leq K|b_n – M| + K|a_n – L| \\
& < K \left( \frac{\varepsilon}{2K} \right) + K \left( \frac{\varepsilon}{2K} \right) \\
& = \varepsilon.
\end{align*}

$$\therefore |a_n b_n – LM| < \varepsilon.$$

$$\therefore \lim_{n \to \infty} (a_n \cdot b_n) = L \cdot M.$$

$\square$

A continuación, revisaremos un par de ejemplos donde se usan las propiedades que se demostraron en la entrada.

Ejemplo 1. Encuentra el siguiente límite $$\lim_{n \to \infty} -\frac{3}{n^2} + 1.$$

En la entrada anterior, probamos que $$\lim_{n \to \infty} \frac{1}{n} = 0.$$

Además, $$- \frac{3}{n^2}+1 = -3 \cdot \frac{1}{n} \cdot \frac{1}{n} + 1.$$

Empleando la expresión anterior y haciendo uso de las propiedades demostradas, tenemos

\begin{align*}
\lim_{n \to \infty} -\frac{3}{n^2} + 1 & = \lim_{n \to \infty} -3 \cdot \frac{1}{n} \cdot \frac{1}{n} + 1\\
& = -3 \cdot 0 \cdot 0 + 1\\
& = 1.
\end{align*}

$$\therefore \lim_{n \to \infty} -\frac{3}{n^2} + 1 = 1.$$

Ejemplo 2. Encuentra el siguiente límite $$\lim_{n \to \infty} 2n-2\sqrt{n^2+n}+1.$$

Factorizando la expresión anterior, obtenemos que
\begin{align*}
2n-2\sqrt{n^2+n}+1 & = (n+1) – 2 \sqrt{n}\sqrt{n+1}+ n \\
&= \left( \sqrt{n+1}-\sqrt{n}\right)^2 \\
& = \left( \sqrt{n+1}-\sqrt{n}\right) \left( \sqrt{n+1}-\sqrt{n}\right).
\end{align*}

En la entrada anterior, probamos que $$\lim_{n \to \infty} \left( \sqrt{n+1}-\sqrt{n}\right) = 0.$$

De esta forma, se tiene que

\begin{align*}
\lim_{n \to \infty} 2n-2\sqrt{n^2+n}+1 & = \lim_{n \to \infty} \left( \sqrt{n+1}-\sqrt{n}\right) \left( \sqrt{n+1}-\sqrt{n}\right) \\
& = 0 \cdot 0 \\
& = 0.
\end{align*}

$$\therefore \lim_{n \to \infty} 2n-2\sqrt{n^2+n}+1 = 0.$$

Más adelante…

En la siguiente entrada revisaremos el caso de la división entre sucesiones convergentes. Complementaremos nuestro estudio revisando una categoría especial de sucesiones llamadas monótonas, y probaremos diversas propiedades de las mismas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

• Prueba que si $\{a_n \}$ y $\{b_n \}$ son dos sucesiones tales $\{ a_n \}$ y $\{a_n+b_n\}$ convergen, entonces $\{b_n \}$ también converge.
• Prueba que si $\{a_n \}$ y $\{b_n \}$ son dos sucesiones tales $\{ a_n \}$ converge a $L \neq 0$ y $\{a_n \cdot b_n\}$ converge, entonces $\{b_n \}$ también converge.
• Usando las proposiciones demostradas en esta entrada, encuentra el límite de las siguientes sucesiones:
  • $\{ c \cdot \frac{1}{n} \}$, con $c \in \mathbb{R}.$
  • $\{ \frac{10}{n} – 7\}.$
  • $\{ \frac{2n^2-n}{n^2} \cdot \left( \frac{10}{n} – 7 \right) \}.$

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral I.
• Entrada anterior del curso: Sucesiones convergentes
• Siguiente entrada del curso: Sucesiones monótonas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»