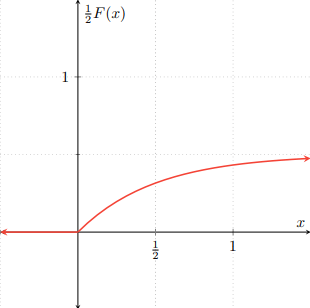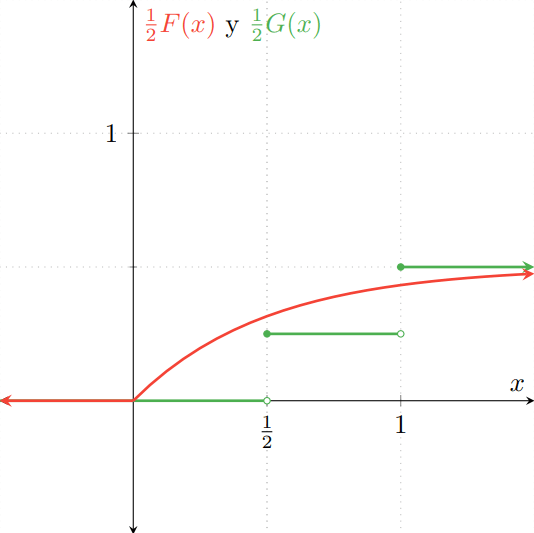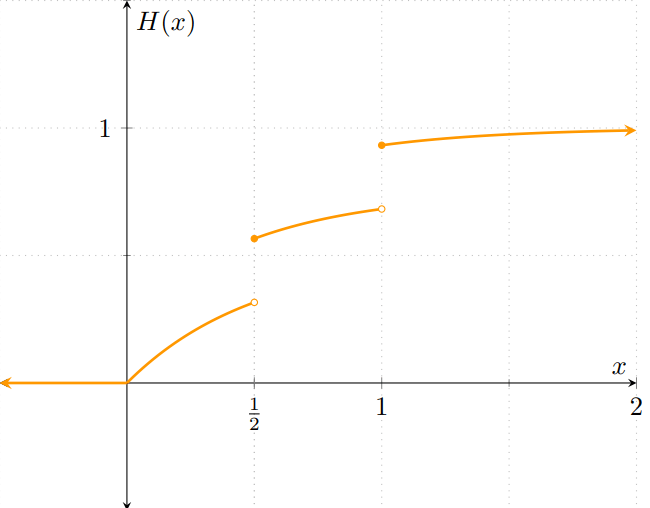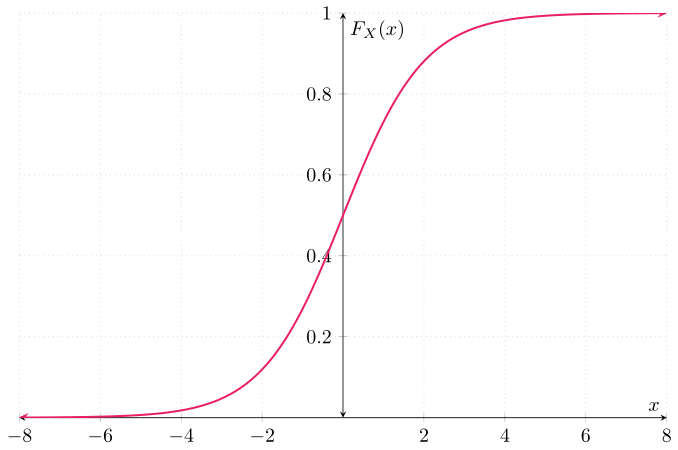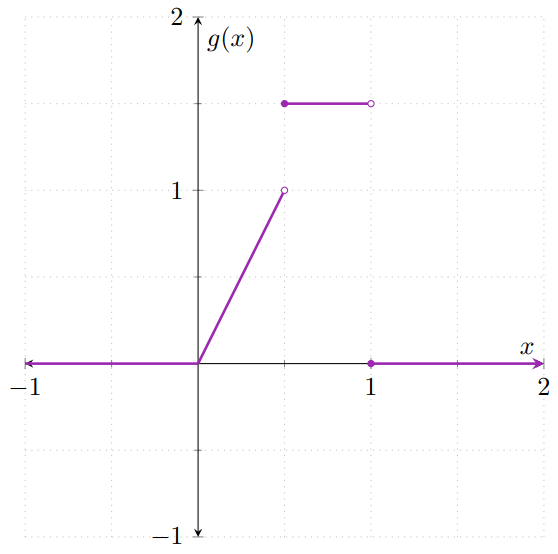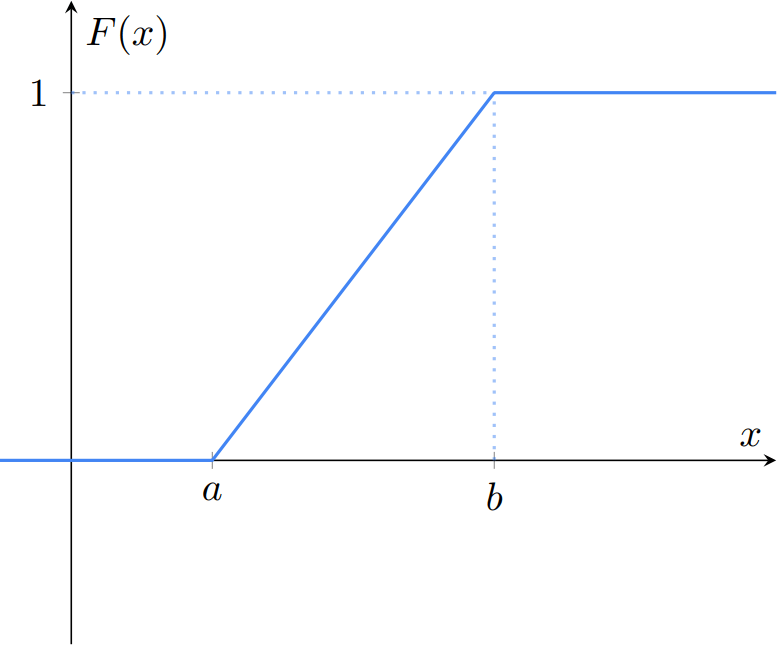Archivo de la etiqueta: Probabilidad I

Probabilidad I: Variables Aleatorias Mixtas

Por Octavio Daniel Ríos García

Introducción

En las últimas entradas presentamos dos tipos muy importantes de v.a.’s que estudiaremos a lo largo del curso. No obstante, estos no son los únicos dos tipos de v.a.’s que existen, hay algunos tipos más. En particular, en esta entrada centraremos nuestra atención en las variables aleatorias mixtas. Estas son v.a.’s que no son ni discretas ni continuas, pero combinan propiedades de ambos tipos. Es decir, una v.a. mixta consta de una parte discreta y de una parte continua, que es la razón por la que reciben el nombre de mixta. Debido a que ya hemos estudiado ambos tipos de v.a.’s, podremos utilizar lo que hemos visto hasta ahora para describir a este nuevo tipo de v.a.’s.

Distribución mixta

Para comenzar, podemos ver una propiedad que ocurre al combinar dos funciones de distribución. Sean $F\colon\RR\to\RR$ y $G\colon\RR\to\RR$ dos funciones de distribución, y sea $\lambda\in[0,1]$. Definimos $H\colon\RR\to\RR$ como sigue:

\[ H(x) = \lambda F(x) + (1 − \lambda) G(x), \qquad \text{para cada $x \in \RR$.} \]

Es decir, para cada $x \in \RR$, $H(x)$ es una combinación lineal de $F(x)$ y $G(x)$. Más aún, como $\lambda$ es algún valor en $[0,1]$, se trata de una combinación convexa. Bien, ¡pues resulta que $H$ es una función de distribución! Te dejamos la comprobación de este hecho como tarea moral.

En particular, cuando $F$ y $G$ son funciones de distribución discretas, $H$ también es una función de distribución discreta. En cambio, cuando $F$ y $G$ son funciones de distribución absolutamente continuas, $H$ también es absolutamente continua.

Por otro lado, el tema principal de esta entrada surge cuando una de las dos distribuciones es discreta y la otra es continua. En tal caso, $H$ no es discreta ni continua, y es llamada una función de distribución mixta.

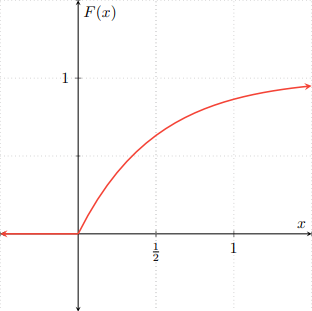
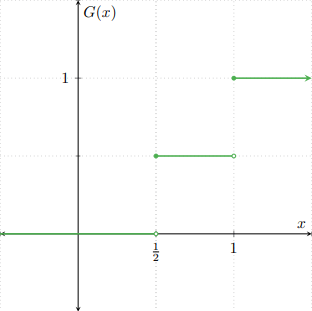
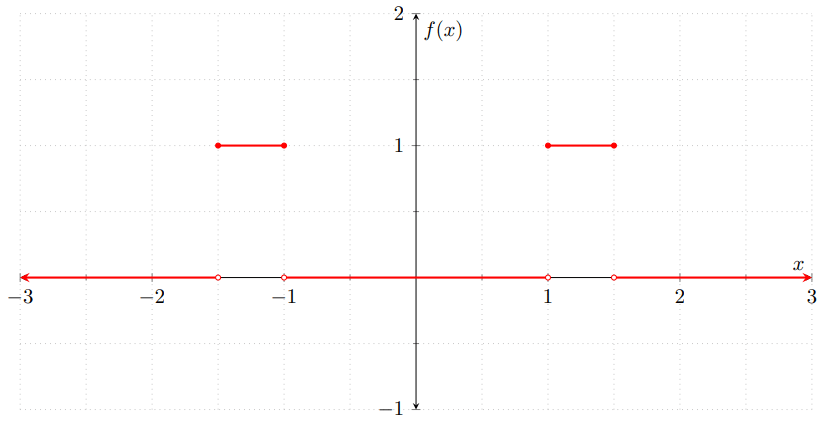
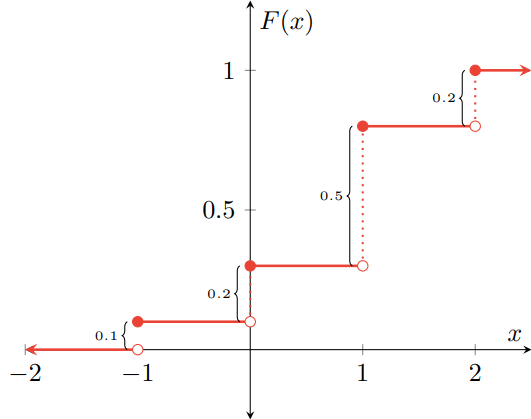
Ejemplo. Sean $F\colon\RR\to\RR$ y $G\colon\RR\to\RR$ las siguientes funciones de distribución.

\begin{align*}F(x) &= \begin{cases} 1 − e^{−2x} & \text{si $x \geq 0$,} \\[1em] 0 & \text{en otro caso,} \end{cases} & G(x) &= \begin{cases} 0 & \text{si $x < \frac{1}{2}$,} \\[1em] \dfrac{1}{2} & \text{si $\frac{1}{2} \leq x < 1$,} \\[1em] 1 & \text{si $x \geq 1$.}\end{cases} \end{align*}

Gráficamente, $F$ y $G$ se ven como sigue.

Definimos $H\colon\RR\to\RR$ como sigue.

\[ H(x) = \frac{1}{2}F(x) + \frac{1}{2}G(x) \qquad \text{para cada $x \in \RR$.} \]

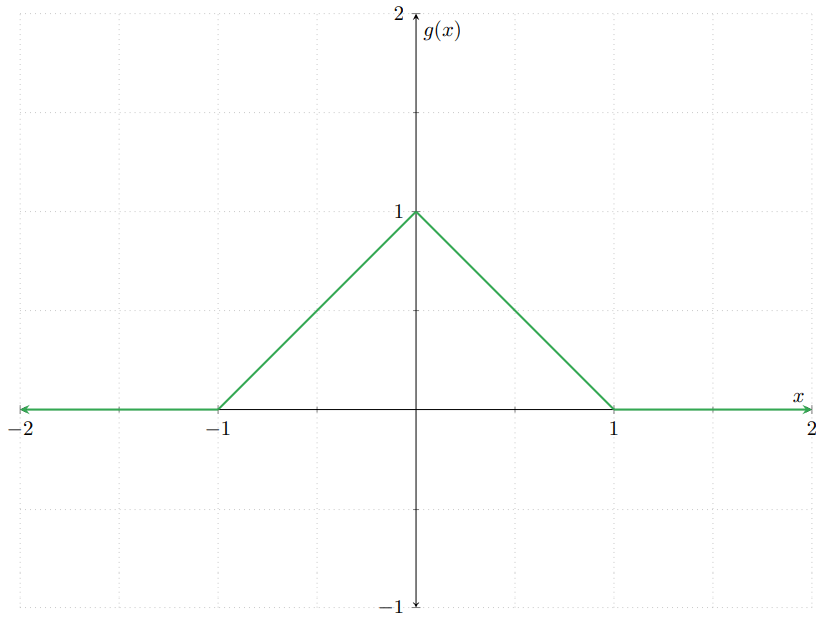
Para visualizar un poco cómo se obtiene la gráfica de $H$, primero hay que multiplicar a $F$ y a $G$ por $\frac{1}{2}$, que nos da las siguientes gráficas:

Observa que se parecen mucho a las gráficas de las distribuciones $F$ y $G$, pero «aplastadas». El «aplastamiento» corresponde a que se han multiplicado por $\frac{1}{2}$. Al superponer ambas gráficas, obtenemos la siguiente figura:

Y en la gráfica de $H$, en el eje vertical tomará los valores $\frac{1}{2}F(x) + \frac{1}{2}G(x)$ para cada $x \in \RR$. La gráfica resultante es la siguiente:

Observa cómo la gráfica de $H$ es diferente a las que hemos visto en las últimas entradas: no es la función de distribución de una v.a. discreta porque no es una función escalonada, pero tampoco es la distribución de una v.a. continua porque presenta discontinuidades.

Sin embargo, ¡sí es una función de distribución! Es no-decreciente, continua por la derecha y sus límites a $-\infty$ e $\infty$ son $0$ y $1$, respectivamente. Por ello, sí es la función de distribución de alguna v.a… aún cuando esa v.a. no sea ni discreta ni continua.

De manera explícita, $H\colon\RR\to\RR$ es la función

\[ H(x) = \begin{cases} 0 & \text{si $x < 0$}, \\[1em] \dfrac{1 − e^{−2x}}{2} & \text{si $0 \leq x < \frac{1}{2}$}, \\[1em] \dfrac{1}{4} + \dfrac{1 − e^{−2x}}{2} & \text{si $\frac{1}{2} \leq x < 1$}, \\[1em] \dfrac{1}{2} + \dfrac{1 − e^{−2x}}{2} & \text{si $x \geq 1$}, \end{cases} \]

Sea $X$ una v.a. aleatoria con distribución $H$. Es decir, $X$ es una v.a. cuya función de distribución es $H$. Hay algunos aspectos interesantes que tiene una v.a. con esta distribución. Primero, los puntos de discontinuidad de $H$ son aquellos puntos con masa de probabilidad mayor a $0$. Observa que

\[ \Prob{X = \frac{1}{2}} = H{\left(\frac{1}{2}\right)} − H{\left(\frac{1}{2}−\right)} \]

Ahora, hay que tener cuidado con $H{\left(\frac{1}{2}−\right)}$. Para obtener este valor, hay que ver cómo se comporta $H(x)$ cuando $x \to \frac{1}{2}$ por la izquierda. Como $x$ se acerca por la izquierda a $\frac{1}{2}$, necesariamente el valor de $x$ es menor a $\frac{1}{2}$, así que $H(x) = \dfrac{1 − e^{−2x}}{2}$. Así, tenemos que

\[ H{\left(\frac{1}{2}−\right)} = \lim_{x\to{\frac{1}{2}}^{-}} H(x) = \lim_{x\to{\frac{1}{2}}^{-}} \dfrac{1 − e^{−2x}}{2} = \dfrac{1 − e^{−2{\left( \frac{1}{2} \right)}}}{2} = \dfrac{1 − e^{−1}}{2}. \]

Este límite fue fácil de evaluar porque la expresión de $H$ para $x < \frac{1}{2}$ describe una función continua. Es decir, $H(x)$ se acerca al valor $\dfrac{1 − e^{−1}}{2}$ cuando $x$ se acerca a $\frac{1}{2}$ por la izquierda. Aún cuando $H$ brinca en ese punto, el límite por la izquierda corresponde al lugar donde se encuentra el hoyito en la gráfica.

En consecuencia, tenemos que

\[ \Prob{X = \frac{1}{2}} = \frac{1}{4} + \dfrac{1 − e^{−1}}{2} − {\left(\dfrac{1 − e^{−1}}{2}\right)} = \frac{1}{4}. \]

De manera similar podemos obtener que

\[ \Prob{X = 1} = \frac{1}{2} + \dfrac{1 − e^{−2}}{2} − {\frac{1}{4} + \left(\dfrac{1 − e^{−2}}{2}\right)} = \frac{1}{4}, \]

por lo que hay dos puntos que tienen masa de probabilidad mayor a $0$. Esto es algo que no pasa en las v.a.’s absolutamente continuas. Debido a esto, cuando se trata de v.a.’s mixtas, hay que tener cuidado en el cálculo de probabilidades de algunos eventos. Por ejemplo,

\[ \Prob{X \leq \frac{1}{2}} = H{\left(\frac{1}{2}\right)} = \frac{1}{4} + \dfrac{1 − e^{−1}}{2}, \]

pero por otro lado,

\[ \Prob{X < \frac{1}{2}} = H{\left(\frac{1}{2}\right)} − \Prob{X = \frac{1}{2}} = \frac{1}{4} + \dfrac{1 − e^{−1}}{2} − \frac{1}{4} = \dfrac{1 − e^{−1}}{2}. \]

En consecuencia, existe $a \in \RR$ tal que $\Prob{X \leq a} \neq \Prob{X < a}$, que es algo que pasa en las v.a.’s discretas. Esos puntos son precisamente los puntos en los que la función de distribución presenta una discontinuidad, por lo que hay que tener cuidado cuando una desigualdad involucra a uno de estos puntos. En consecuencia, también se debe de tener cuidado al obtener la probabilidad de intervalos de la forma $(a,b)$, $[a,b]$, $(a,b]$, etcétera, cuando $a$ y $b$ son puntos en los que la distribución presenta una discontinuidad.

Otra manera de obtener variables aleatorias mixtas

Además de hacer combinaciones lineales de funciones de distribución, también es posible obtener v.a.’s mixtas a partir de v.a.’s continuas. Sea $X\colon\Omega\to\RR$ una v.a. continua, y sea $c \in \RR$ una constante tal que $0 < F_{X}(c) < 1$ (esto es, la distribución de $X$ evaluada en $c$ es mayor a $0$ y menor a $1$). Definimos las variables aleatorias $U\colon\Omega\to\RR$ y $L\colon\Omega\to\RR$ como sigue:

\begin{align*} U(\omega) &= \max{\left\lbrace X(\omega), c \right\rbrace} \qquad \text{para cada $\omega \in \Omega$}, \\[1em] L(\omega) &= \min{\left\lbrace X(\omega), c \right\rbrace} \qquad \text{para cada $\omega \in \Omega$}. \end{align*}

Resulta que estas v.a.’s son ejemplos de variables aleatorias mixtas. Veamos que $U$ lo es. Para ello, hay que analizar dos subconjuntos importantes del espacio muestral sobre el que está definida $X$. Estos son:

\begin{align*} A_{1} &= \{ \, \omega \in \Omega \mid X(\omega) \leq c \, \} & A_{2} &= \{ \,\omega \in \Omega \mid X(\omega) > c \, \}\end{align*}

La razón por la que hemos escogido estos conjuntos se basa en el valor que toma $U(\omega)$ dependiendo de si $X(\omega) \leq c$ o $X(\omega) > c$. Cuando $X(\omega) \leq c$, se tiene que

\[ U(\omega) = \max{\left\lbrace X(\omega), c \right\rbrace} = c, \]

al ser $c$ el mayor de los dos valores. En consecuencia, por la manera en que hemos definido a $A_{1}$, para cada $\omega \in A_{1}$ se cumple que $U(\omega) = c$. Esto significa que

\[ \Prob{U = c} = \Prob{A_{1}} = \Prob{\{ \, \omega \in \Omega \mid X(\omega) \leq c \, \}} = \Prob{X \leq c} = F_{X}(c), \]

y como $c$ cumple que $0 < F_{X}(c) < 1$, se tiene que

\[ \Prob{U = c} > 0, \]

por lo que $U$ tiene al menos un punto con masa de probabilidad mayor a cero. Esto nos indica que $U$ al menos cuenta con una parte discreta, algo que $X$ no tenía.

Por otro lado, para $\omega \in\Omega$ tal que $X(\omega) > c$, se tiene que

\[ U(\omega) = \max{\left\lbrace X(\omega), c \right\rbrace} = X(\omega). \]

Por consiguiente, para cada $\omega \in A_{2}$ se tiene que $U(\omega) = X(\omega)$. Ahora, nota que para cada $x \in [c,\infty)$ se cumple que

\[ \{ \, \omega \in \Omega \mid X(\omega) > x \, \} \subseteq A_{2} \]

pues si $\omega \in \Omega$ satisface $X(\omega) > x$, como $x \in [c,\infty)$, se tiene que $x \geq c$, y por lo tanto, $X(\omega) > c$. Luego, $\omega \in A_{2}$. Por tanto, para $x \in [c, \infty)$ se cumple $\Prob{X > x} = \Prob{U > x}$, pues $X(\omega) = U(\omega)$ en cada uno de los $\omega \in (X > x)$. Así, para cada $x \in [c,\infty)$ se tiene que

\begin{align*} \Prob{X > x} = \Prob{U > x} &\iff 1 − \Prob{X \leq x} = 1 − \Prob{U \leq x} \\[1em] &\iff − \Prob{X \leq x} = − \Prob{U \leq x} \\[1em] &\iff \Prob{X \leq x} = \Prob{U \leq x} \\[1em] &\iff F_{X}(x) = F_{U}(x), \end{align*}

es decir, $X$ y $U$ tienen la misma función de distribución sobre conjunto $[c, \infty)$. Esto garantiza que, sobre $[c, \infty)$, la función de distribución de $U$ es una función absolutamente continua. Sin embargo, hay un detalle importante que necesitamos para asegurarnos de que $U$ es una v.a. mixta. Observa que como pedimos que $F_{X}(c) < 1$, se tiene que $0 < 1 − F_{X}(c)$, y como $F_{X}(c) = F_{U}(c)$, esto garantiza que $0 < 1 − F_{U}(c)$. En conclusión, $\Prob{U > c} > 0$, garantizando que $U$ no es una v.a. exclusivamente discreta.

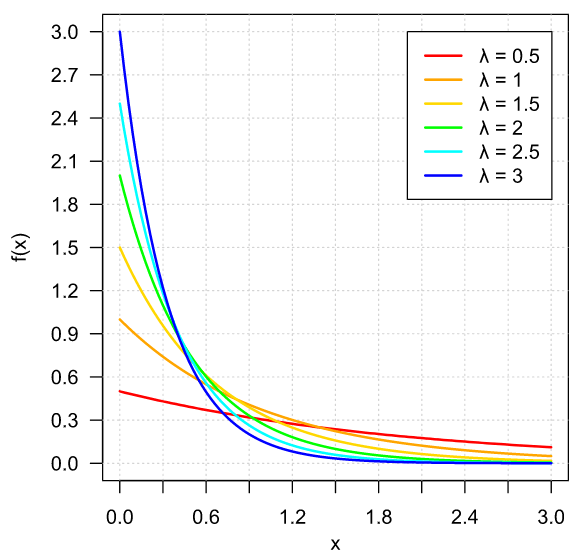
Ejemplo. Sea $X\colon\Omega\to\RR$ una v.a. con función de densidad $f_{X}\colon\RR\to\RR$ dada por

\begin{align*} f_{X}(x) &= \frac{e^{-x}}{(1 + e^{-x})^{2}} & \text{para cada $x \in \RR$}, \end{align*}

y sea $U\colon\Omega\to\RR$ la v.a. dada por

\begin{align*} U(\omega) &= \max{\left\lbrace X(\omega), 0 \right\rbrace} & \text{para cada $\omega \in \Omega$}. \end{align*}

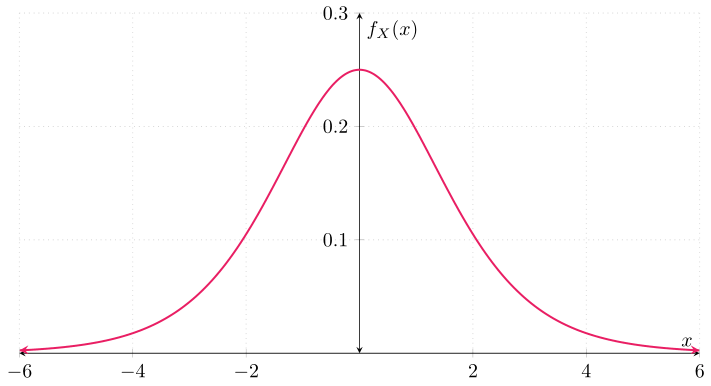
Cuando una v.a. tiene esta función de densidad, se dice que sigue una distribución logística. Ahora, ¿cuál es la función de distribución de $U$? Para obtenerla, primero obtengamos la función de distribución de $X$, $F_{X}$. Conocemos la función de densidad de $X$. Gráficamente:

**Figura.** Gráfica de la función de **densidad** de $X$.

Así que podemos obtener la distribución de $X$ a partir de esta. Así, para cada $x \in \RR$ tenemos que

\begin{align} \label{eq:dist1} F_{X}(x) = \int_{-\infty}^{x} f_{X}(t) \,\mathrm{d}t = \int_{-\infty}^{x} \frac{e^{-t}}{(1 + e^{-t})^{2}} \,\mathrm{d}t. \end{align}

Mediante una sustitución de variables, podemos obtener que la primitiva de $f_{X}$ que satisface lo anterior es

\begin{align} \label{eq:dist2} F_{X}(x) &= \frac{1}{1 + e^{-x}} & \text{para cada $x\in\RR$}. \end{align}

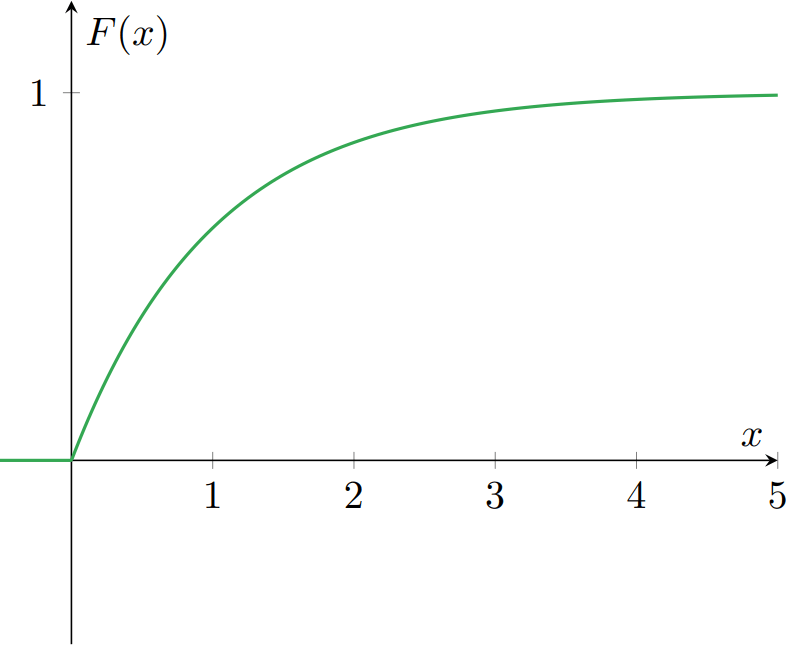
Es decir, esta es la función de distribución de $X$. Gráficamente:

**Figura.** Gráfica de la función de distribución de $X$.

Ahora, para obtener la función de distribución de $U$, hay que ver varios casos. Sea $u \in \RR$ tal que $u < 0$. Para este caso, tenemos que

\[ F_{U}(u) = \Prob{U \leq u} = \Prob{\max\{X, 0\} \leq u}. \]

Sin embargo, como $u < 0$ y $\max\{X, 0\} \geq 0$, el evento $(\max\{X,0\} \leq u) = \emptyset$, pues

\[ (U \leq u) = (\max\{X,0\} \leq u) = \{\, \omega \in \Omega \mid \max\{X(\omega), 0\} \leq u \,\}, \]

y para que exista algún $\omega \in (U \leq u)$, debe de cumplirse que $\max\{X(\omega), 0\} \leq u < 0$, lo cual es imposible. En consecuencia, se tiene que

\begin{align*} F_{U}(u) &= 0 & \text{para $u < 0$}. \end{align*}

Por otro lado, para $u = 0$, tenemos que

\[ F_{U}(u) = \Prob{U \leq 0} = \Prob{U = 0} + \Prob{U < 0} = \Prob{U = 0}. \]

Por su parte, $\Prob{U = 0} = \Prob{\max\{X, 0\} = 0}$, así que hay que recurrir a la distribución de $X$ para obtener este valor. Así,

\begin{align*} \Prob{\max\{X, 0\} = 0} &= \Prob{\{\, \omega \in \Omega \mid \max\{X(\omega), 0\}} = 0 \,\} \\[1em] &= \Prob{\{\, \omega \in \Omega \mid X(\omega) \leq 0 \,\}} \\[1em] &= \Prob{X \leq 0} \\[1em] &= F_{X}(0) \\[1em] &= \frac{1}{1 + e^{-(0)}} \\[1em] &= \frac{1}{1 + 1} \\[1em] &= \frac{1}{2}. \end{align*}

De este modo, $F_{U}(0) = \frac{1}{2}$. Así, tenemos que

\[ F_{U}(u) = \begin{cases} 0 & \text{si $u < 0$}, \\[1em] \frac{1}{2} & \text{si $u = 0$}. \end{cases} \]

Finalmente, para $u > 0$, ya vimos (en el caso general) que

\[ F_{U}(u) = F_{X}(u) = \frac{1}{1 + e^{-u}}\]

por lo que la función de distribución de $U$ queda como

\[ F_{U}(u) = \begin{cases} 0 & \text{si $u < 0$}, \\[1em] \dfrac{1}{2} & \text{si $u = 0$}, \\[1em] \dfrac{1}{1 + e^{-u}} & \text{si $u > 0$}.\end{cases} \]

Gráficamente, la función de distribución de $U$ se ve así:

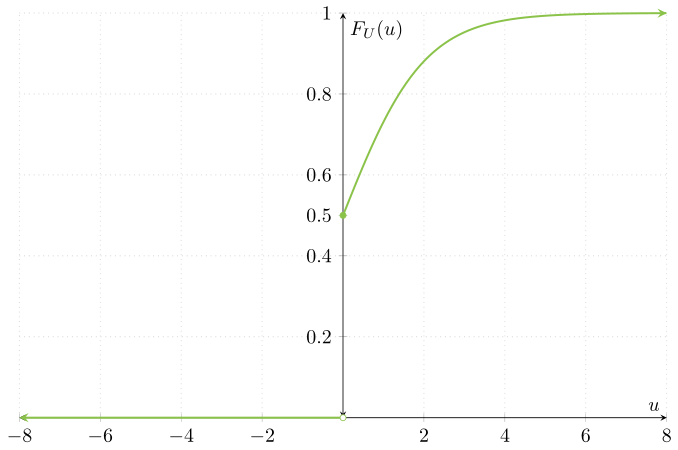
**Figura.** Gráfica de la función de **distribución** de $U$.

Observa que la función de distribución de $U$ es precisamente la de $X$, pero truncada. De hecho, como comentamos previamente, para cada $x \geq 0$ se cumple que $F_{U}(x) = F_{X}(x)$. Sin embargo, la función de distribución de $U$ es $0$ para cada $x<0$, pues $U$ no toma valores menores a $0$.

Tarea moral

Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.

Sean $F\colon\RR\to\RR$ y $G\colon\RR\to\RR$ dos funciones de distribución. Demuestra que para cualquier $\lambda\in [0,1]$, la función $H\colon\RR\to\RR$ dada por\[ H(x) = \lambda F(x) + (1 − \lambda) G(x), \qquad \text{para cada $x \in \RR$,} \]es una función de distribución.
Sean $X\colon\Omega\to\RR$ una v.a. continua y $c \in \RR$ tal que $0 < F_{X}(c) < 1$. Sea $L\colon\Omega\to\RR$ la v.a. dada por\[ L(\omega) = \min{\left\lbrace X(\omega), c \right\rbrace} \qquad \text{para cada $\omega \in \Omega$}. \]Verifica que $L$ es una v.a. mixta.
Al definir las v.a.’s del máximo y el mínimo, ¿qué pasa si $F_{X}(c) = 0$ o $F_{X}(c) = 1$? Por ejemplo, toma $X$ una v.a. con distribución exponencial (vista en la entrada pasada), y toma $c = -5$. ¿Qué pasa con las v.a.’s $U = \max{\{ X, c \}}$ y con $L = \min{\{X, c \}}$?
Verifica que la función de distribución dada por \eqref{eq:dist2} es la función que satisface la ecuación \eqref{eq:dist1}.

Más adelante…

Las v.a.’s aleatorias mixtas llegan a hacerse presentes en algunas aplicaciones financieras y estadísticas. En el análisis de supervivencia (correspondiente a la materia de Estadística III, o Modelos de Supervivencia y Series de Tiempo) hay modelos que hacen uso de transformaciones de v.a.’s como el mínimo, dando como resultado v.a.’s mixtas.

Existe un tipo adicional de v.a.’s que no hemos mencionado hasta el momento, que son las variables aleatorias singulares. Cerca del final del curso haremos una mención a este último tipo de v.a.’s, cuando hayamos definido la noción de «convergencia en distribución». Con ello, presentaremos el bosquejo de un ejemplo de una v.a. cuya distribución es singular.

En la siguiente entrada abordaremos el tema de obtener la distribución de funciones de v.a.’s aleatorias, que no será otra cosa que hacer una composición de funciones.

Entradas relacionadas

Ir a Probabilidad I
Entrada anterior del curso: Variables Aleatorias Continuas
Siguiente entrada del curso: Transformaciones de Variables Aleatorias

Probabilidad I: Variables Aleatorias Continuas

Por Octavio Daniel Ríos García

Deja un comentario

Introducción

En la entrada anterior comenzamos el estudio de los dos tipos de v.a.’s que nos interesan, y vimos el caso de las v.a.’s discretas. Sin embargo, puede que te preguntes exactamente por qué es necesaria esta distinción. Por ello, en esta entrada presentaremos las propiedades de las v.a.’s continuas para que compares ambos tipos, y puedas apreciar sus diferencias.

A diferencia de las v.a.’s discretas, las v.a.’s continuas pueden tomar una cantidad infinita no numerable de valores distintos. Es decir, el conjunto de valores que puede tomar una v.a. continua tiene la misma cardinalidad que los números reales.

Definición de una v.a. continua

En la introducción comentamos que las v.a.’s continuas, a grandes rasgos, son aquellas cuyo conjunto de valores posibles es infinito no numerable. Sin embargo, no las definiremos a partir de este hecho, sino a partir de una propiedad que debe cumplir su función de distribución.

Definición. Una variable aleatoria $X$ es absolutamente continua si y sólamente si existe una función $f\colon\RR\to\RR$ integrable y no-negativa tal que para cada $x \in \RR$ se cumple que

\[ F_{X}(x) = \int_{-\infty}^{x} f(t) \text{d}t. \]

Llamamos a $f$ la función de densidad (o simplemente la densidad) de $X$.

A este tipo de v.a.’s se les llama absolutamente continuas debido a que su función de distribución es una función absolutamente continua. Es común encontrarse con el término «continua» en vez de «absolutamente continua«, aunque en contextos más formales existen diferencias entre ambos términos. De manera equivalente, una v.a. $X$ es continua si existe una función $f\colon\RR\to\RR$ integrable y no-negativa tal que para cada $x \in \RR$ se cumple que

\[ \Prob{X \leq x} = \int_{-\infty}^{x} f(t) \text{d}t, \]

por la definición de $F_{X}$. Es decir, $X$ es una v.a. continua si la función de distribución de $X$ puede escribirse como la integral de una función integrable y no-negativa $f$, que es llamada la densidad de $X$. Es decir, las probabilidades de los eventos que involucran a una v.a. continua se pueden expresar en términos del área debajo de su función de densidad.

En consecuencia, si $X$ es una v.a. continua con densidad $f\colon\RR\to\RR$, como $F_{X}(x) \to 1$ cuando $x \to \infty$, se tiene que

\[ \int_{-\infty}^{\infty} f(t)\text{d}t = 1. \]

Además, para cada $a$, $b \in \RR$ tales que $a < b$ se tiene que $\Prob{X \in (a, b]} = F_{X}(b) − F_{X}(a)$, por lo que

\[ \Prob{X \in (a, b]} = \int_{-\infty}^{b} f(t) \text{d}t − \int_{-\infty}^{a} f(t) \text{d}t = \int_{a}^{b} f(t) \text{d}t. \]

Es importante notar que en la definición pedimos que la densidad de una v.a. continua $X$ debe ser una función integrable, lo cual garantiza que la función de distribución de $X$ es continua.

Ejemplo 1. Sea $\lambda \in \RR$ tal que $\lambda > 0$ y sea $X$ una v.a. con distribución $F\colon\RR\to\RR$ dada por

\[ F(x) = \begin{cases} 1 − e^{-\lambda x} & \text{si $x \geq 0$}, \\[1em] 0 & \text{en otro caso.} \end{cases} \]

Gráficamente, para algunos valores de $\lambda$, $F$ se ve como sigue:

**Figura.** Gráfica de la función $F(x) = 1 − e^{-\lambda x}$ para distintos valores de $\lambda$.

Si tomamos a $f\colon\RR\to\RR$ como sigue

\[ f(x) = \begin{cases} \lambda e^{-\lambda x} & \text{si $x \geq 0$}, \\[1em] 0 & \text{en otro caso,} \end{cases} \]

se cumplirá que $f$ es la densidad de $X$. Para verlo, tomamos $x \in \RR$. Primero, observa que si $x < 0$, entonces

\[ \int_{-\infty}^{x} f(t) \mathrm{d}t = \int_{-\infty}^{x} 0 \mathrm{d}t = 0 = F(x), \]

donde $F(x) = 0$ se cumple por la definición de $F$. Por otro lado, para el caso en el que $x \geq 0$ se tiene que

\begin{align*} \int_{-\infty}^{x} f(t) \mathrm{d}t &= \int_{-\infty}^{0} 0 \mathrm{d}t + \int_{0}^{x} \lambda e^{-\lambda t} \mathrm{d}t \\[1em] &= 0 + {\left( − e^{−\lambda t} \right)} \Big|_{0}^{x} \\[1em] &= e^{−\lambda \cdot 0} − e^{−\lambda x} \\[1em] &= 1 − e^{-\lambda x}, \end{align*}

por lo que queda demostrado que para cada $x \in \RR$ se cumple que $F(x) = \int_{−\infty}^{x} f(t) \mathrm{d}t$. Por lo tanto, $f$ es la densidad de $X$.

**Figura.** Gráfica de la función de densidad de $X$, $f(x) = \lambda e^{−\lambda x}$, para algunos valores de $\lambda$.

Cuando una v.a. tiene la función de distribución (y, en consecuencia, la densidad) del ejemplo anterior, se dice que sigue una distribución exponencial. Esta es una de las muchas distribuciones importantes que veremos más adelante.

¿Las v.a.’s continuas tienen función de masa de probabilidad?

Como seguramente ya notaste, la relación que existe entre la densidad y la función de distribución de una v.a. continua se parece mucho a la relación entre la masa de probabilidad y la distribución de una v.a. discreta. En el caso de las discretas, para obtener el valor de $F(x)$ para $x \in \RR$ a partir de la función de masa de probabilidad, lo que se hace es sumar todas las probabilidades de los valores menores o iguales a $x$. Por otro lado, en el caso de las continuas lo que se hace es integrar la función de densidad desde $−\infty$ hasta $x$.

Sin embargo, hay un detalle muy importante en el que difieren las v.a.’s continuas de las discretas, que desarrollaremos a continuación. Sea $X$ una v.a. continua. ¿Recuerdas la siguiente propiedad? La vimos en la entrada pasada. Para cada $a \in \RR$, se cumple que

\[ \Prob{X =a} = F_{X}(a) − F_{X}(a-), \]

donde no olvides que $F_{X}(a-)$ es el límite de $F(x)$ cuando $x$ tiende a $a$ por la izquierda. Sin embargo, en el caso de una v.a. continua, sabemos que existe $f\colon\RR\to\RR$ integrable y no-negativa tal que para cada $x \in \RR$, se cumple que

\[ F_{X}(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t. \]

Debido a que $f$ es una función integrable, la función $F_{X}$ es continua. En particular, es continua por la izquierda, por lo que para cada $a \in \RR$ se cumple que

\[ \Prob{X = a} = F_{X}(a) − F_{X}(a-) = F_{X}(a) − F_{X}(a) = 0. \]

Esto seguramente te resulta confuso, ¿la probabilidad de que la v.a. $X$ tome cualquier valor real es $0$? ¡Así es! Sin embargo, nosotros habíamos dicho que en la probabilidad, medíamos qué tan «probable» es que pase un evento con una calificación del $0$ al $1$. En particular, habíamos acordado que $0$ representa lo más improbable posible. ¿Esto significa que es imposible que una v.a. continua tome algún valor fijo? ¡No! Ten mucho cuidado, nosotros dijimos que cuando un evento tiene probabilidad $0$ esto significa que es lo más improbable posible de acuerdo con la medida de probabilidad que se está utilizando. Esto puede interpretarse como que sí es imposible (como pasa con los puntos de probabilidad $0$ en una v.a. discreta, o los puntos donde la densidad de una v.a. continua vale $0$), o puede significar que es muy improbable, pero no imposible.

Además, debido a esto último, cuando $X$ es una v.a. continua se cumple que

\[ \Prob{X \in (a,b]} = \Prob{X \in (a,b)} = \Prob{X \in [a,b)} = \Prob{X \in [a,b]}, \]

y que

\[ \Prob{X \leq a} = \Prob{X < a}, \qquad \Prob{X \geq a} = \Prob{X > a}, \]

por lo que con las v.a.’s continuas no es necesario preguntarse si la desigualdad es estricta o no. Mucho cuidado, con las discretas sí debes de tener cuidado con eso, porque en las discretas hay valores $a \in \RR$ para los cuales $\Prob{X = a} > 0$.

Pese a que la probabilidad de los eventos $(X = a)$ es $0$ para cada $a \in \RR$ cuando $X$ es una v.a. continua, la variable aleatoria sí puede tomar cualquiera de los valores en los que su función de densidad es mayor a $0$.

Partiendo de una función de densidad

En la entrada pasada vimos que puede definirse la distribución de una v.a. discreta a partir de una función de masa de probabilidad. De manera muy similar, puede definirse la distribución de una v.a. continua a partir de una función de densidad. Sin embargo, hay que establecer las propiedades que debe de satisfacer una función para poder uitlizarla como función de densidad.

Sea $f\colon\RR\to\RR$ una función integrable. Si se cumple que

\begin{align*} f(x) \geq 0 &\quad \text{para cada $x \in \RR$,} \tag{1} \\[1em] \int_{−\infty}^{\infty} f(t) \mathrm{d}t &= 1, \tag{2}\end{align*}

entonces $f$ es la densidad de alguna v.a. continua. Para confirmar este hecho, define $F\colon\RR\to\RR$ como

\[ F(x) = \int_{−\infty}^{x} f(t) \mathrm{d}t, \quad \text{para cada $x \in \RR$,} \]

y demuestra (tarea moral) que $F$ es una función de distribución. Esto es, que $F$ es no-decreciente, continua por la derecha y su límite a $\infty$ es $1$ y a $−\infty$ es $0$.

Ejemplo 2. La función de densidad de una v.a. continua debe de ser integrable. Sin embargo, no tiene por qué ser continua, ya que funciones integrables que tienen discontinuidades. Por ejemplo, considera a $f\colon\RR\to\RR$ dada por

\[ f(x) = \begin{cases} 1 & \text{si $x \in [−1.5, −1]$,} \\[1em] 1 & \text{si $x \in [1, 1.5]$,} \\[1em] 0 & \text{en otro caso.} \end{cases} \]

Gráficamente:

**Figura.** Gráfica de la función $f$. Observa que claramente $f$ **no es una función continua**.

Para ver que $f$ es la función de densidad de alguna v.a. continua, hay que demostrar que $f$ satisface:

\begin{align*} f(x) \geq 0 \quad \text{para cada $x \in \RR$} \qquad \text{y} \qquad \int_{−\infty}^{\infty} f(t) \mathrm{d}t = 1.\end{align*}

Primero, observa que por la definición de $f$, para cada $x \in \RR$ se cumple que $f(x) = 0$ o $f(x) = 1$, por lo que $f$ es no-negativa. Por otro lado, veamos cuánto vale la integral de $f$ sobre $\RR$.

\begin{align*} \int_{−\infty}^{\infty} f(t) \mathrm{d}t &= \int_{−\infty}^{−1.5} f(t) \mathrm{d}t + \int_{−1.5}^{−1} f(t) \mathrm{d}t + \int_{−1}^{1} f(t) \mathrm{d}t + \int_{1}^{1.5} f(t) \mathrm{d}t + \int_{1.5}^{\infty} f(t) \mathrm{d}t \\[1em] &= \int_{−\infty}^{−1.5} 0 \mathrm{d}t + \int_{−1.5}^{−1} 1 \mathrm{d}t + \int_{−1}^{1} 0 \mathrm{d}t + \int_{1}^{1.5} 1 \mathrm{d}t + \int_{1.5}^{\infty} 0 \mathrm{d}t \\[1em] &= \int_{−1.5}^{−1} 1 \mathrm{d}t + \int_{1}^{1.5} 1 \mathrm{d}t \\[1em] &= {\Big( t \, \Big|_{−1.5}^{−1} \Big)} + {\Big( t \, \Big|_{1}^{1.5} \Big)} \\[1em] &= (−1 − (−1.5)) + (1.5 − 1) \\[1em] &= (−1 + 1.5) + (1.5 − 1) \\[1em] &= 0.5 + 0.5 \\[1em] &= 1, \end{align*}

por lo que $\int_{−\infty}^{\infty} f(t) \mathrm{d}t = 1$, así que $f$ es la función de densidad de alguna v.a. continua.

A partir de $f$ podemos obtener la función de distribución que le corresponde, donde para cada $x \in \RR$, se define $F$ como

\[ F(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t. \]

Sin embargo, como $f$ está definida por pedazos, hay que tener cuidado con cada uno de los casos para $x$. En este caso, $f$ tiene $5$ casos que analizar. Primero, cuando $x < -1.5$, tenemos que

\[ F(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t = \int_{-\infty}^{x} 0 \mathrm{d}t = 0, \]

pues $f(x) = 0$ cuando $x < -1.5$. Luego, cuando $-1.5 \leq x \leq 1$, tenemos que

\[ F(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t = \int_{-\infty}^{-1.5} 0 \mathrm{d}t + \int_{-1.5}^{x} 1 \mathrm{d}t = 0 + {\Big( t \, \Big|_{-1.5}^{x} \Big)} = x − (-1.5) = x + 1.5, \]

¡observa con cuidado cómo los integrandos difieren debido a que $f$ está definida por pedazos! Continuando con el ejemplo, cuando $-1 < x < 1$, se tiene que

\begin{align*} F(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t = \int_{-\infty}^{-1.5} 0 \mathrm{d}t + \int_{-1.5}^{-1} 1 \mathrm{d}t + \int_{-1}^{1} 0 \mathrm{d}t &= 0 + {\Big( t \, \Big|_{-1.5}^{-1} \Big)} + 0 \\[1em] &= (-1) − (-1.5) \\[1em] &= 0.5, \end{align*}

es decir, $F$ permanece constante entre $-1$ y $1$, y toma el valor $0.5$. Cuando $1 \leq x \leq 1.5$, la integral queda como sigue

\begin{align*} F(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t &= \int_{-\infty}^{-1.5} 0 \mathrm{d}t + \int_{-1.5}^{-1} 1 \mathrm{d}t + \int_{-1}^{1} 0 \mathrm{d}t + \int_{-1}^{x} 1 \mathrm{d}t \\[1em] &= 0 + {\Big( t \, \Big|_{-1.5}^{-1} \Big)} + 0 + {\Big( t \, \Big|_{1}^{x} \Big)} \\[1em] &= ((-1) − (-1.5)) + (x − 1) \\[1em] &= 0.5 + x − 1 \\[1em] &= x − 0.5, \end{align*}

y así obtenemos la función de distribución asociada a $f$, que es

\[ F(x) = \begin{cases} 0 & \text{si $x < -1.5$}, \\[1em] x + 1.5 & \text{si $-1.5 \leq x \leq 1$}, \\[1em] 0.5 & \text{si $-1 < x < 1$}, \\[1em] x − 0.5 & \text{si $1 \leq x \leq 1.5$}, \\[1em] 1 & \text{si $1.5 \leq x$}, \end{cases} \]

que gráficamente se ve como la siguiente figura

**Figura.** Gráfica de la función de distribución $F$. Observa que, informalmente, puede apreciarse que satisface las propiedades de una función de distribución (como ya lo esperábamos): es no-decreciente, continua por la derecha y sus límites a $-\infty$ e $\infty$ son $0$ y $1$, respectivamente.

Teniendo la función de distribución, es posible calcular muchas probabilidades. Si $U$ es una v.a. cuya distribución es la función $F$ que obtuvimos, entonces podemos obtener:

\[ \Prob{U \leq -\frac{4}{3}} = -\frac{4}{3} + 1.5 = -\frac{4}{3} + \frac{3}{2} = \frac{-8 + 9}{6} = \frac{1}{6} \approx 0.16666, \]

por lo que $\Prob{U \leq -\frac{4}{3}} \approx 16.666\%$. Además, como $U$ es una v.a. continua, se tiene que $\Prob{U \leq -\frac{4}{3}} = \Prob{U < -\frac{4}{3}}$, pues $\Prob{U = -\frac{4}{3}} = 0$. Esto pasa con cualquier valor, como ya mencionamos anteriormente. Por ello, al obtener probabilidades de que una v.a. continua esté dentro de algún intervalo, puedes no preocuparte por los extremos. Otro ejemplo:

\[ \Prob{X \in (-1.2, 1.4]} = F(1.4) − F(-1.2) = (1.4 − 0.5) − ((-1.2) + 1.5) = 0.9 − 0.3 = 0.6, \]

que es igual a $\Prob{X \in (-1.2, 1.4)}$, pues $\Prob{X = 1.4} = 0$.

Recuperando la densidad a partir de la distribución

Habrá situaciones en las que tendremos la función de distribución de una v.a. continua, y necesitaremos su función de densidad. El siguiente ejemplo exhibe una metodología para obtener la densidad de una v.a. continua a partir de su función de distribución.

Ejemplo 3. Sea $Z$ una v.a. con distribución $G\colon\RR\to\RR$ dada por

\[ G(z) = \begin{cases} 0 & \text{si $x < 0$}, \\[1em] z^2 & \text{si $0 \leq z < \frac{1}{2}$}, \\[1em] 1 − \dfrac{3(1 − z)}{2} & \text{si $\frac{1}{2} \leq z < 1$}, \\[1em] 1 & \text{si $z \geq 1$},\end{cases} \]

que gráficamente se ve como sigue:

**Figura.** Gráfica de la función $G$. Parece que sí es una función de distribución… ¡No se te olvide verificarlo!

Ahora, para obtener la función de densidad de $Z$, digamos, $g$. Para hacerlo, hay que hacer el procedimiento inverso al que seguimos en el ejemplo anterior. No obstante, la densidad $g$ será una función definida por pedazos, así como $G$ (y como la densidad del ejemplo anterior).

Además, en lugar de integrar, ahora tenemos que encontrar la derivada $G$. Es decir, la función $g$ que buscamos debe de satisfacer que

\[ G'(z) = g(z), \qquad \text{para cada $z\in\RR$.} \]

Sin embargo, observa que la función no es diferenciable sobre todo su dominio. Gráficamente, tiene un piquito en $z=\frac{1}{2}$, que es un indicador de que la función no es diferenciable en ese punto. Lo mismo pasa en $z=1$.

Sin embargo, es posible obtener la derivada de la función $G$ en los pedazos en los que sí es diferenciable. Podemos trabajar de manera similar a como lo hicimos en el ejemplo anterior, analizando cada uno de los casos que contempla la regla de correspondencia de $G$. De este modo, sea $z < 0$. Queremos encontrar $g_{1}$, una función no-negativa, tal que

\[ G(z) = \int_{-\infty}^{z} g_{1}(t) \mathrm{d}t, \]

y como $z < 0$, $G(z) = 0$, por lo que buscamos $g_{1}$ tal que

\[ \int_{-\infty}^{z} g_{1}(t) \mathrm{d}t = 0, \]

que debe de ser una función constante para que se cumpla que $G'(t) = g_{1}(t)$ para $t < 0$. Además, $g_{1}$ debe de ser no-negativa, pues buscamos que sea parte de una función de densidad, la cual debe de ser no negativa. De este modo, la única función $g_{1}$ que satisface este hecho es la función dada por $g_{1}(t) = 0$, pues es constante y su integral de $-\infty$ a $z$ es $0$, con $z < 0$. De este modo, $g$, la derivada de $G$ que buscamos, cumple que $g(z) = 0$ para cada $z < 0$.

Después, para $z \in [0, \frac{1}{2})$, tenemos que

\[ G(z) = z^{2}, \]

y lo que queremos es encontrar una función $g_{2}$ tal que

\[ G(z) = \int_{-\infty}^{0} g_{1}(t) \mathrm{d}t + \int_{0}^{z} g_{2}(t) \mathrm{d}t, \]

donde $g_{1}$ es la que obtuvimos en el paso anterior (gracias al paso anterior sabemos que la derivada de $G$ que estamos construyendo vale $0$ de $-\infty$ a $0$). Por ello, buscamos $g_{2}$ tal que

\[ z^{2} = \int_{-\infty}^{0} g_{1}(t) \mathrm{d}t + \int_{0}^{z} g_{2}(t) \mathrm{d}t = 0 + \int_{0}^{z} g_{2}(t) \mathrm{d}t = \int_{0}^{z} g_{2}(t) \mathrm{d}t, \]

por lo que $g_{2}$ es la función dada por $g_{2}(t) = 2z$ para cada $z \in [0, \frac{1}{2})$; ya que $\frac{\mathrm{d}}{\mathrm{d}z}{\left( z^{2} \right)} = 2z$.

Ahora, para $z \in [\frac{1}{2}, 1)$, se tiene que

\[ G(z) = 1 − \frac{3(1 − z)}{2}, \]

y ahora buscamos una función $g_{3}$ tal que

\[ G(z) = \int_{-\infty}^{0} g_{1}(t) \mathrm{d}t + \int_{0}^{\frac{1}{2}} g_{2}(t) \mathrm{d}t + \int_{\frac{1}{2}}^{z} g_{3}(t) \mathrm{d}t. \]

Desarrollando el lado derecho de esta última igualdad obtenemos la siguiente expresión

\begin{align*} \int_{-\infty}^{0} g_{1}(t) \mathrm{d}t + \int_{0}^{\frac{1}{2}} g_{2}(t) \mathrm{d}t + \int_{\frac{1}{2}}^{z} g_{3}(t) \mathrm{d}t &= 0 + {\left({\left( \frac{1}{2} \right)}^{2} − 0^{2} \right)} + \int_{\frac{1}{2}}^{z}g_{3}(t) \mathrm{d}t \\[1em] &= \frac{1}{4} + \int_{\frac{1}{2}}^{z}g_{3}(t) \mathrm{d}t, \end{align*}

y, por otro lado, desarrollando el lado izquierdo, obtenemos que

\[ G(z) = 1 − \frac{3(1 − z)}{2} = 1 − \frac{3 − 3z}{2} = \frac{2 − (3 − 3z)}{2} = \frac{3z − 1}{2} \]

por lo que la función $g_{3}$ que buscamos debe de cumplir que

\[ \frac{3z − 1}{2} = \frac{1}{4} + \int_{\frac{1}{2}}^{z}g_{3}(t) \mathrm{d}t, \]

que desarrollando un poco, nos dice que $g_{3}$ debe de satisfascer

\[ \frac{3z}{2} − \frac{3}{4} = \int_{\frac{1}{2}}^{z}g_{3}(t) \mathrm{d}t. \]

Ahora, esto es algo que no se notó mucho en el paso anterior en el que obtuvimos $g_{2}$, pero la expresión de la izquierda incluye las constantes de integración. Esto es de esperarse, pues se trata del teorema fundamental del cálculo.

Bien, ahora observa $\frac{\mathrm{d}}{\mathrm{d}z}{\left( \frac{3z}{2} − \frac{3}{4} \right)} = \frac{3}{2}$; así que $g_{3}(t) = \frac{3}{2}$ es la función que queremos. Más aún, podemos confirmarlo integrando $g_{3}$ de $\frac{1}{2}$ a $z$:

\[ \int_{\frac{1}{2}}^{z} \frac{3}{2} \mathrm{d}t = \frac{3}{2} \int_{\frac{1}{2}}^{z} 1 \mathrm{d}t = \frac{3}{2}{\left( z − \frac{1}{2} \right)} = \frac{3z}{2} − \frac{3}{4}, \]

por lo que $g_{3}(t) = \frac{3}{2}$ es precisamente la función que buscamos.

Finalmente, para $z \geq 1$, tenemos que $G(z) = 1$, por lo que nos queda encontrar $g_{4}$ tal que

\begin{align*} 1 &= \int_{-\infty}^{0} g_{1}(t) \mathrm{d}t + \int_{0}^{\frac{1}{2}} g_{2}(t) \mathrm{d}t + \int_{\frac{1}{2}}^{1} g_{3}(t) \mathrm{d}t + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t, \\[1em] &= \int_{-\infty}^{0} 0 \mathrm{d}t + \int_{0}^{\frac{1}{2}} 2t \mathrm{d}t \mathrm{d}t + \int_{\frac{1}{2}}^{1} \frac{3}{2} \mathrm{d}t + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t \\[1em] &= 0 + \frac{1}{4} + {\left( \frac{3}{2} − \frac{3}{4} \right) } + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t \\[1em] &= \frac{1}{4} + {\left( \frac{6 − 3}{4} \right) } + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t \\[1em] &= \frac{1}{4} + \frac{3}{4} + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t \\[1em] &= 1 + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t \end{align*}

por lo que $g_{4}$ debe de satisfacer que

\[ 1 = 1 + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t, \]

o equivalentemente, que $\int_{1}^{\infty} g_{4}(t) \mathrm{d}t = 0$. Similarmente a $g_{1}$, la única función no-negativa que satisface esto es $g_{4}(z) = 0$, para cada $z \geq 1$. Así, colocando cada una de las funciones que hemos obtenido en el caso que le corresponde, obtenemos que la densidad de $Z$ es la función $g\colon\RR\to\RR$ dada por

\[ g(z) = \begin{cases} 0 & \text{si $x < 0$}, \\[1em] 2z & \text{si $0 \leq z < \frac{1}{2}$}, \\[1em] \frac{3}{2} & \text{si $\frac{1}{2} \leq z < 1$}, \\[1em] 0 & \text{si $z \geq 1$},\end{cases} \]

que gráficamente se ve como sigue:

**Figura.** Gráfica de $g$, la densidad de $Z$. Observa que $g$ no es continua, algo que ya dejamos claro que no es necesario. Sin embargo, $g$ claramente es una función integrable.

Usos de las variables aleatorias continuas

Las v.a.’s continuas tienen una cantidad no-numerable de valores que pueden tomar. Esto se debe a que $\RR$ y muchos de sus subconjuntos son ejemplos de conjuntos infinitos no-numerables. Por ejemplo, los intervalos $[0,1]$, $[0, \infty)$, $(−5, 3]$ son ejemplos de conjuntos con cardinalidad infinita no-numerable. Por ello, las v.a.’s continuas se utilizan en fenómenos cuyo resultado amerita usar la precisión de los números reales.

Un primer ejemplo son los fenómenos en donde el resultado es un valor de tiempo. El tiempo que esperas hasta que llega un autobús a la parada en la que lo tomas; el tiempo que tarda en fallar algún aparato electrónico (el ejemplo clásico es el tiempo que tarda un foco en fundirse); el tiempo de vida que le queda a una persona (espeluznante, pero a los actuarios les interesa debido a los seguros de vida); etcétera. Cuando se habla de tiempos, suelen usarse v.a.’s continuas que tengan a $[0, \infty)$ como soporte para asegurar que el modelo contempla únicamente valores no-negativos. Las v.a.’s con distribución exponencial (que mencionamos en el primer ejemplo de esta entrada) son un ejemplo de este tipo de v.a.’s.

Otro ejemplo donde se usan v.a.’s continuas son los fenómenos financieros. El precio de un activo en un momento dado; la paridad cambiaria entre divisas; el valor que tomará la tasa de interés o de rendimiento en un instrumento financiero (como una anualidad) en el futuro; etcétera. La teoría de los procesos estocásticos es la rama de la probabilidad que se encarga del estudio de fenómenos aleatorios a través del tiempo, y resulta fundamental para el análisis de fenómenos financieros como los que aquí mencionamos.

Tarea moral

Demuestra que si $f\colon\RR\to\RR$ es una función que satisface \begin{align*} f(x) \geq 0 \quad \text{para cada $x \in \RR$} \qquad \text{y} \qquad \int_{−\infty}^{\infty} f(t) \mathrm{d}t = 1,\end{align*}entonces $f$ es la función de densidad de alguna v.a. continua. Sugerencia: Define $F\colon\RR\to\RR$ como sigue: para cada $x \in \RR$, \[ F(x) = \int_{−\infty}^{\infty} f(t) \mathrm{d}t, \]y demuestra que $F$ es una función de distribución.
Demuestra que la función $g\colon\RR\to\RR$ dada por\[ g(x) = \begin{cases} x + 1 & \text{si $x \in [−1,0)$,} \\[1em] 1 − x & \text{si $x \in [0, 1]$,} \\[1em] 0 & \text{en otro caso} \end{cases} \]es la función de densidad de alguna v.a. continua. La gráfica de $g$ puede apreciarse en la siguiente figura:
Verifica que la función $G$ del Ejemplo 3 es una función de distribución.

Más adelante…

Es importante que entiendas las diferencias que existen entre las v.a.’s discretas y las continuas. Repasa esta entrada y la anterior las veces que sea necesario para que no te confundas entre ambas. En la siguiente entrada veremos qué es lo que resulta de aplicarle funciones (transformaciones) a una v.a.

En cuanto a las aplicaciones, verás muchísimas más en materias posteriores, como en las materias de estadística. Por nuestro lado veremos varias distribuciones de probabilidad importantes (como la distribución exponencial) con las que seguramente te encontrarás en ese tipo de materias.

Entradas relacionadas

Ir a Probabilidad I
Entrada anterior del curso: Variables Aleatorias Discretas
Siguiente entrada del curso: Variables Aleatorias Mixtas

Probabilidad I: Variables Aleatorias Discretas

Por Octavio Daniel Ríos García

2 respuestas

Introducción

En las entradas pasadas introdujimos los conceptos de variable aleatoria y función de distribución. Además, al final de la entrada pasada comentamos que las variables aleatorias pueden clasificarse como discretas o continuas, dependiendo de la cardinalidad del conjunto de valores que pueden tomar.

En esta entrada trataremos el caso de las variables aleatorias discretas. En el contexto de las matemáticas se usa el término «discreta» para hacer referencia a conjuntos finitos o infinitos numerables. Por ello, a grandes rasgos, las variables aleatorias discretas son aquellas cuyo conjunto de valores que pueden tomar es a lo más infinito numerable.

¡IMPORTANTE! Algunas convenciones que usaremos

De ahora en adelante, escribiremos «variable aleatoria» simplemente como v.a. De este modo, por ejemplo, cuando digamos «sea $X$ una v.a.», deberás de leerlo como «sea $X$ una variable aleatoria».

Por otro lado, usaremos los límites laterales (por la derecha y por la izquierda) de la función de distribución, por lo que introduciremos la siguiente notación: si $F\colon\RR\to\RR$ es una función, entonces

\begin{align*}F(a+) &:= \lim_{x\to a^{+}} F(x), \\ F(a-) &:= \lim_{x\to a^{-}} F(x). \end{align*}

En otras palabras,

$F(a+)$ es el límite de $F(x)$ cuando $x$ tiende a $a$ por la derecha.
$F(a-)$ es el límite de $F(x)$ cuando $x$ tiende a $a$ por la izquierda.

Esta convención facilita la escritura de las fórmulas que involucran a estos límites.

Definición de variable aleatoria discreta

Como su nombre lo indica, una v.a. discreta es aquella v.a. cuyo conjunto de valores que puede tomar es un conjunto de cardinalidad a lo más numerable. Es decir, que la cantidad de valores distintos que puede tomar la v.a. es finito, o infinito numerable.

Definición. Sea $X$ una v.a. sobre $(\Omega, \mathscr{F}, \mathbb{P})$. Diremos que $X$ es una variable aleatoria discreta si el conjunto de valores que puede tomar $X$ es finito o infinito numerable.

De manera más formal, un conjunto $S \in \mathscr{B}(\RR)$ es llamado un soporte de la v.a. $X$ si $\Prob{X \in S} = 1$. Así, $X$ es una v.a. discreta si tiene un soporte finito o infinito numerable.

Cuando $X$ es una v.a. discreta, y el conjunto de valores que toma $X$ es $\{ x_{n} \}_{n\in\mathbb{N}^{+}}$ de tal manera que $x_{n} < x_{n+1}$ para cada $n \in \mathbb{N}^{+}$, la función de distribución de $X$, $F_{X}$, es una función escalonada con una discontinuidad de magnitud $\Prob{X = x_{n}}$ en cada $x_{n}$. Además, $F_{X}$ es constante entre los $x_{n}$, y toma el valor mayor en cada discontinuidad. Esto es algo que puedes observar en el ejemplo 4 de la entrada anterior.

Además, si $X$ es una variable aleatoria cualquiera, se cumple que

\[ \Prob{X = a} = \Prob{X \leq a} − \Prob{X < a} = F_{X}(a) − F_{X}(a-). \]

En particular, cuando $X$ es una variable aleatoria discreta, $\Prob{X = a} > 0$ cuando $a$ es alguno de los valores que puede tomar $X$; y es $0$ en cualquier otro caso. La demostración de que $F_{X}(a-) = \Prob{X < a}$ te la dejamos como parte de la tarea moral.

Más aún, como vimos que la función de distribución de una v.a. contiene toda la información sobre una v.a. $X$, entonces si $X$ es una v.a. discreta, los valores $\Prob{X = a}$ para cada $a \in \RR$ capturan toda la información sobre el comportamiento probabilístico de $X$. ¡Cuidado! Esto sólamente pasa con las v.a.’s discretas, veremos que con las continuas no es así.

Función de masa de probabilidad de una v.a. discreta

A la función que manda a cada $a\in\RR$ al valor $\Prob{X=a}$ se le conoce como la función de masa de probabilidad (en inglés, probability mass function), que definimos a continuación.

Definición. Sea $X$ una v.a. discreta que toma los valores $\{ x_{n} \}_{n\in\mathbb{N}^{+}}$. Se define la función de masa de probabilidad (f.m.p.) de $X$, denotada por $p_{X}\colon\RR\to\RR$, como sigue.

\[ p_{X}(x) = \Prob{X = x}. \]

Esta función también es conocida simplemente como función de probabilidad.

Observa que $p_{X}(x) > 0$ cuando $x$ es alguno de los valores en $\{ x_{n} \}_{n\in\mathbb{N}^{+}}$; y $p_{X}(x) = 0$ en cualquier otro caso. De acuerdo con lo anterior, para cualquier $A \in \mathscr{B}(\RR)$ se tendrá que

\[ \Prob{X \in A} = \sum_{x\in A} p_{X}(x). \]

La suma anterior es discreta, pues $p_{X}(x)$ es mayor a $0$ en a lo más en una cantidad numerable de valores.

Ejemplo 1. Sea $X$ una v.a. con distribución $F\colon\RR\to\RR$ dada por

\[ F(x) = \begin{cases} 0 & \text{si $x < -1$,} \\[1em] 0.1 & \text{si $-1 \leq x < 0$,} \\[1em] 0.3 & \text{si $0 \leq x < 1$,} \\[1em] 0.8 & \text{si $1 \leq x < 2$,} \\[1em] 1 & \text{si $2 \leq x$.}\end{cases} \]

Es decir, la función de distribución de $X$ es $F$. Gráficamente, la función $F$ se ve como sigue:

Los puntos en los que $F$ presenta una discontinuidad son los valores que toma la variable aleatoria $X$, y la magnitud de los saltos es la probabilidad de que tome cada respectivo valor. La magnitud del salto corresponde precisamente a

\[ \Prob{X = a} = F(a) − F(a-), \]

pues en aquellos valores de $a$ en los que hay una discontinuidad, $F(a)$ y $F(a-)$ son valores distintos. Además, observa que para cada $a \in \RR$, $F(a)$ es la probabilidad acumulada por todos los valores menores o iguales a $a$. Por ejemplo, $F(-2) = 0$, que significa que $F$ no ha acumulado probabilidad hasta el valor $-2$. Es decir, todos los números reales menores o iguales a $-2$ acumulan $0$ de probabilidad. Por otro lado, $F(0) = 0.3$, por lo que la probabilidad acumulada hasta $0$ es de $0.3$. Esto es, los números reales que son menores o iguales a $0$ acumulan $0.3$ de la probabilidad.

A partir de la distribución $F$ podemos obtener la función de masa de probabilidad de $X$. Para ello, tenemos que usar la fórmula

\[ \Prob{X = a} = F(a) − F(a-). \]

Esta expresión es distinta de $0$ en todos los valores de $a$ en los que $F$ presenta una discontinuidad, y es $0$ en otro caso. En los puntos de discontinuidad se tiene que:

\begin{array}{lclclcl} \Prob{X =-1} &= & F(-1) − F((-1)-) & = & 0.1 − 0 & = & 0.1, \\
\Prob{X = 0} &= & F(0) − F(0-) & = & 0.3 − 0.1 & = & 0.2, \\
\Prob{X = 1} &= & F(1) − F(1-) & = & 0.8 − 0.3 & = & 0.5, \\ \Prob{X = 2} &= & F(2) − F(2-) & = & 1 − 0.8 & = & 0.2. \\ \end{array}

De este modo, la función de masa de probabilidad de $X$ es la función $p_{X}\colon\RR\to\RR$ dada por

\[ p_{X}(x) = \begin{cases} 0.1 & \text{si $x = -1$,} \\[1em] 0.2 & \text{si $x = 0$ o $x = 2$,} \\[1em] 0.5 & \text{si $x = 1$,} \\[1em] 0 & \text{en otro caso.} \end{cases} \]

Esto significa que la variable aleatoria $X$ toma valores en el conjunto $\{ -1, 0, 1, 2 \}$, que son precisamente los puntos en los que $F$ tiene una discontinuidad.

Conexión entre la función de masa de probabilidad y la función de distribución

En el ejemplo anterior puede observarse que la función de masa de probabilidad de $X$ contiene toda la información sobre el comportamiento probabilístico de $X$, pues gracias a ella podemos saber:

El conjunto de valores que puede tomar $X$, que son aquellos cuya probabilidad es mayor a $0$.
La probabilidad de que tome cada uno de estos valores.

Además, es posible recuperar la función de distribución de $X$ en cada $x \in \RR$ sumando los valores que toma $p_{X}$ hasta $x$.

\[ F(x) = \sum_{y \in (-\infty, x]} p_{X}(y). \]

La suma anterior tendrá a lo más una cantidad numerable de términos, pues $p_{X}(y) > 0$ en a lo más una cantidad numerable de valores. Además, como la función de masa de probabilidad permite recuperar una función de distribución, es suficiente con tener la f.m.p. para conocer el comportamiento probabilístico de una v.a. discreta. Por ello, usualmente en los ejercicios se te dará la función de masa de probabilidad.

Ejemplo 2. Una variable aleatoria que toma una cantidad infinita numerable de valores también es discreta. Por ejemplo, sea $Y$ una v.a. con función de masa de probabilidad $p_{Y}\colon\RR\to\RR$ dada por

\[ p_{Y}(y) = \begin{cases} \dfrac{1}{2^{y}} & \text{si $y \in \mathbb{N}^{+}$,} \\[1em] 0 & \text{en otro caso.} \end{cases} \]

De este modo, tenemos que

\begin{align*} p_{Y}(1) = \Prob{Y = 1} = \frac{1}{2^{1}} = \frac{1}{2}, \\[1em] p_{Y}(2) = \Prob{Y = 2} = \frac{1}{2^{2}} = \frac{1}{4}, \\[1em] p_{Y}(3) = \Prob{Y = 3} = \frac{1}{2^{3}} = \frac{1}{8}, \end{align*}

etcétera. Sin embargo, observa que ahora te estamos dando una función de masa de probabilidad, y no te damos una función de distribución. ¿Cómo podemos estar seguros de que la función que nos están dando representa el comportamiento probabilístico de manera correcta? Hay dos cosas de tenemos que revisar:

Para cada $y \in \RR$, se debe de cumplir que $p_{Y}(y) \geq 0$. Recuerda, $p_{Y}(y)$ es una probabilidad, así que debe de ser mayor o igual a $0$.
Que la suma de todos los valores que toma $p_{Y}$ es $1$. Esto debe de pasar porque la probabilidad de que $Y$ tome alguno de los valores que puede tomar debe de ser $1$.

La primera propiedad se cumple, pues $p_{Y}(y)$ es $0$ o una potencia de $\frac{1}{2}$. La segunda propiedad hay que verificarla. Para ello, hay que obtener

\[ \sum_{k=1}^{\infty} p_{Y}(k) = \sum_{k=1}^{\infty} {\left(\frac{1}{2}\right)}^{k}. \]

Podemos hacer uso de la fórmula para una serie geométrica, modificando un poco la expresión anterior. Así,

\begin{align*} \sum_{k = 1}^{\infty} {\left(\frac{1}{2}\right)}^{k} &= \sum_{k = 0}^{\infty} {\left(\frac{1}{2}\right)}^{k+1} \\[1em] &= \sum_{k = 0}^{\infty} {\left(\frac{1}{2}\right)}{\left(\frac{1}{2}\right)}^{k} \\[1em] &= {\left(\frac{1}{2}\right)} \sum_{k = 0}^{\infty} {\left(\frac{1}{2}\right)}^{k} \\[1em] \end{align*}

Así, nos queda una serie geométrica de la forma $\sum_{k=0}^{\infty} ar^{k}$, con $0 < r < 1$, por lo que resulta

\begin{align*} {\left(\frac{1}{2}\right)} \sum_{k = 0}^{\infty} {\left(\frac{1}{2}\right)}^{k} &= {\left(\frac{1}{2}\right)}{\left(\frac{1}{1 − \frac{1}{2} }\right)} \\[1em] &= {\left(\frac{1}{2}\right)}{\left(2\right)} \\[1em] &= 1.\end{align*}

Esto garantiza que $p_{Y}$ es una función que describe el comportamiento probabilístico de una v.a.

Podemos hacer el cálculo de probabilidades de $Y$. Por ejemplo, ¿cuál es la probabilidad de que $Y$ sea $2$ o sea $6$? Para verlo, tenemos que obtener la probabilidad de $(X =2) \cup (X = 6)$. Estos dos conjuntos son ajenos, pues

\[ (X = 2) \cap (X = 6) = X^{-1}[\{ 2 \}] \cap X^{-1}[\{ 6 \}] = X^{-1}[\{ 2 \} \cap \{ 6 \}] = X^{-1}[\emptyset] = \emptyset, \]

así que $\Prob{(X = 2) \cup (X = 6)} = \Prob{X = 2} + \Prob{X = 6}$. Así, tenemos que

\begin{align*} \Prob{(X = 2) \cup (X = 6)} &= \Prob{X = 2} + \Prob{X = 6} \\[1em]
&= p_{Y}(2) + p_{Y}(6) \\[1em] &= \frac{1}{2^{2}} + \frac{1}{2^{6}} \\[1em] &= \frac{1}{4} + \frac{1}{64} \\[1em] &= \frac{17}{64} \approx 0.2656, \\[1em] \end{align*}

así que la probabilidad de que $Y$ tome el valor $2$ o tome el valor $6$ es de aproximadamente $0.2656$, o $26.56\%$. Por otro lado, ¿cuál será la probabilidad de que $Y \leq 5$? Esta es la probabilidad de que tome alguno de los valores $1$, $2$, $3$, $4$ o $5$. En consecuencia, tenemos que

\begin{align*} \Prob{Y \leq 5} &= \Prob{Y = 1} + \Prob{Y = 2} + \Prob{Y = 3} + \Prob{Y = 4} + \Prob{Y = 5} \\[1em] &= \sum_{k=1}^{5} \Prob{Y = k} \\[1em] &= \sum_{k=1}^{5} p_{Y}(k) \\[1em] &= \sum_{k=1}^{5} {\left(\frac{1}{2}\right)}^{k} \\[1em] &= {\left(\frac{1}{2}\right)}\sum_{k=1}^{5} {\left(\frac{1}{2}\right)}^{k−1} \\[1em] &= {\left(\frac{1}{2}\right)}\sum_{k=0}^{4} {\left(\frac{1}{2}\right)}^{k} \\[1em] &= {\left(\frac{1}{2}\right)} {\left(\dfrac{1 − {\left(\frac{1}{2}\right)}^{4+1}}{1 − \frac{1}{2}}\right)} \\[1em] &= {\left(\frac{1}{2}\right)} {\left(\dfrac{1 − {\left(\frac{1}{2}\right)}^{5}}{\frac{1}{2}}\right)} \\[1em] &= {1 − {\left(\frac{1}{2}\right)}^{5}} = 0.96875, \end{align*}

así que la probabilidad de que $Y$ sea menor o igual a $5$ es de $0.96875$, o $96.875\%$. Otra pregunta interesante es, ¿cuál es la probabilidad de que $Y$ sea un número par? Es decir, si $P$ es el conjunto de números naturales pares,

\[ P = \{ n \in \mathbb{N}^{+} \mid \exists k \in \mathbb{N}\colon n = 2k \}, \]

¿cuál es el valor de $\Prob{Y \in P}$? Para verlo, observa que como en las probabilidades anteriores, la probabilidad que queremos calcular puede verse como la suma de las probabilidades de todos los valores en $P$. De este modo, se tiene que

\begin{align*} \Prob{Y \in P} &= \sum_{n \in P} \Prob{Y = n} \\[1em] &= \sum_{k = 1}^{\infty} \Prob{Y = 2k} \\[1em] &= \sum_{k = 1}^{\infty} p_{Y}(k) \\[1em] &= \sum_{k=1}^{\infty} {\left(\frac{1}{2}\right)}^{2k} \\[1em] &= {\left(\frac{1}{2}\right)}^{2}\sum_{k=1}^{\infty} {\left(\frac{1}{2}\right)}^{2k−2} \\[1em] &= {\left(\frac{1}{2}\right)}^{2}\sum_{k=1}^{\infty} {\left(\frac{1}{2}\right)}^{2(k−1)} \\[1em] &= {\left(\frac{1}{2}\right)}^{2}\sum_{k=1}^{\infty} {\left(\frac{1}{2^{2}}\right)}^{k−1} \\[1em] &= {\left(\frac{1}{2}\right)}^{2}\sum_{k=1}^{\infty} {\left(\frac{1}{4}\right)}^{k−1} \\[1em] &= {\left(\frac{1}{2}\right)}^{2}\sum_{k=0}^{\infty} {\left(\frac{1}{4}\right)}^{k} \\[1em] &= {\left(\frac{1}{4}\right)}{\left(\dfrac{1}{1 − \frac{1}{4}}\right)} \\[1em] &= {\left(\frac{1}{4}\right)}{\left(\dfrac{1}{\frac{3}{4}}\right)} \\[1em] &= {\left(\frac{1}{4}\right)}{\left(\dfrac{4}{3}\right)} = \frac{1}{3},\end{align*}

así que la probabilidad de que $Y$ tome como valor un número par es de $\frac{1}{3}$, o $33.333\ldots\%$.

Finalmente, observa que $\mathbb{N}$ y $\mathbb{N}^{+}$ son soportes de $Y$, pues $\Prob{Y \in \mathbb{N}^{+}} = 1$, y como $\mathbb{N}^{+} \subseteq \mathbb{N}$, se tiene que $\Prob{Y \in \mathbb{N}^{+}} \leq \Prob{Y \in \mathbb{N}}$, que implica $\Prob{Y \in \mathbb{N}} = 1$. Esto exhibe que cuando $S$ es un soporte de una v.a. discreta, está asegurado que contiene a todos los valores que puede tomar la v.a., pero no significa que todos los elementos de $S$ tienen probabilidad positiva. Por ejemplo, en este caso tenemos que $\Prob{Y = 0} = 0$ y $0 \in \mathbb{N}$.

Propiedades de una función de masa de probabilidad

Como vimos en el ejemplo anterior (y en la discusión que le precede), la función de masa de probabilidad es suficiente para conocer el comportamiento probabilístico de una v.a. discreta. Por ello, es necesario saber qué propiedades necesita una función cualquiera para ser la función de masa de probabilidad de alguna v.a. discreta $X$.

Sea $p\colon\RR\to\RR$ una función y sea $S = \{ \, s_{i} \mid i \in I \, \} \in \mathscr{B}(\RR)$ un conjunto a lo más numerable de números reales y sea $\{ \pi_{i} \mid i \in I \}$ una colección de números reales tales que

Para cada $i \in I$ se cumple que $\pi_{i} \geq 0$.
Se cumple que\[ \sum_{i \in I} \pi_{i} = 1, \]

si definimos $p\colon\RR\to\RR$ como

\[ p(x) = \begin{cases} \pi_{i} & \text{si $x = s_{i}$, con $i \in I$,} \\[1em] 0 & \text{si $x \notin S$,}\end{cases} \]

entonces existe una v.a. discreta $X$ tal que $p$ es la función de masa de probabilidad de $X$. En efecto, al tomar $F\colon\RR\to\RR$ dada por

\[ F(x) = \sum_{s \in (-\infty, x]} p(s), \quad \text{para cada $x \in \RR$,} \]

se tiene que $F$ es una función de distribución, así que la existencia de $X$ está garantizada por lo que vimos en la entrada de Funciones de Distribución.

En conclusión, si tu cuentas con una colección a lo más numerable $S = \{ \, s_{i} \mid i \in I \, \}$ de números reales, y $\{ \, \pi_{i} \mid i \in I \, \}$ son números reales que se pueden usar como la probabilidad de los elementos de $S$ (de tal manera que $\pi_{i}$ es la probabilidad de $s_{i}$), estos valores definen las probabilidades de que alguna v.a. discreta tome los valores en $S$.

Esto es, existe una v.a. discreta $X$ tal que

\begin{align*} \Prob{X = s_{i}} &= \pi_{i}, \quad \text{para cada $i \in I$.}\end{align*}

Fórmula para la función de distribución a partir de la función de masa de probabilidad

Más adelante veremos algunas v.a.’s que tienen a $\mathbb{N}$ como un soporte. Esto es, la probabilidad de que esas v.a.’s caigan en $\mathbb{N}$ es $1$. Por ello, el conjunto de valores que puede tomar una v.a. de ese tipo es el conjunto de los números naturales, o algún subconjunto de este, como $\mathbb{N}^{+}$ o $\{ 0, 1, \ldots, n \}$, para algún $n \in \mathbb{N}^{+}$. Por ejemplo, ya vimos que $\mathbb{N}$ es un soporte de la v.a. $Y$ del último ejemplo; aún cuando el conjunto de valores que puede tomar $Y$ es $\mathbb{N}^{+}$.

En tales casos, la función de distribución de una v.a. discreta puede escribirse a partir de la función de masa de probabilidad de manera ordenada como sigue. Si $X$ es una v.a. discreta tal que su función de masa de probabilidad es $p_{X}\colon\RR\to\RR$ dada por

\[p_{X}(x) = \begin{cases} \pi_{x} & \text{para cada $x \in \mathbb{N}$,} \\[1em] 0 & \text{si $x \notin \mathbb{N}$}, \end{cases} \]

donde $\{ \pi_{i} \mid i \in \mathbb{N} \}$ son números reales tales que $\pi_{i} \geq 0$ para cada $i \in \mathbb{N}$ y $\sum_{k=0}^{\infty} \pi_{k} = 1$. Entonces la función de distribución de $X$ puede escribirse como

\[ F_{X}(x) = \begin{cases} 0 & \text{si $x < 0$,} \\[1em] \pi_{0} + \pi_{1} + \cdots + \pi_{\lfloor x \rfloor} & \text{si $x \geq 0$}. \end{cases} \]

donde $\lfloor x \rfloor$ es el mayor entero que es menor o igual a $x$. Por ejemplo, $\lfloor \pi \rfloor = 3$ y $\lfloor 6.34 \rfloor = 6$.

Tarea moral

Demuestra que si $X$ es una v.a., entonces se para cada $a \in \RR$ se cumple que\[ F_{X}(a-) = \Prob{X < a}. \]Sugerencia: Aplica el teorema de continuidad de la probabilidad a la sucesión de conjuntos $\{ A_{n} \}_{n\in\mathbb{N}^{+}}$, donde para cada $n\in\mathbb{N}^{+}$ definimos $A_{n} = (-\infty, a − \frac{1}{n}]$.
Retomando el Ejemplo 1, encuentra la probabilidad de que «$X$ tome el valor $1$ o el valor $-1$».
Encuentra la función de distribución de la variable aleatoria $Y$ del Ejemplo 2. Sugerencia: Nosotros obtuvimos $\Prob{Y \leq 5}$, ¿qué pasa si en vez de hacerlo para $5$, lo haces para cualquier $x \in \RR$?

Más adelante…

Más adelante veremos muchas v.a.’s discretas para las cuales $\mathbb{N}$ es un soporte. Como comentamos en la última sección de esta entrada, esto significará que el conjunto de valores que pueden tomar esas v.a.’s es $\mathbb{N}$ o algún subconjunto de $\mathbb{N}$. Por ello, la función de distribución de esas v.a.’s podrá escribirse utilizando la fórmula que obtuvimos en esa sección.

En la siguiente entrada abordaremos las v.a.’s continuas. Así como las v.a.’s discretas, las v.a.’s continuas tienen ciertas peculiaridades importantes que tenemos que analizar.

Entradas relacionadas

Ir a Probabilidad I
Entrada anterior del curso: Funciones de Distribución de Probabilidad
Siguiente entrada del curso: Variables Aleatorias Continuas

Probabilidad I: Funciones de Distribución de Probabilidad

Por Octavio Daniel Ríos García

Deja un comentario

Introducción

Una vez que hemos introducido el concepto de variable aleatoria, nos toca ver qué nuevas definiciones surgen a partir de este. Un primer concepto que surge es la función de distribución. A grandes rasgos, dado un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$, en la entrada anterior vimos que una función $X\colon\Omega\to\RR$ debe de satisfacer que para cualquier $x \in \RR$, $X^{-1}[(-\infty, x]]$ es un evento de $\Omega$. Básicamente, esta condición era suficiente para concluir que para cada $B \in \mathscr{B}(\RR)$ se cumple que $X^{-1}[B] \in \mathscr{F}$. En otras palabras, la imagen inversa de cualquier evento de $\RR$ es un evento de $\Omega$.

De manera similar, lo que haremos será definir la probabilidad de los eventos de la forma $(X \leq x)$, con $x \in \RR$. No lo veremos aquí (porque no tenemos las herramientas suficientes para hacerlo), pero resulta que asignarle probabilidad a esos eventos captura toda la información relevante sobre una variable aleatoria. Esto nos permitirá prescindir por completo de muchos detalles de la variable aleatoria, y centrar nuestra atención en el conjunto de valores que puede tomar.

Funciones de distribución de probabilidad

De manera general, existe un tipo de función que nos va a interesar a partir de ahora, que corresponde a las funciones de distribución de probabilidad. Estas se definen como sigue.

Definición. Sea $F\colon\RR\to\RR$ una función. Diremos que $F$ es una función de distribución de probabilidad si:

$F$ es no-decreciente. Esto es, para cada $a, b \in \RR$, si $a < b$ entonces $F(a) \leq F(b)$.
$F$ es continua por la derecha. Es decir, para cada $a \in \RR$ se cumple que\[ \lim_{x\to a^{+}} F(x) = F(a). \]
Se cumple que\[ \lim_{x\to\infty} F(x) = 1 \quad\text{y}\quad \lim_{x\to -\infty} F(x) = 0. \]

Una función no requiere de ningún contexto adicional para considerarse una función de distribución de probabilidad. Es decir, para que una función $F\colon\RR\to\RR$ sea considerada una función de distribución de probabilidad, simplemente debe de ser no-decreciente, continua por la derecha y sus límites a $\infty$ y $-\infty$ deben de ser $1$ y $0$, respectivamente.

Ejemplo 1. Sean $a, b \in \RR$ tales que $a < b$. La función $F\colon\RR\to\RR$ dada por

\[ F(x) = \begin{cases} 0 & \text{si $x < a$,} \\[1em] \cfrac{x − a}{b − a} & \text{si $a \leq x \leq b$,} \\[1em] 1 & \text{si $b < x$.} \end{cases} \]

es no-decreciente, continua por la derecha y sus límites a $\infty$ y $-\infty$ son $1$ y $0$, así que es una función de distribución de probabilidad. Gráficamente, se ve como sigue.

**Figura.** Gráfica de la función de distribución de probabilidad expuesta en este ejemplo.

Ejemplo 2. Sea $\lambda \in \RR$ tal que $\lambda > 0$. La función $F\colon\RR\to\RR$ dada por

\[ F(x) = \begin{cases} 0 & \text{si $x < 0$,} \\[1em] 1 − e^{-\lambda x} & \text{si $x \geq 0$.} \end{cases} \]

es una función de distribución de probabilidad. Gráficamente:

**Figura.** Gráfica de la función de distribución de probabilidad de este ejemplo.

Función de distribución de una variable aleatoria

Dada cualquier variable aleatoria $X$ sobre un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$, hay una función muy importante asociada a $X$: su función de distribución, definida como sigue.

Definición. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y sea $X\colon\Omega\to\RR$ una variable aleatoria. La función de distribución de $X$ es la función $F_{X}\colon\RR\to[0,1]$ dada por

\[ F_{X}(x) = \Prob{\{\, \omega\in\Omega \mid X(\omega) \leq x \,\}} = \Prob{X \leq x}, \quad \text{para cada $x \in \RR$}. \]

$F_{X}$ también es llamada la función de distribución acumulada de $X$, que en inglés se abrevia como CDF (cumulative distribution function).

Es decir, dada una variable aleatoria $X$, su función de distribución devuelve la probabilidad de que $X$ sea menor o igual a $x$, para cada $x \in\RR$. Como seguramente ya sospechas por el nombre de $F_{X}$, resulta que $F_{X}$ es una función de distribución de probabilidad. Este hecho es demostrado en el siguiente teorema.

Teorema. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y sea $X\colon\Omega\to\RR$ una variable aleatoria. Entonces $F_{X}\colon\RR\to[0,1]$ es una función de distribución de probabilidad.

Demostración. De acuerdo con la definición, para demostrar que $F_{X}\colon\RR\to\RR$ es una función de distribución de probabilidad, tenemos que demostrar 3 cosas:

$F_{X}$ es no-decreciente: para cada $a, b \in \RR$, si $a < b$ entonces $F_{X}(a) \leq F_{X}(b)$.
$F_{X}$ es continua por la derecha: que para cada $a \in \RR$ se cumple que\[ \lim_{x\to a^{+}} F_X(x) = F_{X}(a). \]
Se cumple que\[ \lim_{x\to\infty} F_{X}(x) = 1 \quad\text{y}\quad \lim_{x\to -\infty} F_{X}(x) = 0. \]

Veamos que se cumple 1. Sean $a, b \in \RR$ tales que $a < b$. Ahora, observa que $(a, b] = (-\infty, b] \smallsetminus (-\infty, a]$, por lo que

\begin{align*} \Prob{X^{-1}[(a, b]]} &= \Prob{X^{-1}[(-\infty, b] \smallsetminus (-\infty, a]]} \\[0.5em] &= \Prob{X^{-1}[(-\infty, b]] \smallsetminus X^{-1}[(-\infty, a]]}. \end{align*}

Como $a < b$, se cumple que $(-\infty, a] \subseteq (-\infty, b]$, por lo que

\[ X^{-1}[(-\infty, a]] \subseteq X^{-1}[(-\infty, b]], \]

así que $\Prob{X^{-1}[(-\infty, b]] \smallsetminus X^{-1}[(-\infty, a]]} = \Prob{X^{-1}[(-\infty, b]]} − \Prob{X^{-1}[(-\infty, a]]}$. En consecuencia, tenemos que

\begin{align*} \Prob{X^{-1}[(a, b]]} &= \Prob{X^{-1}[(-\infty, b]]} − \Prob{X^{-1}[(-\infty, a]]} \\[0.5em] &= \Prob{X \leq b} − \Prob{X \leq a} \\[0.5em] &= F_{X}(b) − F_{X}(a). \end{align*}

Recuerda que $\mathbb{P}$ es una medida de probabilidad, por lo que $\Prob{X^{-1}[(a, b]]} \geq 0$; que implica $F_{X}(b) − F_{X}(a) \geq 0$, o equivalentemente, que $F_{X}(b) \geq F_{X}(a)$. En conclusión, para cualesquiera $a, b \in \RR$ tales que $a < b$, se cumple que $F_{X}(a) \leq F_{X}(b)$, que es justamente lo que queríamos demostrar. Por lo tanto, $F_{X}$ es una función no-decreciente.

Para demostrar 2, sea $(x_{n})_{n\in\mathbb{N}^{+}} \subseteq \RR$ una sucesión monótona decreciente de números reales tal que su límite es $0$. Es decir, $x_{1} > x_{2} > x_{3} > \cdots$ y

\[ \lim_{n\to\infty} x_{n} = 0. \]

Ahora, sea $a \in \RR$. Definimos la sucesión de eventos $\{ A_{n} \}_{n\in\mathbb{N}^{+}}$ tal que para cada $n \in \mathbb{N}^{+}$, $A_{n} = ( X \leq a + x_{n} )$. De este modo, se tiene que

\[ \bigcap_{n=1}^{\infty} A_{n} = (X \leq a), \]

pues la sucesión $(x_{n})_{n\in\mathbb{N}^{+}}$ converge a $0$. Ahora, por el teorema de continuidad de la probabilidad, tenemos que

\[ F_{X}(a) = \Prob{X \leq a} = \Prob{\bigcap_{n=1}^{\infty} A_{n}} = \lim_{n\to\infty} \Prob{A_{n}} = \lim_{n\to\infty} \Prob{X \leq a + x_{n}} = \lim_{n\to\infty} F_{X}(a + x_{n}), \]

es decir, $\lim_{n\to\infty} F_{X}(a + x_{n}) = F_{X}(a)$, para cualquier $a \in \RR$ y cualquier sucesión monótona decreciente $(x_{n})_{n\in\mathbb{N}^{+}}$. Por ello, se puede concluir que $F_{X}$ es una función continua por la derecha.

Finalmente, en 3 demostraremos que el límite de $F_{X}(x)$ cuando $x\to\infty$ es $1$. La demostración del otro límite es muy parecida. Sea $(x_{n})_{n\in\mathbb{N}^{+}} \subseteq \RR$ una sucesión de números reales tal que $x_{1} \leq x_{2} \leq x_{3} \leq \cdots$ y $\lim_{n\to\infty} x_{n} = \infty$. Para cada $n \in \mathbb{N}^{+}$ definimos

\[ A_{n} = (X \leq x_{n}) = X^{-1}[(-\infty, x_{n}]]. \]

De esta forma, tenemos que $\{ A_{n} \}_{n\in\mathbb{N}^{+}}$ es una sucesión creciente de eventos, pues observa que $A_{1} \subseteq A_{2} \subseteq A_{3} \subseteq \cdots$ De este modo, como supusimos que $(x_{n})_{n\in\mathbb{N}^{+}}$ es una sucesión que diverge a $\infty$, se tiene que

\[ \bigcup_{n=1}^{\infty} A_{n} = \bigcup_{n=1}^{\infty}(X \leq x_{n}) = \bigcup_{n=1}^{\infty}X^{-1}[(-\infty, x_{n}]] = X^{-1}{\left[ \bigcup_{n=1}^{\infty} (-\infty, x_{n}] \right]} = X^{-1}[\RR] = \Omega. \]

Ahora, aplicando el teorema de la continuidad de la probabilidad a $\{ A_{n}\}_{n\in\mathbb{N}^{+}}$ y usando que la sucesión $(x_{n})_{n\in\mathbb{N}^{+}}$ es divergente, tenemos que

\begin{align*} \lim_{x\to\infty} F_{X}(x) &= \lim_{n\to\infty} F_{X}(x_{n}) \\ &= \lim_{n\to\infty}\Prob{X \leq x_{n}} \\ &= \lim_{n\to\infty}\Prob{A_{n}} \\ &= \Prob{\bigcup_{n=1}^{\infty} A_{n}} \\ &= \Prob{\Omega} \\ &= 1. \end{align*}

En conclusión, tenemos que

\[ \lim_{x\to\infty} F_{X}(x) = 1, \]

que es justamente lo que queríamos demostrar. La demostración de que el límite a $-\infty$ de $F_{X}$ es $0$ se obtiene de manera casi análoga, pero la familia de eventos que se plantea es decreciente, y se utiliza el teorema de continuidad de la probabilidad para ese caso.

$\square$

Partiendo de una función de distribución de probabilidad

Por el teorema anterior, vimos que la función de distribución de cualquier variable aleatoria es también una función de distribución de probabilidad. Es decir, que si tienes un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$ y una variable aleatoria $X\colon\Omega\to\RR$, la función de distribución de $X$, $F_{X}\colon\RR\to[0,1]$, es una función de distribución de probabilidad.

Por otro lado, ahora imagina que te encuentras con una función $F\colon\RR\to\RR$ que es una función de distribución de probabilidad. No obstante, observa que no sabes nada más sobre esta función. Es decir, no hay ninguna variable aleatoria ni un espacio de probabilidad a la vista… ¿Será posible que $F$ provenga de alguna variable aleatoria $X$ definida sobre un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$?

En otras palabras: dada $F\colon\RR\to\RR$ una función de distribución de probabilidad, ¿siempre existen un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$ y una variable aleatoria $X\colon\Omega\to\RR$ tal que $F$ es la función de distribución de $X$? ¡La respuesta es que sí! A grandes rasgos, $F$ define la probabilidad de los eventos de la forma $(-\infty, x]$, para cada $x \in \RR$. Esto resulta suficiente para definir por completo la medida de probabilidad inducida por una variable aleatoria $X$… pero, ¿cuál variable aleatoria $X$? De manera canónica, siempre puede utilizarse la variable aleatoria identidad sobre $\Omega = \RR$, que es la función $X\colon\RR\to\RR$ tal que para cada $\omega\in\RR$, $X(\omega) = \omega$. De este modo, la medida de probabilidad inducida por $X$ es la misma que la medida en el dominio de $X$, que en este caso es $\RR$ con $\mathscr{B}(\RR)$ como σ-álgebra, y usando la medida determinada por $F$.

¡CUIDADO! Esto NO significa que todas las variables aleatorias son simplemente la función identidad. Lo que significa es que siempre que tengas una función de distribución de probabilidad $F\colon\RR\to\RR$, está garantizado que existen un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$ y una variable aleatoria $X\colon\Omega\to\RR$ de tal forma que $F$ es la función de distribución de $X$. La existencia está garantizada porque, al menos, siempre se puede usar la función identidad de $\RR$ en $\RR$ como variable aleatoria, pero puede haber otras distintas cuya función de distribución también es $F$.

Los siguientes ejemplos son largos, pero capturan muchas de las ideas vistas hasta ahora sobre variables aleatorias. Además, en conjunto, estos dos ejemplos exhiben lo que comentamos en el párrafo anterior.

Ejemplo 3. Sea $\Omega = \{ 0, 1\}^{3}$. Es decir, $\Omega$ es el conjunto

\[ \Omega = \{ (0,0,0), (0,0,1), (0,1,0), (1,0,0), (0,1,1), (1,0,1), (1,1,0), (1,1,1) \}. \]

$\Omega$ puede pensarse como el espacio muestral de un experimento aleatorio en el que se hacen $3$ ensayos de un experimento aleatorio que tiene dos resultados posibles: éxito o fracaso. Por ejemplo, el lanzamiento de una moneda («águila» o «sol»). Tomaremos como σ-algebra de $\Omega$ a $\mathscr{P}(\Omega)$, la potencia de $\Omega$.

Sea $p \in \RR$ tal que $p \in [0,1]$. Plantearemos una medida de probabilidad tal que los $3$ ensayos son independientes. Para ello, para cada $k \in \{1,2,3\}$ planteamos los eventos

$A_{k}$: el evento de que el $k$-ésimo ensayo sea un éxito. Es decir, $A_{k}$ es el evento\[ A_{k} = \{\, (\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega \mid \omega_{k} = 1 \,\}. \]
$B_{k}$: el evento de que el $k$-ésimo ensayo sea un fracaso. Es decir, $B_{k}$ es el evento\[ B_{k} = \{\, (\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega \mid \omega_{k} = 0 \,\}. \]

Observa que para cada $k \in \{1,2,3\}$ se cumple que $B_{k} = A_{k}^{\mathsf{c}}$. Por ejemplo, $A_{2}$ es el evento

\[ A_{2} = \{\, (\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega \mid \omega_{2} = 1 \,\} = \{ (0,1,0), (0,1,1), (1,1,0), (1,1,1) \} \]

Comenzamos a definir la medida de probabilidad $\mathbb{P}\colon\mathscr{P}(\Omega)\to\RR$ como sigue: para cada $k \in \{1,2,3\}$ definimos

\[ \Prob{A_{k}} = p, \]

\[ \Prob{B_{k}} = 1 − p, \]

y pedimos que $\mathbb{P}$ sea tal que los eventos $A_{1}$, $A_{2}$ y $A_{3}$ son independientes. En consecuencia, se cumple lo siguiente

\begin{align} \Prob{A_{1} \cap A_{2} \cap A_{3}} &= \Prob{A_{1}}\Prob{A_{2}}\Prob{A_{3}} = p^{3} \\[1em] \Prob{B_{1} \cap A_{2} \cap A_{3}} &= \Prob{B_{1}}\Prob{A_{2}}\Prob{A_{3}} = (1 − p)p^{2} = p^{2}(1 − p) \\[1em] \Prob{A_{1} \cap B_{2} \cap A_{3}} &= \Prob{A_{1}}\Prob{B_{2}}\Prob{A_{3}} = p(1 − p)p = p^{2}(1 − p) \\[1em] \Prob{A_{1} \cap A_{2} \cap B_{3}} &= \Prob{A_{1}}\Prob{A_{2}}\Prob{B_{3}} = p^{2}(1 − p), \\[1em] \Prob{B_{1} \cap B_{2} \cap A_{3}} &= \Prob{B_{1}}\Prob{B_{2}}\Prob{A_{3}} = (1 − p)^{2}p = p(1 − p)^{2}, \\[1em] \Prob{B_{1} \cap A_{2} \cap B_{3}} &= \Prob{B_{1}}\Prob{A_{2}}\Prob{B_{3}} = (1− p)p(1− p) = p(1 − p)^{2}, \\[1em] \Prob{A_{1} \cap B_{2} \cap B_{3}} &= \Prob{A_{1}}\Prob{B_{2}}\Prob{B_{3}} = p(1 − p)^{2}, \\[1em] \Prob{B_{1} \cap B_{2} \cap B_{3}} &= \Prob{B_{1}}\Prob{B_{2}}\Prob{B_{3}} = (1 − p)^{3}. \\[1em] \end{align}

De hecho, observa que estas condiciones son suficientes para definir la probabilidad de cada resultado, y así, la de cada evento $A \in \mathscr{P}(\Omega)$. Por ejemplo, nota que

\[ A_{1} \cap A_{2} \cap A_{3} = \{ \, (\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega \mid \omega_{1} = 1 \land \omega_{2} = 1 \land \omega_{3} = 1 \, \} = \{ (1,1,1) \}, \]

y por lo anterior, $\Prob{A_{1} \cap A_{2} \cap A_{3}} = p^{3}$. Por lo tanto, se concluye que

\[ \Prob{\{(1,1,1)\}} = p^{3}. \]

Los $8$ elementos de $\Omega$ pueden verse como las intersecciones de las identidades $(1)$ a $(8)$, así que la probabilidad de cada uno está determinada por cada una de esas igualdades. Por ejemplo, además de la anterior ($\Prob{\{(1,1,1)\}} = p^{3}$), observa que

\[ A_{1} \cap B_{2} \cap B_{3} = \{ \, (\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega \mid \omega_{1} = 1 \land \omega_{2} = 0 \land \omega_{3} = 0 \, \} = \{ (1,0,0) \}, \]

por lo que $\Prob{\{(1,0,0)\}} = p(1−p)^{2}$. Ahora, presta atención a los exponentes de $p$ y de $1−p$ en estas probabilidades, y compáralos con el número de $1$’s y $0$’s de las ternas ordenadas. ¿Qué puedes observar? Resulta que el exponente de la $p$ es el número de $1$’s, es decir, el número de éxitos. Por otro lado, el exponente del $1−p$ es el número de $0$’s, es decir, el número de fracasos.

Ahora, para cada $\mathbf{a} \in \Omega$, $\mathbf{a}$ puede escribirse como $\mathbf{a} = (a_{1}, a_{2}, a_{3})$, con $a_{1}$, $a_{2}$, $a_{3} \in \{0,1\}$. En consecuencia, el número de éxitos en la terna $\mathbf{a}$ puede escribirse como

\[ {\lVert \mathbf{a} \rVert}_{1} = {\left\lVert (a_{1}, a_{2}, a_{3}) \right\rVert}_{1} = |a_{1}| + |a_{2}| + |a_{3}|. \]

Por el contrario, el número de fracasos en la terna $\mathbf{a}$ puede escribirse como

\[ 3 − {\lVert \mathbf{a} \rVert}_{1} = 3 − {\left\lVert (a_{1}, a_{2}, a_{3}) \right\rVert}_{1} = 3 − (|a_{1}| + |a_{2}| + |a_{3}|). \]

De este modo, para cada $\mathbf{a} \in \Omega$, se tiene que

\[ \Prob{\{\mathbf{a}\}} = p^{{\lVert \mathbf{a} \rVert}_{1}} (1−p)^{3 − {\lVert \mathbf{a}\rVert}_{1}}. \]

Por esta razón, definimos a la medida de probabilidad $\mathbb{P}\colon\mathscr{P}(\Omega) \to \RR$ dada por

\[ \Prob{A} = \sum_{\mathbf{a}\in A} p^{{\lVert \mathbf{a} \rVert}_{1}} (1−p)^{3 − {\lVert \mathbf{a}\rVert}_{1}}, \quad \text{para cada $A \in \mathscr{P}(\Omega)$.}\]

Ahora, definimos a la variable aleatoria $X\colon\Omega\to\RR$ como sigue. Para cada $\mathbf{a}\in\Omega$, se define

\[ X(\mathbf{a}) = \lVert \mathbf{a} \rVert_{1}, \]

por lo que si $\mathbf{a} = (a_{1}, a_{2}, a_{3})$, se tiene que

\[ X(\mathbf{a}) = |a_{1}| + |a_{2}| + |a_{3}|. \]

Por ejemplo, $X(1,0,1) = 1 + 0 + 1 = 2$, y $X(1,1,1) = 1+1+1 = 3$. Es decir, $X$ contabiliza el número de éxitos en los $3$ ensayos. Observa que el conjunto de valores que puede tomar $X$ es $\{ 0, 1, 2, 3 \}$. Obtengamos la probabilidad de que $X$ tome cada uno de estos valores.

\begin{align*} \Prob{X = 0} = \Prob{\{\, \omega \in \Omega \mid X(\omega) = 0 \,\}} &= \Prob{\{ (0,0,0) \}} \\[0.5em] &= (1−p)^{3}, \\[1.5em] \Prob{X = 1} = \Prob{\{\, \omega \in \Omega \mid X(\omega) = 1 \,\}} &= \Prob{\{ (1,0,0), (0,1,0), (0,0,1) \}} \\[0.5em] &= p(1−p)^{2} + p(1−p)^{2} + p(1−p)^{2} \\[0.5em] &= 3p(1−p)^{2}, \\[1.5em] \Prob{X = 2} = \Prob{\{\, \omega \in \Omega \mid X(\omega) = 2 \,\}} &= \Prob{\{ (1,1,0), (1,0,1), (0,1,1) \}} \\[0.5em] &= p^{2}(1−p) + p^{2}(1−p) + p^{2}(1−p) \\[0.5em] &= 3p^{2}(1−p), \\[1.5em] \Prob{X = 3} = \Prob{\{\, \omega \in \Omega \mid X(\omega) = 3 \,\}} &= \Prob{\{ (1,1,1) \}} \\[0.5em] &= p^{3}. \end{align*}

Ahora obtengamos la función de distribución de $X$. Esto es,

\[ F_{X}(x) = \Prob{X \leq x}. \]

Primero, observa que para cada $x \in (-\infty, 0)$ se tiene que $F_{X}(x) = 0$, pues la variable aleatoria no toma valores negativos. Después,

\[ F_{X}(0) = \Prob{X \leq 0} = \Prob{\{\, \omega \in \Omega \mid X(\omega) \leq 0 \,\}} = \Prob{\{ (0,0,0) \}} = (1−p)^{3}. \]

Por otro lado, para cada $x \in (0,1)$, observa que

\[ F_{X}(x) = \Prob{X \leq x} = \Prob{\{\, \omega \in \Omega \mid X(\omega) \leq x \,\}} = \Prob{\{ (0,0,0) \}}. \]

porque el único $\omega \in \Omega$ que hace que $X(\omega) \leq x$ es $\omega = (0,0,0)$, para todos los demás, $X(\omega)$ vale al menos $1$, que es mayor a $x$. Luego, tenemos que

\begin{align*} F_{X}(1) = \Prob{X \leq 1} &= \Prob{\{\, \omega \in \Omega \mid X(\omega) \leq 1 \,\}} \\[0.5em] &= \Prob{\{ (0,0,0), (0,0,1), (0,1,0), (1,0,0) \}} \\[0.5em] &= (1−p)^{3} + 3p(1−p)^{2}, \end{align*}

Observa que ahí se acumularon los elementos de $\Omega$ que hacen que $X(\omega) = 0$ y $X(\omega) = 1$, pues son todos los valores que toma la variable aleatoria que son menores o iguales a $1$.

Después, para cada $x\in(1,2)$, los $\omega\in\Omega$ que hacen que $X(\omega) \leq x$ son los mismos que en el caso anterior, por lo que $F_{X}(x) = F_{X}(1)$. Continuando de esta manera, se llega a que

\begin{align*} F_{X}(2) &= (1−p)^{3} + 3p(1−p)^{2} + 3p^{2}(1−p), \\[0.5em] F_{X}(x) &= F_{X}(2) & \text{para cada $x \in (2,3)$,} \\[0.5em] F_{X}(3) &= (1−p)^{3} + 3p(1−p)^{2} + 3p^{2}(1−p) + p^{3}, \\[0.5em] F_{X}(x) &= F_{X}(3) & \text{para cada $x \in (3,\infty)$.} \end{align*}

Observa que la expresión para $F_{X}(3)$ corresponde a $(p + (1−p))^{3}$, por el teorema del binomio. En consecuencia, $F_{X}(3) = (p + (1−p))^{3} = 1^3 = 1$. De este modo, obtenemos que la función de distribución de $X$ es la función dada por

\[ F_{X}(x) = \begin{cases} 0 & \text{si $x < 0$,} \\[1em] (1−p)^{3} & \text{si $0 \leq x < 1$,} \\[1em] (1−p)^{3} + 3p(1−p)^{2} & \text{si $1 \leq x < 2$,} \\[1em] (1−p)^{3} + 3p(1−p)^{2} + 3p^{2}(1−p) & \text{si $2 \leq x < 3$,} \\[1em] 1 & \text{si $3 \leq x$.} \end{cases} \]

Nota que a pesar de ser una función con discontinuidades (es una función escalonada), $F_{X}$ sí es continua por la derecha. Observa que también es no-decreciente, y sus límites a $-\infty$ y a $\infty$ son $0$ y $1$, respectivamente; algo que ya esperábamos por el teorema demostrado en esta entrada.

**Figura.** Gráfica de la función $F_{X}$. Es una función escalonada, continua por la derecha. Sus discontinuidades las representamos como círculos sin relleno. Para hacer la gráfica, utilizamos el valor $p = \frac{1}{2}$.

Ejemplo 4. Ahora sea $F\colon\RR\to\RR$ la siguiente función de distribución de probabilidad:

\[ F(x) = \begin{cases} 0 & \text{si $x < 0$,} \\[1em] (1−p)^{3} & \text{si $0 \leq x < 1$,} \\[1em] (1−p)^{3} + 3p(1−p)^{2} & \text{si $1 \leq x < 2$,} \\[1em] (1−p)^{3} + 3p(1−p)^{2} + 3p^{2}(1−p) & \text{si $2 \leq x < 3$,} \\[1em] 1 & \text{si $3 \leq x$.} \end{cases} \]

¡Es la función de distribución de la variable aleatoria $X$ del ejemplo pasado! Sin embargo, nota que aquí te la estamos dando sin ninguna información sobre el espacio de probabilidad subyacente, ni sobre la variable aleatoria involucrada. En primer lugar, ya tenemos garantizado que existe el espacio de probabilidad $(\{0,1\}^{3}, \mathscr{P}(\{0,1\}^{3}), \mathbb{P})$ y la variable aleatoria $X\colon\{0,1\}^{3}\to\RR$ dada por $X(\omega) = {\lVert \omega \rVert}_{1}$, para cada $\omega\in\{0,1\}^{3}$ de tal forma que $F$ es la función de distribución de $X$.

No obstante, observa que podemos definir otra variable aleatoria que resulta en la misma función de distribución. Para ello, toma a $(\RR, \mathscr{B}(\RR), \mathbb{P})$, donde $\mathbb{P}$ es la medida de probabilidad $\mathbb{P}\colon\mathscr{B}(\RR)\to\RR$ definida como sigue: para cada $x\in\RR$, definimos

\[ \Prob{(-\infty, x]} = F(x). \]

Ojo: Esto define la probabilidad de los elementos de $\mathscr{B}(\RR)$ (que son eventos) que tienen la forma $(-\infty, x]$, para cada $x \in \RR$. A su vez, esto define la probabilidad de los eventos de la forma $(a, b]$, para cada $a$, $b \in \RR$ tales que $a < b$, que es

\[ \Prob{(a,b]} = F(b) − F(a), \]

que se puede extender de manera única a una medida sobre todo $\mathscr{B}(\RR)$. Esto es algo que puede demostrarse, pero carecemos de las herramientas para hacerlo en este curso. De cualquier modo, la variable aleatoria que utilizamos en este caso es $Y\colon\RR\to\RR$, la función identidad, dada por

\[ Y(\omega) = \omega, \quad \text{para cada $\omega \in \RR$.} \]

De este modo, se tiene que

\begin{align*} (Y \leq y) &= \{ \, \omega \in \RR \mid Y(\omega) \leq y \, \} \\[0.5em] &= \{ \, \omega \in \RR \mid \omega \leq y \, \} \\[0.5em] &= (-\infty, y], \end{align*}

y por lo tanto, para cada $y \in \RR$,

\[ F_{Y}(y) = \Prob{Y \leq y} = \Prob{(-\infty, y]} = F(y), \]

por lo que la función de distribución de $Y$ es precisamente la función de distribución de probabilidad que escogimos al comenzar este ejemplo. De este modo, $Y$ es una variable aleatoria que puede tomar los valores $0$, $1$, $2$ y $3$… ¡con las mismas probabilidades que la variable aleatoria $X$ del ejemplo pasado! Sin embargo, ¡los espacios de probabilidad sobre los que estas están definidas son completamente distintos! Esto exhibe que lo más importante de una variable aleatoria es su función de distribución, pues esta determina los valores que puede tomar, y la probabilidad con la que los toma. Es decir, la función de distribución caracteriza el comportamiento probabilístico de una variable aleatoria.

¡Presta mucha atención a los últimos dos ejemplos! La conclusión es que el espacio de probabilidad que subyace a una variable aleatoria realmente no importa. Por ello, en muchos libros de probabilidad (y en este mismo curso), no le prestan atención a esto. Comúnmente, te dan una función $F$ que es una función de distribución de probabilidad, y te dicen «sea $X$ una variable aleatoria con distribución $F$». Con eso es suficiente, pues $F$ determina las probabilidades de todos los eventos que involucran a $X$, sin importar quiénes son $X$ y el espacio de probabilidad sobre el que ésta se define.

Tarea moral

Determina si la función $F\colon\RR\to\RR$ dada por\[F(x) = \begin{cases} 0 & \text{si $x \leq -1$,} \\[0.5em] \frac{1}{2}(x+1)^2 & \text{si $-1 < x \leq 0$,} \\[0.5em] 1 − \frac{1}{2}(1 − x)^{2} & \text{si $0 < x < 1$,} \\[0.5em] 1 &\text{si $x \geq 1$} \end{cases} \]es una función de distribución de probabilidad. Utiliza su gráfica para auxiliarte, en caso de que lo necesites.
Demuestra que el límite a $-\infty$ de la función de distribución de una variable aleatoria es $0$ Sugerencia: Revisa la demostración de la propiedad 3 que vimos en el teorema de esta entrada.
¿Podrías idear más variables que tengan la misma función de distribución del Ejemplo 3? Por ejemplo, si $\Omega_{2} = \{0,2\}^{3}$, decimos que $2$ representa éxito; y definimos $Z\colon\Omega_{2}\to\RR$ como la función dada por\begin{align*} Z(\omega_{1}, \omega_{2}, \omega_{3}) &= \frac{\omega_{1} + \omega_{2} + \omega_{3}}{2} & \text{para cada $(\omega_{1}, \omega_{2}, \omega_{3}) \in \Omega_{2}$,} \end{align*}¿tiene $Z$ la misma distribución que la $X$ del Ejemplo 3?

Más adelante…

Lo siguiente que haremos en el curso es ver los dos tipos de variables aleatorias más importantes que hay, las discretas y las continuas. A grandes rasgos, las discretas son aquellas que pueden tomar una cantidad a lo más numerable de valores distintos, mientras que las continuas son aquellas que pueden tomar una cantidad no-numerable de valores. Es decir, pueden tomar valores en un conjunto cuya cardinalidad es igual a la de $\RR$. En la siguiente entrada abordaremos las particularidades de las variables aleatorias discretas.

Entradas relacionadas

Ir a Probabilidad I
Entrada anterior del curso: Variables Aleatorias
Siguiente entrada del curso: Variables Aleatorias Discretas

Probabilidad I: Variables Aleatorias

Por Octavio Daniel Ríos García

Deja un comentario

Introducción

En la entrada pasada concluimos la primera unidad del curso. Con esto finaliza nuestro estudio general de las medidas de probabilidad. Por otro lado, el contenido de la segunda unidad está enfocado el estudio de las variables aleatorias y sus propiedades.

En esta entrada abordaremos el concepto de variable aleatoria. A grandes rasgos, una variable aleatoria es una función que actúa sobre un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$ y devuelve valores numéricos. Sin embargo, no cualquier función puede considerarse una variable aleatoria. Básicamente, una función será una variable aleatoria si algunas de sus imágenes inversas son eventos de $\Omega$. Esto garantizará que se puede calcular la probabilidad de sus valores, y por tanto, podremos calcular la probabilidad de que la variable aleatoria tome valores específicos.

Ideas preliminares

Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad. Es posible que nos interese algún valor numérico asociado a los resultados del experimento en cuestión. Por ejemplo, considerando el experimento de lanzar una moneda $4$ veces de manera equiprobable, sabemos que su espacio muestral es

\[ \Omega = \begin{Bmatrix} \mathrm{AAAA}, & \mathrm{AAAS}, & \mathrm{AASA}, & \mathrm{ASAA}, \\ \mathrm{SAAA}, & \mathrm{AASS}, & \mathrm{ASAS}, & \mathrm{SAAS}, \\ \mathrm{ASSA}, & \mathrm{SASA}, & \mathrm{SSAA}, & \mathrm{SSSA}, \\ \mathrm{SSAS}, & \mathrm{SASS}, & \mathrm{ASSS}, & \mathrm{SSSS} \end{Bmatrix}. \]

y tomamos a $\mathscr{P}(\Omega)$ como σ-álgebra, y como medida a la medida de probabilidad clásica. Una variable asociada a este experimento es la cantidad de águilas que salieron en los $4$ lanzamientos. Esto podríamos definirlo como una función $X\colon \Omega \rightarrow \RR$, tal que para cada $\omega \in \Omega$ se define

\[ X(\omega) = \text{# de $\mathrm{A}$’s en $\omega$}. \]

De este modo, se tiene que

\begin{align*} &X(\mathrm{AAAS}) = 3, \\ &X(\mathrm{ASAS}) = 2, \end{align*}

\begin{align*} &X(\mathrm{ASSS}) = 1, \\ &X(\mathrm{AAAA}) = 4, \end{align*}

etcétera. Al ser una función, $X$ tiene todas las cualidades y propiedades de una función que viste en álgebra superior. En particular, hay un concepto que nos interesa mucho: la imagen inversa de cada uno de los valores que toma $X$. Como recordatorio, dado $B \subseteq \RR$, la imagen inversa de $B$ bajo $X$ es el conjunto

\[ X^{-1}[B] = \{ \, \omega \in \Omega \mid X(\omega) \in B \, \}. \]

Cuando $B$ es un conjunto de la forma $B = \{ x \}$, con $x \in \RR$, se tiene que

\[ X^{-1}[\{x \}] = \{ \, \omega \in \Omega \mid X(\omega) = x \, \}. \]

Por ejemplo, para la función $X$ como la definimos, podemos observar que

\[ X^{-1}[\{ 2 \}] = \{ \, \omega \in \Omega \mid X(\omega) = 2 \, \} = \{ \mathrm{AASS}, \mathrm{ASAS}, \mathrm{SAAS}, \mathrm{ASSA}, \mathrm{SASA}, \mathrm{SSAA} \}. \]

Ahora, observa que $X^{-1}[{ 2 }] \in \mathscr{P}(\Omega)$, por lo que le podemos asignar una probabilidad. En consecuencia, se tiene que

\begin{align*} \Prob{X^{-1}[\{ 2 \}]} = \Prob{\{ \, \omega \in \Omega \mid X(\omega) = 2 \, \}} &= \frac{|\{ \mathrm{AASS}, \mathrm{ASAS}, \mathrm{SAAS}, \mathrm{ASSA}, \mathrm{SASA}, \mathrm{SSAA} \}|}{|\Omega|} \\ &= \frac{6}{16} \\[1.15em] &= 0.375. \end{align*}

Gracias a esto, podemos decir que «la probabilidad de que $X$ tome el valor $2$ es $\frac{6}{16} = 0.375$». Es decir, le podemos asignar probabilidad a los posibles resultados de $X$. Una notación muy frecuente en el contexto de la probabilidad es la siguiente: usaremos $(X \in B)$ para denotar a $\{ \, \omega \in \Omega \mid X(\omega) \in B \,\} = X^{-1}[B]$, de tal forma que

\[ \Prob{\{ \, \omega \in \Omega \mid X(\omega) \in B \,\}} = \Prob{X \in B}. \]

Del mismo modo, cuando $B = \{x\}$, con $x \in \RR$, se adopta la notación $( X = x )$ para denotar al conjunto $\{ \, \omega \in \Omega \mid X(\omega) = x \,\} = X^{-1}{\left[\{ x \}\right]}$, de tal forma que

\[ \Prob{\{ \, \omega \in \Omega \mid X(\omega) = x \,\}} = \Prob{X = x}. \]

De este modo, en este ejemplo tenemos que $\Prob{X = 2} = 0.375$. Del mismo modo, se utilizará la notación $(X \leq x)$ para denotar a $\{ \, \omega \in \Omega \mid X(\omega) \leq x \, \} = X^{-1}[(-\infty, x]]$. Sin embargo, ¡ten cuidado! Esta es una NOTACIÓN para facilitar la escritura de muchas de las expresiones matemáticas que involucran variables aleatorias. Aunque resulte práctica, no olvides lo que representa realmente.

Definición de variable aleatoria

De acuerdo con la motivación anterior, presentamos la definición de variable aleatoria.

Definición. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad. Diremos que una función $X\colon\Omega \to \RR$ es una variable aleatoria si para cada $B \in \mathscr{B}(\RR)$ se cumple que $X^{-1}[B] \in \mathscr{F}$.

Es decir, $X$ es una variable aleatoria si la imagen inversa bajo $X$ de cualquier evento del σ-álgebra de Borel, es un evento de $\mathscr{F}$.

En algunos contextos se usa la notación $X\colon(\Omega, \mathscr{F})\to(\RR, \mathscr{B}(\RR))$ para denotar a una variable aleatoria. Usando esta notación, se escribe explícitamente el σ-álgebra del dominio y del codominio de $X$.

Intuitivamente, una variable aleatoria es un valor numérico asociado al resultado de un experimento aleatorio. Por ejemplo, cuando hicimos el experimento de lanzar una moneda $4$ veces, el valor numérico asociado a cada uno de los posibles resultados del experimento es la cantidad de águilas que salieron en los $4$ lanzamientos.

Además, previamente acordamos que los elementos de un σ-álgebra son aquellos que se pueden medir, pues el dominio de la medida $\mathbb{P}$ es el σ-álgebra. Esencialmente, la definición de variable aleatoria pide que la función preserve la medibilidad. Es decir, que si $A$ es un subconjunto medible del codominio de $X$ (esto es, $A \in \mathscr{B}(\RR)$), entonces $X^{-1}[A]$ debe de ser un subconjunto medible del dominio de $X$; es decir, $X^{-1}[A] \in \mathscr{F}$. De este modo,

\[ \Prob{X \in A} = \Prob{X^{-1}[A]} = \Prob{\{\, \omega\in\Omega\mid X(\omega) \in A \,\}}, \]

es un valor que está bien definido, pues $X^{-1}[A] \in \mathscr{F}$ y $\mathrm{Dom}(\mathbb{P}) = \mathscr{F}$.

Una propiedad muy importante de las variables aleatorias

Hay libros introductorios a la probabilidad que prefieren no tocar con mucho detalle la definición de variable aleatoria, o darla de manera distinta. Por ejemplo, tal es el caso de A First Course In Probability de Sheldon M. Ross, o Introducción a la Probabilidad de Luis Rincón. En particular, el caso del libro del Dr. Rincón es importante, pues es el libro al que muchos estudiantes recurren al cursar esta materia. Dicho libro ofrece una definición de variable aleatoria distinta; con el siguiente teorema veremos que es equivalente a la que hemos dado aquí.

Teorema. Sean $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y $X\colon\Omega\to\RR$ una función. Si $\mathcal{G} \subseteq \RR$ es un conjunto tal que $\sigma(\mathcal{G}) = \mathscr{B}(\RR)$, entonces las siguientes proposiciones son equivalentes:

$X\colon\Omega\to\RR$ es una variable aleatoria.
Para todo $A \in \mathcal{G}$ se cumple que $X^{-1}[A] \in \mathscr{F}$.

Demostración. $(1 \implies 2)$ Verificar que 1. implica a 2. no es complicado. Supongamos que $X$ es una variable aleatoria. Por definición, esto asegura que para cada $E \in \mathscr{B}(\RR)$ se cumple que $X^{-1}[E] \in \mathscr{F}$.

Ahora, hay que demostrar que 2. es cierto. Sea $A \in \mathcal{G}$. Sabemos que $\sigma(\mathcal{G}) = \mathscr{B}(\RR)$, es decir, el σ-álgebra generado por $\mathcal{G}$ es el σ-álgebra de Borel sobre $\RR$. Además, sabemos que $\sigma(\mathcal{G})$ satisface $\mathcal{G} \subseteq \sigma(\mathcal{G})$, por lo que $\mathcal{G} \subseteq \mathscr{B}(\RR)$. En consecuencia, $A \in \mathscr{B}(\RR)$, que implica $X^{-1}[A] \in \mathscr{F}$, pues $X$ es una variable aleatoria, garantizando que 2. es verdadero.

$(2 \implies 1)$ Lo interesante es demostrar que 2. implica a 1., pues 2. parece una condición más débil. Así pues, supongamos que $X$ es una función que satisface 2.; que para cada $A \in \mathcal{G}$ se cumple que $X^{-1}[A] \in \mathscr{F}$. Ahora queremos demostrar que $X$ es una variable aleatoria. Es decir, queremos demostrar que para cada $B \in \mathscr{B}(\RR)$ se cumple que $X^{-1}[B] \in \mathscr{F}$.

Ahora, hay algunas propiedades importantes de la imagen inversa de una función. Por tus clases de álgebra superior, sabes que para cualquier colección $\{ B_{i} \}_{i \in \mathbb{N}^{+}}$ de subconjuntos de $\RR$ se cumple que

la imagen inversa «abre» la unión: \begin{align*} X^{-1}{\left[ \bigcup_{i=1}^{\infty} B_{i} \right]} = \bigcup_{i=1}^{\infty} X^{-1}{\left[ B_{i} \right]}, \end{align*}

la imagen inversa «abre» la intersección: \begin{align*} X^{-1}{\left[ \bigcap_{i=1}^{\infty} B_{i} \right]} = \bigcap_{i=1}^{\infty} X^{-1}{\left[ B_{i} \right]}. \end{align*}

y además, para cada $B \subseteq \RR$ se cumple que $X^{-1}[\RR \setminus B] = \Omega \setminus X^{-1}[B]$. Defínase ahora $\mathcal{M}$ como sigue:

\begin{align*} \mathcal{M} = \{\, B \subseteq \RR \mid X^{-1}[B] \in \mathscr{F} \,\}. \end{align*}

Es decir, los elementos de $\mathcal{M}$ son los subconjuntos de $\RR$ tales que $X^{-1}[B] \in \mathscr{F}$. Usando las propiedades de la imagen inversa bajo $X$, es posibe demostrar que $\mathcal{M}$ es un σ-álgebra. Más aún, sabemos que para cada $A \in \mathcal{G}$ se cumple que $X^{-1}[A] \in \mathscr{F}$. Por ende, $\mathcal{G} \subseteq \mathcal{M}$. Pero $\mathcal{M}$ es un σ-álgebra, y lo anterior demuestra que es un σ-álgebra que contiene a $\mathcal{G}$. En consecuencia, $\sigma(\mathcal{G}) \subseteq \mathcal{M}$.

¡Ajá! Pero $\sigma(\mathcal{G}) = \mathscr{B}(\RR)$; por lo que $\mathscr{B}(\RR) \subseteq \mathcal{M}$. Para concluir, sea $B \in \mathscr{B}(\RR)$. Por lo anterior, se sigue que $B \in \mathcal{M}$, que por la definición de $\mathcal{M}$ significa que $X^{-1}[B] \in \mathscr{F}$, que es justamente lo que queríamos demostrar.

$\square$

Este teorema es de mucha utilidad, ya que dada una función $X\colon\Omega\to\RR$, demostrar que $X$ es una variable aleatoria es equivalente a demostrar que $X$ preserva la medibilidad sobre una familia de conjuntos que genera a $\mathscr{B}(\RR)$, una tarea mucho más sencilla que hacerlo para todos los elementos del σ-álgebra de Borel.

Definición alternativa de variable aleatoria

Previamente establecimos que $\mathscr{B}(\RR)$ es el σ-álgebra generado por varias familias de subconjuntos de $\RR$. En particular, $\mathscr{B}(\RR)$ puede generarse a partir de la familia de intervalos de la forma $(-\infty, x]$, con $x \in \RR$. Por ello, gracias al teorema que demostramos, podemos caracterizar a una variable aleatoria como sigue:

Definición (alternativa). Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad. Diremos que una función $X\colon\Omega\to\RR$ es una variable aleatoria si para cada $x \in \RR$ se cumple que $X^{-1}[(-\infty, x]] \in \mathscr{F}$. Esto es,

\[ \{ \, \omega \in \Omega \mid X(\omega) \leq x \, \} \in \mathscr{F}. \]

La definición anterior es la que presentan algunos libros como la definición de variable aleatoria (por ejemplo, así la encontrarás el libro del Dr. Luis Rincón, si es que decides consultarlo). No temas, ambas maneras de definir el concepto de variable aleatoria son equivalentes, todo gracias al teorema que vimos en esta entrada.

Medida de probabilidad inducida por una variable aleatoria

Dados $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y $X\colon\Omega\to\RR$ una variable aleatoria, vimos que podíamos usar la medida de probabilidad $\mathbb{P}$ para medir la probabilidad de los subconjuntos de la forma $(-\infty, x]$ a través de sus imágenes inversas bajo $X$. De hecho, gracias a lo que discutimos al final de la sección pasada, resulta que esto se puede hacer para cualquier evento de $\RR$, es decir, para todos los elementos de $\mathscr{B}(\RR)$. A la medida resultante para los eventos de $\RR$ se le conoce como la medida de probabilidad inducida por $X$, y se define como sigue.

Definición. Sean $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y $X\colon\Omega\to\RR$ una variable aleatoria. La medida de probabilidad inducida por $X$ es la medida de probabilidad $P_{X}: \mathscr{B}(\RR) \to \RR$ dada por

\begin{align*} P_{X}(B) &= \Prob{\{\, \omega \in \Omega \mid X(\omega) \in B \,\}}, & \text{para cada $B \in \mathscr{B}(\RR)$. } \end{align*}

Equivalentemente, usando la notación probabilista para imágenes inversas, $P_{X}: \mathscr{B}(\RR) \to \RR$ es la función dada por

\begin{align*} P_{X}(B) &= \Prob{X \in B}, & \text{para cada $B \in \mathscr{B}(\RR)$}. \end{align*}

De este modo, si $(\Omega, \mathscr{F}, \mathbb{P})$ es un espacio de probabilidad y $X\colon\Omega\to\RR$ es una variable aleatoria, entonces $(\RR, \mathscr{B}(\RR), P_{X})$ es un espacio de probabilidad.

Ejemplos básicos de variables aleatorias

Ejemplo 1. Hay una gran cantidad de experimentos aleatorios cuyos resultados se reducen a «éxito» o «fracaso». Por ejemplo, en el lanzamiento de una moneda, el «águila» y el «sol» podrían verse como «éxito» y «fracaso», respectivamente. Comenzamos con el espacio muestral $\Omega = \{ \mathrm{«Exito», «Fracaso»} \}$. Definimos la variable aleatoria $X\colon\Omega\to\RR$ como sigue

\begin{array}{rcl} X(\mathrm{«Exito»}) & = & 1, \\ X(\mathrm{«Fracaso»}) & = & 0. \end{array}

La elección de estos dos números es un poco arbitraria, aunque obedece a la noción de que, en ciertos contextos, el $1$ es un «acierto» y el $0$ un «error». Esto pasa incluso en la lógica, en donde a veces se denota al «verdadero» como $1$ y al «falso» como $0$, sobre todo en contextos computacionales.

Como σ-álgebra tomaremos a $\mathscr{P}(\Omega)$ y como medida de probabilidad tomaremos la siguiente: sea $p \in \RR$ tal que $p \in [0,1]$. Definimos $\mathbb{P}\colon\mathscr{P}(\Omega)\to\RR$ como sigue:

\begin{array}{rcl} \Prob{\{\mathrm{«Exito»}\}} & = &p, \\ \Prob{\{\mathrm{«Fracaso»}\}} & = & 1 − p, \end{array}

\begin{array}{rcl} \Prob{\emptyset} & = & 0, \\ \Prob{\Omega} & = & p + (1 − p) = 1. \end{array}

En consecuencia, se tendrá que $\Prob{X = 1} = p$ y $\Prob{X = 0} = 1 − p$. De este modo, podemos ver que

\[ \Prob{X = x} = \begin{cases} p & \text{si $x = 1$}, \\ 1 − p & \text{si $x = 0$}, \\ 0 & \text{en otro caso}. \end{cases} \]

Esta es una variable aleatoria muy sencilla, pero muy poderosa. Más adelante, cuando ya hayamos visto más conceptos relacionados con variables aleatorias, la veremos con más detalle.

Ejemplo 2. Considera el experimento de lanzar un dado $2$ veces. El espacio muestral de este experimento es

\begin{align*} \Omega = \begin{Bmatrix} (1,1), & (1,2), & (1,3), & (1,4), & (1,5), & (1,6) \\ (2,1), & (2,2), & (2,3), & (2,4), & (2,5), & (2,6) \\ (3,1), & (3,2), & (3,3), & (3,4), & (3,5), & (3,6) \\ (4,1), & (4,2), & (4,3), & (4,4), & (4,5), & (4,6) \\ (5,1), & (5,2), & (5,3), & (5,4), & (5,5), & (5,6) \\ (6,1), & (6,2), & (6,3), & (6,4), & (6,5), & (6,6) \end{Bmatrix}, \end{align*}

tomando como σ-álgebra a $\mathscr{P}(\Omega)$ y con la medida de probabilidad clásica, $\Prob{A} = \frac{|A|}{|\Omega|}$, para cada $A \in \mathscr{P}(\Omega)$. Definimos la variable aleatoria $S\colon\Omega\to\RR$ de la siguiente manera: para cada $(\omega_{1}, \omega_{2}) \in \Omega$,

\[ S(\omega_{1}, \omega_{2}) = \omega_{1} + \omega_{2}. \]

Primero, observa que esto es algo que ya habíamos hecho antes, pero sin variables aleatorias: $S$ corresponde a la suma de los resultados de los dos lanzamientos de dado. Observa que los posibles valores que puede tomar esta variable aleatoria son los números naturales del $2$ al $12$. Por ejemplo, ¿cuál sera la probabilidad de $(S = 6)$? Para ello, veamos cuáles son los elementos de este evento.

\begin{align*} (S = 6) = \{\, (\omega_{1}, \omega_{2}) \in \Omega \mid S(\omega_{1}, \omega_{2}) = 6 \,\} &= \{\, (\omega_{1}, \omega_{2}) \in \Omega \mid \omega_{1} + \omega_{2} = 6 \,\} \\[0.5em] &= \{ (1,5), (2,4), (3,3), (4,2), (5,1) \}. \end{align*}

En consecuencia, tenemos que

\[ \Prob{S = 6} = \Prob{\{ (1,5), (2,4), (3,3), (4,2), (5,1) \}} = \frac{5}{36}. \]

Entonces la probabilidad de que la variable aleatoria tome el valor $6$ es de $\frac{5}{36} \approx 0.1389$.

De hecho, es posible establecer una fórmula para la probabilidad de cada resultado de este experimento. Nos quedaría como sigue:

\[ \Prob{S = s} = \begin{cases} \frac{6 – |s – 5|}{36} & \text{si $s \in \{2,3,4,5,6,7,8,9,10,11,12\}$}, \\[0.25em] 0 & \text{en otro caso}. \end{cases} \]

Observa que es necesario definir a $\Prob{S = s}$ como $0$ incluso cuando $s$ no es uno de los valores que puede tomar la variable aleatoria. Esto pasa porque los eventos de la forma $(S = s)$ están definidos para todos los $s \in \RR$, así que la probabilidad de estos eventos debe de definirse, incluso si es $0$. Por ejemplo, la probabilidad de que $(S = 7.34)$ es $0$, pues no es uno de los valores que puede tomar $S$.

Por otro lado, ¿cuál es la probabilidad de que $(S \leq 4)$? Hay que ver cuáles son los pares de lanzamientos que hacen que $S$ sea menor o igual que $4$:

\begin{align*} (S \leq 4) = \{\, (\omega_{1}, \omega_{2}) \in \Omega \mid S(\omega_{1}, \omega_{2}) \leq 4 \,\} &= \{\, (\omega_{1}, \omega_{2}) \in \Omega \mid \omega_{1} + \omega_{2} \leq 4 \,\} \\[0.5em] &= \{ (1,1), (1,2), (1,3), (2,1), (2,2), (3,1) \}. \end{align*}

En consecuencia se tiene que $\Prob{S \leq 4} = \frac{6}{36} = \frac{1}{6} \approx 0.1667$. Otra manera de hacerlo es sumar las probabilidades de que $S$ tome los valores menores o iguales a $4$, sobre aquellos valores que sí puede tomar. Esto es,

\begin{align*} \Prob{S \leq 4} = \sum_{k=2}^{4} \Prob{S = k} &= \Prob{S = 2} + \Prob{S = 3} + \Prob{S = 4} \\ &= \frac{1}{36} + \frac{2}{36} + \frac{3}{36} \\ &= \frac{6}{36} \\ &= \frac{1}{6} \end{align*}

Esto es algo que se cumple para aquellas variables aleatorias que pueden tomar a lo más una cantidad numerable de valores, como es el caso de $S$. Lo mismo pasa aún cuando el evento que nos interesa involucra a un valor que $S$ no puede tomar. Por ejemplo, $\Prob{S \leq 3.76}$ se puede calcular como

\[ \Prob{S \leq 3.76} = \Prob{S = 2} + \Prob{S = 3} = \frac{1}{36} + \frac{2}{36} = \frac{3}{36} = \frac{1}{12}, \]

pues los valores que puede tomar $S$ que son menores o iguales a $3.76$ son $2$ y $3$.

Las variables aleatorias de estos ejemplos son conocidas como discretas porque la cardinalidad del conjunto de valores que pueden tomar es finito. Más adelante veremos con propiedad lo que es una variable aleatoria discreta. Sin embargo, a pesar de que podemos definir muchos ejemplos de variables aleatorias con su regla de correspondencia, veremos más adelante que podemos prescindir por completo de esto. Así, lo único que importará es la probabilidad de los eventos de la forma $(X \leq x)$, sin necesidad de mencionar explícitamente a $\Omega$.

Tarea moral

De acuerdo con la notación probabilista adoptada en esta entrada, ¿cómo se escribe el evento $( X = 4 )$ sin usar la notación? ¿Y cómo se escribe $\{ \, \omega \in \Omega \mid X(\omega) = 3 \, \}$ utilizando la notación?
De acuerdo con la notación probabilista para eventos, ¿cómo se escribe el evento $(X < x)$ explícitamente (sin usar la notación)?
Verifica que $\mathcal{M}$, visto en la demostración del teorema de esta entrada, es un σ-álgebra.
En el Ejemplo 2:
1. Verifica que la fórmula que dimos para $\Prob{S = s}$ es correcta.
2. Calcula las probabilidades de que $(S < 6)$ y $(S \leq 5)$. ¿Qué puedes observar?

Más adelante…

Más adelante veremos que las variables aleatorias se pueden dividir en distintos tipos, dependiendo del tipo de conjunto de valores que pueden tomar. Además, en la siguiente entrada veremos que existen funciones que permiten capturar la probabilidad de cualquier evento asociado a una variable aleatoria $X$. De hecho, esto incluso nos permitirá omitir casi por completo al espacio muestral $\Omega$, y lo que importará será únicamente la probabilidad de los eventos asociados a $X$.

Por otro lado, en el contexto más general de la teoría de la medida, el concepto que definimos como variable aleatoria es conocido como función medible.

Entradas relacionadas

Ir a Probabilidad I
Entrada anterior del curso: Teorema de Continuidad de la Probabilidad
Siguiente entrada del curso: Funciones de Distribución de Probabilidad