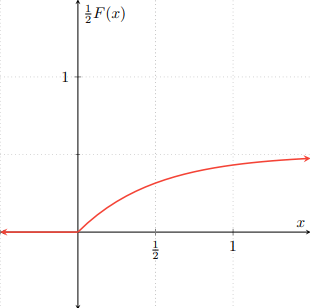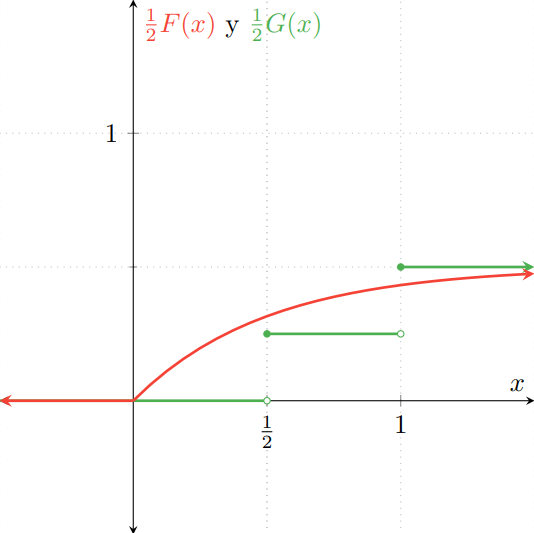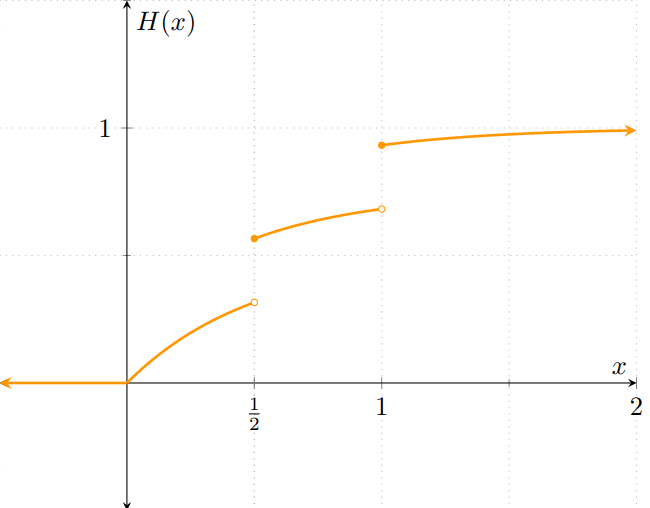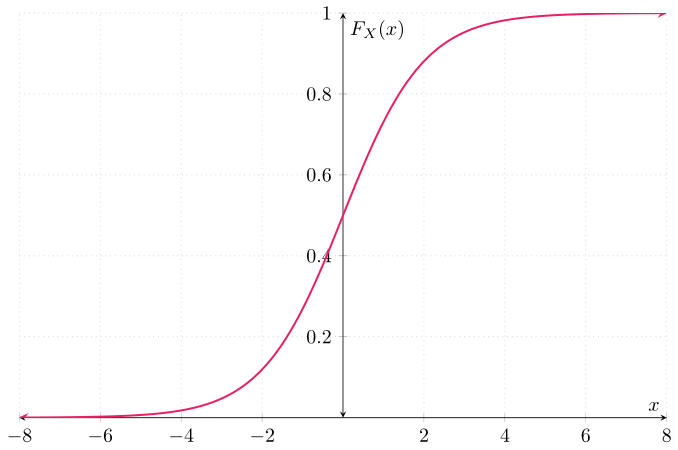Introducción
En las últimas entradas presentamos dos tipos muy importantes de v.a.’s que estudiaremos a lo largo del curso. No obstante, estos no son los únicos dos tipos de v.a.’s que existen, hay algunos tipos más. En particular, en esta entrada centraremos nuestra atención en las variables aleatorias mixtas. Estas son v.a.’s que no son ni discretas ni continuas, pero combinan propiedades de ambos tipos. Es decir, una v.a. mixta consta de una parte discreta y de una parte continua, que es la razón por la que reciben el nombre de mixta. Debido a que ya hemos estudiado ambos tipos de v.a.’s, podremos utilizar lo que hemos visto hasta ahora para describir a este nuevo tipo de v.a.’s.
Distribución mixta
Para comenzar, podemos ver una propiedad que ocurre al combinar dos funciones de distribución. Sean $F\colon\RR\to\RR$ y $G\colon\RR\to\RR$ dos funciones de distribución, y sea $\lambda\in[0,1]$. Definimos $H\colon\RR\to\RR$ como sigue:
\[ H(x) = \lambda F(x) + (1 − \lambda) G(x), \qquad \text{para cada $x \in \RR$.} \]
Es decir, para cada $x \in \RR$, $H(x)$ es una combinación lineal de $F(x)$ y $G(x)$. Más aún, como $\lambda$ es algún valor en $[0,1]$, se trata de una combinación convexa. Bien, ¡pues resulta que $H$ es una función de distribución! Te dejamos la comprobación de este hecho como tarea moral.
En particular, cuando $F$ y $G$ son funciones de distribución discretas, $H$ también es una función de distribución discreta. En cambio, cuando $F$ y $G$ son funciones de distribución absolutamente continuas, $H$ también es absolutamente continua.
Por otro lado, el tema principal de esta entrada surge cuando una de las dos distribuciones es discreta y la otra es continua. En tal caso, $H$ no es discreta ni continua, y es llamada una función de distribución mixta.
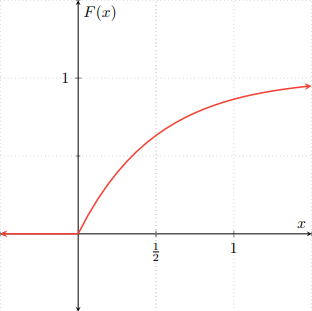
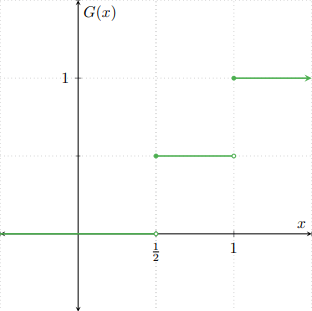
Ejemplo. Sean $F\colon\RR\to\RR$ y $G\colon\RR\to\RR$ las siguientes funciones de distribución.
\begin{align*}F(x) &= \begin{cases} 1 − e^{−2x} & \text{si $x \geq 0$,} \\[1em] 0 & \text{en otro caso,} \end{cases} & G(x) &= \begin{cases} 0 & \text{si $x < \frac{1}{2}$,} \\[1em] \dfrac{1}{2} & \text{si $\frac{1}{2} \leq x < 1$,} \\[1em] 1 & \text{si $x \geq 1$.}\end{cases} \end{align*}
Gráficamente, $F$ y $G$ se ven como sigue.
Definimos $H\colon\RR\to\RR$ como sigue.
\[ H(x) = \frac{1}{2}F(x) + \frac{1}{2}G(x) \qquad \text{para cada $x \in \RR$.} \]
Para visualizar un poco cómo se obtiene la gráfica de $H$, primero hay que multiplicar a $F$ y a $G$ por $\frac{1}{2}$, que nos da las siguientes gráficas:
Observa que se parecen mucho a las gráficas de las distribuciones $F$ y $G$, pero «aplastadas». El «aplastamiento» corresponde a que se han multiplicado por $\frac{1}{2}$. Al superponer ambas gráficas, obtenemos la siguiente figura:
Y en la gráfica de $H$, en el eje vertical tomará los valores $\frac{1}{2}F(x) + \frac{1}{2}G(x)$ para cada $x \in \RR$. La gráfica resultante es la siguiente:
Observa cómo la gráfica de $H$ es diferente a las que hemos visto en las últimas entradas: no es la función de distribución de una v.a. discreta porque no es una función escalonada, pero tampoco es la distribución de una v.a. continua porque presenta discontinuidades.
Sin embargo, ¡sí es una función de distribución! Es no-decreciente, continua por la derecha y sus límites a $-\infty$ e $\infty$ son $0$ y $1$, respectivamente. Por ello, sí es la función de distribución de alguna v.a… aún cuando esa v.a. no sea ni discreta ni continua.
De manera explícita, $H\colon\RR\to\RR$ es la función
\[ H(x) = \begin{cases} 0 & \text{si $x < 0$}, \\[1em] \dfrac{1 − e^{−2x}}{2} & \text{si $0 \leq x < \frac{1}{2}$}, \\[1em] \dfrac{1}{4} + \dfrac{1 − e^{−2x}}{2} & \text{si $\frac{1}{2} \leq x < 1$}, \\[1em] \dfrac{1}{2} + \dfrac{1 − e^{−2x}}{2} & \text{si $x \geq 1$}, \end{cases} \]
Sea $X$ una v.a. aleatoria con distribución $H$. Es decir, $X$ es una v.a. cuya función de distribución es $H$. Hay algunos aspectos interesantes que tiene una v.a. con esta distribución. Primero, los puntos de discontinuidad de $H$ son aquellos puntos con masa de probabilidad mayor a $0$. Observa que
\[ \Prob{X = \frac{1}{2}} = H{\left(\frac{1}{2}\right)} − H{\left(\frac{1}{2}−\right)} \]
Ahora, hay que tener cuidado con $H{\left(\frac{1}{2}−\right)}$. Para obtener este valor, hay que ver cómo se comporta $H(x)$ cuando $x \to \frac{1}{2}$ por la izquierda. Como $x$ se acerca por la izquierda a $\frac{1}{2}$, necesariamente el valor de $x$ es menor a $\frac{1}{2}$, así que $H(x) = \dfrac{1 − e^{−2x}}{2}$. Así, tenemos que
\[ H{\left(\frac{1}{2}−\right)} = \lim_{x\to{\frac{1}{2}}^{-}} H(x) = \lim_{x\to{\frac{1}{2}}^{-}} \dfrac{1 − e^{−2x}}{2} = \dfrac{1 − e^{−2{\left( \frac{1}{2} \right)}}}{2} = \dfrac{1 − e^{−1}}{2}. \]
Este límite fue fácil de evaluar porque la expresión de $H$ para $x < \frac{1}{2}$ describe una función continua. Es decir, $H(x)$ se acerca al valor $\dfrac{1 − e^{−1}}{2}$ cuando $x$ se acerca a $\frac{1}{2}$ por la izquierda. Aún cuando $H$ brinca en ese punto, el límite por la izquierda corresponde al lugar donde se encuentra el hoyito en la gráfica.
En consecuencia, tenemos que
\[ \Prob{X = \frac{1}{2}} = \frac{1}{4} + \dfrac{1 − e^{−1}}{2} − {\left(\dfrac{1 − e^{−1}}{2}\right)} = \frac{1}{4}. \]
De manera similar podemos obtener que
\[ \Prob{X = 1} = \frac{1}{2} + \dfrac{1 − e^{−2}}{2} − {\frac{1}{4} + \left(\dfrac{1 − e^{−2}}{2}\right)} = \frac{1}{4}, \]
por lo que hay dos puntos que tienen masa de probabilidad mayor a $0$. Esto es algo que no pasa en las v.a.’s absolutamente continuas. Debido a esto, cuando se trata de v.a.’s mixtas, hay que tener cuidado en el cálculo de probabilidades de algunos eventos. Por ejemplo,
\[ \Prob{X \leq \frac{1}{2}} = H{\left(\frac{1}{2}\right)} = \frac{1}{4} + \dfrac{1 − e^{−1}}{2}, \]
pero por otro lado,
\[ \Prob{X < \frac{1}{2}} = H{\left(\frac{1}{2}\right)} − \Prob{X = \frac{1}{2}} = \frac{1}{4} + \dfrac{1 − e^{−1}}{2} − \frac{1}{4} = \dfrac{1 − e^{−1}}{2}. \]
En consecuencia, existe $a \in \RR$ tal que $\Prob{X \leq a} \neq \Prob{X < a}$, que es algo que pasa en las v.a.’s discretas. Esos puntos son precisamente los puntos en los que la función de distribución presenta una discontinuidad, por lo que hay que tener cuidado cuando una desigualdad involucra a uno de estos puntos. En consecuencia, también se debe de tener cuidado al obtener la probabilidad de intervalos de la forma $(a,b)$, $[a,b]$, $(a,b]$, etcétera, cuando $a$ y $b$ son puntos en los que la distribución presenta una discontinuidad.
Otra manera de obtener variables aleatorias mixtas
Además de hacer combinaciones lineales de funciones de distribución, también es posible obtener v.a.’s mixtas a partir de v.a.’s continuas. Sea $X\colon\Omega\to\RR$ una v.a. continua, y sea $c \in \RR$ una constante tal que $0 < F_{X}(c) < 1$ (esto es, la distribución de $X$ evaluada en $c$ es mayor a $0$ y menor a $1$). Definimos las variables aleatorias $U\colon\Omega\to\RR$ y $L\colon\Omega\to\RR$ como sigue:
\begin{align*} U(\omega) &= \max{\left\lbrace X(\omega), c \right\rbrace} \qquad \text{para cada $\omega \in \Omega$}, \\[1em] L(\omega) &= \min{\left\lbrace X(\omega), c \right\rbrace} \qquad \text{para cada $\omega \in \Omega$}. \end{align*}
Resulta que estas v.a.’s son ejemplos de variables aleatorias mixtas. Veamos que $U$ lo es. Para ello, hay que analizar dos subconjuntos importantes del espacio muestral sobre el que está definida $X$. Estos son:
\begin{align*} A_{1} &= \{ \, \omega \in \Omega \mid X(\omega) \leq c \, \} & A_{2} &= \{ \,\omega \in \Omega \mid X(\omega) > c \, \}\end{align*}
La razón por la que hemos escogido estos conjuntos se basa en el valor que toma $U(\omega)$ dependiendo de si $X(\omega) \leq c$ o $X(\omega) > c$. Cuando $X(\omega) \leq c$, se tiene que
\[ U(\omega) = \max{\left\lbrace X(\omega), c \right\rbrace} = c, \]
al ser $c$ el mayor de los dos valores. En consecuencia, por la manera en que hemos definido a $A_{1}$, para cada $\omega \in A_{1}$ se cumple que $U(\omega) = c$. Esto significa que
\[ \Prob{U = c} = \Prob{A_{1}} = \Prob{\{ \, \omega \in \Omega \mid X(\omega) \leq c \, \}} = \Prob{X \leq c} = F_{X}(c), \]
y como $c$ cumple que $0 < F_{X}(c) < 1$, se tiene que
\[ \Prob{U = c} > 0, \]
por lo que $U$ tiene al menos un punto con masa de probabilidad mayor a cero. Esto nos indica que $U$ al menos cuenta con una parte discreta, algo que $X$ no tenía.
Por otro lado, para $\omega \in\Omega$ tal que $X(\omega) > c$, se tiene que
\[ U(\omega) = \max{\left\lbrace X(\omega), c \right\rbrace} = X(\omega). \]
Por consiguiente, para cada $\omega \in A_{2}$ se tiene que $U(\omega) = X(\omega)$. Ahora, nota que para cada $x \in [c,\infty)$ se cumple que
\[ \{ \, \omega \in \Omega \mid X(\omega) > x \, \} \subseteq A_{2} \]
pues si $\omega \in \Omega$ satisface $X(\omega) > x$, como $x \in [c,\infty)$, se tiene que $x \geq c$, y por lo tanto, $X(\omega) > c$. Luego, $\omega \in A_{2}$. Por tanto, para $x \in [c, \infty)$ se cumple $\Prob{X > x} = \Prob{U > x}$, pues $X(\omega) = U(\omega)$ en cada uno de los $\omega \in (X > x)$. Así, para cada $x \in [c,\infty)$ se tiene que
\begin{align*} \Prob{X > x} = \Prob{U > x} &\iff 1 − \Prob{X \leq x} = 1 − \Prob{U \leq x} \\[1em] &\iff − \Prob{X \leq x} = − \Prob{U \leq x} \\[1em] &\iff \Prob{X \leq x} = \Prob{U \leq x} \\[1em] &\iff F_{X}(x) = F_{U}(x), \end{align*}
es decir, $X$ y $U$ tienen la misma función de distribución sobre conjunto $[c, \infty)$. Esto garantiza que, sobre $[c, \infty)$, la función de distribución de $U$ es una función absolutamente continua. Sin embargo, hay un detalle importante que necesitamos para asegurarnos de que $U$ es una v.a. mixta. Observa que como pedimos que $F_{X}(c) < 1$, se tiene que $0 < 1 − F_{X}(c)$, y como $F_{X}(c) = F_{U}(c)$, esto garantiza que $0 < 1 − F_{U}(c)$. En conclusión, $\Prob{U > c} > 0$, garantizando que $U$ no es una v.a. exclusivamente discreta.
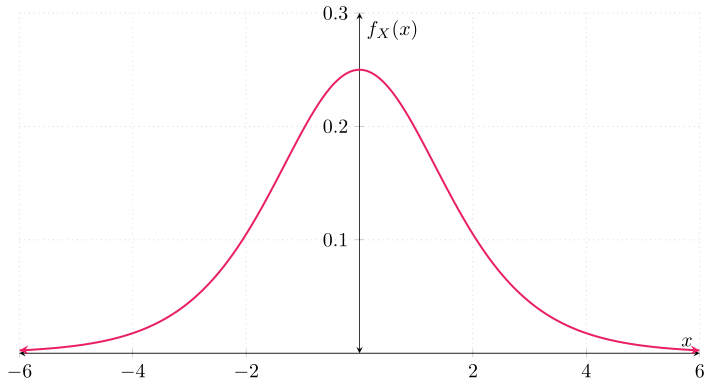
Ejemplo. Sea $X\colon\Omega\to\RR$ una v.a. con función de densidad $f_{X}\colon\RR\to\RR$ dada por
\begin{align*} f_{X}(x) &= \frac{e^{-x}}{(1 + e^{-x})^{2}} & \text{para cada $x \in \RR$}, \end{align*}
y sea $U\colon\Omega\to\RR$ la v.a. dada por
\begin{align*} U(\omega) &= \max{\left\lbrace X(\omega), 0 \right\rbrace} & \text{para cada $\omega \in \Omega$}. \end{align*}
Cuando una v.a. tiene esta función de densidad, se dice que sigue una distribución logística. Ahora, ¿cuál es la función de distribución de $U$? Para obtenerla, primero obtengamos la función de distribución de $X$, $F_{X}$. Conocemos la función de densidad de $X$. Gráficamente:
Así que podemos obtener la distribución de $X$ a partir de esta. Así, para cada $x \in \RR$ tenemos que
\begin{align} \label{eq:dist1} F_{X}(x) = \int_{-\infty}^{x} f_{X}(t) \,\mathrm{d}t = \int_{-\infty}^{x} \frac{e^{-t}}{(1 + e^{-t})^{2}} \,\mathrm{d}t. \end{align}
Mediante una sustitución de variables, podemos obtener que la primitiva de $f_{X}$ que satisface lo anterior es
\begin{align} \label{eq:dist2} F_{X}(x) &= \frac{1}{1 + e^{-x}} & \text{para cada $x\in\RR$}. \end{align}
Es decir, esta es la función de distribución de $X$. Gráficamente:
Ahora, para obtener la función de distribución de $U$, hay que ver varios casos. Sea $u \in \RR$ tal que $u < 0$. Para este caso, tenemos que
\[ F_{U}(u) = \Prob{U \leq u} = \Prob{\max\{X, 0\} \leq u}. \]
Sin embargo, como $u < 0$ y $\max\{X, 0\} \geq 0$, el evento $(\max\{X,0\} \leq u) = \emptyset$, pues
\[ (U \leq u) = (\max\{X,0\} \leq u) = \{\, \omega \in \Omega \mid \max\{X(\omega), 0\} \leq u \,\}, \]
y para que exista algún $\omega \in (U \leq u)$, debe de cumplirse que $\max\{X(\omega), 0\} \leq u < 0$, lo cual es imposible. En consecuencia, se tiene que
\begin{align*} F_{U}(u) &= 0 & \text{para $u < 0$}. \end{align*}
Por otro lado, para $u = 0$, tenemos que
\[ F_{U}(u) = \Prob{U \leq 0} = \Prob{U = 0} + \Prob{U < 0} = \Prob{U = 0}. \]
Por su parte, $\Prob{U = 0} = \Prob{\max\{X, 0\} = 0}$, así que hay que recurrir a la distribución de $X$ para obtener este valor. Así,
\begin{align*} \Prob{\max\{X, 0\} = 0} &= \Prob{\{\, \omega \in \Omega \mid \max\{X(\omega), 0\}} = 0 \,\} \\[1em] &= \Prob{\{\, \omega \in \Omega \mid X(\omega) \leq 0 \,\}} \\[1em] &= \Prob{X \leq 0} \\[1em] &= F_{X}(0) \\[1em] &= \frac{1}{1 + e^{-(0)}} \\[1em] &= \frac{1}{1 + 1} \\[1em] &= \frac{1}{2}. \end{align*}
De este modo, $F_{U}(0) = \frac{1}{2}$. Así, tenemos que
\[ F_{U}(u) = \begin{cases} 0 & \text{si $u < 0$}, \\[1em] \frac{1}{2} & \text{si $u = 0$}. \end{cases} \]
Finalmente, para $u > 0$, ya vimos (en el caso general) que
\[ F_{U}(u) = F_{X}(u) = \frac{1}{1 + e^{-u}}\]
por lo que la función de distribución de $U$ queda como
\[ F_{U}(u) = \begin{cases} 0 & \text{si $u < 0$}, \\[1em] \dfrac{1}{2} & \text{si $u = 0$}, \\[1em] \dfrac{1}{1 + e^{-u}} & \text{si $u > 0$}.\end{cases} \]
Gráficamente, la función de distribución de $U$ se ve así:
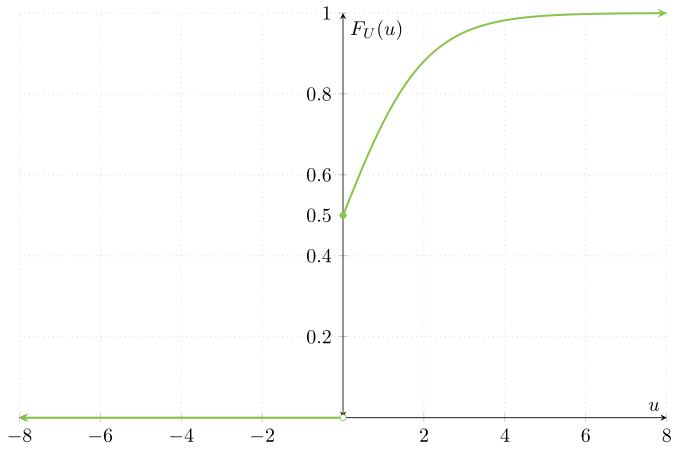
Observa que la función de distribución de $U$ es precisamente la de $X$, pero truncada. De hecho, como comentamos previamente, para cada $x \geq 0$ se cumple que $F_{U}(x) = F_{X}(x)$. Sin embargo, la función de distribución de $U$ es $0$ para cada $x<0$, pues $U$ no toma valores menores a $0$.
Tarea moral
Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.
- Sean $F\colon\RR\to\RR$ y $G\colon\RR\to\RR$ dos funciones de distribución. Demuestra que para cualquier $\lambda\in [0,1]$, la función $H\colon\RR\to\RR$ dada por\[ H(x) = \lambda F(x) + (1 − \lambda) G(x), \qquad \text{para cada $x \in \RR$,} \]es una función de distribución.
- Sean $X\colon\Omega\to\RR$ una v.a. continua y $c \in \RR$ tal que $0 < F_{X}(c) < 1$. Sea $L\colon\Omega\to\RR$ la v.a. dada por\[ L(\omega) = \min{\left\lbrace X(\omega), c \right\rbrace} \qquad \text{para cada $\omega \in \Omega$}. \]Verifica que $L$ es una v.a. mixta.
- Al definir las v.a.’s del máximo y el mínimo, ¿qué pasa si $F_{X}(c) = 0$ o $F_{X}(c) = 1$? Por ejemplo, toma $X$ una v.a. con distribución exponencial (vista en la entrada pasada), y toma $c = -5$. ¿Qué pasa con las v.a.’s $U = \max{\{ X, c \}}$ y con $L = \min{\{X, c \}}$?
- Verifica que la función de distribución dada por \eqref{eq:dist2} es la función que satisface la ecuación \eqref{eq:dist1}.
Más adelante…
Las v.a.’s aleatorias mixtas llegan a hacerse presentes en algunas aplicaciones financieras y estadísticas. En el análisis de supervivencia (correspondiente a la materia de Estadística III, o Modelos de Supervivencia y Series de Tiempo) hay modelos que hacen uso de transformaciones de v.a.’s como el mínimo, dando como resultado v.a.’s mixtas.
Existe un tipo adicional de v.a.’s que no hemos mencionado hasta el momento, que son las variables aleatorias singulares. Cerca del final del curso haremos una mención a este último tipo de v.a.’s, cuando hayamos definido la noción de «convergencia en distribución». Con ello, presentaremos el bosquejo de un ejemplo de una v.a. cuya distribución es singular.
En la siguiente entrada abordaremos el tema de obtener la distribución de funciones de v.a.’s aleatorias, que no será otra cosa que hacer una composición de funciones.
Entradas relacionadas
- Ir a Probabilidad I
- Entrada anterior del curso: Variables Aleatorias Continuas
- Siguiente entrada del curso: Transformaciones de Variables Aleatorias