Introducción
En la entrada pasada vimos el último tipo importante de v.a. que veremos, por ahora: las v.a.’s mixtas. En particular, vimos una manera de construir v.a.’s mixtas siguiendo un método muy sencillo: evaluando el $\max$ y el $\min$ en alguna v.a. continua. Esto puede pensarse como «transformar» la v.a. continua dada mediante las funciones $\max$ y $\min$. No sólamente la transformación fue posible, sino que además la función resultante es una v.a., y obtuvimos su función de distribución. Este proceso puede generalizarse para obtener la distribución de muchas más funciones de v.a.’s continuas.
Composición de funciones y variables aleatorias
Una de las cosas que hicimos en la entrada pasada fue ver que, dada una v.a. continua $X$, podíamos obtener v.a.’s mixtas a partir de $X$. Vamos a refinar un poco lo que hicimos en la entrada pasada. Sea $c\in\RR$, y sea $\mathrm{max}_{c}\colon\RR\to\RR$ la función dada por
\begin{align*} \mathrm{max}_{c}(x) &= \max{\left\lbrace x, c \right\rbrace}, & \text{para cada $x\in\RR$.} \end{align*}
De este modo, definimos una v.a. nueva $U$ como $U = \mathrm{max}_{c}(X)$. Sin embargo, ¿qué es exactamente «$\mathrm{max}_{c}(X)$»? Sabemos que $X$ es una «variable aleatoria», lo que significa que $U$ es como «evaluar» una función en una variable aleatoria. No obstante, esto no es otra cosa que… ¡una composición de funciones! Como recordatorio de Álgebra Superior I, dadas funciones $f\colon A\to B$, $g\colon B\to C$, la composición $g \circ f \colon A \to C$, llamada $f$ seguida de $g$, se define como
\begin{align*} g \circ f (x) &= g(f(x)), & \text{para cada $x\in A$.} \end{align*}
Recordando la definición de variable aleatoria, cuando tenemos un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$ sabemos que una función $X\colon\Omega\to\RR$ es una variable aleatoria si satisface una condición de «medibilidad», que dimos hace unas entradas. De momento, lo que más nos importa es que una v.a. es una función. En consecuencia, la v.a. $U$ que definimos no es otra cosa que $\mathrm{max}_{c} \circ X\colon\Omega\to\RR$, dada por
\begin{align*} \mathrm{max}_{c} \circ X (\omega) &= \max{\{ X(\omega), c \}}, & \text{para cada $x \in \Omega$}, \end{align*}
que es justamente como la definimos en la entrada anterior a esta. Ahora bien, dadas una v.a. $X\colon\Omega\to\RR$ y una función $g\colon\RR\to\RR$, hay que tener cuidado con $g$ para que $g \circ X$ sea una v.a., pues puede pasar que la función resultante no es una variable aleatoria, de acuerdo con la definición. Nosotros nos abstendremos de presentar casos degenerados de ese estilo, pero expondremos las condiciones que se necesitan para que una transformación de una v.a. sea nuevamente una v.a.
¿Cuáles funciones sí dan como resultado variables aleatorias?
Comenzaremos con una definición general del tipo de funciones que nos serán útiles.
Definición. Si $g\colon\RR\to\RR$ es una función, diremos que $g$ es una función Borel-medible si para cada $B \in \mathscr{B}(\RR)$ se cumple que $g^{-1}(B) \in \mathscr{B}(\RR)$.
Es decir, $g$ es una función Borel-medible si la imagen inversa de cualquier elemento del σ-álgebra de Borel es también un elemento del σ-álgebra de Borel.
Si recuerdas la definición de variable aleatoria, podrás observar que… ¡Es casi la misma! En realidad, ambas son el mismo concepto en la teoría más general: son funciones medibles. En particular, las funciones Borel-medibles reciben su nombre por el σ-álgebra que preservan: el σ-álgebra de Borel. De hecho, observa que las funciones Borel-medibles son un caso particular de nuestra definición de variable aleatoria, usando $(\RR, \mathscr{B}(\RR), \mathbb{P})$ como espacio de probabilidad. Por ello, todos los resultamos que hemos visto hasta ahora para v.a.’s aplican para funciones Borel-medibles.
Resulta que esta clase de funciones son aquellas que, al componer con una v.a., nos devuelven otra variable aleatoria.
Proposición. Sean $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad, $X\colon\Omega\to\RR$ una v.a. y $g\colon\RR\to\RR$ una función Borel-medible. Entonces $g \circ X \colon\Omega\to\RR$ es una variable aleatoria.
Demostración. Queremos demostrar que $g \circ X$ es una variable aleatoria. Es decir, que para cada $A \in \mathscr{B}(\RR)$ se cumple que $(g \circ X)^{-1}[A] \in \mathscr{F}$. Ahora, $(g \circ X)^{-1}[A] = X^{-1}[g^{-1}[A]]$, por propiedades de la imagen inversa. En consecuencia, hay que ver que para cada $A \in \mathscr{B}(\RR)$ se cumple que $X^{-1}[g^{-1}[A]] \in \mathscr{F}$.
Sea $A \in \mathscr{B}(\RR)$. Como $g$ es una función Borel-medible, esto implica que $g^{-1}[A] \in \mathscr{B}(\RR)$. Ahora, como $X$ es una variable aleatoria, $g^{-1}[A] \in \mathscr{B}(\RR)$ implica $X^{-1}[g^{-1}[A]] \in \mathscr{F}$, que es justamente lo que queríamos demostrar.
$\square$
Así, si $g\colon\RR\to\RR$ es una función Borel-medible y $X\colon\Omega\to\RR$ es una variable aleatoria, entonces $g \circ X$ es también una variable aleatoria.
Pero entonces, ¿qué funciones podemos usar?
A pesar de que lo anterior nos da muchas funciones con las cuales transformar v.a.’s, de momento quizás no conozcas ninguna función Borel-medible. No temas, el siguiente teorema nos da una gran cantidad de funciones que son Borel-medibles, y con las cuales seguramente te has encontrado antes.
Proposición. Si $g\colon\RR\to\RR$ es una función continua, entonces es Borel-medible.
Demostración. Sea $g\colon\RR\to\RR$ una función continua. Queremos demostrar que $g$ es Borel-medible. Es decir, que para cada $x \in \RR$, $X^{-1}[(-\infty, x)] \in \mathscr{B}(\RR)$.
Sea $x\in\RR$. Como $(-\infty, x)$ es un intervalo abierto, es un subconjunto abierto (en la topología usual) de $\RR$. En consecuencia, como $g$ es continua, $g^{-1}[(-\infty, x)]$ también es un subconjunto abierto de $\RR$.
Ahora, como $g^{-1}[(-\infty, x)]$ es un abierto, esto implica que existe una familia numerable de intervalos abiertos $\{ I_{n} \}_{n=1}^{\infty}$ tales que
\[ g^{-1}[(-\infty, x)] = \bigcup_{n=1}^{\infty} I_{n}. \]
Nota que como $I_{n}$ es un intervalo abierto, para cada $n \in \mathbb{N}^{+}$, entonces $I_{n} \in \mathscr{B}(\RR)$. Por lo tanto, $\bigcup_{n=1}^{\infty} I_{n} \in \mathscr{B}(\RR)$, que implica $g^{-1}[(-\infty, x)] \in \mathscr{B}(\RR)$, que es justamente lo que queríamos demostrar.
$\square$
Es muy probable que estés cursando Cálculo Diferencial e Integral III al mismo tiempo que esta materia, por lo que quizás no hayas visto algunos detalles de la topología usual de $\RR$ que utilizamos en la demostración anterior. Puedes consultar nuestras notas de Cálculo Diferencial e Integral III sobre el tema si lo consideras necesario.
Con esta última proposición hemos encontrado una gran cantidad de funciones válidas para transformar v.a.’s. Seguramente conoces muchísimas funciones continuas: los polinomios, funciones lineales, algunas funciones trigonométricas (como $\sin$ y $\cos$), etcétera.
Un primer método para obtener la distribución de una transformación
Una vez que conocemos muchas funciones con las cuales podemos transformar v.a.’s, nuestro objetivo es encontrar la distribución de tales transformaciones. Si $g\colon\RR\to\RR$ es una función Borel-medible y $X\colon\Omega\to\RR$ es una v.a. (cuya función de distribución es conocida), queremos encontrar la distribución de $Y = g \circ X$. Para hacerlo, basta con encontrar la probabilidad de los eventos de la forma
\begin{align*} (Y \leq y) = (g \circ X \leq y) = \{ \, \omega \in \Omega \mid g(X(\omega)) \leq y \, \}. \end{align*}
Es común encontrar la notación $g(X) = g \circ X$, y de este modo, se usa $(g(X) \leq y)$ para referirse a los eventos $(g \circ X \leq y)$.
Sin embargo, el caso de las v.a.’s discretas puede ser más sencillo, ya que la función de masa de probabilidad caracteriza el comportamiento de ese tipo de v’a’s. Veamos cómo hacerlo mediante el siguiente ejemplo.
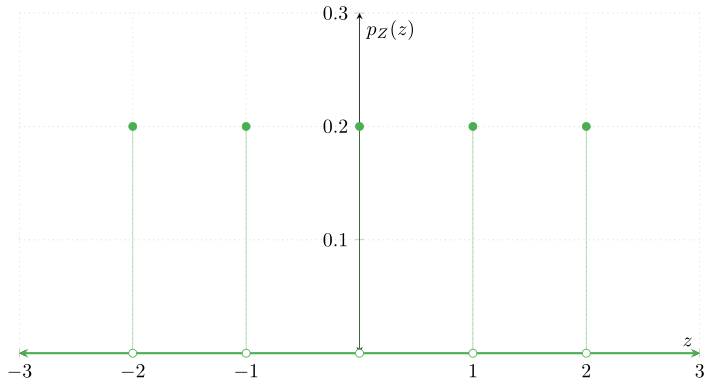
Ejemplo. Sea $Z$ una v.a. con función de masa de probabilidad $p_{Z}\colon\RR\to\RR$ dada por
\begin{align*} p_{Z}(z) = \begin{cases} \dfrac{1}{5} & \text{si $z \in \{-2, -1, 0, 1, 2 \}$}, \\[1em] 0 & \text{en otro caso}. \end{cases}\end{align*}
Ahora, sea $g\colon\RR\to\RR$ la función dada por
\begin{align*} g(x) &= x^{2} & \text{para cada $x \in \RR$.} \end{align*}
Defínase $Y = g (Z)$, es decir, $Y = Z^{2}$. Primero, el conjunto de posibles valores que puede tomar $Y$ es
\[ \{\, z^2 \mid z \in \textrm{Im}(Z) \,\} = \{ (-2)^{2}, (-1)^{2}, 0^{2}, 1^{2}, 2^{2} \} = \{ 4, 1, 0, 1, 4 \} = \{ 0, 1, 4 \}. \]
Observa que $Y$ puede tomar $3$ valores distintos, mientras que $Z$ puede tomar $5$. Ya desde este momento se nota que las probabilidades de los eventos que involucran a $Y$ van a ser distintas a los de $Z$.
Sea $y \in \RR$. Para obtener la función de masa de probabilidad de $Y$ tenemos que obtener la probabilidad de los eventos de la forma $(Y = y)$. Este evento es
\[ (Y = y) = \{\,\omega\in\Omega\mid Y(\omega) = y \,\}, \]
Es decir, $\omega\in (Y=y) \iff Y(\omega) = y$. Usando la definición de $Y$, se tiene que
\begin{align*} \omega\in (Y = y) &\iff Y(\omega) = y \\[1em] &\iff (g \circ Z)(\omega) = y \\[1em] &\iff g(Z(\omega)) = y \\[1em] &\iff (Z(\omega))^{2} = y \\[1em] &\iff {\left|Z(\omega)\right|} = \sqrt{y} \\[1em] &\iff (Z(\omega) = \sqrt{y} \lor Z(\omega) = -\sqrt{y}), \end{align*}
esto es, $\omega$ es un elemento de $(Y=y)$ si y sólamente si $Z(\omega) = \sqrt{y}$ o $Z(\omega) = -\sqrt{y}$. Esto es equivalente a que $\omega \in (Z = \sqrt{y}) \cup (Z = -\sqrt{y})$, por lo que podemos concluir que
\[ (Y = y) = (Z = \sqrt{y}) \cup (Z = -\sqrt{y}). \]
En consecuencia, $\Prob{Y = y} = \Prob{(Z = \sqrt{y}) \cup (Z = -\sqrt{y})}$, y así:
\[ \Prob{Y = y} = \Prob{Z = \sqrt{y}} + \Prob{Z = -\sqrt{y}}. \]
Para $y < 0$, observa que
\[ (Z = \sqrt{y}) = \{\,\omega\in\Omega\mid Z(\omega) = \sqrt{y} \,\} = \emptyset, \]
pues $Z$ toma valores en los reales, no en los complejos. Del mismo modo, cuando $y < 0$, $(Z = -\sqrt{y}) = \emptyset$; y así,
\begin{align*} \Prob{Y = y} &= \Prob{Z = \sqrt{y}} + \Prob{Z = -\sqrt{y}} = 0, & \text{para $y < 0$.} \end{align*}
Por otro lado, para $y \geq 0$, sólamente hay $3$ valores que importan: $0$, $1$ y $4$, como acordamos previamente. Para el caso de $y = 0$, observa que $(Z = \sqrt{0}) \cup (Z = -\sqrt{0}) = (Z = 0)$, pues
\begin{align*} \omega \in (Z = \sqrt{0}) \cup (Z = -\sqrt{0}) &\iff (Z(\omega) = \sqrt{0} \lor Z(\omega) = -\sqrt{0}) \\[1em] &\iff (Z(\omega) = 0 \lor Z(\omega) = 0) \\[1em] &\iff Z(\omega) = 0 \\[1em] &\iff \omega \in (Z = 0). \end{align*}
Por lo tanto, se tiene que
\begin{align*}
\Prob{Y = 0} &= \Prob{Z = 0} = \frac{1}{5}.
\end{align*}
Para $y = 1$ y $y = 4$ sí podemos aplicar la fórmula que obtuvimos:
\begin{align*} \Prob{Y = 1} &= \Prob{Z = \sqrt{1}} + \Prob{Z = -\sqrt{1}} = \Prob{Z = 1} + \Prob{Z = -1} = \frac{1}{5} + \frac{1}{5} = \frac{2}{5}, \\[1em] \Prob{Y = 4} &= \Prob{Z = \sqrt{4}} + \Prob{Z = -\sqrt{4}} = \Prob{Z = 2} + \Prob{Z = -2} = \frac{1}{5} + \frac{1}{5} = \frac{2}{5}. \end{align*}
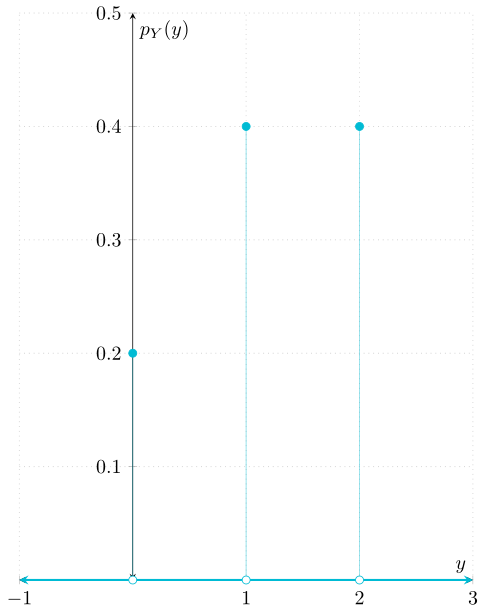
En conclusión, la función de masa de probabilidad de $Y$ es la función $p_{Y}\colon\RR\to\RR$ dada por
\begin{align*} p_{Y}(y) &= \begin{cases} \dfrac{1}{5} & \text{si $y = 0$,} \\[1em] \dfrac{2}{5} & \text{si $y = 1$ o $y = 4$,} \\[1em] 0 &\text{en otro caso.} \end{cases} \end{align*}
El ejemplo anterior ilustra lo que se debe de hacer para obtener las probabilidades de la transformación de una v.a. discreta. Sea $X\colon\Omega\to\RR$ una v.a. y sea $g\colon\RR\to\RR$ una función Borel-medible. Para cada $A \in \mathscr{B}(\RR)$, sabemos que el evento $(X \in A)$ no es otra cosa que $X^{-1}[A]$. Definimos la v.a. $Y$ como $Y = g(X)$. Ahora, sabemos que para cada $\omega\in\Omega$ se cumple que
\[ \omega \in X^{-1}[A] \iff X(\omega) \in A, \]
por la definición de imagen inversa. En consecuencia, para $(Y \in A)$ tenemos que
\begin{align*} \omega \in (Y \in A) &\iff \omega \in (g(X) \in A) \\[1em] &\iff g(X(\omega)) \in A \\[1em] &\iff X(\omega) \in g^{-1}[A] \\[1em] &\iff \omega \in (X \in g^{-1}[A]). \end{align*}
Por lo que $(Y \in A) = (X \in g^{-1}[A])$. Por ello, $\Prob{Y \in A} = \Prob{X \in g^{-1}[A]}$. Esto tiene sentido: como $Y = g(X)$, entonces la probabilidad de que $g(X)$ tome algún valor en $A$ es la misma que la probabilidad de que $X$ tome algún valor en $g^{-1}[A]$, pues todos los elementos de $g^{-1}[A]$ son mandados a $A$ cuando se les aplica $g$.
Finalmente, utilizando que $X$ es una v.a. discreta, tendremos que
\begin{align}\label{transf:1} \Prob{Y \in A} = \sum_{x \in g^{-1}[A]} \Prob{X = x}. \end{align}
En el caso particular en el que existe $y \in \RR$ tal que $A = \{ y \}$, tendremos que
\begin{align}\label{transf:2} \Prob{Y = y} = \sum_{x \in g^{-1}[\{ y\}]} \Prob{X = x}, \end{align}
justamente como hicimos en el ejemplo anterior. A continuación presentamos otro ejemplo siguiendo la misma metodología.
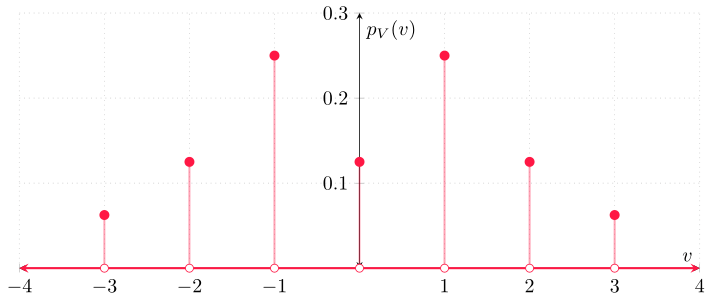
Ejemplo. Sea $V$ una v.a. con función de masa de probabilidad $p_{V}\colon\RR\to\RR$ dada por
\begin{align*} p_{V}(v) = \begin{cases} \dfrac{1}{2^{|v|+1}} & \text{si $v \in \{-3,-2,-1,1,2,3\}$}, \\[1em] \dfrac{1}{16} & \text{si $v = 0$}, \\[1em] 0 & \text{en otro caso}. \end{cases} \end{align*}
Nuevamente, considera la transformación $g\colon\RR\to\RR$ dada por $g(x) = x^{2}$ para cada $x \in \RR$. De este modo, defínase la v.a. $T$ como $T = g(V)$. Antes que nada, el conjunto de valores que puede tomar $T$ es el resultado de transformar el conjunto de los valores que puede tomar $V$. Si $\mathrm{Supp}(V) = \{-3,-2,-1,0,1,2,3\}$ es el conjunto de valores que puede tomar $V$, entonces el conjunto de valores que puede tomar $T$ es
\[ g{\left( \mathrm{Supp}(V) \right)} = \{ \, t \in \RR \mid \exists v \in \mathrm{Supp}(V)\colon g(v) = t \, \} = \{0, 1, 4, 9 \}. \]
Como $g$ es la misma transformación que en el ejemplo anterior, hay algunas cosas que ya sabemos. Primero,
\begin{align*} \Prob{T = t} &= 0, & \text{para cada $t < 0$},\end{align*}
mientras que para $t = 0$, se tiene que $\Prob{T = 0} = \Prob{V = 0} = \frac{1}{8}$. Para $t > 0$, vimos previamente que $g^{-1}[\{t\}] = \{ \sqrt{t}, -\sqrt{t} \}$. Así, tendremos que
\begin{align*} \Prob{T = t} = \sum_{v \in g^{-1}[\{ t \}]} \Prob{V = v} = \Prob{V = \sqrt{t}} + \Prob{V = -\sqrt{t}}. \end{align*}
En particular, la v.a. $V$ sólamente toma probabilidades mayores a $0$ en $\{-3, -2, -1, 0, 1, 2, 3 \}$, por lo que $\Prob{T = t} > 0$ para $t \in \{0, 1, 4, 9 \}$, y $\Prob{T = t} = 0$ en otro caso. Así, tenemos que
\begin{align*} \Prob{T = 1} &= \Prob{V = \sqrt{1}} + \Prob{V = -\sqrt{1}} = \frac{1}{2^{|1| + 1}} + \frac{1}{2^{|-1|+1}} = \frac{1}{2^2} + \frac{1}{2^{2}} = \frac{2}{4} = \frac{1}{2}, \\[1em] \Prob{T = 4} &= \Prob{V = \sqrt{4}} + \Prob{V = -\sqrt{4}} = \frac{1}{2^{|2| + 1}} + \frac{1}{2^{|-2|+1}} = \frac{1}{8} + \frac{1}{8} = \frac{1}{4}, \\[1em] \Prob{T = 9} &= \Prob{V = \sqrt{9}} + \Prob{V = -\sqrt{9}} = \frac{1}{2^{|3| + 1}} + \frac{1}{2^{|-3|+1}} = \frac{1}{16} + \frac{1}{16} = \frac{1}{8}. \end{align*}
Alternativamente, podemos obtener una fórmula cerrada para cada $t \in \{1, 4, 9 \}$, que queda así:
\begin{align*} \Prob{T = t} = \Prob{V = \sqrt{t}} + \Prob{V = -\sqrt{t}} &= \frac{1}{2^{{\left|\sqrt{t}\right|} + 1}} + \frac{1}{2^{{\left|-\sqrt{t}\right|} + 1}} \\[1em] &= \frac{1}{2^{\sqrt{t} + 1}} + \frac{1}{2^{\sqrt{t} + 1}} \\[1em] &= \frac{2}{2^{\sqrt{t} + 1}} \\[1em] &= \frac{1}{2^{\sqrt{t}}}.\end{align*}
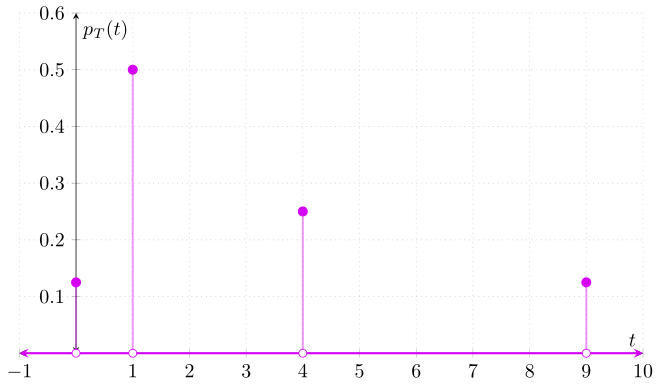
Y así obtenemos una expresión para la función de masa de probabilidad de $T$:
\begin{align*} p_{T}(t) = \begin{cases} \dfrac{1}{2^{\sqrt{t}}} & \text{si $t \in \{1,4,9\}$}, \\[1em] \dfrac{1}{8} & \text{si $t = 0$}, \\[1em] 0 & \text{en otro caso}. \end{cases} \end{align*}
Tarea moral
Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.
- Verifica que la función de masa de probabilidad de la v.a. $Z$ del primer ejemplo satisface las propiedades de una función de masa de probabilidad.
- Haz lo mismo para la función de masa de probabilidad de la v.a. $V$ del segundo ejemplo.
- Retomando los dos ejemplos vistos en esta entrada y las v.a.’s $Z$ y $V$ de cada ejemplo, y tomando la transformación $f\colon\RR\to\RR$ dada por $f(x) = x^{3} − x^{2} − 4x + 4$:
- Encuentra la función de masa de probabilidad de $f(Z)$.
- Encuentra la función de masa de probabilidad de $f(V)$.
Más adelante…
El método expuesto en esta entrada funciona para cualquier variable aleatoria discreta. No hay fórmulas «cerradas» para la f.m.p. (función de masa de probabilidad) de la transformación de una v.a. discreta. Sin embargo, las fórmulas \eqref{transf:1} y \eqref{transf:2} son suficientes para encontrar las probabilidades de eventos que involucran a la transformación de la v.a. discreta conocida. No obstante, estas fórmulas sólamente funcionan para v.a.’s discretas. Por ello, en la siguiente entrada centraremos nuestra atención en el caso de las v.a.’s continuas.
Entradas relacionadas
- Ir a Probabilidad I
- Entrada anterior del curso: Variables Aleatorias Mixtas
- Siguiente entrada del curso: Transformaciones de V.A.’s Continuas