(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
La estrella de esta entrada es el primero de los cuatro Teoremas de Isomorfía que veremos. Como el nombre indica, estos teoremas relacionan dos conjuntos a través de una isomorfía, pero no sólo eso, además en los conjuntos que se relacionan aparece un cociente de grupos. El primer teorema de isomorfía nos permite entender cómo están relacionados el dominio, el núcleo y la imagen de un homomorfismo de grupos, de forma similar al teorema de la dimensión en Álgebra lineal, que establece la relación entre el dominio, el núcleo y la imagen de una transformación lineal.
El Primer Teorema de Isomorfía se usa en la prueba del resto de los teoremas de isomorfía, así que al final de esta unidad te quedará muy claro cómo se usa y para qué sirve. Normalmente se usa definiendo un homomorfismo clave para que al aplicarlo en el grupo obtengamos los cocientes necesarios.
Si quieres reforzar algunos temas que usaremos mucho a lo largo de estas entradas, puedes revisar los conceptos de Subgrupo Normal, Cociente de grupos, Isomorfísmos y Núcleo e Imagen de un Homomorfismo. Será de mucha ayuda que los tengas presentes.
Por último, junto con los Teoremas de Isomorfía usaremos una ayuda visual llamada Diagrama de Retícula, es importante para describir las relaciones entre los distintos grupos, subgrupos y subgrupos normales que estaremos manejando.
El Teorema que vamos a tratar
Teorema. (Primer Teorema de Isomorfía)
Sean $G,\bar{G}$ grupos, $\varphi: G\to \bar{G}$ un homomorfismo. Entonces
\begin{align*}
G/\text{Núc }\varphi \cong \text{Im }\varphi.
\end{align*}
Demostración.
Sea $G,\bar{G}$ grupos, $\varphi: G\to \bar{G}$ un homomorfismo, $N =\text{Núc }\varphi$.
En la entrada anterior probamos que $N \unlhd G$, de modo que $G/\text{Núc }\varphi$ tiene estructura de grupo.
Para probar que $G/\text{Núc }\varphi$ y $\text{Im }\varphi$ son isomorfos, tenemos que dar un isomorfismo entre ellos. Primero construiremos una función que vaya de $G/N$ a $\text{Im }\varphi$. Sea
\begin{align*}
\psi : G/N &\to \text{Im }\varphi \\
a N &\mapsto \varphi(a) \quad \forall a \in G.
\end{align*}
Definiremos nuestra función $\psi$ como aquella que manda una clase $aN$ de $G/N$ a $\varphi(a)$, pero no queda claro si al tomar otro representante de la clase, digamos $b$, sucederá que $\varphi(a) = \varphi(b)$. Esto tenemos que probarlo.
Tomemos $a,b\in G$ tales que $aN = bN$. Entonces,
\begin{align*}
aN = bN &\Leftrightarrow a^{-1}b\in N \\
&\Leftrightarrow \varphi(a^{-1}b) = e_{\bar{G}}\\
& \Leftrightarrow \varphi(a^{-1}) \varphi(b) = e_{\bar{G}}\\
& \Leftrightarrow (\varphi(a))^{-1}\varphi(b) = e_{\bar{G}} &\text{Propiedades de homomorfismos}\\
& \Leftrightarrow \varphi(b) = \varphi(a).
\end{align*}
En realidad todas las equivalencias anteriores son producto de las propuedades de homomorfismos que ya vimos. Las implicaciones de ida ($\Rightarrow$) nos dicen que $\psi$ está bien definida, como queríamos probar. Pero las implicaciones de regreso ($\Leftarrow$) nos dicen algo más: nuestra $\psi$ es inyectiva.
Por lo tanto $\psi$ está bien definida y es inyectiva.
Ahora nos falta ver que en efecto $\psi$ es un homomorfismo y es suprayectiva.
Para ver que es un homomorfismo consideremos $a,b\in G$, entonces:
\begin{align*}
\psi(aNbN) = \psi(abN) = \varphi(ab) = \varphi(a)\varphi(b) = \psi(aN)\psi(bN).
\end{align*}
Lo anterior sale de la definición de $\psi$ y de que $\varphi$ es un homomorfismo. Así, $\psi$ es un homomorfismo.
Finalmente, si $c \in \text{Im }\varphi$, $c = \varphi(a)$ con $a\in G$. Entonces, por definición:
\begin{align*}
c = \varphi(a) = \psi(aN) \in \text{Im }\psi.
\end{align*}
Así, $\psi$ es suprayectiva.
Por lo tanto tenemos que $\psi$ es un homomorfismo inyectivo y suprayectivo, es decir, $\psi$ es un isomorfismo. En consecuencia, $G/N \cong \text{Im }\varphi$.
$\blacksquare$
Diagrama de retícula
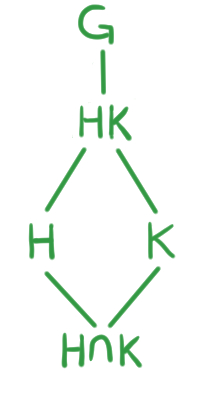
A partir de las siguientes entradas comenzaremos a usar algo llamado diagrama de retícula. Este diagrama es una manera de representar la relación de ser subgrupo. Se escriben todos o algunos subgrupos de un grupo $G$, y se unen dos subgrupos $H$ y $K$ con una arista si $H$ es subgrupo de $K$, de modo que $H$ quede más abajo que $K$. De esta manera, si se consideran todos los sugrupos de $G$ el grupo $G$ aparece hasta arriba y el subrgupo $\{e\}$ hasta abajo del diagrama.
Veamos un ejemplo: Sea $G$ un grupo y $H,K$ subgrupos de $G$. Si consideramos $HK$, sabemos que es subgrupo de $G$, pero además, sabemos que $H\leq HK$ y $K\leq HK$. Por último, consideremos $H\cap K$, que es a su vez un subgrupo de $H$ y $K$.
Todo esto se puede resumir en el siguiente diagrama de retícula:
¿Por qué no unimos $H$ con $G$? Pues porque este diagrama es transitivo, es decir como $H \leq HK \leq G$, está implícito que $H \leq G$. Tampoco unimos un grupo consigo mismo.
Además, si un subgrupo es un subgrupo normal, anotaremos el símbolo $\unlhd$.
Observemos que si $H\unlhd G$, entonces todo elemento en $H$, al ser conjugado con elementos de $G$, sigue siendo un elemento de $H$. En particular, si conjugamos a un elemento de $H$ con un elemento de $HK$ seguimos obteniendo un elemento de $H$. Esto nos dice que $H$ también es normal en $HK$. En el diagrama, la propiedad de ser normal se escribe de la siguiente manera:
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Sea $G$ un grupo cíclico con $G = \left<a\right>$. Considera el homomorfosmo $\varphi: \z \to G$ dado por $\varphi(m) = a^m$ para toda $m\in \z$.
- Si $a$ es de orden finito con $o(a) = n$ ¿qué concluyes al aplicar el 1er Teorema de Isomorfía? ¿Qué relación existe entre dos grupos cíclicos finitos de orden $n$?
- Si $a$ es de orden infinito ¿qué concluyes al aplicar en 1er Teorema de Isomorfía? ¿Qué relación existe entre dos grupos cíclicos infinitos?
- Puedes revisar los siguientes videos que hablan de homomorfismos:
Más adelante…
Uno de los principales usos del Primer Teorema de Isomorfía es definiendo una $\varphi$ ideal para que el núcleo y la imágen de $\varphi$ sean justo lo que queremos probar. Esto lo veremos en la siguiente entrada, donde lo usamos para probar el Segundo Teorema de Isomorfía.
El diagrama de retícula se volverá fundamental sobretodo cuando veamos el Cuarto Teorema de Isomorfía, porque veremos cómo relacionar muchos subgrupos con grupos cocientes correspondientes.
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Núcleo e Imagen de un homomorfismo.
- Siguiente entrada del curso: Segundo Teorema de Isomorfía.
- Resto de cursos: Cursos.