Introducción
Anteriormente se revisó el concepto de continuidad, característica de la cual emanaban diversas propiedades útiles tal como el teorema del valor intermedio. En esta ocasión, daremos inicio con la séptima unidad que estará enfocada al aspecto teórico de uno de los conceptos más conocidos dentro de las matemáticas: la derivada.
El objetivo de esta entrada es entender este nuevo concepto para que posteriormente podamos analizar las propiedades y aplicaciones que posee.
Interpretación geométrica
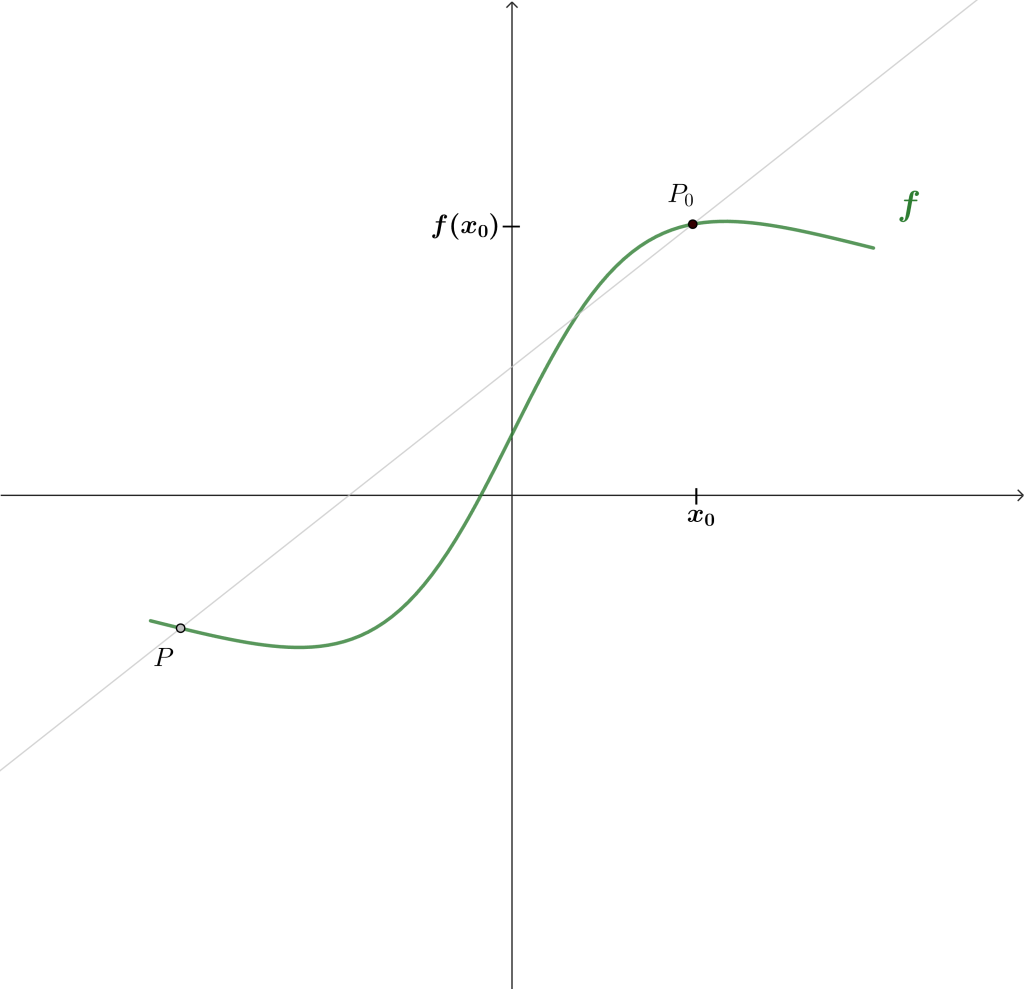
Comenzaremos estudiando la interpretación geométrica para construir la definición formal. Pensemos en la siguiente función y notemos los dos puntos marcados.
Considerando que el punto gris está dado por $P = (x, f(x))$ y el punto negro por $P_0 = (x_0, f(x_0))$, podríamos obtener fácilmente la pendiente de la recta que pasa por ambos puntos.
$$m = \frac{f(x)-f(x_0)}{x-x_0}. \tag{1}$$
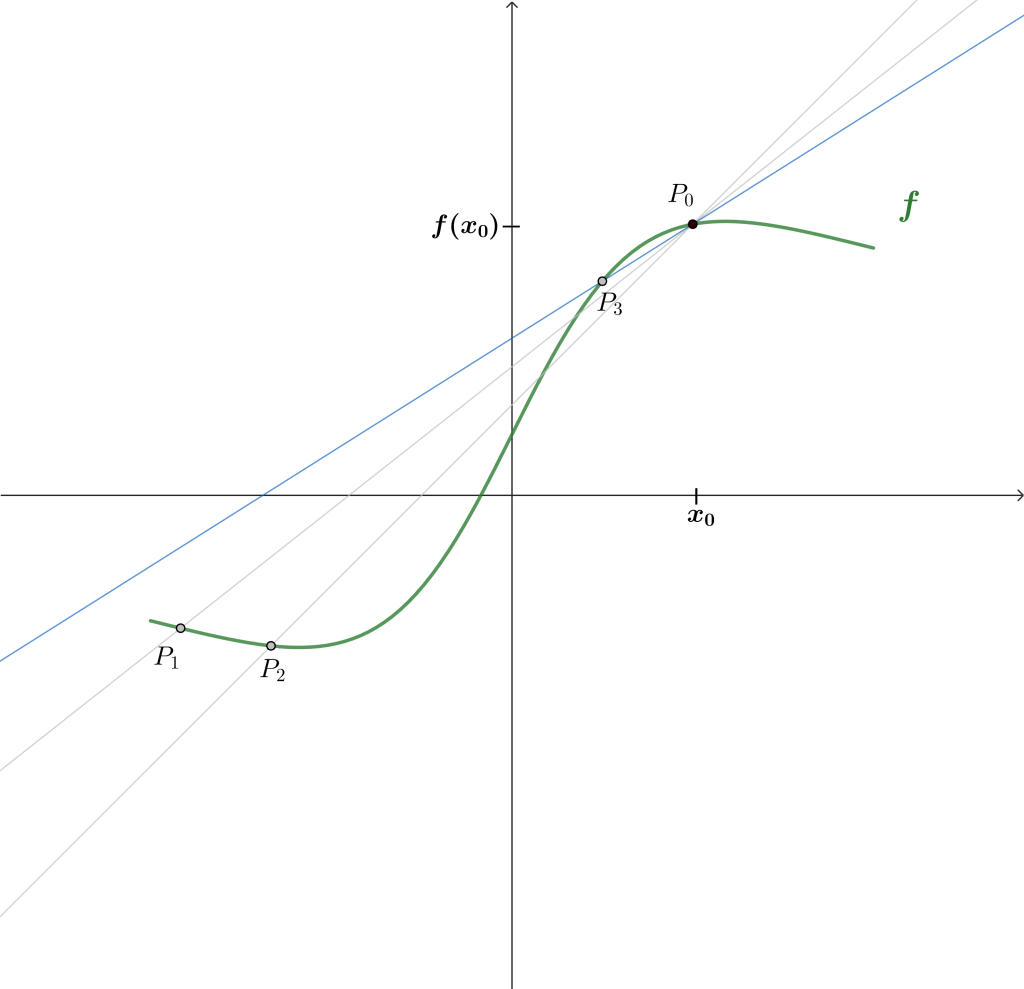
¿Qué sucede si dejamos a $P_0$ como un punto fijo y «movemos» el punto $P$ de tal forma que estos puntos comienzan a estar cada vez más cerca? (En la gráfica, el «movimiento» de $P$ se plasma mediante los puntos $P_1$, $P_2$, y $P_3$)
Si tales puntos están cada vez están más cerca, el concepto de límite entra en juego, pues estaríamos buscando $P \to P_0$. Así, podríamos calcular la pendiente de la recta tangente en el punto $P_0$. De esta forma, el límite deseado es el siguiente:
$$\lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0}.$$
La derivada
Definición. La función $f$ es derivable en $x_0$ si el siguiente límite existe
$$\lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0}.$$
En este caso, denotaremos al límite anterior como $f'(x_0)$ y le llamaremos derivada de $f$ en $x_0.$
También es común encontrar la siguiente definición equivalente de la derivada.
Definición. La función $f$ es derivable en $x_0$ si el siguiente límite existe
$$\lim_{h \to 0} \frac{f(x_0+h)-f(x_0)}{h}.$$
Ahora que conocemos la definición de derivada, es momento de ponerla en práctica y revisar algunas funciones que sean derivables.
Ejemplo 1. Prueba que la función $f(x) = c$, con $c \in \RR$, es derivable para cualquier $x_0 \in \mathbb{R}.$
Demostración
Sea $x_0 \in \RR$. Veremos que $$\lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0}$$ sí existe.
Notemos que si $x \neq x_0$, entonces
\begin{align*}
\frac{f(x)-f(x_0)}{x-x_0} & = \frac{c-c}{x-x_0} \\
& = \frac{0}{x-x_0} \\
& = 0.
\end{align*}
Por lo anterior, se sigue que
$$ \lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0} = 0.$$
Por lo tanto, $f$ es derivable en $\mathbb{R}$ y $f'(x) = 0$.
$\square$
Ejemplo 2. Prueba que la función $f(x) = ax+b$ es derivable para cualquier $x_0 \in \mathbb{R}.$
Demostración
Sea $x_0 \in \RR$. Bastará probar que el límite $$\lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0}$$ sí existe.
Para ello, primero veamos que si $x \neq x_0$, entonces
\begin{align*}
\frac{f(x)-f(x_0)}{x-x_0} & = \frac{ax+b – (ax_0+b)}{x-x_0} \\
& = \frac{ax-ax_0}{x-x_0} \\
& = \frac{a(x-x_0)}{x-x_0} \\
& = a.
\end{align*}
Por lo anterior, se sigue que
$$ \lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0} = a.$$
Por lo tanto, $f$ es derivable en $\mathbb{R}$ y $f'(x) = a$.
$\square$
Continuemos con un segundo ejemplo sencillo para acostumbrarnos a este nuevo concepto.
Ejemplo 3. Prueba que la función $f(x) = x^2$ es derivable para cualquier $x \in \mathbb{R}.$
Demostración.
Sea $x_0 \in \RR.$
Procederemos a calcular el límite directamente.
\begin{align*}
\lim_{x \to x_0} \frac{ f(x)-f(x_0) }{ x-x_0 } & = \lim_{x \to x_0} \frac{x^2 – x_0^2}{x-x_0} \\
& = \lim_{x \to x_0} \frac{ (x-x_0)(x+x_0) }{ x-x_0 } \\
& = \lim_{x \to x_0} x+x_0 \\
& = 2x_0.
\end{align*}
Por lo tanto, $f$ es derivable para cualquier $x \in \RR$ y $f'(x) = 2x$.
$\square$
Ejemplo 4. Prueba que la función $f(x) = \sqrt{x}$ es derivable para cualquier $x_0 > 0.$
Demostración
Sea $x_0 > 0$. Para esta demostración, usaremos la segunda definición de límite.
Notemos que si $h \neq 0$, entonces
\begin{align*}
\frac{f(x_0+h)-f(x_0)}{h} & = \frac{\sqrt{x_0+h}-\sqrt{x_0}}{h} \\
& = \frac{\sqrt{x_0+h}-\sqrt{x_0}}{h} \cdot \frac{\sqrt{x_0+h}+\sqrt{x_0}}{\sqrt{x_0+h}+\sqrt{x_0}} \\
& = \frac{x_0+h-x_0}{h \left( \sqrt{x_0+h}+\sqrt{x_0} \right)} \\
& = \frac{h}{h \left( \sqrt{x_0+h}+\sqrt{x_0} \right)} \\
& = \frac{1}{ \sqrt{x_0+h}+\sqrt{x_0} }.
\end{align*}
Por lo anterior, se sigue que
$$ \lim_{h \to 0} \frac{f(x_0+h)-f(x_0)}{x-x_0} = \frac{1}{2 \sqrt{x_0}}.$$
Por lo tanto, $f$ es derivable para cualquier $x > 0$ y $f'(x) = \frac{1}{2 \sqrt{x}}$.
$\square$
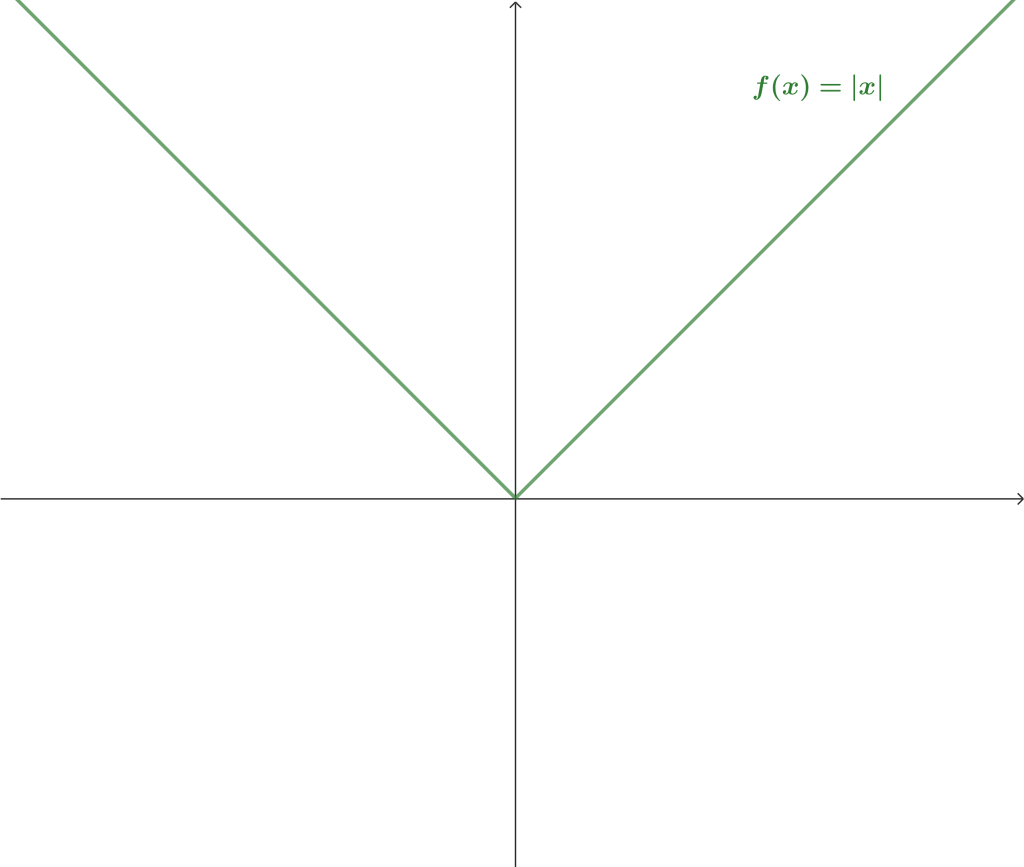
Es momento de revisar una función que no sea derivable. Para este propósito, emplearemos la función valor absoluto, la cual hemos revisado anteriormente y será conveniente que tengas presente su gráfica, pues este tipo de funciones que generan un «pico» en su gráfica, no son derivables en tal punto.
Ejemplo 5. Sea $f: \RR \to \RR$, $f(x) = |x|$. Prueba que $f$ no es derivable en $x_0 = 0.$
Demostración.
Notemos que $$\lim_{x \to x_0} \frac{|x|-0}{x-0} = \lim_{x \to x_0} \frac{|x|}{x}.$$
Consideremos las sucesiones $\{a_n\}$, $\{b_n\}$ donde $a_n = \frac{1}{n}$ y $b_n = -\frac{1}{n}$. Tenemos que $a_n$, $b_n \in \RR$ para todo $n \in \mathbb{N}$. Además, $a_n$, $b_n \neq 0$ para todo $n \in \mathbb{N}$ y $$\lim_{n \to \infty} a_n = 0 = \lim_{n \to \infty} b_n.$$
Pero se tiene que
\begin{align*}
\lim_{n \to \infty} \frac{|a_n|}{a_n} & = \lim_{n \to \infty} \frac{|\frac{1}{n}|}{\frac{1}{n}} \\
& = \lim_{n \to \infty} \frac{\frac{1}{n}}{\frac{1}{n}} \\
& = 1.
\end{align*}
Además
\begin{align*}
\lim_{n \to \infty} \frac{|b_n|}{b_n} & = \lim_{n \to \infty} \frac{|-\frac{1}{n}|}{-\frac{1}{n}} \\
& = \lim_{n \to \infty} \frac{\frac{1}{n}}{-\frac{1}{n}} \\
& = -1.
\end{align*}
De lo que se concluye que el límite $$\lim_{x \to x_0} \frac{|x|-0}{x-0}$$ no existe.
Por tanto, $f$ no es derivable en $x_0= 0$.
$\square$
Intuitivamente, podemos notar que si tratáramos de encontrar una «recta tangente» en $x_0 = 0$ moviéndonos por la derecha, será distinta a la «recta tangente» a generada por la izquierda. Esto hace que el límite no exista, sin embargo, podemos ser menos restrictivos en la definición.
Derivadas laterales
De forma complementaria, podemos definir la derivada en términos de la forma en que $x \to x_0$, es decir, a través de los límites laterales. Así, tenemos las siguientes definiciones.
Definición.
- La función $f$ es derivable por la derecha en $x_0$ si el siguiente límite existe
$$\lim_{x \to x_0^+} \frac{f(x)-f(x_0)}{x-x_0}.$$
En este caso, denotaremos al límite anterior como $f'(x_0^+)$ y le llamaremos derivada por la derecha de $f$ en $x_0$. - La función $f$ es derivable por la izquierda en $x_0$ si el siguiente límite existe
$$\lim_{x \to x_0^-} \frac{f(x)-f(x_0)}{x-x_0}.$$
En este caso, denotaremos al límite anterior como $f'(x_0^-)$ y le llamaremos derivada por la derecha de $f$ en $x_0$.
Más adelante…
En la siguiente entrada revisaremos la relación existente entre la derivabilidad y la continuidad. Además, revisaremos algunas propiedades que nos permitirán obtener la derivada de una función con mayor facilidad.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Da un ejemplo de función que no sea derivable en un punto $x_0$.
- Prueba que la función $f: \RR \to \RR$ definida por $f(x) = ax^2+bx+c$ es derivable en todo $\RR$.
- Prueba que la función $f: \RR \to \RR$ definida por $f(x) = x^3-8$ es derivable en todo $\RR$.
- Demuestra que $f(x) = |x|$ es derivable para todo $x \neq 0$.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral I
- Entrada anterior del curso: Continuidad de la función inversa
- Siguiente entrada del curso: Derivabilidad y continuidad
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»