(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Repasemos un poco el último ejemplo de la entrada anterior. En $S_5$ teníamos la composición $(1 \; 2 \; 3 \; 4)(2 \; 4 \; 5)$ y fijándonos en qué ocurre con cada elemento, concluimos que esta composición es igual a $(1 \; 2)(3 \; 4 \; 5)$. Entonces obtuvimos dos composiciones distintas para escribir a esa permutación. En el dibujo, es más claro que en la primera los dos ciclos se están entrelazando entonces es más difícil entender qué es lo que hace la permutación. Pero cuando vemos la representación de $(1 \; 2)(3 \; 4 \; 5)$ es más fácil entender qué es lo que está haciendo nuestra permutación. Así, es más conveniente trabajar con la segunda notación.

A simple vista podemos observar que $(1 \; 2 \; 3 \; 4)$ y $(2 \; 4 \; 5)$ comparten el 2, pero $(1 \; 2)$ y $(3 \; 4 \; 5)$ no comparten ningún elemento. En este caso, se dice que $(1 \; 2)$ y $(3 \; 4 \; 5)$ son ciclos disjuntos. Más aún, ¿será que cualquier permutación se puede descomponer en ciclos disjuntos? la respuesta es que sí, esto lo demostraremos también en esta entrada.

Definición de permutaciones disjuntas

Antes de definir lo que significa que dos permutaciones sean disjuntas, nos gustaría recordar la última observación de la entrada anterior.
Observación. Si $n \geq 3$, entonces $S_n$ no es abeliano.
Esto nos sirve para establecer que, en general, trabajaremos con grupos no abelianos.

Ahora sí definamos lo que son permutaciones disjuntas.
Definición. Sean $\alpha, \beta \in S_n$. Decimos que $\alpha$ y $\beta$ son disjuntas o ajenas si sop$\,\alpha \,\cap $ sop$\,\beta = \emptyset$, es decir, dado $i\in \{1,2,\dots, n\}$ se tiene que

\begin{align*}
\alpha(i) \neq i &\Rightarrow \beta(i) = i .\\
\end{align*}

En consecuencia también ocurre que si $\beta(i) \neq i$, entonces $\alpha(i) = i.$

Observación. Si $\alpha$ y $\beta$ son disjuntas, pueden fijar a un mismo elemento pero no mover a un mismo elemento.

En particular, si tenemos dos ciclos de longitud mayor a uno, podemos obtener la siguiente equivalencia.
Observación. Sean $\alpha = (i_1 \dots i_r)$ y $\beta = (j_1 \dots j_t)$ con $r,t > 1$. Entonces $\alpha$ y $\beta$ son disjuntas si y sólo si $\{i_1, \dots, i_r\} \cap \{j_1, \dots, j_t\} = \emptyset$.

Ejemplos.

• $(1 \; 2 \; 3 \; 4)$ y $(2 \; 4 \; 5)$ no son disjuntas.
• $(1 \; 2)$ y $(3 \; 4 \; 5)$ sí son disjuntas.

Las permutaciones disjuntas conmutan

Lema. Sean $\alpha, \beta \in S_n$. Si $\alpha$ y $\beta$ son disjuntas, entonces conmutan.

P.D. $\alpha \beta = \beta \alpha$.
Sea $i \in \{1, \dots, n\}$.

Caso 1. Cuando $\alpha(i) = i$, $\beta(i) = i$. Ambas fijan al mismo elemento, esto es posible en permutaciones disjuntas. Entonces, al componer, no importará que permutación se aplique primero.
\begin{align*}
\alpha\beta(i) = \alpha(i) = i = \beta(i) = \beta\alpha(i).
\end{align*}

Caso 2. Cuando $\alpha(i) = i$, $\beta(i) \neq i$.
Si componemos, obtenemos $\beta\alpha(i) = \beta(i)$.
Como $\beta$ es inyectiva y $\beta(i) \neq i$, entonces $\beta(\beta(i)) \neq \beta(i)$. Así $\beta$ mueve a $\beta(i)$ y como $\alpha$ y $\beta$ son disjuntas $\alpha$ fija a $\beta(i)$. Entonces
\begin{align*}
\alpha\beta(i) = \alpha(\beta(i)) = \beta(i).
\end{align*}
Por lo tanto $\beta\alpha(i) = \alpha\beta(i)$.

Caso 3. Cuando $\alpha(i) \neq i$, $\beta(i) = i$.
Este es análogo al caso 2.

El caso $\alpha(i) \neq i$, $\beta(i) \neq i$ no se da pues $\alpha$ y $\beta$ son disjuntas.
Por lo tanto $\alpha\beta = \beta\alpha$.

$\blacksquare$

Toda permutación se puede descomponer en ciclos disjuntos

Comencemos como un ejemplo. Consideremos a la permutación $\alpha \in S_9$

\begin{align*}
\alpha = \begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\
3 & 4 & 1 & 7 & 8 & 6 & 2 & 9 & 5
\end{pmatrix}.
\end{align*}

• El 1 va al 3 y el 3 regresa al 1, entonces tenemos una transposición $(1 \; 3)$.
• Luego, observemos que el 2 va al 4, el 4 al 7 y el 7 al 4. Así tenemos un $3-$ciclo, $(2 \; 4 \; 7)$.
• De los números que no han aparecido hasta ahora, podemos tomar el 5, este va al 8, el 8 al 9 y el 9 regresa al 5. Entonces tenemos otro $3-$ciclo $(5 \; 8 \; 9)$.
• Por último, el 6 queda fijo.

Esto se puede dibujar de la siguiente manera:

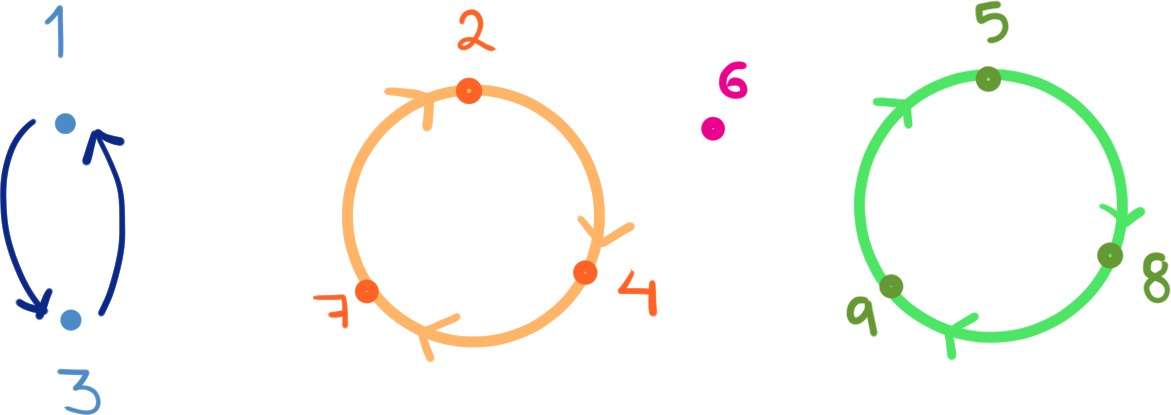
Pero también se puede escribir algebraicamente como:

\begin{align*}
\alpha = (1 \; 3)\,(2 \; 4 \; 7)\,(5 \; 8 \; 9)\,(6).
\end{align*}

Ahora veremos que cualquier permutación se puede descomponer en un producto de ciclos disjuntos.

Analicemos primero cómo se construyen los ciclos a partir de un número en su soporte.

Observación 1. Sean $t\in\mathbb{N}^+$, $\sigma\in S_n$ un $t$-ciclo e $i\in \text{sop } \sigma$. Entonces $$\sigma=(i\; \sigma(i) \;\sigma^2(i)\dots \sigma^{t-1}(i))$$ con $t=\text{mín}\{j\in \mathbb{N}^+| \sigma^{j}(i)=i\}.$

Demostración.

Sean $t\in\mathbb{N}^+$, $\sigma\in S_n$ un $t$-ciclo e $i\in \text{sop } \sigma$. Sabemos que $\sigma$ es de la forma $$\sigma=(i_0\; i_1 \cdots i_{t-1})$$ con $i_0, i_1, \dots , i_{t-1}$ distintos. Como $i\in \text{sop } \sigma=\{i_0, i_1, \dots , i_{t-1}\}$ podemos suponer sin pérdida de generalidad que $i=i_0$ por lo que $\sigma=(i\; i_1 \cdots i_{t-1})$. Entonces

\begin{align*}\sigma(i)&=i_1, \\\sigma^2(i)&=\sigma(\sigma(i))=\sigma(i_1)=i_2\end{align*} y en general $\sigma^j(i)=i_{j}$ para toda $1\leq j<t$ por lo que $$\sigma=(i\; \sigma(i) \;\sigma^2(i)\cdots \sigma^{t-1}(i))$$ con $i,\sigma(i) ,\sigma^2(i),\dots , \sigma^{t-1}(i)$ distintos. En particular $\sigma(i) ,\sigma^2(i),\dots , \sigma^{t-1}(i)$ son distintos de $i$ y además $\sigma^t(i)=\sigma(\sigma^{t-1}(i))=\sigma(i_{t-1})=i$ por lo que $t=\text{mín}\{j\in \mathbb{N}^+| \sigma^{j}(i)=i\}.$

Veamos ahora qué ocurre si la permutación no es necesariamente un ciclo. Probemos que cada número movido por la permutación da lugar a un ciclo.

Lema 1. Sea $\alpha\in S_n$, $i\in\{1,\dots , n\}$. Para cada $i\in\text{sop }\alpha$ existe $j\in\mathbb{N}^+$ tal que $\alpha ^{j}(i)=i$, más aún, si $t_i=\text{mín}\{j\in\mathbb{N}^+\mid \alpha ^{j}(i)=i\}$ se tiene que $i , \alpha(i), \alpha^2(i), \dots ,\alpha^{t_i-1}(i)$ son distintos.

Demostración.
Sea $\alpha \in S_n$, $i\in\text{sop }\alpha$ . Consideremos
\begin{align*}
i , \alpha(i), \alpha^2(i), \dots
\end{align*}

Sabemos que esta lista tiene elementos repetidos ya que consiste de números en el conjunto finito $\{1,2,\dots,n\}$. Existen entonces $r,s\in\mathbb{N}$ distintos tales que $\alpha^r(i) = \alpha^s(i)$, sin pérdida de generalidad $s < r,$ por lo cual $ \alpha^{r-s}(i) = i$ con $ r-s\in\mathbb{N}^+$ como se quería demostrar.

Así, el conjunto $\{j\in\mathbb{N}^+\mid \alpha ^{j}(i)=i\}$ es no vacío, y por el principio del buen orden tiene un elemento mínimo, digamos $t_i$. Veamos ahora que $i , \alpha(i), \alpha^2(i), \dots ,\alpha^{t_i-1}(i)$ son distintos. Supongamos que $\alpha^q(i) = \alpha^l(i)$ para algunos $0\leq q\leq l < t_i$, entonces $\alpha^{l-q}(i) = i$ con $ 0\leq l-q<t_i$ y por la elección de $t_i$ esto implica que $l-q=0$, es decir que $q=l$. Por lo tanto $i , \alpha(i), \alpha^2(i), \dots ,\alpha^{t_i-1}(i)$ son distintos.

$\blacksquare$

Gracias al lema anterior podemos considerar el ciclo $(i\; \alpha (i)\cdots \alpha ^{t_i-1}(i))$:

Definición. Sea $\alpha\in S_n$, $i\in\text{sop }\alpha$ . El ciclo definido por $\alpha$ y por $i$ es

$$\sigma_{\alpha,i}=(i\; \alpha (i)\cdots \alpha ^{t_i-1}(i))\text{ con }t_i=\text{mín}\{j\in\mathbb{N}^+\mid \alpha ^{j}(i)=i\}.$$

Notemos que si $i\in\text{sop }\alpha$, entonces $$\sigma_{\alpha,i}=(i\; \alpha (i)\cdots \alpha ^{t_i-1}(i))= (\alpha (i)\cdots \alpha ^{t_i-1}(i)\;i)= (\alpha^2 (i)\cdots \alpha ^{t_i-1}(i)\;i\;\alpha(i))= \dots, \text{ etc.},$$ por lo que toda $k\in \{i, \alpha (i),\dots , \alpha ^{t_i-1}(i)\}$ define el mismo ciclo que $i$, es decir:

Observación 2. Si $i\in\text{sop }\alpha$, entonces para toda $k\in \{i, \alpha (i),\dots , \alpha ^{t_i-1}(i)\}$ se tiene que $\sigma_{\alpha,k}=\sigma_{\alpha,i}$ y $t_k=t_i.$

En consecuencia tenemos el siguiente resultado:

Lema 2. Sea $\alpha\in S_n$, $i,j\in\text{sop }\alpha$, y consideremos $\sigma_{\alpha,i},\sigma_{\alpha,j}$ como en la definición anterior. Si $\sigma_{\alpha,i}\neq \sigma_{\alpha,j},$ entonces $\sigma_{\alpha,i}$ y $\sigma_{\alpha,j}$ son disjuntos.

Demostración.

Sea $\alpha \in S_n$, $i,j\in\text{sop }\alpha$, $\sigma_{\alpha,i}\neq \sigma_{\alpha,j},$ como en la definición anterior. Probemos el lema por contrapuesta. Supongamos que $\sigma_{\alpha,i}$ y $ \sigma_{\alpha,j},$ no son disjuntos. Existe entonces $k$ movido por ambos ciclos, es decir $k\in\{i, \alpha (i),\cdots \alpha ^{t_i-1}(i)\}\cap\{j, \alpha (j),\cdots ,\alpha ^{t_j-1}(j)\}.$ Por la observación previa tenemos que $\sigma_{\alpha,k}=\sigma_{\alpha,i}$ y $\sigma_{\alpha,k}=\sigma_{\alpha,j}$, de donde concluimos que $\sigma_{\alpha,i}=\sigma_{\alpha,j}$.

$\blacksquare$

Ahora veremos que al considerar todos los ciclos distintos del tipo $\gamma_i$ y componerlos, obtenemos una descomposición de la permutación inicial en ciclos disjuntos:

Teorema. Toda permutación en $S_n$ es un ciclo o un producto de ciclos disjuntos

Demostración.

Sea $\alpha\in S_n$. Consideremos todos los ciclos $\sigma_{\alpha,i}$ con $j\in\text{sop }\alpha$ y eliminemos los ciclos repetidos, llamemos $\gamma_1,\gamma_2,\dots ,\gamma_r$ a los ciclos restantes. Afirmamos que $\alpha=\gamma_1\gamma_2\cdots \gamma_r$ es una descomposición de $\alpha$ en ciclos disjuntos. Por construcción $\gamma_1\gamma_2\cdots \gamma_r$ es un producto de ciclos, y por el lema 2, dado que $\gamma_1,\gamma_2,\dots ,\gamma_r$ son distintos, entonces son también disjuntos. Así, basta convencerse de que $\alpha=\gamma_1\gamma_2\cdots \gamma_r$ para terminar la demostración.

Sea $i\in\{1,2,\dots ,n\}$. Si $i\in\text{sop }\alpha$ tenemos que $\sigma_{\alpha,i}\in\{\sigma_{\alpha,j}\mid j\in\text{sop }\alpha\}=\{\gamma_1,\gamma_2,\dots ,\gamma_r\}$ y entonces $\sigma_{\alpha,i}=\gamma_j$ para alguna $1\leq j\leq r$. Así, $\gamma_j=\sigma_{\alpha,i}=(i\; \alpha (i)\cdots \alpha ^{t_i-1}(i))$ y $$\gamma_1\gamma_2\cdots \gamma_r(i)=\gamma_j(i)=\alpha(i)$$ (donde la primera igualdad se debe a que $\gamma_1,\gamma_2,\dots ,\gamma_r$ son disjuntos). Si $i\notin\text{sop }\alpha$ tenemos que $i\notin\text{sop }\gamma_j$ para toda $j\in\{1,\dots ,r\}$ , por lo que $\gamma_1\gamma_2\cdots \gamma_r(i)=i=\alpha(i)$. Por lo tanto $\alpha=\gamma_1\gamma_2\cdots \gamma_r$ .

$\blacksquare$

Ejemplo.
Sea $\alpha \in S_{10}$ como sigue

\begin{align*}
\alpha = \begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
4 & 1 & 7 & 9 & 6 & 8 & 3 & 5 & 2 & 10
\end{pmatrix}.
\end{align*}

Veamos qué sucede con el $1 \in $ sop $\alpha$. Le aplicamos $\alpha$ varias veces para formar el primer ciclo.

\begin{align*}
1, \alpha(1) = 4, \alpha^2(1) = 9, \alpha^3(1) = 2, \alpha^4(1) = 1.
\end{align*}

Entonces, nombremos $\gamma_1$ a ese $4-$ciclo, $\gamma_1 = (1 \; 4 \; 9 \; 2)$.

Ahora, tomemos un elemento que no esté en $\gamma_1$, digamos $3$. De nuevo, aplicamos $\alpha$ varias veces para descubrir el ciclo al que pertenece.
\begin{align*}
3, \alpha(3) = 7, \alpha^2(3)=3.
\end{align*}

Tenemos así una transposición $\gamma_2=(3\; 7).$

Volvemos a tomar un número que no haya aparecido hasta ahora, digamos $5$. Aplicando $\alpha$ varias veces, podemos descubrir el ciclo,
\begin{align*}
5, \alpha(5) = 6, \alpha^2(5) = 8, \alpha^3(5) = 5,
\end{align*}

obteniendo el ciclo $\gamma_3=(5\;6\;8)$.

Así, nuestra permutación quedaría como
\begin{align*}
\alpha = (1 \; 4 \; 9 \; 2 ) (3 \; 7)( 5 \; 6 \; 8).
\end{align*}

$\blacksquare$

Tarea moral

1. Demuestra la observación: Si $n \geq 3$, entonces $S_n$ no es abeliano.
2. Encuentra dos permutaciones disjuntas $\alpha$ y $\beta$. Encuentra $\beta\alpha$ y $\alpha\beta$ ¿qué observas al comparar $\beta\alpha$? Intenta con otro ejemplo de dos permutaciones disjuntas $\alpha$ y $\beta$ y analiza lo que ocurre.
3. Sean $\alpha$ y $\beta$ dos permutaciones que conmutan ¿podemos concluir entonces $\alpha$ y $\beta$ son disjuntas?
4. Considera el siguiente elemento de $S_{11}$
   \begin{align*}
   \alpha = \begin{pmatrix}
   1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11\\
   5 & 8 & 2 & 6 & 4 & 1 & 3 & 7 & 9 & 11 & 10
   \end{pmatrix}.
   \end{align*}
   Encuentra una factorización en ciclos disjuntos de $\alpha$, y de $\alpha^{-1}$.

Más adelante…

Ya conocemos qué son las permutaciones disjuntas y que cualquier permutación se puede ver como multiplicación de ciclos disjuntos. También, puede que hayas notado que comenzamos a escribir los $1-$ciclos de los elementos que se quedan fijos en las permutaciones. Esto nos encamina al tema principal de la siguiente entrada, la factorización completa, que no es más que la descomposición de una permutación en ciclos disjuntos incluyendo los $1-$ciclos.

Entradas relacionadas

• Ir a Álgebra Moderna I.
• Entrada anterior del curso: Permutaciones y Grupo Simétrico.
• Siguiente entrada del curso: Factorización Completa.
• Resto de cursos: Cursos.