Propiedades de los Conjuntos abiertos y cerrados

Proposición:Si A y B son subconjuntos abiertos de $\mathbb{R}^{n}$, entonces $A\bigcup B$ es un conjunto abierto de $\mathbb{R}^{n}$.
Demostración.
Sea $\overline{x}\in A\cup B$. Se tiene entonces que $\overline{x}\in A$ ó $\overline{x}\in B$. Si $\overline{x}\in A$, entonces, puesto que A es abierto existe $r>0$ tal que $B_{r}(\overline{x})\subset A$, luego $B_{r}(\overline{x})\subset A\cup B$ Si $\overline{x}\in B$, entonces, puesto que B es abierto existe $r>0$ tal que $B_{r}(\overline{x})\subset B$, luego $B_{r}(\overline{x})\subset A\cup B$. En cualquiera de los casos, existe una bola abierta $B_{r}$ contenida en $A\cup B$. $\therefore$ $A\cup B$ es abierto.$~~\blacksquare$

Proposición. Si A y B son subconjuntos abiertos de $\mathbb{R}^{n}$, entonces $A\bigcap B$ es un conjunto abierto de $\mathbb{R}^{n}$.}$
Demostración. Sea $\overline{x}\in A\cup B$. Se tiene entonces que $\overline{x}\in A$ y $\overline{x}\in B$. Puesto que A es abierto $\exists~r_{1}>0$ tal que $B(\overline{x},r_{1})\subset A$. Puesto que b es abierto $\exists~r_{2}>0$ tal que $B(\overline{x},r_{2})\subset B$.\Sea $r=\min{r_{1},r_{2}}$, entonces se tiene que
\begin{align*} B(\overline{x},r) & \subset B(\overline{x},r_{1}) \\ B(\overline{x},r) & \subset B(\overline{x},r_{2}) \end{align*}
Por lo tanto $B(\overline{x},r)\subset A$ y $B(\overline{x},r)\subset B$, o sea $B(\overline{x},r)\subset A\cap B$.$~~\blacksquare$

Proposición. Si A y B son subconjuntos cerrados de $\mathbb{R}^{n}$, entonces $A\bigcup B$ es un conjunto cerrado de $\mathbb{R}^{n}$.}$
Demostración. Para mostrar que $A\bigcup B$ es un conjunto cerrado, tenemos que mostrar que $(A\bigcup B)^{c}$ es un conjunto abierto, al ser A, B conjuntos cerrados entonces $A^{c},~B^{c}$ son conjuntos abiertos y por leyes de D’morgan
$$(A\bigcup B)^{c}=A^{c}\bigcap B^{c}$$
ahora bien por el resultado anterior se tiene que la intersección de conjuntos abiertos es un conjunto abierto, esto prueba que $(A\bigcup B)^{c}$ es un conjunto abierto, por lo tanto $A\bigcup B$ es un conjunto cerrado.$~~\blacksquare$

Proposición. Si A y B son subconjuntos cerrados de $\mathbb{R}^{n}$, entonces $A\bigcap B$ es un conjunto cerrado de $\mathbb{R}^{n}$.}$
Demostración. Para mostrar que $A\bigcap B$ es un conjunto cerrado, tenemos que mostrar que $(A\bigcap B)^{c}$ es un conjunto abierto, al ser A, B conjuntos cerrados entonces $A^{c},~B^{c}$ son conjuntos abiertos y por leyes de D’morgan
$$(A\bigcap B)^{c}=A^{c}\bigcup B^{c}$$
ahora bien por el resultado anterior se tiene que la unión de conjuntos abiertos es un conjunto abierto, esto prueba que $(A\bigcap B)^{c}$ es un conjunto abierto, por lo tanto $A\bigcap B$ es un conjunto cerrado.$~~\blacksquare$

Generalizaciones de la proposiciones anteriores de la familias de conjuntos.

Proposición. La unión arbitraria de conjuntos abiertos en $\mathbb{R}^{n}$ es un conjunto abierto en $\mathbb{R}^{n}$}$
Demostración.
Sea ${A_{\alpha}}$ una colección de subconjuntos de $\mathbb{R}^{n}$ tal que $A_{\alpha}$ es un conjunto abierto en $\mathbb{R}^{n}$. Sea $\displaystyle{A=\bigcup A_{\alpha}}$.
Sea $\overline{x}_{0}\in A$. Entonces existe $\alpha$ tal que $\overline{x}_{0}\in A_{\alpha}$ y como $A_{\alpha}$ es un conjunto abierto, existe $r>0$ tal que
$$B(\overline{x}_{0},r)\subset A{\alpha}\subset \bigcup A_{\alpha}=A$$
Por lo tanto A es abierto.$~~\blacksquare$

Propposición. La intersección finita de conjuntos abiertos en $\mathbb{R}^{n}$ es un conjunto abierto en $\mathbb{R}^{n}$}$
Demostración. Sean $A_{1},A_{2},…,A_{k}$ subconjutos abiertos de $\mathbb{R}^{n}$. Sea $\displaystyle{B=\bigcap_{i=1}^{k}A_{i}=A_{1}\cap A_{2}\cap …\cap A_{k}}$.
Sea $\overline{x}_{0}\in B$. Entonces $\overline{x}_{0}\in A_{i}$ para toda $1\leq i\leq k$. Cada $A_{i}$ es un conjunto abierto. Por lo tanto existe $r_{i}>0$ tal que $B(\overline{x}_{0},r{i})\subset A_{i}$ para toda $1\leq i\leq k$. Sea $r=\min{r_{1},r_{2},…,r_{n}}>0$. Entonces
$$B(\overline{x}_{0},r)\subset B(\overline{x}_{0},r_{i})\subset A_{i}~~\forall~i=1,…,n$$
Por lo tanto
$$B(\overline{x}_{0},r)\subset \bigcap_{i=1}^{k}A_{i}=B$$
y por lo tanto B es un conjunto abierto.$~~\blacksquare$

Proposición. La unión finita de conjuntos cerrados en $\mathbb{R}^{n}$ es un conjunto cerrado en $\mathbb{R}^{n}$}$
Demostración. Sean $A_{1},…,A_{k}\subset \mathbb{R}^{n}$ conjuntos cerrados y sea $\displaystyle{B=\bigcup_{i=1}^{n}A_{i}}$. Entonces
$$B^{c}=\left(\bigcup_{i=1}^{n}A_{i}\right)^{c}=\bigcap_{i=1}^{n}A^{c}_{i}$$
el cual es un conjunto abierto de $\mathbb{R}^{n}$. Por lo tanto B es un conjunto cerrado de $\mathbb{R}^{n}$.$~~\blacksquare$

Proposición. La intersección finita de conjuntos cerrados en $\mathbb{R}^{n}$ es un conjunto cerrado en $\mathbb{R}^{n}$}$
Demostración. Sea ${A_{\alpha}}$ una colección de subconjuntos de $\mathbb{R}^{n}$ tales que cada $A_{\alpha}$ es cerrado en $\mathbb{R}^{n}$. Por lo tanto para cada $\alpha$, $A^{c}{\alpha}$ es un conjunto abierto en $\mathbb{R}^{n}$. Sea $\displaystyle{A=\bigcap{\alpha}A_{\alpha}}$ tal que
$$A^{c}=\left(\bigcap_{\alpha}A_{\alpha}\right)^{c}=\bigcup_{\alpha}A^{c}_{\alpha}$$
es un conjunto abierto en $\mathbb{R}^{n}$. Por lo tanto A es un conjunto cerrado en $\mathbb{R}^{n}$.$~~\blacksquare$

Definición. Un elemento $\bar{x}\in A$ se dice que es un $\textbf{punto interior}$ de $A$, si existe una bola abierta con centro en $\bar{x}$ contenida en $A$ es decir si $\exists$ $r>0$ tal que $B(\bar{a},r)\subset A$. Denotamos por $int(A)$ al conjunto formado por todos estos puntos, es decir $$int(A)=\{\overline{x}\in\mathbb{R}^{n}~|~\overline{x}~es~punto~interior~de~A\}$$
y diremos que este conjunto es el interior de A.

Ejemplo. Determinar el $int(A),~~Fr(A),~~ext(A)$ con
\[
A=\left[0,1\right]\times\left[0,1\right]\cap\left(\mathbb{Q}\times\mathbb{Q}\right)=\left\{ (x,y)\in\mathbb{R}^{2}~\big{|}~(x,y)\in\mathbb{Q}~~y~~0\leq x\leq1~~0\leq y\leq1\right\} .
\]

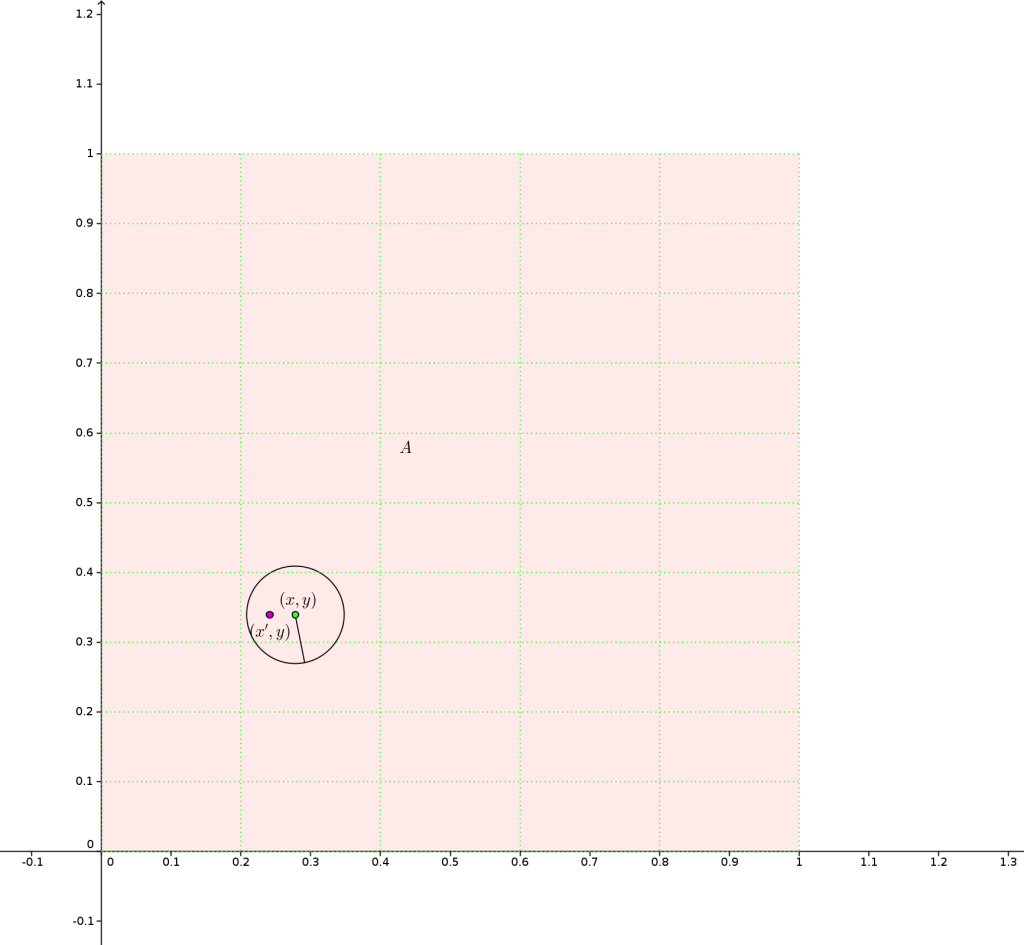
Solución. Primero analicemos la figura, ¿qué pasa si tomamos un $(x,y)$ en $A$ y un $r>0$?, ¿qué podemos observar?. Si recordamos la densidad de los irracionales sabemos que podemos encontrar un $x’$ irracional entre $x$ y $x+r$, entonces si tomamos el punto $(x’,y)$ podemos ver que esta dentro de $B_{r}(x,y)$, pero $(x’,y)$ no es un punto de $A$. Esto pasa para toda $r>0$ y todo $(x,y)$ en $A$. Entonces, podemos afirmar que el $int(A)=\emptyset$.
Ademas, podemos decir que para todo $(x,y)$ en $A$ y todo $r>0$ se tiene que $B_{r}(x,y)\cap A^{c}\neq\emptyset$. Usando el mismo argumento, pero ahora para los racionales, podemos decir que para cualquier $(x,y)$ y $r>0$ se tiene que $B_{r}(x,y)\cap A\neq\emptyset$.
Todo esto dentro del cuadrado $\left[0,1\right]\times\left[0,1\right]$. Entonces, podemos afirmar que $Fr(A)=\left[0,1\right]\times\left[0,1\right]$.

¿Que podemos decir del exterior? De lo anterior podemos deducir que
$ext(A)=\mathbb{R}{{}^2}-\left[0,1\right]\times\left[0,1\right]$.
Entonces, demostremos la siguiente afirmación:

Afirmación: $int(A)=\emptyset$
Demostración. Sean $(x,y)\in A$ y $r>0$. Mostraremos que $B_{r}(x,y)\cap A^{c}\neq\emptyset$, es decir, que para cualquier punto $(x,y)$ de $A$ y cualquier radio $r>0$, la bola $B_{r}(x,y)$ siempre contiene puntos de $A^{c}$, es decir, que $A$ no tiene puntos interiores.
Como $(x,y)\in A$, entonces $x\in\mathbb{Q}$ y por la densidad de los irracionales sabemos que siempre existe un $x’\notin\mathbb{Q}$ tal que $x<x'<x+r$……$\bigstar$
Tomemos el punto $(x’,y)$ y calculemos su distancia con $(x,y)$:
\[
\| (x,y)-(x’,y)\|=\| (x-x’,0)\|=\sqrt{(x-x’)^{2}}=\underset{**}{\underbrace{\left|x-x’\right|<r}}\text{ esta ultima desigualdad se cumple por }\bigstar
\] Veamos por que se cumple $**$. De $\bigstar$ tenemos que $x<x'<x+r$, restando $x$ tenemos $x-x<x’-x<x+r-x$ $\Longrightarrow0<x’-x<r$ como esto es positivo, le podemos sacar el valor absouto y se mantiene la desigualdad $0<|x’-x|<r$ y sabemos que $|a-b|=|b-a|$. Por lo tanto, $|x-x’|<r$.
Entonces, como $\left\Vert (x,y)-(x’,y)\right\Vert <r$, tenemos que $(x’,y)\in B_{r}(x,y)$, pero como $x’\notin\mathbb{Q}$ esto implica que $(x’,y)\notin\mathbb{Q}\times\mathbb{Q}$. Por lo tanto, $B_{r}(x,y)\cap\left(\mathbb{R}^{2}-\mathbb{Q}\times\mathbb{Q}\right)\neq\emptyset$.
Podemos observar que $A\subset\mathbb{Q}\times\mathbb{Q}$ $\Longrightarrow$ $B_{r}(x,y)\cap\left(\mathbb{R}^{2}-A\right)=B_{r}(x,y)\cap A^{c}\neq\emptyset$,
es decir, que para todo $r>0$ se tiene que $B_{r}(x,y)$ siempre interseca a $A^{c}$. Por lo tanto, $int(A)=\emptyset$.$~~\blacksquare$

Afirmación: $Fr(A)=\left[0,1\right]\times\left[0,1\right]$
Demostración. Primero mostraremos que $\left[0,1\right]\times\left[0,1\right]\subset Fr(A)$. Sea $(x,y)\in\left[0,1\right]\times\left[0,1\right]$ y $r>0$. Ya probamos que $B_{r}(x’,y’)\cap A^{c}\neq\emptyset$, falta probar que $B_{r}(x,y)\cap A\neq\emptyset$. (Para que se cumpla la definición de frontera). Tenemos varios casos para $x$ y $y$:
$(1)$ Supongamos que $0\leq x<1$ y $0\leq y<1$. Por la densidad de los números racionales, sabemos que existen $x’,y’\in\mathbb{Q}$ tal que:
\[
x<x'<min\left\{1,x+\frac{r}{\sqrt{2}}\right\},\text{y }y<y'<min\left\{1,y+\frac{r}{\sqrt{2}}\right\}…………………\clubsuit
\]
Entonces, $\underset{\spadesuit}{\underbrace{(x’,y’)\in A}}$ y además $\displaystyle{|x-x’|<\frac{r}{\sqrt{2}}}$ y $\displaystyle{|y-y’|<\frac{r}{\sqrt{2}}}$. Así podemos ver lo siguiente:
\[
||(x,y)-(x’,y’)||=\sqrt{(x-x’)+(y-y’)}<\sqrt{\left(\frac{r}{\sqrt{2}}\right)^{2}+\left(\frac{r}{\sqrt{2}}\right)^{2}}=r,
\]
lo que nos dice que el punto $(x’,y’)\in B_{r}(x,y)$, y por $\spadesuit$ tenemos que $B_{r}(x,y)\cap A\neq\emptyset$.
$(2)$ En este caso juntaremos los casos que faltan. Escogiendo a $x’,y’$ como en $\clubsuit$, tenemos lo siguiente:
(a) Si $x=1$ y $y<1$ nos fijamos en la pareja $(1,y’)$,
(b) Si $x<1$ y $y=1$ nos fijamos en la pareja $(x’,1)$, y
(c) Si $x=1$ y $y=1$nos fijamos en la pareja $(1,1)$.
Podemos observar que estos puntos están en $A$, pues sus entradas pertenecen a los racionales. Por lo tanto, $B_{r}(x,y)\cap A\neq\emptyset$. Por lo tanto, $\left[0,1\right]\times\left[0,1\right]\subset Fr(A)$.

Afirmación: $ext(A)=\mathbb{R}^{2}-\left[0,1\right]\times\left[0,1\right]$
Demostración. Primero mostremos que $\mathbb{R}^{2}-\{\left[0,1\right]\times\left[0,1\right]\}\subset ext(A)$. Sea $(x,y)\in\mathbb{R}^{2}-\{\left[0,1\right]\times\left[0,1\right]\}$
y supongamos que $x<0$ ó $1<x$, (la otra posibilidad es que $y<0$ ó $y>1$, pero se hace de manera análoga).
(1) Si $x<0$, entonces tomamos $r=|x|>0$. Vamos a mostrar que $B_{r}(x,y)\subset\mathbb{R}^{2}-\{\left[0,1\right]\times\left[0,1\right]\}$. Observemos que $\mathbb{R}^{2}\{\left[0,1\right]\times\left[0,1\right]\}\subset A^{c}…………..\spadesuit$.
Sea $(x’,y’)\in B_{r}(x,y)$, sabemos que
\[
|x-x|\leq\left\Vert (x,y)-(x’,y’)\right\Vert <r
\]
pero $|x|=r$, entonces
\[
|x-x’|<|x|=-x\text{ pues }x<0
\]
entonces
\[
x<x-x'<-x\Longrightarrow-x+x<-x+x-x'<-x-x\Longrightarrow0<-x'<-2x
\]
multiplicando por $(-1)$, tenemos que $x'<0$, lo cual implica que
$(x’,y’)\notin\left[0,1\right]\times\left[0,1\right]$. Así tenemos que $(x’,y’)\in\mathbb{R}^{n}-\left[0,1\right]\times\left[0,1\right]$.
Entonces, $B_{r}(x,y)\subset\mathbb{R}^{n}-\left[0,1\right]\times\left[0,1\right]$.
Por lo tanto, por $\spadesuit$, $B_{r}(x,y)\subset A^{c}$, lo cual implica que $(x,y)\in ext(A)$.
(2) Si $x>1$, entonces tomamos $r=x-1>0$.
Vamos a mostrar que $B_{r}(x,y)\subset\mathbb{R}^{2}-\{\left[0,1\right]\times\left[0,1\right]\}$. Observemos que $\mathbb{R}^{2}\{\left[0,1\right]\times\left[0,1\right]\}\subset A^{c}…………..\spadesuit$.
Sea $(x’,y’)\in B_{r}(x,y)$, sabemos que

Vamos a mostrar que $B_{r}(x,y)\subset\mathbb{R}{{}^2}-\left[0,1\right]\times\left[0,1\right]$.
Observemos que $\mathbb{R}{{}^2}\left[0,1\right]\times\left[0,1\right]\subset A^{c}…………..\spadesuit$.\
Sea $(x’,y’)\in B_{r}(x,y)$, sabemos que
\[
|x-x’|\leq\left\Vert (x,y)-(x’,y’)\right\Vert <r=x-1
\]

\[
|x-x’|<x-1\Longrightarrow1-x<x-x'<x-1\Longrightarrow1-2x<x-x-x'<x-x-1
\]

\[
1-2x<-x'<-1\Longrightarrow1<x'<2x-1
\]

entonces tenemos que $x’>1$, lo cual nos dice que $(x’,y’)\notin\left[0,1\right]\times\left[0,1\right]$.
Así tenemos que $(x’,y’)\in\mathbb{R}^{n}-\{\left[0,1\right]\times\left[0,1\right]\}$.
Entonces, $B_{r}(x,y)\subset\mathbb{R}^{n}-\{\left[0,1\right]\times\left[0,1\right]\}$.
Por lo tanto, por $\spadesuit$, $B_{r}(x,y)\subset A^{c}$, lo cual
implica que $(x,y)\in ext(A)$. Por lo tanto, $\mathbb{R}^{2}-\{\left[0,1\right]\times\left[0,1\right]\}\subset ext(A)$.
De la proposición tenemos que $\mathbb{R}^{n}=int(A)\cup ext(A)\cup Fr(A)$,
en nuestro caso obtuvimos que $int(A)=\emptyset$. Entonces,

\[
\mathbb{R}{{}^2}=ext(A)\cup Fr(A)
\]
y de esto obtenemos las siguientes igualdades
\[
\mathbb{R}{{}^2}-ext(A)=Fr(A)………\clubsuit\text{ y }\mathbb{R}{{}^2}-Fr(A)=ext(A)………\clubsuit\clubsuit.
\]
De $\clubsuit$ tenemos $Fr(A)\subset\mathbb{R}{{}^2}-ext(A)$ y de $(2)$ tenemos $\left[0,1\right]\times\left[0,1\right]\subset Fr(A)$, entonces $\left[0,1\right]\times\left[0,1\right]\subset Fr(A)\subset\mathbb{R}{{}^2}-ext(A)………….\maltese$
De $(3)$ tenemos $\mathbb{R}^{2}-\left[0,1\right]\times\left[0,1\right]\subset ext(A)$,
entonces

\[
\left(\mathbb{R}^{2}-\left[0,1\right]\times\left[0,1\right]\right)\cup\left[0,1\right]\times\left[0,1\right]\subset ext(A)\cup\left[0,1\right]\times\left[0,1\right]
\]

entonces
\[
\mathbb{R}^{2}\subset ext(A)\cup\left[0,1\right]\times\left[0,1\right]\Longrightarrow\mathbb{R}^{2}-ext(A)\subset\left(ext(A)\cup\left[0,1\right]\times\left[0,1\right]\right)-ext(A)
\]

así tenemos
\[
\mathbb{R}^{2}-ext(A)\subset\left[0,1\right]\times\left[0,1\right]…………..\maltese\maltese
\]

Entonces, por $\maltese$ y $\maltese\maltese$ tenemos que $Fr(A)=\left[0,1\right]\times\left[0,1\right]$. Y de esta igualdad y de $\clubsuit\clubsuit$ tenemos que $ext(A)=\mathbb{R}^{2}-\left[0,1\right]\times\left[0,1\right]$.$~~\blacksquare$

Proposición:
Si $A\subset\mathbb{R}^{n}$, entonces:
(1) $int(A)\subset A$
(2) $ext(A)\subset A^{c}$
(3) (a) $int(A)\cap ext(A)=\emptyset$, (b) $int(A)\cap Fr(A)=\emptyset$ y (c) $Fr(A)\cap ext(A)=\emptyset$
(4) $\mathbb{R}^{n}=int(A)\cup ext(A)\cup Fr(A)$
(5) $int(A^{c})=ext(A)$ y $Fr(A)=Fr(A^{c})$.

Demostración.
(1) Por demostrar que $int(A)\subset A$. Sea $\hat{x}\in int(A)$ $\Longrightarrow$ por definición que existe $r>0$ tal que $B_{r}(\hat{x})\subset A$. Como $\hat{x}\in B_{r}(\hat{x})$ (por definición de bola), entonces $\hat{x}\in A$. Por lo tanto, $int(A)\subset A$.

(2) Por demostrar que $ext(A)\subset A^{c}$. Sea $\hat{x}\in ext(A)$ $\Longrightarrow$ por definición que existe $r>0$ tal que $B_{r}(\hat{x})\subset A^{c}$. Como $\hat{x}\in B_{r}(\hat{x})$ (por definición de bola), entonces $\hat{x}\in A^{c}$. Por lo tanto, $ext(A)\subset A$.

3_aPor demostrar que $int(A)\cap ext(A)=\emptyset$. Supongamos por contadicción que $int(A)\cap ext(A)\neq\emptyset$, esto implica que existe $\hat{x}\in int(A)\cap ext(A)$ $\Longrightarrow$ $\hat{x}\in int(A)$ y $\hat{x}\in ext(A)$, esto implica por (1) y (2) que $\hat{x}\in A$ y $\hat{x}\in A^{c}$, lo cual es una contradicción. Por lo tanto, $int(A)\cap ext(A)=\emptyset$.

3_b Por demostrar que $int(A)\cap Fr(A)=\emptyset$. Supongamos por contadicción que $int(A)\cap Fr(A)\neq\emptyset$, esto implica que existe $\hat{x}\in int(A)\cap Fr(A)$ $\Longrightarrow$
$\hat{x}\in int(A)$ y $\hat{x}\in Fr(A)$. Así, tenemos lo siguiente: $(a).$ Existe $r>0$ tal que $B_{r}(\hat{x})\subset A$, y $(b).$ Para todo $r’>0$ se tiene que $B_{r’}(\hat{x})\cap A\neq\emptyset$ y $B_{r’}(\hat{x})\cap A^{c}\neq\emptyset$. En particular, por $(a)$, para $r>0$ tenemos que $B_{r}(\hat{x})\cap A^{c}=\emptyset$, lo cual contradice la hipótesis $(b)$. Por lo tanto, $int(A)\cap Fr(A)=\emptyset$.

3_c Por demostrar que $Fr(A)\cap ext(A)=\emptyset$.
Supongamos por contradicción que $Fr(A)\cap ext(A)\neq\emptyset$,
esto implica que existe $\hat{x}\in Fr(A)\cap ext(A)$ $\Longrightarrow$
$\hat{x}\in Fr(A)$ y $\hat{x}\in ext(A)$. Así, tenemos lo siguiente:
$(a).$ Para todo $r>0$ se tiene que $B_{r’}(\hat{x})\cap A\neq\emptyset$
y $B_{r’}(\hat{x})\cap A^{c}\neq\emptyset$, y
$(b).$ Existe $r’>0$ tal que $B_{r’}(\hat{x})\subset A^{c}$.
Así, por $(b)$tenemos que existe $r’>0$ tal que $B_{r’}(\hat{x})\cap A=\emptyset$,
lo cual contradice la hipótesis $(a)$. Por lo tanto, $Fr(A)\cap ext(A)=\emptyset$.

(4) Por demostrar que $\mathbb{R}^{n}=int(A)\cup Fr(A)\cup ext(A)$.
Como $A\subset\mathbb{R}^{n}$, se tiene que $int(A)\cup Fr(A)\cup ext(A)\subset\mathbb{R}^{n}$. Falta ver que $\mathbb{R}^{n}\subset int(A)\cup Fr(A)\cup ext(A)$. Sea $\hat{x}\in\mathbb{R}^{n}$, como $A\subset\mathbb{R}^{n}$entonces tenemos tres casos:

$(a)$ Existe $r>0$ tal que $B_{r}(\hat{x})\subset A$, entonces por
definición tenemos que $\hat{x}\in int(A)$,

$(b)$ existe $r>0$ tal que $B_{r}(\hat{x})\subset A^{c}$, entonces por defición tenemos que $\hat{x}\in ext(A)$, o
$(c)$ para todo $r>0$ se tiene que $B_{r}(\hat{x})\cap A^{c}\neq\emptyset$
y $B_{r}(\hat{x})\cap A\neq\emptyset$, entonces por definición $\hat{x}\in Fr(A)$. Así tenemos que, $\mathbb{R}^{n}\subset int(A)\cup Fr(A)\cup ext(A)$. Por lo tanto, $\mathbb{R}^{n}=int(A)\cup Fr(A)\cup ext(A)$.

$(5)$ (a) Por demostrar que $int(A^{c})=ext(A)$.
$\subset\rfloor$ $int(A^{c})\subset ext(A)$ Sea $\hat{x}\in int(A^{c})$, por definición se tiene que existe $r>0$ tal que $B_{r}(\hat{x})\subset A^{c}$, pero esta es la definición de un punto exterior de $A$. Por lo tanto, $\hat{x}\in ext(A)$. $\supset\rfloor$ $ext(A)\subset int(A^{c})$. Sea $\hat{x}\in ext(A)$, por definición se tiene que existe $r>0$ tal que $B_{r}(\hat{x})\subset A^{c}$, pero esta es la definición de un punto interior de $A^{c}$. Por lo tanto, $\hat{x}\in int(A^{c})$. Por lo tanto, $int(A^{c})=ext(A)$.$~~\blacksquare$

Definición. Sea $A\subset \mathbb{R}^{n}$. Definimos la cerradura de A, que denotamos por $\overline{A}$, como $$\overline{A}=int(A)\cup Fr(A)$$

Proposición. Sea $A\subset \mathbb{R}^{n}$. Las siguientes afirmaciones son ciertas:
(1) $Int(A)$ es un conjunto abierto
(2) $Ext(A)$ es un conjunto abierto
(3) $Fr(A)$ es un conjunto cerrado
(4) $\overline{A}$ es un conjunto cerrado.
Demostración.
(1) Sea $\overline{x}\in Int(A)$, entonces existe $r>0$ tal que $B(\overline{x},r)\subset A$. Sea $\overline{y}\in B(\overline{x},r)$, existe $r’>0$ tal que $B(\overline{y},r’)\subset B(\overline{x},r)\subset A$ por lo que $\overline{y}\in Int(A)$ y por tanto $B(\overline{x},r)\subset Int(A)$.
(2) Como $Ext(A)=Int(A^{c})$ y de acuerdo al inciso anterior este conjunto es abierto.
(3) Tenemos que $$(Fr(A))^{c}=\mathbb{R}^{n}-Fr(A)=int(A)\cup Ext(A)$$
ambos conjuntos son conjuntos abiertos y la unión de conjuntos abiertos es abierta, entonces este conjunto es abierto y por tanto $Fr(A)$ es cerrado.
(4) Se tiene que
$$(\overline{A}^{c})=\mathbb{R}^{n}-(int(A)\cup Fr(A))=ext(A)$$
el cual es conjunto abierto, por lo tanto $\overline{A}$ es un conjunto cerrado.$~~\blacksquare$

Punto de Acumulación

Definición. Sea $A\subset\mathbb{R}^{n}$ y $\overline{x}\in\mathbb{R}^{n}$. Se dice que
(1) $\overline{x}$ es un punto de acumulación de A, si toda bola abierta con centro en $\overline{x}$ contiene un punto de A distinto de $\overline{x}$ es decir $$\forall r>0, \quad \left(B(\overline{x},r)-{\overline{x}}\right)\cap A\neq \emptyset$$
Al conjunto de puntos de acumulación de A se le denomina el $\textbf{conjunto derivado}$ de A y se le denota $A’$.
(2) $\overline{x}\in A$ es un punto aislado de A si $\overline{x}$ no es un punto de acumulación de A, es decir, si existe $r>0$ tal que
$$(B(\overline{x},r)-{\overline{x}})\cap A=\emptyset.$$

Ejemplo. Sea
$$A=\{(x,y)\in\mathbb{R}^{2}~|~x^{2}+y^{2}<1\}$$
Muestre que $\displaystyle{\overline{x}_{0}=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)}$ es un punto de acumulación de A.
Solución. Vamos a considerar el punto $\displaystyle{\overline{x}=\left(\frac{1}{\sqrt{2}(r+1)},\frac{1}{\sqrt{2}(r+1)}\right)}$, para $r>0$.
Tenemos entonces que

(1) $\overline{x}\in A$ pues
\begin{align*} \left(\frac{1}{\sqrt{2}(r+1)}\right)^{2}+\left(\frac{1}{\sqrt{2}(r+1)}\right)^{2} & =\frac{1}{2(r+1)^{2}}+\frac{1}{2(r+1)^{2}} \\ & <\frac{1}{2}+\frac{1}{2}=1 \end{align*}

(2) Tenemos que
\begin{align*} \|\overline{x}-\overline{x}_{0}\| & =\left|\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)-\left(\frac{1}{\sqrt{2}(r+1)},\frac{1}{\sqrt{2}(r+1)}\right)\right| \\ & =\left|\left(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}(r+1)},\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}(r+1)}\right)\right| \\ &=\left|\frac{r}{\sqrt{2}(r+1)},\frac{r}{\sqrt{2}(r+1)}\right| \\ &=\frac{r}{\sqrt{2}(r+1)}\|(1,1)\| \\ &=\frac{r}{\sqrt{2}(r+1)}\sqrt{2} \\ &=\frac{r}{r+1}<r\end{align*}

Tenemos entonces que $\displaystyle{\overline{x}\in B\left(\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right),r\right)}$. Por lo tanto
$$\left[B\left(\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right),r\right)-\left\{\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\right\}\right]\bigcap A\neq \emptyset$$
Por lo tanto $\displaystyle{\overline{x}_{0}=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)}$ es un punto de acumulación de A.$~~\blacksquare$

Más adelante

En la siguiente sección continuaremos estudiando topológicamente los conjuntos importantes obtenidos a partir de la caracterización de puntos de $\mathbb{R}^n$

Tarea Moral

1.- Si $A\subset \mathbb{R^n}$ es un conjunto arbitrario demuestra que $int(A) \subset A´ \subset int(A) \cup Fr(A)$

2.- Sea $A \in \mathbb{R}^n$ prueba que: $A$ no puede ser cerrado y abierto a la vez.

3.- Sea $A \in \mathbb{R}^n$ prueba que: $Fr(A) \neq \phi$

4.-Sean $A$ y $B$ subconjuntos de $\mathbb{R}^n$. Indica y prueba si las siguientes afirmaciónes son ciertas.

a) Si $A \subset B$ entonces $A’ \subset B’$

b) $(A \cup B)’= A’ \cup B ‘$

c) $(A \cap B)’= A’ \cap B ‘$

5.- Sea $A$ un subconjunto de $\mathbb{R}^n$ Prueba que: Si $B \subset A$ y $B$ es abierto, entonces $B \subset int(A)$ (es decir, de los conjuntos abiertos que están contenidos en $A$, $int(A)$ es el más «grande»).