Introducción

Una vez que hemos introducido el concepto de variable aleatoria, nos toca ver qué nuevas definiciones surgen a partir de este. Un primer concepto que surge es la función de distribución. A grandes rasgos, dado un espacio de probabilidad $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$, en la entrada anterior vimos que una función $X:\mathrm{\Omega }\to \mathbb{R}$ debe de satisfacer que para cualquier $x\in \mathbb{R}$, $X^{-1}[(-\mathrm{\infty },x]]$ es un evento de $\mathrm{\Omega }$. Básicamente, esta condición era suficiente para concluir que para cada $B\in \mathcal{B}(\mathbb{R})$ se cumple que $X^{-1}[B]\in \mathcal{F}$. En otras palabras, la imagen inversa de cualquier evento de $\mathbb{R}$ es un evento de $\mathrm{\Omega }$.

De manera similar, lo que haremos será definir la probabilidad de los eventos de la forma $(X\le x)$, con $x\in \mathbb{R}$. No lo veremos aquí (porque no tenemos las herramientas suficientes para hacerlo), pero resulta que asignarle probabilidad a esos eventos captura toda la información relevante sobre una variable aleatoria. Esto nos permitirá prescindir por completo de muchos detalles de la variable aleatoria, y centrar nuestra atención en el conjunto de valores que puede tomar.

Funciones de distribución de probabilidad

De manera general, existe un tipo de función que nos va a interesar a partir de ahora, que corresponde a las funciones de distribución de probabilidad. Estas se definen como sigue.

---

Definición. Sea $F:\mathbb{R}\to \mathbb{R}$ una función. Diremos que $F$ es una función de distribución de probabilidad si:

1. $F$ es no-decreciente. Esto es, para cada $a,b\in \mathbb{R}$, si $a<b$ entonces $F(a)\le F(b)$.
2. $F$ es continua por la derecha. Es decir, para cada $a\in \mathbb{R}$ se cumple que$$\underset{x\to a^{+}}{lim}F(x)=F(a).$$
3. Se cumple que$$\underset{x\to \mathrm{\infty }}{lim}F(x)=1\text{y}\underset{x\to -\mathrm{\infty }}{lim}F(x)=0.$$

---

Una función no requiere de ningún contexto adicional para considerarse una función de distribución de probabilidad. Es decir, para que una función $F:\mathbb{R}\to \mathbb{R}$ sea considerada una función de distribución de probabilidad, simplemente debe de ser no-decreciente, continua por la derecha y sus límites a $\mathrm{\infty }$ y $-\mathrm{\infty }$ deben de ser $1$ y $0$, respectivamente.

Ejemplo 1. Sean $a,b\in \mathbb{R}$ tales que $a<b$. La función $F:\mathbb{R}\to \mathbb{R}$ dada por

$$F(x)=\{\begin{array}{ll}0& \text{si }x<a\text{,}\\ \frac{x-a}{b-a}& \text{si }a\le x\le b\text{,}\\ 1& \text{si }b<x\text{.}\end{array}$$

es no-decreciente, continua por la derecha y sus límites a $\mathrm{\infty }$ y $-\mathrm{\infty }$ son $1$ y $0$, así que es una función de distribución de probabilidad. Gráficamente, se ve como sigue.

---

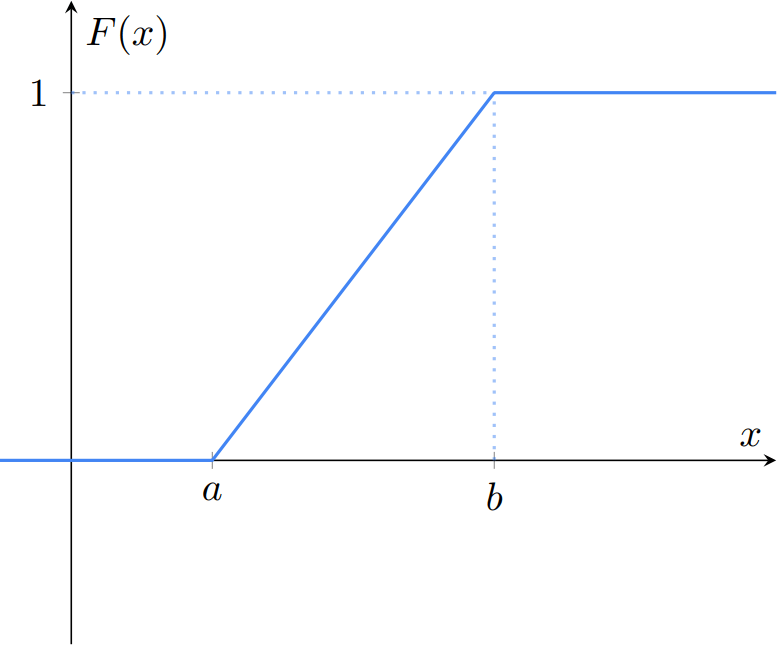
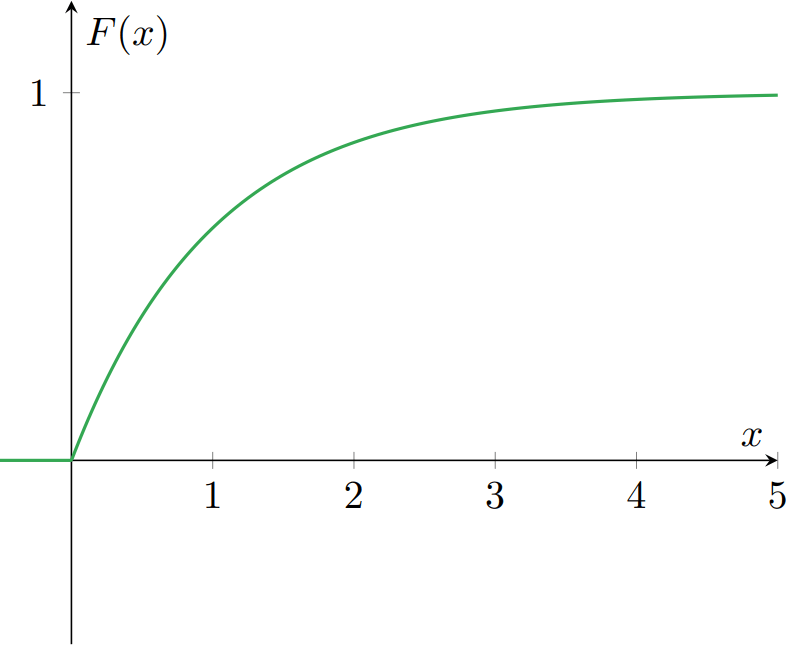
Ejemplo 2. Sea $\lambda \in \mathbb{R}$ tal que $\lambda >0$. La función $F:\mathbb{R}\to \mathbb{R}$ dada por

$$F(x)=\{\begin{array}{ll}0& \text{si }x<0\text{,}\\ 1-e^{-\lambda x}& \text{si }x\ge 0\text{.}\end{array}$$

es una función de distribución de probabilidad. Gráficamente:

---

Función de distribución de una variable aleatoria

Dada cualquier variable aleatoria $X$ sobre un espacio de probabilidad $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$, hay una función muy importante asociada a $X$: su función de distribución, definida como sigue.

---

Definición. Sea $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$ un espacio de probabilidad y sea $X:\mathrm{\Omega }\to \mathbb{R}$ una variable aleatoria. La función de distribución de $X$ es la función $F_X:\mathbb{R}\to [0,1]$ dada por

$$F_X(x)=\mathbb{P}(\{\omega \in \mathrm{\Omega }\mid X(\omega )\le x\})=\mathbb{P}(X\le x),\text{para cada }x\in \mathbb{R}.$$

$F_X$ también es llamada la función de distribución acumulada de $X$, que en inglés se abrevia como CDF (cumulative distribution function).

---

Es decir, dada una variable aleatoria $X$, su función de distribución devuelve la probabilidad de que $X$ sea menor o igual a $x$, para cada $x\in \mathbb{R}$. Como seguramente ya sospechas por el nombre de $F_X$, resulta que $F_X$ es una función de distribución de probabilidad. Este hecho es demostrado en el siguiente teorema.

---

Teorema. Sea $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$ un espacio de probabilidad y sea $X:\mathrm{\Omega }\to \mathbb{R}$ una variable aleatoria. Entonces $F_X:\mathbb{R}\to [0,1]$ es una función de distribución de probabilidad.

---

Demostración. De acuerdo con la definición, para demostrar que $F_X:\mathbb{R}\to \mathbb{R}$ es una función de distribución de probabilidad, tenemos que demostrar 3 cosas:

1. $F_X$ es no-decreciente: para cada $a,b\in \mathbb{R}$, si $a<b$ entonces $F_X(a)\le F_X(b)$.
2. $F_X$ es continua por la derecha: que para cada $a\in \mathbb{R}$ se cumple que$$\underset{x\to a^{+}}{lim}{F}_X(x)=F_X(a).$$
3. Se cumple que$$\underset{x\to \mathrm{\infty }}{lim}{F}_X(x)=1\text{y}\underset{x\to -\mathrm{\infty }}{lim}{F}_X(x)=0.$$

Veamos que se cumple 1. Sean $a,b\in \mathbb{R}$ tales que $a<b$. Ahora, observa que $(a,b]=(-\mathrm{\infty },b]\setminus (-\mathrm{\infty },a]$, por lo que

$$\begin{array}{rl}\mathbb{P}(X^{-1}[(a,b]])& =\mathbb{P}(X^{-1}[(-\mathrm{\infty },b]\setminus (-\mathrm{\infty },a]])\\ & =\mathbb{P}(X^{-1}[(-\mathrm{\infty },b]]\setminus X^{-1}[(-\mathrm{\infty },a]]).\end{array}$$

Como $a<b$, se cumple que $(-\mathrm{\infty },a]\subseteq (-\mathrm{\infty },b]$, por lo que

$$X^{-1}[(-\mathrm{\infty },a]]\subseteq X^{-1}[(-\mathrm{\infty },b]],$$

así que $\mathbb{P}(X^{-1}[(-\mathrm{\infty },b]]\setminus X^{-1}[(-\mathrm{\infty },a]])=\mathbb{P}(X^{-1}[(-\mathrm{\infty },b]])-\mathbb{P}(X^{-1}[(-\mathrm{\infty },a]])$. En consecuencia, tenemos que

$$\begin{array}{rl}\mathbb{P}(X^{-1}[(a,b]])& =\mathbb{P}(X^{-1}[(-\mathrm{\infty },b]])-\mathbb{P}(X^{-1}[(-\mathrm{\infty },a]])\\ & =\mathbb{P}(X\le b)-\mathbb{P}(X\le a)\\ & =F_X(b)-F_X(a).\end{array}$$

Recuerda que $\mathbb{P}$ es una medida de probabilidad, por lo que $\mathbb{P}(X^{-1}[(a,b]])\ge 0$; que implica $F_X(b)-F_X(a)\ge 0$, o equivalentemente, que $F_X(b)\ge F_X(a)$. En conclusión, para cualesquiera $a,b\in \mathbb{R}$ tales que $a<b$, se cumple que $F_X(a)\le F_X(b)$, que es justamente lo que queríamos demostrar. Por lo tanto, $F_X$ es una función no-decreciente.

Para demostrar 2, sea $(x_n{)}_{n\in {\mathbb{N}}^{+}}\subseteq \mathbb{R}$ una sucesión monótona decreciente de números reales tal que su límite es $0$. Es decir, $x_1>x_2>x_3>\cdots$ y

$$\underset{n\to \mathrm{\infty }}{lim}{x}_n=0.$$

Ahora, sea $a\in \mathbb{R}$. Definimos la sucesión de eventos $\{A_n{\}}_{n\in {\mathbb{N}}^{+}}$ tal que para cada $n\in {\mathbb{N}}^{+}$, $A_n=(X\le a+x_n)$. De este modo, se tiene que

$$\bigcap _{n=1}^{\mathrm{\infty }}{A}_n=(X\le a),$$

pues la sucesión $(x_n{)}_{n\in {\mathbb{N}}^{+}}$ converge a $0$. Ahora, por el teorema de continuidad de la probabilidad, tenemos que

$$F_X(a)=\mathbb{P}(X\le a)=\mathbb{P}\left(\bigcap _{n=1}^{\mathrm{\infty }}{A}_n\right)=\underset{n\to \mathrm{\infty }}{lim}\mathbb{P}\left(A_n\right)=\underset{n\to \mathrm{\infty }}{lim}\mathbb{P}(X\le a+x_n)=\underset{n\to \mathrm{\infty }}{lim}{F}_X(a+x_n),$$

es decir, $\underset{n\to \mathrm{\infty }}{lim}{F}_X(a+x_n)=F_X(a)$, para cualquier $a\in \mathbb{R}$ y cualquier sucesión monótona decreciente $(x_n{)}_{n\in {\mathbb{N}}^{+}}$. Por ello, se puede concluir que $F_X$ es una función continua por la derecha.

Finalmente, en 3 demostraremos que el límite de $F_X(x)$ cuando $x\to \mathrm{\infty }$ es $1$. La demostración del otro límite es muy parecida. Sea $(x_n{)}_{n\in {\mathbb{N}}^{+}}\subseteq \mathbb{R}$ una sucesión de números reales tal que $x_1\le x_2\le x_3\le \cdots$ y $\underset{n\to \mathrm{\infty }}{lim}{x}_n=\mathrm{\infty }$. Para cada $n\in {\mathbb{N}}^{+}$ definimos

$$A_n=(X\le x_n)=X^{-1}[(-\mathrm{\infty },x_n]].$$

De esta forma, tenemos que $\{A_n{\}}_{n\in {\mathbb{N}}^{+}}$ es una sucesión creciente de eventos, pues observa que $A_1\subseteq A_2\subseteq A_3\subseteq \cdots$ De este modo, como supusimos que $(x_n{)}_{n\in {\mathbb{N}}^{+}}$ es una sucesión que diverge a $\mathrm{\infty }$, se tiene que

$$\bigcup _{n=1}^{\mathrm{\infty }}{A}_n=\bigcup _{n=1}^{\mathrm{\infty }}(X\le x_n)=\bigcup _{n=1}^{\mathrm{\infty }}{X}^{-1}[(-\mathrm{\infty },x_n]]=X^{-1}[\bigcup _{n=1}^{\mathrm{\infty }}(-\mathrm{\infty },x_n]]=X^{-1}[\mathbb{R}]=\mathrm{\Omega }.$$

Ahora, aplicando el teorema de la continuidad de la probabilidad a $\{A_n{\}}_{n\in {\mathbb{N}}^{+}}$ y usando que la sucesión $(x_n{)}_{n\in {\mathbb{N}}^{+}}$ es divergente, tenemos que

$$\begin{array}{rl}\underset{x\to \mathrm{\infty }}{lim}{F}_X(x)& =\underset{n\to \mathrm{\infty }}{lim}{F}_X(x_n)\\ & =\underset{n\to \mathrm{\infty }}{lim}\mathbb{P}(X\le x_n)\\ & =\underset{n\to \mathrm{\infty }}{lim}\mathbb{P}\left(A_n\right)\\ & =\mathbb{P}\left(\bigcup _{n=1}^{\mathrm{\infty }}{A}_n\right)\\ & =\mathbb{P}\left(\mathrm{\Omega }\right)\\ & =1.\end{array}$$

En conclusión, tenemos que

$$\underset{x\to \mathrm{\infty }}{lim}{F}_X(x)=1,$$

que es justamente lo que queríamos demostrar. La demostración de que el límite a $-\mathrm{\infty }$ de $F_X$ es $0$ se obtiene de manera casi análoga, pero la familia de eventos que se plantea es decreciente, y se utiliza el teorema de continuidad de la probabilidad para ese caso.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Partiendo de una función de distribución de probabilidad

Por el teorema anterior, vimos que la función de distribución de cualquier variable aleatoria es también una función de distribución de probabilidad. Es decir, que si tienes un espacio de probabilidad $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$ y una variable aleatoria $X:\mathrm{\Omega }\to \mathbb{R}$, la función de distribución de $X$, $F_X:\mathbb{R}\to [0,1]$, es una función de distribución de probabilidad.

Por otro lado, ahora imagina que te encuentras con una función $F:\mathbb{R}\to \mathbb{R}$ que es una función de distribución de probabilidad. No obstante, observa que no sabes nada más sobre esta función. Es decir, no hay ninguna variable aleatoria ni un espacio de probabilidad a la vista… ¿Será posible que $F$ provenga de alguna variable aleatoria $X$ definida sobre un espacio de probabilidad $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$?

En otras palabras: dada $F:\mathbb{R}\to \mathbb{R}$ una función de distribución de probabilidad, ¿siempre existen un espacio de probabilidad $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$ y una variable aleatoria $X:\mathrm{\Omega }\to \mathbb{R}$ tal que $F$ es la función de distribución de $X$? ¡La respuesta es que sí! A grandes rasgos, $F$ define la probabilidad de los eventos de la forma $(-\mathrm{\infty },x]$, para cada $x\in \mathbb{R}$. Esto resulta suficiente para definir por completo la medida de probabilidad inducida por una variable aleatoria $X$… pero, ¿cuál variable aleatoria $X$? De manera canónica, siempre puede utilizarse la variable aleatoria identidad sobre $\mathrm{\Omega }=\mathbb{R}$, que es la función $X:\mathbb{R}\to \mathbb{R}$ tal que para cada $\omega \in \mathbb{R}$, $X(\omega )=\omega$. De este modo, la medida de probabilidad inducida por $X$ es la misma que la medida en el dominio de $X$, que en este caso es $\mathbb{R}$ con $\mathcal{B}(\mathbb{R})$ como σ-álgebra, y usando la medida determinada por $F$.

¡CUIDADO! Esto NO significa que todas las variables aleatorias son simplemente la función identidad. Lo que significa es que siempre que tengas una función de distribución de probabilidad $F:\mathbb{R}\to \mathbb{R}$, está garantizado que existen un espacio de probabilidad $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$ y una variable aleatoria $X:\mathrm{\Omega }\to \mathbb{R}$ de tal forma que $F$ es la función de distribución de $X$. La existencia está garantizada porque, al menos, siempre se puede usar la función identidad de $\mathbb{R}$ en $\mathbb{R}$ como variable aleatoria, pero puede haber otras distintas cuya función de distribución también es $F$.

Los siguientes ejemplos son largos, pero capturan muchas de las ideas vistas hasta ahora sobre variables aleatorias. Además, en conjunto, estos dos ejemplos exhiben lo que comentamos en el párrafo anterior.

Ejemplo 3. Sea $\mathrm{\Omega }=\{0,1{\}}^3$. Es decir, $\mathrm{\Omega }$ es el conjunto

$$\mathrm{\Omega }=\{(0,0,0),(0,0,1),(0,1,0),(1,0,0),(0,1,1),(1,0,1),(1,1,0),(1,1,1)\}.$$

$\mathrm{\Omega }$ puede pensarse como el espacio muestral de un experimento aleatorio en el que se hacen $3$ ensayos de un experimento aleatorio que tiene dos resultados posibles: éxito o fracaso. Por ejemplo, el lanzamiento de una moneda («águila» o «sol»). Tomaremos como σ-algebra de $\mathrm{\Omega }$ a $\mathcal{P}(\mathrm{\Omega })$, la potencia de $\mathrm{\Omega }$.

Sea $p\in \mathbb{R}$ tal que $p\in [0,1]$. Plantearemos una medida de probabilidad tal que los $3$ ensayos son independientes. Para ello, para cada $k\in \{1,2,3\}$ planteamos los eventos

• $A_k$: el evento de que el $k$-ésimo ensayo sea un éxito. Es decir, $A_k$ es el evento$$A_k=\{({\omega }_1,{\omega }_2,{\omega }_3)\in \mathrm{\Omega }\mid {\omega }_k=1\}.$$
• $B_k$: el evento de que el $k$-ésimo ensayo sea un fracaso. Es decir, $B_k$ es el evento$$B_k=\{({\omega }_1,{\omega }_2,{\omega }_3)\in \mathrm{\Omega }\mid {\omega }_k=0\}.$$

Observa que para cada $k\in \{1,2,3\}$ se cumple que $B_k=A_k^{\mathsf{c}}$. Por ejemplo, $A_2$ es el evento

$$A_2=\{({\omega }_1,{\omega }_2,{\omega }_3)\in \mathrm{\Omega }\mid {\omega }_2=1\}=\{(0,1,0),(0,1,1),(1,1,0),(1,1,1)\}$$

Comenzamos a definir la medida de probabilidad $\mathbb{P}:\mathcal{P}(\mathrm{\Omega })\to \mathbb{R}$ como sigue: para cada $k\in \{1,2,3\}$ definimos

y pedimos que $\mathbb{P}$ sea tal que los eventos $A_1$, $A_2$ y $A_3$ son independientes. En consecuencia, se cumple lo siguiente

$$\begin{array}{}\text{(1)}& \mathbb{P}(A_1\cap A_2\cap A_3)& =\mathbb{P}\left(A_1\right)\mathbb{P}\left(A_2\right)\mathbb{P}\left(A_3\right)=p^3\text{(2)}& \mathbb{P}(B_1\cap A_2\cap A_3)& =\mathbb{P}\left(B_1\right)\mathbb{P}\left(A_2\right)\mathbb{P}\left(A_3\right)=(1-p)p^2=p^2(1-p)\text{(3)}& \mathbb{P}(A_1\cap B_2\cap A_3)& =\mathbb{P}\left(A_1\right)\mathbb{P}\left(B_2\right)\mathbb{P}\left(A_3\right)=p(1-p)p=p^2(1-p)\text{(4)}& \mathbb{P}(A_1\cap A_2\cap B_3)& =\mathbb{P}\left(A_1\right)\mathbb{P}\left(A_2\right)\mathbb{P}\left(B_3\right)=p^2(1-p),\text{(5)}& \mathbb{P}(B_1\cap B_2\cap A_3)& =\mathbb{P}\left(B_1\right)\mathbb{P}\left(B_2\right)\mathbb{P}\left(A_3\right)=(1-p{)}^{2}p=p(1-p{)}^2,\text{(6)}& \mathbb{P}(B_1\cap A_2\cap B_3)& =\mathbb{P}\left(B_1\right)\mathbb{P}\left(A_2\right)\mathbb{P}\left(B_3\right)=(1-p)p(1-p)=p(1-p{)}^2,\text{(7)}& \mathbb{P}(A_1\cap B_2\cap B_3)& =\mathbb{P}\left(A_1\right)\mathbb{P}\left(B_2\right)\mathbb{P}\left(B_3\right)=p(1-p{)}^2,\text{(8)}& \mathbb{P}(B_1\cap B_2\cap B_3)& =\mathbb{P}\left(B_1\right)\mathbb{P}\left(B_2\right)\mathbb{P}\left(B_3\right)=(1-p{)}^3.\end{array}$$

De hecho, observa que estas condiciones son suficientes para definir la probabilidad de cada resultado, y así, la de cada evento $A\in \mathcal{P}(\mathrm{\Omega })$. Por ejemplo, nota que

$$A_1\cap A_2\cap A_3=\{({\omega }_1,{\omega }_2,{\omega }_3)\in \mathrm{\Omega }\mid {\omega }_1=1\wedge {\omega }_2=1\wedge {\omega }_3=1\}=\{(1,1,1)\},$$

y por lo anterior, $\mathbb{P}(A_1\cap A_2\cap A_3)=p^3$. Por lo tanto, se concluye que

$$\mathbb{P}(\{(1,1,1)\})=p^3.$$

Los $8$ elementos de $\mathrm{\Omega }$ pueden verse como las intersecciones de las identidades $(1)$ a $(8)$, así que la probabilidad de cada uno está determinada por cada una de esas igualdades. Por ejemplo, además de la anterior ($\mathbb{P}(\{(1,1,1)\})=p^3$), observa que

$$A_1\cap B_2\cap B_3=\{({\omega }_1,{\omega }_2,{\omega }_3)\in \mathrm{\Omega }\mid {\omega }_1=1\wedge {\omega }_2=0\wedge {\omega }_3=0\}=\{(1,0,0)\},$$

por lo que $\mathbb{P}(\{(1,0,0)\})=p(1-p{)}^2$. Ahora, presta atención a los exponentes de $p$ y de $1-p$ en estas probabilidades, y compáralos con el número de $1$’s y $0$’s de las ternas ordenadas. ¿Qué puedes observar? Resulta que el exponente de la $p$ es el número de $1$’s, es decir, el número de éxitos. Por otro lado, el exponente del $1-p$ es el número de $0$’s, es decir, el número de fracasos.

Ahora, para cada $\mathbf{a}\in \mathrm{\Omega }$, $\mathbf{a}$ puede escribirse como $\mathbf{a}=(a_1,a_2,a_3)$, con $a_1$, $a_2$, $a_3\in \{0,1\}$. En consecuencia, el número de éxitos en la terna $\mathbf{a}$ puede escribirse como

$${\Vert \mathbf{a}\Vert }_1={\Vert (a_1,a_2,a_3)\Vert }_1=|a_1|+|a_2|+|a_3|.$$

Por el contrario, el número de fracasos en la terna $\mathbf{a}$ puede escribirse como

$$3-{\Vert \mathbf{a}\Vert }_1=3-{\Vert (a_1,a_2,a_3)\Vert }_1=3-(|a_1|+|a_2|+|a_3|).$$

De este modo, para cada $\mathbf{a}\in \mathrm{\Omega }$, se tiene que

$$\mathbb{P}(\{\mathbf{a}\})=p^{{\Vert \mathbf{a}\Vert }_1}(1-p{)}^{3-{\Vert \mathbf{a}\Vert }_1}.$$

Por esta razón, definimos a la medida de probabilidad $\mathbb{P}:\mathcal{P}(\mathrm{\Omega })\to \mathbb{R}$ dada por

$$\mathbb{P}\left(A\right)=\sum _{\mathbf{a}\in A}{p}^{{\Vert \mathbf{a}\Vert }_1}(1-p{)}^{3-{\Vert \mathbf{a}\Vert }_1},\text{para cada }A\in \mathcal{P}(\mathrm{\Omega })\text{.}$$

Ahora, definimos a la variable aleatoria $X:\mathrm{\Omega }\to \mathbb{R}$ como sigue. Para cada $\mathbf{a}\in \mathrm{\Omega }$, se define

$$X(\mathbf{a})=\Vert \mathbf{a}{\Vert }_1,$$

por lo que si $\mathbf{a}=(a_1,a_2,a_3)$, se tiene que

$$X(\mathbf{a})=|a_1|+|a_2|+|a_3|.$$

Por ejemplo, $X(1,0,1)=1+0+1=2$, y $X(1,1,1)=1+1+1=3$. Es decir, $X$ contabiliza el número de éxitos en los $3$ ensayos. Observa que el conjunto de valores que puede tomar $X$ es $\{0,1,2,3\}$. Obtengamos la probabilidad de que $X$ tome cada uno de estos valores.

$$\begin{array}{rl}\mathbb{P}(X=0)=\mathbb{P}(\{\omega \in \mathrm{\Omega }\mid X(\omega )=0\})& =\mathbb{P}(\{(0,0,0)\})\\ & =(1-p{)}^3,\\ \mathbb{P}(X=1)=\mathbb{P}(\{\omega \in \mathrm{\Omega }\mid X(\omega )=1\})& =\mathbb{P}(\{(1,0,0),(0,1,0),(0,0,1)\})\\ & =p(1-p{)}^2+p(1-p{)}^2+p(1-p{)}^2\\ & =3p(1-p{)}^2,\\ \mathbb{P}(X=2)=\mathbb{P}(\{\omega \in \mathrm{\Omega }\mid X(\omega )=2\})& =\mathbb{P}(\{(1,1,0),(1,0,1),(0,1,1)\})\\ & =p^2(1-p)+p^2(1-p)+p^2(1-p)\\ & =3p^2(1-p),\\ \mathbb{P}(X=3)=\mathbb{P}(\{\omega \in \mathrm{\Omega }\mid X(\omega )=3\})& =\mathbb{P}(\{(1,1,1)\})\\ & =p^3.\end{array}$$

Ahora obtengamos la función de distribución de $X$. Esto es,

$$F_X(x)=\mathbb{P}(X\le x).$$

Primero, observa que para cada $x\in (-\mathrm{\infty },0)$ se tiene que $F_X(x)=0$, pues la variable aleatoria no toma valores negativos. Después,

$$F_X(0)=\mathbb{P}(X\le 0)=\mathbb{P}(\{\omega \in \mathrm{\Omega }\mid X(\omega )\le 0\})=\mathbb{P}(\{(0,0,0)\})=(1-p{)}^3.$$

Por otro lado, para cada $x\in (0,1)$, observa que

$$F_X(x)=\mathbb{P}(X\le x)=\mathbb{P}(\{\omega \in \mathrm{\Omega }\mid X(\omega )\le x\})=\mathbb{P}(\{(0,0,0)\}).$$

porque el único $\omega \in \mathrm{\Omega }$ que hace que $X(\omega )\le x$ es $\omega =(0,0,0)$, para todos los demás, $X(\omega )$ vale al menos $1$, que es mayor a $x$. Luego, tenemos que

$$\begin{array}{rl}{F}_X(1)=\mathbb{P}(X\le 1)& =\mathbb{P}(\{\omega \in \mathrm{\Omega }\mid X(\omega )\le 1\})\\ & =\mathbb{P}(\{(0,0,0),(0,0,1),(0,1,0),(1,0,0)\})\\ & =(1-p{)}^3+3p(1-p{)}^2,\end{array}$$

Observa que ahí se acumularon los elementos de $\mathrm{\Omega }$ que hacen que $X(\omega )=0$ y $X(\omega )=1$, pues son todos los valores que toma la variable aleatoria que son menores o iguales a $1$.

Después, para cada $x\in (1,2)$, los $\omega \in \mathrm{\Omega }$ que hacen que $X(\omega )\le x$ son los mismos que en el caso anterior, por lo que $F_X(x)=F_X(1)$. Continuando de esta manera, se llega a que

$$\begin{array}{rl}{F}_X(2)& =(1-p{)}^3+3p(1-p{)}^2+3p^2(1-p),\\ F_X(x)& =F_X(2)& \text{para cada }x\in (2,3)\text{,}\\ F_X(3)& =(1-p{)}^3+3p(1-p{)}^2+3p^2(1-p)+p^3,\\ F_X(x)& =F_X(3)& \text{para cada }x\in (3,\mathrm{\infty })\text{.}\end{array}$$

Observa que la expresión para $F_X(3)$ corresponde a $(p+(1-p){)}^3$, por el teorema del binomio. En consecuencia, $F_X(3)=(p+(1-p){)}^3=1^3=1$. De este modo, obtenemos que la función de distribución de $X$ es la función dada por

$$F_X(x)=\{\begin{array}{ll}0& \text{si }x<0\text{,}\\ (1-p{)}^3& \text{si }0\le x<1\text{,}\\ (1-p{)}^3+3p(1-p{)}^2& \text{si }1\le x<2\text{,}\\ (1-p{)}^3+3p(1-p{)}^2+3p^2(1-p)& \text{si }2\le x<3\text{,}\\ 1& \text{si }3\le x\text{.}\end{array}$$

Nota que a pesar de ser una función con discontinuidades (es una función escalonada), $F_X$ sí es continua por la derecha. Observa que también es no-decreciente, y sus límites a $-\mathrm{\infty }$ y a $\mathrm{\infty }$ son $0$ y $1$, respectivamente; algo que ya esperábamos por el teorema demostrado en esta entrada.

---

Ejemplo 4. Ahora sea $F:\mathbb{R}\to \mathbb{R}$ la siguiente función de distribución de probabilidad:

$$F(x)=\{\begin{array}{ll}0& \text{si }x<0\text{,}\\ (1-p{)}^3& \text{si }0\le x<1\text{,}\\ (1-p{)}^3+3p(1-p{)}^2& \text{si }1\le x<2\text{,}\\ (1-p{)}^3+3p(1-p{)}^2+3p^2(1-p)& \text{si }2\le x<3\text{,}\\ 1& \text{si }3\le x\text{.}\end{array}$$

¡Es la función de distribución de la variable aleatoria $X$ del ejemplo pasado! Sin embargo, nota que aquí te la estamos dando sin ninguna información sobre el espacio de probabilidad subyacente, ni sobre la variable aleatoria involucrada. En primer lugar, ya tenemos garantizado que existe el espacio de probabilidad $(\{0,1{\}}^3,\mathcal{P}(\{0,1{\}}^3),\mathbb{P})$ y la variable aleatoria $X:\{0,1{\}}^3\to \mathbb{R}$ dada por $X(\omega )={\Vert \omega \Vert }_1$, para cada $\omega \in \{0,1{\}}^3$ de tal forma que $F$ es la función de distribución de $X$.

No obstante, observa que podemos definir otra variable aleatoria que resulta en la misma función de distribución. Para ello, toma a $(\mathbb{R},\mathcal{B}(\mathbb{R}),\mathbb{P})$, donde $\mathbb{P}$ es la medida de probabilidad $\mathbb{P}:\mathcal{B}(\mathbb{R})\to \mathbb{R}$ definida como sigue: para cada $x\in \mathbb{R}$, definimos

$$\mathbb{P}((-\mathrm{\infty },x])=F(x).$$

Ojo: Esto define la probabilidad de los elementos de $\mathcal{B}(\mathbb{R})$ (que son eventos) que tienen la forma $(-\mathrm{\infty },x]$, para cada $x\in \mathbb{R}$. A su vez, esto define la probabilidad de los eventos de la forma $(a,b]$, para cada $a$, $b\in \mathbb{R}$ tales que $a<b$, que es

$$\mathbb{P}((a,b])=F(b)-F(a),$$

que se puede extender de manera única a una medida sobre todo $\mathcal{B}(\mathbb{R})$. Esto es algo que puede demostrarse, pero carecemos de las herramientas para hacerlo en este curso. De cualquier modo, la variable aleatoria que utilizamos en este caso es $Y:\mathbb{R}\to \mathbb{R}$, la función identidad, dada por

$$Y(\omega )=\omega ,\text{para cada }\omega \in \mathbb{R}\text{.}$$

De este modo, se tiene que

$$\begin{array}{rl}(Y\le y)& =\{\omega \in \mathbb{R}\mid Y(\omega )\le y\}\\ & =\{\omega \in \mathbb{R}\mid \omega \le y\}\\ & =(-\mathrm{\infty },y],\end{array}$$

y por lo tanto, para cada $y\in \mathbb{R}$,

$$F_Y(y)=\mathbb{P}(Y\le y)=\mathbb{P}((-\mathrm{\infty },y])=F(y),$$

por lo que la función de distribución de $Y$ es precisamente la función de distribución de probabilidad que escogimos al comenzar este ejemplo. De este modo, $Y$ es una variable aleatoria que puede tomar los valores $0$, $1$, $2$ y $3$… ¡con las mismas probabilidades que la variable aleatoria $X$ del ejemplo pasado! Sin embargo, ¡los espacios de probabilidad sobre los que estas están definidas son completamente distintos! Esto exhibe que lo más importante de una variable aleatoria es su función de distribución, pues esta determina los valores que puede tomar, y la probabilidad con la que los toma. Es decir, la función de distribución caracteriza el comportamiento probabilístico de una variable aleatoria.

---

¡Presta mucha atención a los últimos dos ejemplos! La conclusión es que el espacio de probabilidad que subyace a una variable aleatoria realmente no importa. Por ello, en muchos libros de probabilidad (y en este mismo curso), no le prestan atención a esto. Comúnmente, te dan una función $F$ que es una función de distribución de probabilidad, y te dicen «sea $X$ una variable aleatoria con distribución $F$». Con eso es suficiente, pues $F$ determina las probabilidades de todos los eventos que involucran a $X$, sin importar quiénes son $X$ y el espacio de probabilidad sobre el que ésta se define.

Tarea moral

Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.

1. Determina si la función $F:\mathbb{R}\to \mathbb{R}$ dada por$$F(x)=\{\begin{array}{ll}0& \text{si }x\le -1\text{,}\\ \frac{1}{2}(x+1{)}^2& \text{si }-1<x\le 0\text{,}\\ 1-\frac{1}{2}(1-x{)}^2& \text{si }0<x<1\text{,}\\ 1& \text{si }x\ge 1\end{array}$$es una función de distribución de probabilidad. Utiliza su gráfica para auxiliarte, en caso de que lo necesites.
2. Demuestra que el límite a $-\mathrm{\infty }$ de la función de distribución de una variable aleatoria es $0$ Sugerencia: Revisa la demostración de la propiedad 3 que vimos en el teorema de esta entrada.
3. ¿Podrías idear más variables que tengan la misma función de distribución del Ejemplo 3? Por ejemplo, si ${\mathrm{\Omega }}_2=\{0,2{\}}^3$, decimos que $2$ representa éxito; y definimos $Z:{\mathrm{\Omega }}_2\to \mathbb{R}$ como la función dada por$$\begin{array}{rlr}Z({\omega }_1,{\omega }_2,{\omega }_3)& =\frac{{\omega }_1+{\omega }_2+{\omega }_3}{2}& \text{para cada }({\omega }_1,{\omega }_2,{\omega }_3)\in {\mathrm{\Omega }}_2\text{,}\end{array}$$¿tiene $Z$ la misma distribución que la $X$ del Ejemplo 3?

Más adelante…

Lo siguiente que haremos en el curso es ver los dos tipos de variables aleatorias más importantes que hay, las discretas y las continuas. A grandes rasgos, las discretas son aquellas que pueden tomar una cantidad a lo más numerable de valores distintos, mientras que las continuas son aquellas que pueden tomar una cantidad no-numerable de valores. Es decir, pueden tomar valores en un conjunto cuya cardinalidad es igual a la de $\mathbb{R}$. En la siguiente entrada abordaremos las particularidades de las variables aleatorias discretas.

Entradas relacionadas

• Ir a Probabilidad I
• Entrada anterior del curso: Variables Aleatorias
• Siguiente entrada del curso: Variables Aleatorias Discretas