$\textcolor{Red}{\textbf{Extremos Restringidos (Multiplicadores de Lagrange)}}$

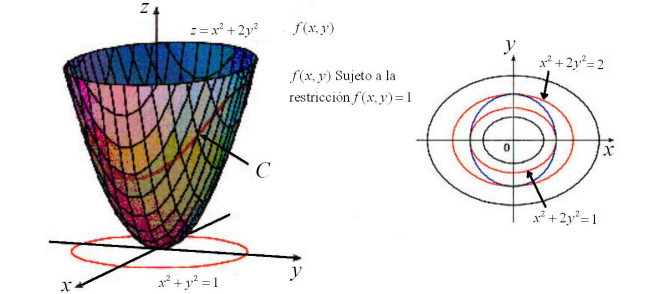
Supongase que se quieren hallar los valores extremos (máximo ó mínimo) de una función $f(x,y)$ sujeta a la restircción $x^2+y^2=1$; esto es, que $(x,y)$ está en el circulo unitario. Con mayor generalidad, podemos necesitar maximizar o minimizar $f(x,y)$ sujeta a la condición adicional de que $(x,y)$ también satisfaga una ecuación $g(x,y)=c$ donde $g$ es alguna función y $c$ es una constante. En el ejemplo $g(x,y)=x^2+y^2$ y $c=1$]. El conjunto de dichas $(x,y)$ es un conjunto de nivel de $g$.

En general, sean $f:u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ y $g: u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ funciones $C^1$ dadas, y sea $S$ el conjunto de nivel de $g$ con valor $c$. Recordar que el conjunto de nivel son los puntos $x\in
\mathbb{R}^n$ con $g(x)=c$] Cuando $f$ se restringe a $S$, de nuevo tenemos el concepto de máximos locales o mínimos locales de $f$ (extremos locales), y un máximo (valor mayor) o un minimo absoluto (valor menor) debe ser un extremo local.

$\textbf{Teorema.- Método de los multiplicadores de lagrange.}$ Sean $f:u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ y $g: u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ funciones $C^1$ con valores reales dados. Sean $x_0 \in u$ y $g(x_0)=c$, y sea $S$ el conjunto de nivel de $g$ con valor $c$. Suponer $\nabla g(x_0)\neq 0$.
Si $f|_s$ (f restringida a s) tiene un máximo o un mínimo local en $S$, en $x_0$, entonces existe un número real $\lambda$ tal que $\nabla f(x_0)=\lambda\nabla g(x_0)$.

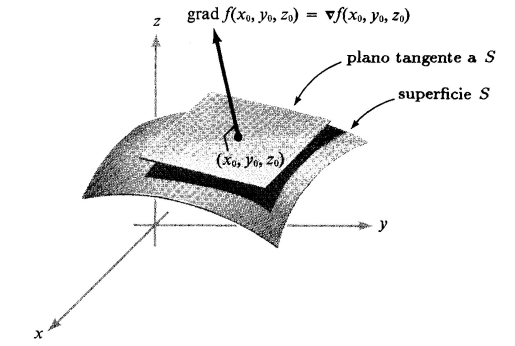
$Demostrción$ Para $n=3$ el espacio tangente o plano tangente de $S$ en $x_0$ es el
espacio ortogonal a $\nabla g(x_0)$ y para $n$ arbitraria podemos dar la misma definición de espacio tangente de $S$ en $x_0$. Esta definición se puede motivar al considerar tangentes a trayectorias $c(t)$ que estan en $s$, como sigue: si $c(t)$ es una trayectoria en $S$ y $c(0)=x_0$, entonces $c'(0)$ es un vector tangente a $S$ en $x_0$, pero $$\frac{dg(c(t))}{dt}=\frac{d}{dt}(c)=0$$
Por otro lado usando regla de la cadena
$$\left.\frac{d}{dt}g(c(t))\right|_{t=0}=\nabla g(x_0)\cdot c'(0)$$
de manera que $\nabla g(x_0)\cdot c'(0)=0$, esto es, $c'(0)$ es ortogonal a $\nabla g(x_0)$.

Si $f|s$ tiene un máximo en $x_0$, entonces $f(c(t))$ tiene un máximo en $t=0$. Por cálculo de una variable, $\displaystyle\left.\frac{df(c(t))}{dt}\right|{t=0}=0$. Entonces por regla de la cadena $$0=\displaystyle\left.\frac{df(c(t))}{dt}\right|_{t=0}=\nabla f(x_0)\cdot c'(0)$$
Asi, $\nabla f(x_0)$ es perpendicular a la tangente de toda curva en $S$ y entonces tambien es perpendicular al espacio tangente completo de $S$ en $x_0$. Como el espacio perpendicular a este espacio tangente es una recta, $\nabla f(x_0)$ y $\nabla
g(x_0)$ son paralelos. Como $\nabla g(x_0)\neq 0$, se deduce que $\nabla f(x_0)$ es multiplo de $\nabla g(x_0)$.

$\textbf{Corolario.}$ Si $f$ al restringirse a una superficie $S$, tiene un máximo o un mínimo local en $x_0$, entonces $\nabla f(x_0)$ es perpendicular a $S$ en $x_0$.La geometria de los valores extremos restringidos.

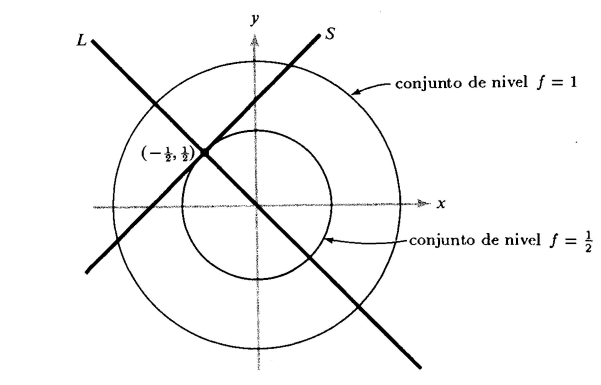
$\textbf{Ejemplo.}$ Sea $S\subset\mathbb{R}^2$ la recta que pasa por $(-1,0)$ inclinada a $45^{o}$, y sea $f:\mathbb{R}^2 \rightarrow \mathbb{R}$ daa asi $f(x,y)=x^2+y^2$. Hallar los extremos de $f|_s$.

$Solución.$ Aqui $S=\left\{(x,y) | y-x-1=0 \right\}$ y por lo tanto hacemos $g(x,y)=-y-x-1$ y $c=0$. Tenemos $\nabla g(x,y)=-i+j \neq 0$. Los extremos relativos de $f|_s$ deben hallarse entre los puntos en que $\nabla f$ es ortogonal a $S$, esto es, inclinada a $-45^{o}$. Pero $\nabla f (x,y)=(2x.2y)$, que tiene la pendiente deseada sólo cuando $x=-y$, o cuando $(x,y)$ está sobre la recta L, que pasa por el origen inlinada a $-45^{o}$. Esto puede suceder en el conjunto $S$ sólo para el unico punto en
el que se intersecan L y S. Al referirnos a las curvas de nivel de $f$ se indica que este punto $(-\frac{1}{1},\frac{1}{2})$ es un mínimo relativo de $f|_s$ (Pero no de $f$).

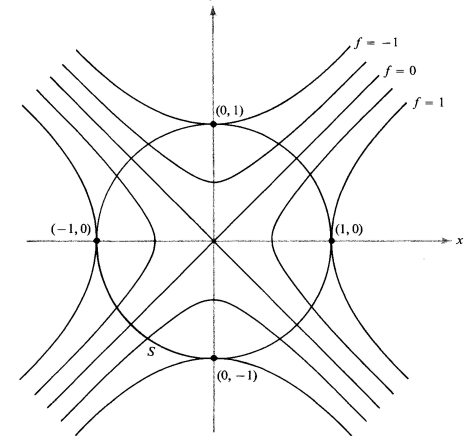
$\textbf{Ejemplo.}$ Sea $f:\mathbb{R}^2\rightarrow \mathbb{R}$ dada asi $f(x,y)=x^2-y^2$ y sea $S$ el círculo de radio 1 alrededor del origen. Hallar los extremos de $f|_s$.

$Solución.$ El conjunto $S$ es la curva de nivel para $g$ con valor $t$. Donde $g:\mathbb{R}^2\rightarrow \mathbb{R}$, $(x,y) \rightarrow x^2+y^2$. La condición de que $\nabla f=\lambda \nabla g$ en $x_0$, es decir que $\nabla f$ y $\nabla g$ son pararlelos en $x_0$, es la misma que las curvas de nivel sean tangentes en $x_0$. Asi los puntos extremos de $f |_s$ son $(0,\pm 1)$ y $(\pm1,0)$. Evaluando $f$ hallamos que $(0,\pm 1)$ son mínimos y $(\pm1,0)$ son máximos. Usando Multiplicadores de
lagrange $\nabla f(x,y)=(2x,2y)$ y $\nabla g(x,y)=(2x,2y)$\ $\therefore$ \quad $(2x,-2y)=\lambda(2x,2y)$ cuya solución es $(0,\pm 1)$, $(\pm1,0)$.

$\textbf{Ejemplo.}$ Maximizar la función $f(x,y,z)=x+z$ sujeta a la restricción $x^2+y^2+z^2=1$

$Solución.$ Buscamos $\lambda$ y $(x,y,z)$ tales que $1=2x\lambda$, $0=2y\lambda$ y $1=2z\lambda$ $x^2+y^2+z^2=1$ la solución es $(\frac{1}{\sqrt{2}},0,\frac{1} {\sqrt{2}})$, $(-\frac{1}{\sqrt{2}},0,-\frac{1}{\sqrt{2}})$ comprobando los valores de $f$ en estos puntos podemos ver que el primer punto produce el máximo de $f$ y el segundo el mínimo.

$\textbf{Ejemplo.}$ Hallar los puntos extremos de $f(x,y,z)=x+y+z$ sujeto a las dos condiciones $x^2+y^2=2$ y $x+z=1$

$Solución.$ Aquí hay dos restricciones $g_1=(x,y,z)=x^2+y^2-2=0$ $g_2(x,y,z)=x+z-1=0$ asi, debemos encontrar $x,y,z,\lambda_1$ y $\lambda_2$ tales que $$\nabla f(x,y,z)=\lambda_1 \nabla g (x,y,z)+ \lambda_2 \nabla g_2(x,y,z)$$
$$g_1(x,y,z)=0 \quad y \quad g_2(x,y,z)=0$$
Calculando gradientes e igualando componentes, obtenemos

$\begin{eqnarray}
1=\lambda_1\cdot 2x+\lambda_2\cdot 1\\
1=\lambda_1 2y+\lambda_2\cdot 0\\
1=\lambda_1\cdot 0 + \lambda_2\cdot 1\\
x^2+y^2=2\\
x+z=1
\end{eqnarray}$

De (3) $\lambda_2=1$ y asi $2x\lambda_1=0$, $2y\lambda_1=1$.

Como la segunda implica $\lambda_1\neq 0$ $x=0$. Asi $y=\pm\sqrt{2}$ y $z=1$. Entonces los extremos deseados son $(0,\pm\sqrt{2},1)$.

Por inspección $(0,\sqrt{2},1)$ da un máximo relativo y $(0,-\sqrt{2},1)$ un mínimo relativo.

La condición $x+z=1$ implica que $z$ tambien está acotada. Se deduce que el conjunto de restricciones $S$ es cerrada y acotada,

Por lo tanto $f$ tiene un máximo y un mínimo en $S$ que se deben alcanzar en $(0,\sqrt{2},1)$ y $(0,-\sqrt{2},1)$ respectivamente.