4. Relaciones morfométricas y alometría: funciones potenciales
4.1 Alometría: tamaño y forma en biología
La alometría es el estudio de cómo los cambios en el tamaño de un organismo afecta a sus características, lo que puede involucrar transformaciones morfológicas, así como modificaciones ecológicas, fisiológicas y conductuales. Es muy importante para comprender las relaciones entre distintas características físicas, como la altura y el peso, en organismos animales y vegetales. La alometría también es importante en la investigación ecológica y evolutiva, ayudando a entender los patrones de crecimiento y adaptación de las especies.
Modelo matemático
La fórmula básica para representar una relación alométrica es:
$y = ax^b$
donde, y es la variable dependiente (por ejemplo, el peso de un órgano), x es la variable independiente (por ejemplo, el tamaño del individuo), a es una constante que depende del sistema biológico que estamos estudiando, b es el exponente alométrico.
Por ejemplo, supongamos que estamos midiendo el volumen x y la masa y de diferentes especies de mamíferos. Sea la ecuación
$y = 0.1 \cdot x^{3/4}$,
podemos interpretar que, aunque el volumen crece más rápidamente que la masa, la masa no aumenta de manera proporcional al volumen debido a la eficiencia metabólica y estructural de los animales más grandes. Es decir, en esta ecuación, el exponente $\frac{3}{4}$ es el que marca la relación entre la masa y y el volumen x del individuo. Si analizamos esto, vemos que la relación no es directamente proporcional porque el exponente no es 1. Si fuera y = ax, esto significaría que la masa aumenta de manera proporcional al volumen; en otras palabras, si el volumen se duplicara, la masa también se duplicaría. Pero en este caso, como el exponente es menor que 1, la masa aumenta a un ritmo más lento que el volumen. Es decir, si el volumen se duplica, la masa no lo hará en la misma proporción.
Además es importante cuestionarse ¿por qué la masa no aumenta proporcionalmente al volumen? Esto se puede deber a:
• Eficiencia metabólica
Reiss plantea que los organismos más grandes pueden tener una mayor proporción de tejido menos activo metabólicamente, por lo que, aunque en términos absolutos un animal grande tenga una tasa metabólica mayor que uno pequeño, su tasa metabólica por unidad de masa es menor (Reiss, p. 7). Esto se debe a que, aunque los animales grandes tienen más células y órganos, el aumento en tamaño no implica que todas las funciones metabólicas (como la digestión, la circulación o el transporte de oxígeno) aumenten al mismo ritmo. La masa no aumenta tan rápidamente como el volumen.
• Estructura
A medida que un animal aumenta su tamaño durante su desarrollo, su estructura también cambia. Las proporciones de las diferentes partes de su cuerpo se ajustan para soportar el aumento de tamaño, pero no todos los componentes crecen al mismo ritmo. Por ejemplo, en un individuo los huesos deben ser cada vez más gruesos para sostener el aumento de masa, pero no crecen proporcionalmente al volumen total del cuerpo. Esta adaptación estructural también explica por qué la masa no crece de manera proporcional al volumen en lo que respecta a los huesos.
Thompson plantea que existe un límite definido para la posible magnitud de un animal que vive bajo la acción directa de la gravedad. El elefante, por ejemplo, al observar las dimensiones de los huesos de sus extremidades se pueden ver signos de una tendencia al grosor desproporcionado. Menciona que “a medida que el tamaño de un animal aumenta, sus miembros tienden a volverse más gruesos y cortos, y todo el esqueleto se vuelve más voluminoso y pesado. Los huesos constituyen alrededor del 8% del cuerpo de un ratón, 13 o 14% de un ganso o perro, y 17 o 18% del cuerpo de un hombre.» (Thompson, p. 26-28).
Es importante señalar que estos porcentajes varían dependiendo del medio en el que el animal se desarrolle. Por ejemplo, animales terrestres y marinos presentan diferencias en su composición ósea debido a las distintas condiciones ambientales. En el caso de los patos y las gallinas, las diferencias en sus alas y en cómo crecen son clave para sus capacidades de vuelo. Los patos, por estar adaptados para volar, tienen alas más grandes en relación con su cuerpo, mientras que las gallinas, al no ser voladoras, tienen alas más pequeñas y no están adaptadas para el vuelo, lo que refleja cómo su crecimiento y estructura están influenciados por el entorno en el que viven.
Ahora supongamos que tenemos una planta cuyo tamaño en altura x se relaciona con su tasa de crecimiento medida como el aumento en su peso y. Si esta relación estuviera definida por:
$y = 0.5 \cdot x^{1.2}$,
podríamos predecir que, a medida que la planta crece, su tasa de crecimiento también aumenta, pero a un ritmo ligeramente mayor que su aumento en tamaño. Al tener un exponente mayor que 1, su tasa de crecimiento y aumentará más rápidamente que el tamaño de la planta x. Es decir, cuando la planta crece más en altura, no solo aumentará en tamaño, sino que la cantidad de recursos metabólicos (como nutrientes, agua, luz solar) que puede captar y procesar la planta, también crece a un ritmo mayor. Esto podría deberse a que las plantas más grandes tienen una mayor capacidad para realizar fotosíntesis y, por lo tanto, pueden aumentar su masa a una tasa más alta que su simple crecimiento en tamaño.
Ejemplo
Sea un elefante adulto de 3.3 metros de altura y 6 000 kilogramos de masa. Supongamos que queremos modelar la relación entre el peso de la masa (y) y la altura (x) de dicho elefante utilizando un modelo alométrico de la forma: $y = a \cdot x^b$, donde:
- y es el peso del elefante en kilogramos,
- x es la altura del elefante en metros,
- a es una constante específica para esta relación,
- b es el exponente alométrico, que refleja cómo varía el peso con respecto a la altura.
Nota importante: el valor del exponente b para especies grandes, como los elefantes, generalmente se obtiene a través de estudios empíricos. En muchos mamíferos grandes, el exponente alométrico b suele estar en el rango de 2.5 a 3. Este valor se ha observado en estudios alométricos realizados por biólogos que modelan la relación entre el tamaño y el peso de diferentes especies de mamíferos. Por ejemplo, según Reiss en sus estudios de alometría en elefantes africanos (Loxodonta africana) encontró que el exponente b se encuentra cerca de 2.7 (Reiss, p. 47).
Usamos los valores de los datos conocidos para encontrar la constante a en la ecuación alométrica. Sabemos que: x = 3.3 m (altura), y = 6000 kg (peso), y suponemos que b = 2.7.
Sustituyendo en la ecuación: $y = a \cdot x^b \Rightarrow 6000 = a \cdot (3.3)^{2.7}$.
Resolvemos para a: $a = \frac{6000}{38.3} \approx 156.5$.
De manera que la ecuación que describe la relación buscada es: $y = 156.5 \cdot x^{2.7}$.
Podemos decir que este modelo muestra que el peso del elefante africano aumenta a un ritmo mucho más rápido que la altura. Esto es consistente con la idea de que los animales más grandes necesitan estructuras corporales más robustas para sostener su tamaño. La constante a refleja la escala de la relación para esta especie en particular, y el exponente b = 2.7 indica que, por cada unidad de aumento en la altura, el peso aumenta de manera más que proporcional.
Ejemplo
Sea una planta de maíz de 2.5 metros de altura y 5 kilogramos de masa. Supongamos que queremos modelar la relación entre el peso de la masa (y) y la altura de la planta (x), utilizando un modelo alométrico de la forma: $y = a \cdot x^b$, donde:
- y es el peso de la planta en kilogramos,
- x es la altura de la planta en metros,
- a es una constante específica para esta relación,
- b es el exponente alométrico.
Nota importante: para las plantas, el valor del exponente b generalmente se encuentra en el rango de 1.1 a 1.3. Este valor depende de cómo el crecimiento de la biomasa se ve influenciado por factores como la capacidad de la planta para realizar fotosíntesis, la disponibilidad de recursos y las condiciones ambientales. En estudios de alometría para el maíz, se ha observado que el exponente b está alrededor de 1.2.
Usamos los valores de los datos conocidos para encontrar la constante a. Sabemos que: x = 2.5 m (altura), y = 5 kg (peso), y suponemos que b = 1.2.
Sustituyendo en la ecuación: $y = a \cdot x^b \Rightarrow 5 = a \cdot (2.5)^{1.2}$
Ahora resolvemos para a: $a = \frac{5}{3.16} \approx 1.58$.
Por lo que la ecuación que describe la relación que buscamos es: $y = 1.58 \cdot x^{1.2}$.
Podemos observar que este modelo muestra que, a medida que la planta de maíz crece en altura, su peso aumenta a un ritmo mayor. Esto tiene sentido, ya que las plantas más altas tienen más capacidad para captar luz solar, agua y nutrientes, lo que les permite incrementar su masa de manera más rápida a medida que crecen.
Ejercicio
Sea una planta de agave de 1.8 metros de altura y 25 kilogramos de masa. Modela la relación entre el peso de la masa (y) y la altura de la planta (x), utilizando un modelo alométrico de la forma: $y = a \cdot x^b$. Considera un exponente alométrico b = 1.2.
4.2 Propiedades de las potencias y los logaritmos
Las potencias y los logaritmos son funciones matemáticas y herramientas importantes para estudios biológicos, especialmente en el análisis de relaciones exponenciales entre variables. Estas relaciones pueden aparecer en modelos de crecimiento, distribución de recursos, y escalas de tamaño en organismos vivos. A través de las propiedades de las potencias y la transformación logarítmica, podemos simplificar la resolución de ecuaciones complejas, además de visualizar relaciones no lineales de manera más clara.
Potencias
Las potencias son funciones matemáticas de la forma $x^b$, donde b es un exponente. Estas funciones forman una familia de curvas, cuya forma cambia dependiendo del valor de b. A continuación se puede observar gráficamente esta familia de curvas para algunos valores de b:
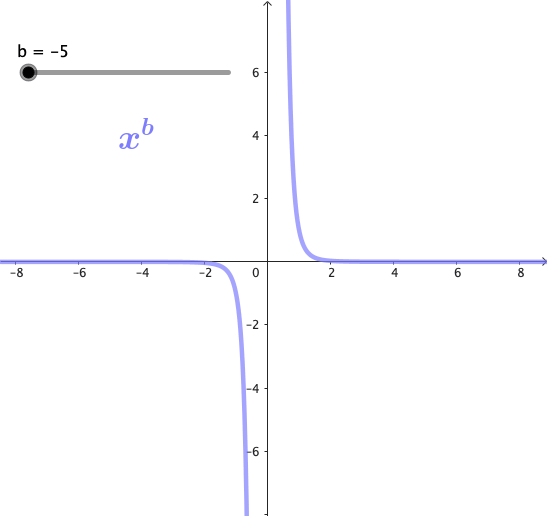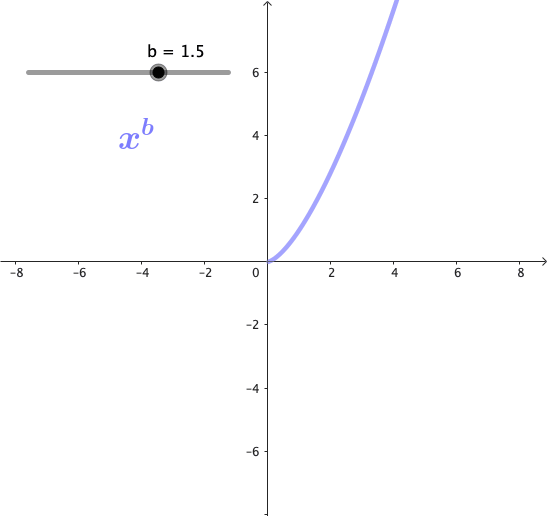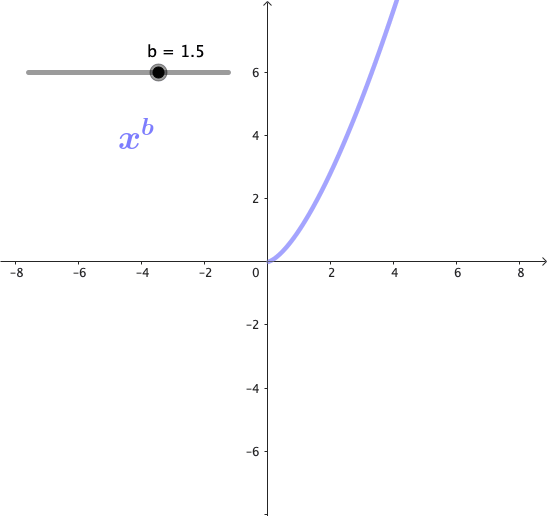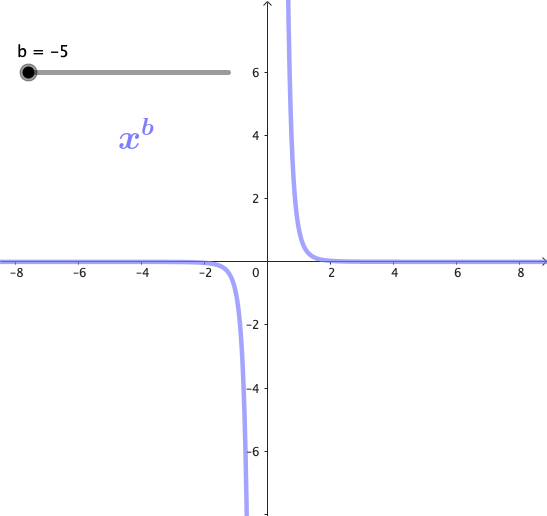
Propiedades de las potencias
- $x^a \cdot x^b = x^{a+b}$
Ejemplo: $x^3 \cdot x^4 = x^{3+4} = x^7$ - $\left(x^a\right)^b = x^{a \cdot b}$
Ejemplo: $\left(x^3\right)^2 = x^{3 \cdot 2} = x^6$ - $\frac{x^a}{x^b} = x^{a-b}$
Ejemplo: $\frac{x^7}{x^3} = x^{7-3} = x^4$
Estas propiedades nos permiten simplificar expresiones algebraicas complejas y que resulte más sencillo operar con ellas. Al transformar las potencias, podemos estudiar cómo las variables se afectan entre sí.
Ejercicios
a. $x^2 \cdot x^5$
b. $x^6 \cdot x^3$
c. $\left(x^2\right)^4$
d. $\left(x^5\right)^3$
e. $\frac{x^8}{x^2}$
f. $\frac{x^9}{x^4}$
Logaritmos
Los logaritmos son el proceso inverso de la potenciación. Mientras que la potenciación nos permite elevar una base a un exponente, el logaritmo nos permite encontrar el exponente al que debemos elevar una base para obtener un determinado valor. Por ejemplo, el logaritmo en base 10 de 1000 es 3, porque $10^3 = 1000$.
La propiedad básica de los logaritmos es la siguiente:
$\log_b(xy) = \log_b(x) + \log_b(y)$
Esto quiere decir que el logaritmo de un producto es la suma de los logaritmos de los factores.
A continuación se puede observar gráficamente las familias de curvas de las funciones inversas para algunos valores de a:
Propiedades de los logaritmos
- Producto: $\log_b(x \cdot y) = \log_b(x) + \log_b(y)$
Ejemplo: Si x = 2 e y = 8, calculamos $\log_2(2 \cdot 8)$: $\log_2(16) = \log_2(2) + \log_2(8)$
Sabemos que $\log_2(16) = 4$,$\log_2(2) = 1$ y $\log_2(8) = 3$, por lo tanto: 4 = 1 + 3. - Cociente: $\log_b\left(\frac{x}{y}\right) = \log_b(x) – \log_b(y)$
Ejemplo: Si x = 8 e y = 2, calculamos $\log_2\left(\frac{8}{2}\right)$: $\log_2(4) = \log_2(8) – \log_2(2)$
Sabemos que $\log_2(4) = 2$, $\log_2(8) = 3$ y $\log_2(2) = 1$, por lo tanto: 2 = 3 – 1. - Potencia: $\log_b(x^n) = n \cdot \log_b(x)$
Ejemplo: Si x = 2 y n = 3, calculamos $\log_2(2^3)$: $\log_2(8) = 3 \cdot \log_2(2)$
Sabemos que $\log_2(8) = 3$ y $\log_2(2) = 1$, por lo tanto: $3 = 3 \cdot 1$. - Cambio de Base: $\log_b(x) = \frac{\log_c(x)}{\log_c(b)}$
Ejemplo: Si x = 8, b = 2 y c = 10, calculamos $\log_2(8)$ utilizando la base 10: $\log_2(8) = \frac{\log_{10}(8)}{\log_{10}(2)}$
Sabemos que $\log_{10}(8) \approx 0.903$ y $\log_{10}(2) \approx 0.301$, por lo tanto: $\log_2(8) = \frac{0.903}{0.301} \approx 3$ - Logaritmo de 1: $\log_b(1) = 0 \quad \text{para cualquier base} \, b > 0$
Ejemplo: Si b = 5, entonces: $\log_5(1) = 0$
Transformación logarítmica
Si tenemos una ecuación de una función exponencial de la forma $y = ax^b$, podemos aplicar logaritmos de base 10 o natural para obtener una relación lineal:
$y = ax^b \Rightarrow \log(y) = \log(a) + b\log(x).$
De esta forma, los datos pueden ser graficados en un sistema de coordenadas log-log, y la pendiente de la recta resultante será igual al valor de b.
Ejemplo
Dado un conjunto de datos con las variables de masa corporal y y altura x a lo largo del desarrollo de una especie, al aplicar logaritmos a ambos valores, se podrían graficar estos valores y ver si los datos siguen una línea recta. Si la relación es alométrica, la pendiente de esa línea corresponderá al exponente b.
- Sea el siguiente conjunto de datos sobre la masa corporal (kg) y altura (cm) de un ciervo a lo largo de su desarrollo: (50, 3.5), (80, 12), (90, 25), (100, 40), (110, 60), (120, 80).
El primer paso es aplicar el logaritmo en base 10 a ambos valores:
| x (altura en cm) | y (masa en kg) | log(x) | log(y) |
| 50 | 3.5 | 1.698970004 | 0.5440680444 |
| 80 | 12 | 1.903089987 | 1.079181246 |
| 90 | 25 | 1.954242509 | 1.397940009 |
| 100 | 40 | 2 | 1.602059991 |
| 110 | 60 | 2.041392685 | 1.77815125 |
| 120 | 80 | 2.079181246 | 1.903089987 |
Al graficar los dos conjuntos de datos, obtenemos las gráficas:
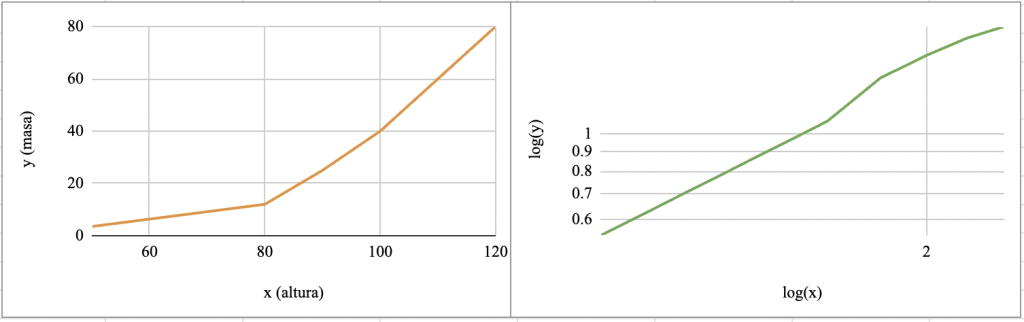
Ejemplo
Para calcular la pendiente de la recta logarítmica obtenida (continuando con la información del ejemplo anterior) usamos la fórmula de la pendiente $b = \frac{(y_2 – y_1)}{(x_2 – x_1)}$, donde $(x_1, y_1)$ y $(x_2, y_2)$ son dos puntos transformados.
Tomamos un par de puntos (1.698970004, 0.5440680444) y (1.903089987, 1.079181246):
$b = \frac{(1.079181246 – 0.5440680444)}{(1.903089987 – 1.698970004)}$
$= \frac{0.5351132016}{0.204119983} \approx 2.62156205$
Ejercicio
Dada la ecuación $y = 0.5 \cdot x^{2.1}$, realiza su transformación logarítmica.
Ejercicio
Dado el siguiente conjunto de puntos (x, y): (1, 2), (2, 8), (4, 32), (8, 128), (16, 512), esboza la curva que representan. Luego realiza su transformación logarítmica y encuentra el lugar geométrico que describen los nuevos datos.
Ejercicio
En un estudio sobre la relación entre la masa corporal y la altura de una especie de mamífero terrestre, se ha observado que estas dos variables siguen una relación alométrica. Se te proporcionan los siguientes datos para una muestra de 6 individuos:
| Individuo | x (altura en cm) | y (masa en kg) |
| 1 | 33 | 2.5 |
| 2 | 51.5 | 7 |
| 3 | 58 | 12.5 |
| 4 | 69 | 18 |
| 5 | 83 | 24.5 |
| 6 | 92 | 32 |
- Grafica los puntos y encuentra la curva alométrica.
- Transforma los valores de altura x y masa y de cada individuo aplicando logaritmos de base 10 (puedes usar una hoja de cálculo para tener resultados más precisos).
- Grafica los puntos transformados en un sistema de coordenadas log-log.
- Calcula la pendiente de la recta que pasa por los puntos transformados, que representará el valor del exponente b en la ecuación alométrica (puedes usar la fórmula de la pendiente $b = \frac{(y_2 – y_1)}{(x_2 – x_1)}$.
4.3 Transformación de datos y ajuste de curvas alométricas
Transformación de datos
Como se mencionó anteriormente, cuando los datos de un experimento no siguen una relación lineal directa, podemos transformarlos para hacer que sigan una tendencia más fácil de analizar. En biología, esto ocurre comúnmente cuando estamos trabajando con relaciones exponenciales.
Para transformar los datos, se puede aplicar el logaritmo de cada uno de los valores. Este proceso es útil cuando tenemos datos que siguen una ley del tipo $y = ax^b$, ya que al aplicar el logaritmo, transformamos la relación en una forma lineal:
$\log(y) = \log(a) + b \log(x)$
Esta transformación convierte la relación no lineal en una recta, la cual podemos analizar utilizando métodos estadísticos.
Ajuste de curvas alométricas
El ajuste de curvas implica encontrar el valor de a y b que mejor describen la relación entre las variables y y x. Para hacer esto, se puede usar el método de mínimos cuadrados que es una técnica utilizada para encontrar la recta que mejor se ajusta a un conjunto de datos minimizando la suma de las diferencias cuadradas entre los valores observados y los valores predichos por la recta. La recta se describe con la ecuación $Y=mX+c$, donde m es la pendiente de la recta y c es la intersección o el valor de Y cuando X = 0.
La intención del método es encontrar la recta que minimice la suma de las diferencias cuadradas entre los valores observados (los puntos reales en el gráfico) y los valores predichos por la recta. No podemos esperar que todos los puntos encajen en la recta, sin embargo, se busca encontrar la mejor aproximación posible.
Para encontrar esta recta debemos considerar la siguiente fórmula para encontrar la pendiente m:
$m = \frac{\sum_{i=1}^n x_i \cdot (y_i – \bar{y})}{\sum_{i=1}^n x_i \cdot (x_i – \bar{x})},$
donde:
- $x_i$ y $y_i$ son los valores individuales de los datos transformados de x e y,
- $\bar{x}$ y $\bar{y}$ son las medias de $\log(x)$ y $\log(y)$, respectivamente.
La fórmula propuesta es una expresión estándar derivada de los principios del ajuste de curvas mediante el método de mínimos cuadrados, y nos da el valor de la pendiente de la recta que mejor aproxima los datos transformados.
Una vez que hemos calculado la pendiente m, podemos calcular la intersección c, que es el valor de $\log(y)$ cuando $\log(x) = 0$. Para calcular c, utilizamos la siguiente fórmula:
$c = \frac{\sum y_i – m \cdot \sum x_i}{n},$
donde:
- $\sum y_i$ es la suma de los valores de $\log(y)$,
- $\sum x_i$ es la suma de los valores de$\log(x)$,
- m es la pendiente que hemos calculado previamente,
- n es el número total de puntos de datos.
Ésta fórmula proviene de la ecuación general de la recta $Y = mX + c$, evaluada en los puntos medios de los valores de X e Y. Esta fórmula garantiza que la recta pase por el promedio de los puntos transformados.
Ejemplo
Supongamos que se tiene un conjunto de datos de peso y y tamaño x de diferentes individuos que cumple con una relación alométrica. Los datos obtenidos son:
(x, y) = (2, 10), (4, 16), (8, 40), (16, 100)
Queremos encontrar la ecuación $y = a x^b$ utilizando el método de mínimos cuadrados.
• Paso 1: Transformación logarítmica de los datos
Como estamos trabajando con una relación alométrica del tipo $y = ax^b$, aplicamos logaritmos en base 10 a ambos valores de x e y:
$\log(x) = \{0.3010, 0.6021, 0.9031, 1.2041\}$ y $\log(y) = \{1, 1.2041, 1.6021, 2\}.$
Luego, los puntos transformados son:
$(\log(x), \log(y)) = (0.3010, 1), (0.6021, 1.2041), (0.9031, 1.6021), (1.2041, 2)$
• Paso 2: Ajuste de la recta usando mínimos cuadrados
Ahora que tenemos los puntos transformados, ajustamos una recta $Y = mX + c$, donde $Y = \log(y) y X = \log(x)$. Consideramos la fórmula para calcular la pendiente m:
$m = \frac{\sum_{i=1}^n x_i \cdot (y_i – \bar{y})}{\sum_{i=1}^n x_i \cdot (x_i – \bar{x})}$
Primero, calculamos los promedios de $\log(x)$ y $\log(y)$:
$\bar{x} = \frac{0.3010 + 0.6021 + 0.9031 + 1.2041}{4} = 0.7526$
$\bar{y} = \frac{1 + 1.2041 + 1.6021 + 2}{4} = 1.4513$
Luego, calculamos las sumas necesarias:
$\sum x_i \cdot (y_i – \bar{y}) = (0.3010)(1 – 1.4513) + (0.6021)(1.2041 – 1.4513) + (0.9031)(1.6021 – 1.4513) + (1.2041)(2 – 1.4513)$
$= (0.3010)(-0.4513) + (0.6021)(-0.2472) + (0.9031)(0.1508) + (1.2041)(0.5487)$
$= -0.1359 + (-0.1486) + 0.1362 + 0.6603 = 0.5120$
$\sum x_i \cdot (x_i – \bar{x}) = (0.3010)(0.3010 – 0.7526) + (0.6021)(0.6021 – 0.7526) + (0.9031)(0.9031 – 0.7526) + (1.2041)(1.2041 – 0.7526)$
$= (0.3010)(-0.4516) + (0.6021)(-0.1505) + (0.9031)(0.1505) + (1.2041)(0.4515)$
$= -0.1359 + (-0.0906) + 0.1362 + 0.5436 = 0.4533$
Ahora, sustituimos los valores en la fórmula para la pendiente m:
$m = \frac{0.5120}{0.4533} \approx 1.13$
• Paso 3: Cálculo de la intersección c
Para calcular la intersección c consideramos la fórmula:
$c = \frac{\sum y_i – m \cdot \sum x_i}{n}$
Primero, calculamos las sumas:
$\sum y_i = 1 + 1.2041 + 1.6021 + 2 = 5.8062$
$\sum x_i = 0.3010 + 0.6021 + 0.9031 + 1.2041 = 3.0103$
Sustituimos los valores en la fórmula de c:
$c = \frac{5.8062 – (1.13)(3.0103)}{4} = \frac{5.8062 – 3.4022}{4} = \frac{2.4040}{4} = 0.6010$
• Paso 3: Definición de la ecuación de la recta
La ecuación de la recta transformada es:
$\log(y) = 1.13 \log(x) + 0.6010$
Para obtener la ecuación original $y = a \cdot x^b$ a partir de los datos obtenidos, sabemos que b = m = 1.13 y $\log(a) = c = 0.6010$.
Por lo tanto, $a = 10^{0.6010} \approx 4.0$.
Así que la ecuación alométrica que buscamos es:
$y = 4 \cdot x^{1.13}$.
Ejercicio
Supongamos que estamos estudiando la relación entre la altura x (cm) y el peso y (kg) de pumas macho en una zona montañosa de México. Los datos obtenidos para cuatro individuos son los siguientes:
$(x, y) = (220, 60), (230, 62), (225, 64), (210, 58)$
Encuentra la ecuación $y = a \cdot x^b$ que mejor describa la relación alométrica utilizando el método de mínimos cuadrados.
4.4 Otras funciones potenciales en biología: el metabolismo y las leyes de Kleiber y Rubner
Ley de Kleiber
La ley de Kleiber establece que la tasa metabólica M (generalmente en calorías o kilocalorías por día) de los organismos es proporcional a su masa corporal (en kilogramos) W elevada a la ¾. Esta ley se puede expresar como:
$M = a \cdot W^{3/4}$,
donde a es una constante de proporcionalidad que se determina experimentalmente y varía entre diferentes grupos de organismos (mamíferos, aves, reptiles, etc.). Esta constante refleja la eficiencia metabólica del organismo y la forma específica en que su cuerpo utiliza la energía en función con su masa. Por ejemplo, en mamíferos, la constante a suele tener un valor cercano a 70, aunque puede ajustarse para cada especie dependiendo de su metabolismo y características fisiológicas.
Concepto clave: Aunque los animales más grandes tienen una mayor tasa metabólica, esta no es proporcional al tamaño de su masa debido a factores como la eficiencia del metabolismo y la distribución de la energía.
Ejemplo
Supongamos que un animal tiene una masa de 500 kg y una constante a = 70, entonces usando la ley de Kleiber, podemos calcular su tasa metabólica:
$M = 70 \cdot 500^{3/4} \approx 70 \cdot 105.7371 \approx 7401.59$kcal/día.
Este cálculo nos indica que el animal consume aproximadamente 7401.59 kcal por día, que es su tasa metabólica según la ley de Kleiber.
Ley de Rubner
La ley de Rubner establece que la tasa metabólica M de un organismo es proporcional a su superficie corporal A, con la fórmula:
$M = k \cdot A^{2/3}$,
donde k es una constante que se determina experimentalmente y depende de la forma del animal y de cómo se distribuye su masa en relación con su superficie. Cada especie tiene un valor único de k basado en su morfología y distribución corporal; los animales más grandes tienen un valor más pequeño de k, mientras que los animales más pequeños, tendrán un valor de k más grande, ya que su forma está más adaptada a perder calor rápidamente. Los valores de k usualmente oscilan entre 60 y 80 para mamíferos en general.
Concepto clave: En organismos pequeños, la superficie corporal es crucial para determinar la tasa metabólica debido a su papel en el intercambio de calor y energía con el ambiente. A medida que los animales son más pequeños, su área superficial en relación con el volumen es mayor, lo que favorece la pérdida de calor.
Ejemplo
Vamos a comparar cómo cada ley describe la tasa metabólica de dos animales de tamaños muy diferentes: un ratón y un elefante.
Ley de Kleiber
La ley de Kleiber describe cómo la tasa metabólica está relacionada con la masa corporal.
Para ello, utilizamos la fórmula $M = a \cdot W^{3/4}$ con los siguientes datos respectivamente:
- Masa del ratón: $W_{\text{ratón}} = 0.03 \, \text{kg}$
- Masa del elefante: $W_{\text{elefante}} = 5000 \, \text{kg}$
- $a_{\text{ratón}} = 70$
- $a_{\text{elefante}} = 80$
Calculamos sus tasas metabólicas
Ratón: $M_{\text{ratón}} = 70 \cdot 0.03^{3/4} \approx 70 \cdot 0.0721 \approx 5.05 \, \text{kcal/día}$
Elefante: $M_{\text{elefante}} = 80 \cdot 5000^{3/4} \approx 80 \cdot 594.6 \approx 47568.28 \, \text{kcal/día}$
Ley de Rubner
La ley de Rubner, por otro lado, describe la tasa metabólica en función de la superficie corporal A. Usamos la fórmula:
$M = k \cdot A^{2/3}$
supongamos $k_{\text{ratón}} = 70$ y $k_{\text{elefante}} = 60$.
Para usar esta ley, necesitamos calcular el área superficial de cada animal. Aproximamos la superficie corporal A de un organismo utilizando la fórmula:
$A = k \cdot W^{2/3}$
supongamos $k_{\text{ratón}} = 10$ y $k_{\text{elefante}} = 5$.
Calculamos el área superficial de cada animal y a continuación sus tasas metabólicas
Ratón:
$A_{\text{ratón}} = 10 \cdot 0.03^{2/3} \approx 10 \cdot 0.098 \approx 0.98 \, \text{m}^2$
$\Rightarrow M_{\text{ratón}} = b \cdot 0.97^{2/3} \approx 70 \cdot 0.98 \approx 68.59 \, \text{kcal/día}$
Elefante:
$A_{\text{elefante}} = 5 \cdot 5000^{2/3} \approx 5 \cdot 292.40 \approx 1462 \, \text{m}^2$
$\Rightarrow M_{\text{elefante}} = b \cdot 1462^{2/3} \approx 60 \cdot 1462^{2/3} \approx 60 \cdot 128.81 \approx 7728.87 \, \text{kcal/día}$
Observaciones:
• La ley de Kleiber se basa en la relación entre la masa corporal de un organismo y su tasa metabólica, y muestra que los organismos más grandes tienen una tasa metabólica mayor, pero no proporcional a su masa. Los resultados muestran que el elefante, con una masa mucho mayor, tiene una tasa metabólica considerablemente mayor (aproximadamente 47568 kcal/día) en comparación con el ratón (aproximadamente 5.05 kcal/día). Esto es consistente con la hipótesis de que los animales grandes requieren más energía, pero la relación no es directamente proporcional a su masa.
• La ley de Rubner se enfoca en la superficie corporal, lo que es un factor importante en el intercambio de calor y la eficiencia metabólica de los animales, sobre todo en los más pequeños, que tienden a tener una tasa metabólica relativamente más alta en relación con su masa, ya que tienen más superficie en proporción a su volumen. En este caso, el ratón tiene una tasa metabólica más alta (aproximadamente 68.59 kcal/día) que el elefante (aproximadamente 7728.87 kcal/día), lo que refleja que los animales pequeños tienen una tasa metabólica más alta debido a la mayor superficie corporal relativa.
Podemos concluir que:
La ley de Kleiber es más adecuada para animales grandes, donde la masa corporal es el factor dominante que determina el metabolismo; y la ley de Rubner es más adecuada para animales pequeños, donde la superficie corporal juega un papel crucial en la tasa metabólica debido a la mayor tasa de pérdida de calor y eficiencia energética.
Referencias bibliográficas
Thompson, D’ A. W. 1992 On growth and form: the complete revised edition. Dover, Nueva York.
Reiss, Michael J. 1989. The Allometry of Growth and Reproduction. Cambridge University Press, Cambridge.
Evaluación
1. Elige la respuesta correcta
a. La alometría describe únicamente cómo cambia el peso de un organismo a medida que crece.
A) Verdadero
B) Falso
b. ¿Cuál de las siguientes ecuaciones representa una relación alométrica?
A) $y = a + bx$
B) $y = a \cdot x^b$
C) $y = \log(x + a)$
D) $y = a \cdot \exp(bx)$
c. ¿Qué representa el exponente b en una ecuación alométrica?
A) Una constante relacionada con la unidad de medida
B) La tasa metabólica
C) El tipo de relación entre tamaño y forma
D) La pendiente de una recta horizontal
d. ¿Cuál es la ventaja de aplicar logaritmos a una relación $y = ax^b$?
A) Hacerla no diferenciable
B) Eliminar la constante a
C) Convertirla en una relación lineal
D) Aumentar la tasa de crecimiento
e. Supón que una especie vegetal tiene una relación alométrica dada por $y = 2 \cdot x^{1.5}$, donde y es la masa en kg y x la altura en metros.
• ¿Cuál es la masa cuando la planta mide 2 metros?
• ¿Qué tipo de crecimiento indica el exponente 1.5?
f. Considera la ecuación alométrica $y = 0.8 \cdot x^{2.1}$. Realiza su transformación logarítmica y escribe la forma lineal resultante.
g. A partir de los siguientes datos:
| x (cm) | y (kg) |
| 30 | 3 |
| 60 | 10 |
• Aplica logaritmo base 10 a los valores.
• Calcula la pendiente que define el valor del exponente alométrico b.
2. Resuelve
a. Se investigan dos especies vegetales: una de hojas grandes (palma) y otra de hojas pequeñas o menos extensas (agave). Ambas tienen masas similares, pero distintas relaciones entre su área superficial y volumen. Se quiere analizar cómo varía su crecimiento metabólico usando un modelo de tipo alométrico y observar qué tipo de planta se ajusta mejor a qué tipo de modelo.
Datos (altura en m, masa en kg):
• Palma: (1.5, 30), (2, 60), (2.5, 95), (3, 140)
• Agave: (0.5, 8), (0.8, 20), (1, 30), (1.3, 45)
i. Ajusta un modelo alométrico $y = a \cdot x^b$ a cada conjunto de datos.
ii. Realiza la transformación logarítmica para ambos y calcula el valor del exponente b.
iii. Representa gráficamente las relaciones en escala log-log.
iv. Compara la forma de crecimiento de ambas plantas e interpreta el papel que podría jugar la morfología de sus hojas.
v. Redacta una conclusión: ¿cuál crece más rápidamente en masa en relación a su tamaño? ¿Por qué podría ser útil este tipo de análisis en agronomía o ecología?
b. Se han registrado datos de masa corporal W en kilogramos para un ratón y un elefante en distintas etapas de su desarrollo. Utiliza la Ley de Kleiber y la Ley de Rubner para calcular la tasa metabólica M de ambos organismos.
Datos:
• Para el ratón (masa en kg): 0.01, 0.02, 0.04, 0.08
• Para el elefante (masa en kg): 500, 1000, 3000, 6000
• Constantes:
○ $a_{\text{ratón}} = 70$, $a_{\text{elefante}} = 80$
○ $k_{\text{ratón}} = 75$, $k_{\text{elefante}} = 65$
○ $c_{\text{ratón}} = 10$, $c_{\text{elefante}} = 5$
i. Calcula la tasa metabólica de cada organismo con ambas leyes para cada masa.
ii. Realiza dos gráficas por separado para cada organismo (una con la ley de Kleiber y otra con la de Rubner).
iii. Compara los patrones de crecimiento en las gráficas.
iv. Redacta una conclusión sobre cuál ley describe mejor la tasa metabólica de cada organismo y por qué.
