Introducción
En este apartado se abordará el primer método para valuar proyectos de inversión, es conocido como Tasa Interna de Retorno, y tiene sus bases en el modelo de interés compuesto, que ya se han venido utilizando anteriormente.
Método de la Tasa Interna de Retorno (TIR), para valuar proyectos de inversión
La Tasa Interna de Retorno (TIR), es la tasa de interés, con la que los flujos de valor presente se hace cero, en otras palabras, es la tasa que hace que los ingresos y los egresos sean iguales.
Regularmente la ecuación de valor que se utiliza, describe los flujos de un proyecto de inversión y es de grado mayor que 2, motivo por el cual la TIR, es calculada por medio de un proceso iterativo (de repetición).
En dicha ecuación, se reflejan las bases del cálculo de la tasa interna de retorno, y de la valuación de proyectos de inversión:
$$M=K(1+i)^t$$
de este modelo surge la siguiente ecuación:
$$0=M-K(1+i)^t$$
ó bien,
$$0=M-Kv^t$$
En ambos modelos, la tasa de interés que hace 0 la diferencia entre la cantidad invertida menos la recibida, es lo que se conocerá como tasa de rendimiento de la inversión.
En los proyectos de inversión, en los que no se conoce la cantidad que se va a invertir, la tasa de interés, el plazo, los flujos de la misma, los proyectos de inversión de obras o negocios (tales como obras, adquisición de maquinaria, compra de patentes, modernización tecnológica, etc.), dichos flujos deben ser calculados específicamente para el proyecto del que se esté valuando, una vez obtenidos, calcular el valor presente y su respectiva tasa de interés que vuelve cero la ecuación.
El procedimiento para hacer la valuación es el siguiente:
- Calcular los ingresos y egresos, que se estén considerados para obtener y para invertir del proyecto, para cada uno de los periodos que dure el proyecto.
- Obtener el valor presente de los flujos netos (ingresos – egresos) a una cierta tasa.
- Determinar la tasa interna de retorno (y/o algunos otros indicadores como la TIR ajustada), el periodo de recuperación, la rentabilidad contable media, y el índice de rentabilidad.
Algunas reglas para su uso
- El cálculo de los ingresos así como de los egresos, debe de hacerse basándose en estudios de mercado (precios y cantidades), costo de las construcciones y maquinaria, duración de las máquinas, su tiempo de vida, tiempos de instalación, de mantenimiento, además; de considerar el capital de trabajo que se necesitara para operar.
- Determinar la periodicidad de los «cortes» que sea acorde a la duración del proyecto.
- Hacer uso de una tasa adecuada para determinar el valor presente neto.
- Ser cuidadoso al interpretar el manejo de las TIR’s no calculables o de varios valores.
- Tener cuidado con proyectos que consideren inversiones posteriores, las cuales arrojen flujos negativos.
- La aceptación o rechazo de la TIR dependerá de su tamaño. En general si la TIR es mayor que la tasa de referencia que se esté usando (como por ejemplo, tasa CETE o alguna otra), el proyecto se acepta, si es menor, entonces el proyecto se rechaza.
- El inversionista puede solicitar, para algún proyecto cualquiera, que se calcule una prima de riesgo por que involucra al proyecto mismo. Dicha tasa se convierte en una «sobretasa» que se suma a la tasa de referencia. Su tamaño dependerá del tamaño del riesgo, a mayor riesgo, mayor tasa.
- La tasa de rendimiento que espera tener el inversionista se compara contra la que arroja la valuación del proyecto.
- Hay casos en los que la TIR no puede ser calculada, o puede tener varios valores. En dichas situaciones el analista deberá revisar los flujos, y en caso de ser necesario, partir el proyecto en varias etapas, para valuar por separado cada uno, obtener las TIR’s y luego de eso, poder tomar la decisión que corresponda.
Si la tasa de rendimiento esperara es > que la TIR, entonces se rechaza
Si la tasa de rendimiento esperada es < que la TIR, entonces se acepta.
Es importante señalar que la TIR se calcula por iteraciones tomando como base los flujos netos a los precios del periodo que corresponde.
Las tasas de cada iteración arrojan un determinado VPN, la TIR es la tasa a la que el VPN es igual a CERO. La TIR debe de tener una periodicidad de una tamaño que cada de los periodos.
Ejercicios resueltos
Ejercicio. A continuación, se quiere calcular la TIR del proyecto de inversión en una planta armadora de equipo electrónico, con los siguientes registros:
Solución
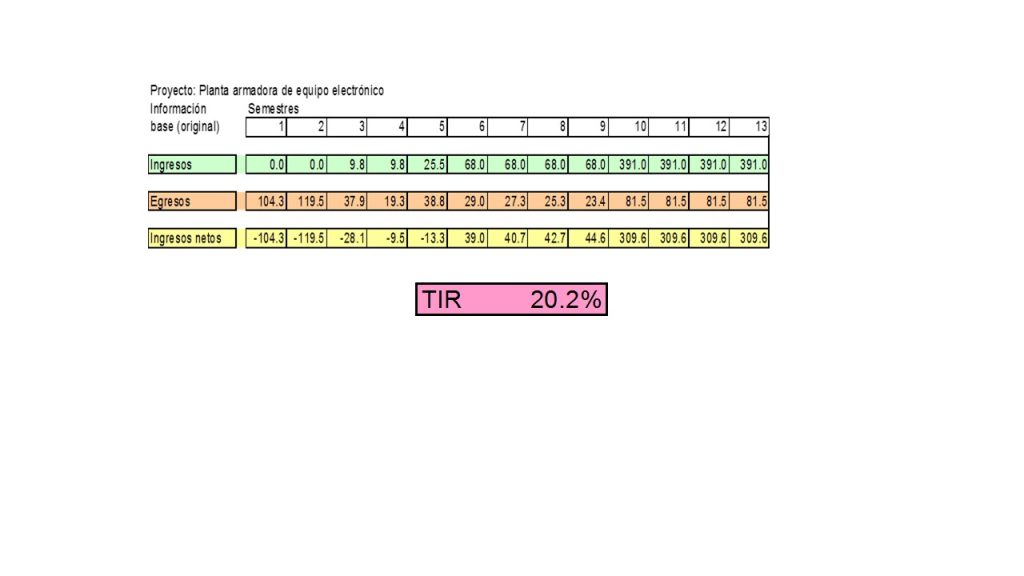
En este caso la TIR es del 20.2%, lo cual nos dice que es casi el triple de la tasa actual promedio de pagarés bancarios liquidables al vencimiento para 360 días, lo que la vuelve atractiva para el proyecto. Sin embargo, la tasa de rendimiento que esperaba tener el inversionista fue de 35%, lo cual probablemente, nos dice que el inversionista rechazaría éste proyecto ya que va a esperar uno que le ofrezca una tasa mejor.
Ejercicio. Se tiene un proyecto de inversión, para el cual se tuvo el registro que muestra los siguientes flujos de efectivo:
- Inversión inicial de 5000 pesos
- El proyecto en cuestión ofrece tener un ingreso de 3000 pesos en el primer año, 3500 en el segundo año.
Se desea conocer la TIR, y determinar si el proyecto es viable
Solución
Para saber la respuesta se hace lo siguiente:
$$Ingresos Netos=-5000+\frac{3000}{(1+i)}+\frac{2500}{(1+i)^2}+\frac{1500}{(1+i)^3}$$
Queremos conocer el valor de $i$
$$-5000(1+i)^2+3000(1+i)+3500=0$$
$$-5000(1+2i+i^2)+3000+3000i+3500=0$$
$$(-5000-10000i-5000i^2)+3000i+6500=0$$
$$7000i-5000i^2+1500=0$$
$$-5000i^2+7000i=-1500$$
$$5000i^2-7000i=1500$$
$$i=1.58$$
EL valor de la TIR es del 1.58%
Más adelante…
Se continuaran abordando, diferentes formas de combinar cada una de las herramientas que se van adquiriendo en cada apartado, con la finalidad de poder evidenciar su aplicación, así como sus respectivas reglas para utilizarlas.
Ir a Matemáticas Financieras
Entrada anterior
Entrada siguiente
