Introducción

Los diversos tipos de anualidades que se han estado analizando, nos dotan de herramienta muy importante, y que como se ha estado observando, se pueden utilizar de diferentes maneras, dependiendo del contexto y las necesidades de las partes involucradas en una operación financiera. Para cada una de ellas, se ha visto que se puede hacer una construcción de una tabla de amortización que describa el comportamiento de los pagos, así como la forma en que va disminuyendo.

Concepto y descripción

Para cualesquiera de las anualidades, ya se ha dado la forma en que se construye su respectiva tabla de amortización, ya que es análogo a como se ha venido trabajando, solo hay que continuar obedeciendo las reglas que fueron utilizadas anteriormente para su construcción, tomando en cuenta las condiciones bajo las cuales se esté trabajando, tales como, las tasas de interés, la periodicidad que dure la operación, el cálculo de las tasas de equivalencia (cuando así lo requieran), etc.

A continuación, se procederá a construir algunos tipos de tablas de amortización, que por su naturaleza, es necesario hacer cierto hincapié.

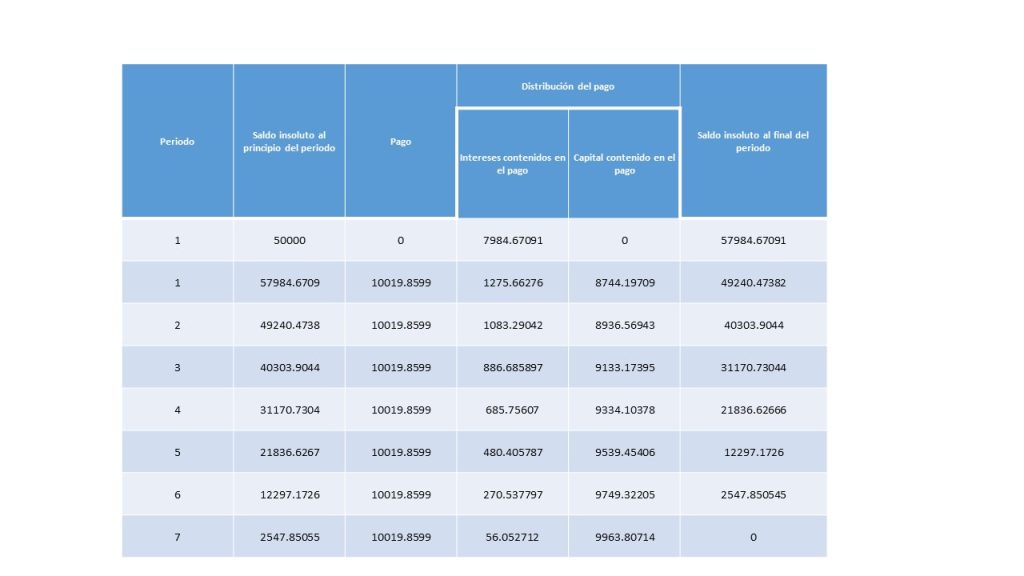
Tabla de amortización para créditos diferidos.

Este tipo de amortización, corresponde al comportamiento en el que el tipo de crédito genera intereses durante el periodo de diferimiento, los cuales se acumulan al capital insoluto.

Para su construcción, en la primera celda se establecerá el periodo de diferimiento y se hará el registro de los intereses devengados durante dicho periodo. Mientras que la celda que corresponde a la columna de saldo insoluto al final del periodo de gracia, será igual a la suma del crédito original más la suma de los intereses que se acaban de calcular.

Para realizar la construcción del segundo renglón, el cual mostrará el primer periodo de pago, se obtendrá de forma análoga a como se obtiene el de una anualidad vencida. Los demás renglones seguirán el mismo proceso de construcción.

Para evidenciar dicha construcción, se desarrollará el siguiente ejemplo:

La compañía necesita dar mantenimiento a su parque vehicular, para hacerlo solicita un crédito que asciende a la cantidad de \$50 mil pesos y quiere pagarlo, de forma bimestral, con una tasa de interés del 14% bimestral. Comenzará a realizar los pagos, después de medio año, a través de 6 pagos bimestrales de forma vencida. Se desea saber el monto de cada pago y su tabla de amortización.

Para resolverlo, se utiliza la siguiente ecuación de valor:

$$S=X\prescript{}{n}{\mathbf{A}}_{i}=X\left(\frac{1-v_i^n}{i}\right)$$

$$X=\frac{S}{\prescript{}{n}{\mathbf{A}}_{i}v_{i}^n}.$$

Sustituyendo los valores:

$$50,000=\prescript{}{6/6}{\mathbf{A}}_{0.025}$$

$$X=\frac{50,000}{\prescript{}{6}{\mathbf{A}}_{0.025}v_{0.025}^6}$$

$$X=\frac{50,000}{(5.5081254)(0.9059506)}=10,019.85985.$$

Los intereses devengados durante los 6 meses que corresponden al periodo de gracia o periodo de diferimiento, se obtienen:

$$I=50,000(1+.025)^6-50,000=7984.670911.$$

De esta forma la tabla de amortización queda de la siguiente manera:

Ejercicios resueltos

Ejercicio. Una empresa necesita \$95 mil pesos, para abrir una nueva sucursal de venta de ropa, por tal capital le cobran una tasa de interés del 18% pagadera semestralmente, dicho préstamo acuerda comenzar a pagarlo después de 6 meses, y planea pagarlo en 6 pagos semestrales. Calcular el valor de cada pago.

Ejercicio. Calcular la tabla de amortización del ejercicio anterior.

Más adelante…

Se continuará estudiando este tipo de material, aún falta por analizar las tablas de amortización para créditos con pagos crecientes, así como los decrecientes, tienen ambas similitudes al operarlas de forma semejante a como fueron trabajadas sus respectivas anualidades. También se abordarán algunos ejemplos de situaciones en las cuales se pueden aplicar.

• Ir a Matemáticas Financieras
• Entrada anterior
• Entrada siguiente