Introducción

En este material, se ha estado abordando los modelos de interés compuesto, su evolución con las anualidades, las tasas de interés, sus tipos, y combinación de cada una de ellas dependiendo de la forma en que se realicen los pagos, y dependiendo también del tipo de tasa de interés con la que se decida trabajar.

Concepto y descripción

En este apartado, se desarrollará el tipo de amortización con pajos fijos, así como tasas de interés fijas. Las manejaremos con el nombre de amortización de créditos con pagos fijos al capital, y en este rubro encajan las tablas de amortización con anualidades ordinarias vencidas.

Su desarrollo justo, tiene que ver con las herramientas vistas en el tema que lleva el mismo nombre, la cual, suele representar la forma más utilizada para hacer el pago de una deuda, por lo que resulta necesario hacer algunos recordatorios:

La forma general de la ecuación de valor que se va a estar utilizando será:

$$S=X\prescript{}{n}{\mathbf{A}}_i$$

donde para estos fines, $S$ representa el monto de la deuda y que equivale al saldo insoluto al inicio de la operación, mientras que la variable $X$, representa la cantidad que será pagada en cada periodo.

Las filas y columnas serán calculadas de forma análoga al tema anterior.

Para el primer periodo, el saldo insoluto será calculado con la siguiente expresión:

$$\prescript{}{n}{\mathbf{A}}_i=\frac{1-v^n}{i}$$

luego los intereses contenidos en el pago se van a multiplicar por la tasa de interés, esto es:

$$\frac{1-v^n}{i}(i)=1-v^n$$

ahora el capital contenido en el pago se calcula al restar la celda con el nombre de intereses contenidos en el pago, y esto se traduce en:

$$1-(1-v^n)=1-1+v^n=v^n.$$

Por último, la celda con el nombre de saldo insoluto al final del periodo se obtiene al efectuar la resta del saldo al principio del periodo, el capital contenido en el pago, lo cual es:

$$\left(\frac{1-v^n}{i}\right)-v^n.$$

De la expresión que se acaba de obtener, nos fijamos en el factor común, para tener la siguiente ecuación:

$$\frac{1-v^n-iv^n}{i}$$

luego factorizamos a $v^{n-1}$, y la ecuación se transforma en:

$$\frac{1-v^{n-1}(v+iv)}{i}.$$

Recordando que $v=\frac{1}{1+i}$, la expresión que se obtiene es:

$$\frac{1-v^{n-1}\left(\frac{1}{1+i}+\frac{i}{1+i}\right)}{i}$$

como $(1+i)$ es el común denominador, entonces:

$$\frac{1-v^{n-1}\left(\frac{1+i}{1+i}\right)}{i}$$

la cantidad que se tiene expresada entre paréntesis es igual a uno, entonces la ecuación queda:

$$\frac{1-v^{n-1}}{i}.$$

Recordando que, $\prescript{}{n}{\mathbf{A}}_i=\frac{1-v^n}{i}$ y haciendo mención que todos los cálculos que hasta el momento se han estado realizando, son con un capital de un peso, además se está manejando una anualidad vencida de $n-1$ pagos, entonces se tiene:

$$\prescript{}{n-1}{\mathbf{A}}_i=\frac{1-v^{n-1}}{i}.$$

Este resultado tiene sentido, toda vez que al final del primer periodo se hizo el primero de los $n$ pagos de la anualidad, lo cual implica que en ése momento aun faltan por realizar $n-1$ pagos, los cuales en valor presente en ése periodo son: $\prescript{}{n}{\mathbf{A}}_i$, expresión que representa la cantidad que se obtiene como saldo insoluto al final del periodo.

A continuación, se procederá a construir la tabla de amortización de una anualidad vencida ordinaria de $n$ pagos, con un capital de un peso.

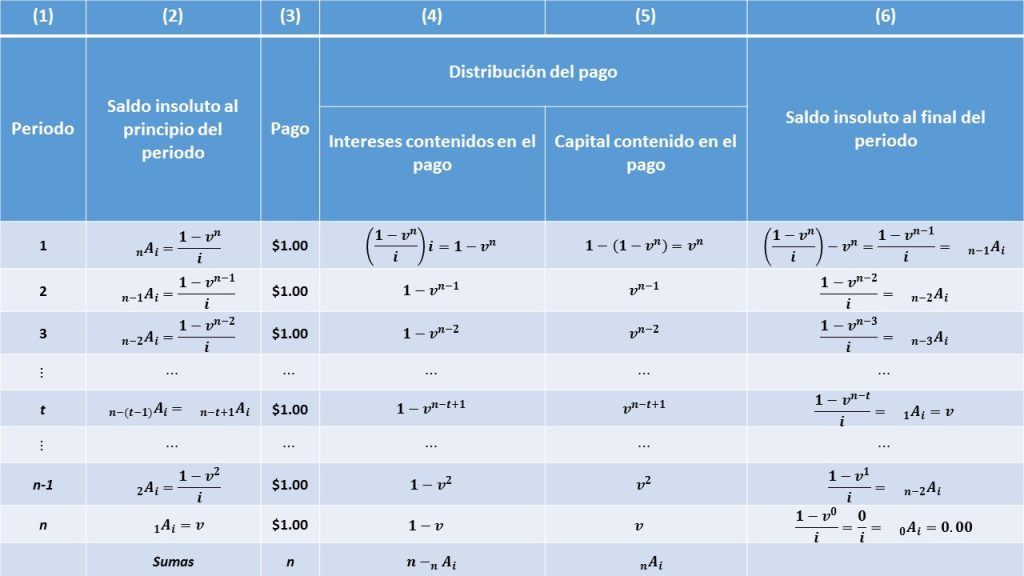
Es importante hacer mención que, en la tabla que se acaba de presentar, la tasa de interés permanece constante, por dicha razón es que no aparece el subíndice $i$ en las expresiones de las $v^t$. Además, el renglón expresado con la letra, $t$ permite hacer el cálculo de cualquiera de las filas, sin tener que calcular toda la tabla, esto nos sirve cuando se da el caso de que el deudor, quiera conocer cuál es el saldo insoluto de su préstamo en cualquier momento, siempre y cuando esté comprendido en el periodo de la vigencia de la operación. Esto también sirve si se desea liquidar en ese momento la totalidad de la deuda o quiera hacer alguna reestructuración de la misma.

Ahora generalizando la tabla anterior, y sustituyendo el valor de un peso de capital, por la cantidad $X$, se tiene lo siguiente:

Para conocer el valor de $X$, que es la cantidad que determina el pago en la ecuación de valor, se utiliza la expresión:

$$S=X\prescript{}{n}{\mathbf{A}}_i$$

despejando a $X$ se tiene:

$$X=\frac{S}{\prescript{}{n}{\mathbf{A}}_i}$$

y la tabla queda modificada de la siguiente manera:

Ejercicios resueltos

Ejercicio. El señor Juan desea adquirir una pantalla, para ello solicitó un préstamo por \$30 mil pesos, el cual desea pagar a 24 mensualidades, a una tasa de interés del 15% efectivo mensual, durante toda la duración del crédito. Si al cabo de un año desea liquidar la deuda, ¿Cuál es la cantidad que deberá pagar?

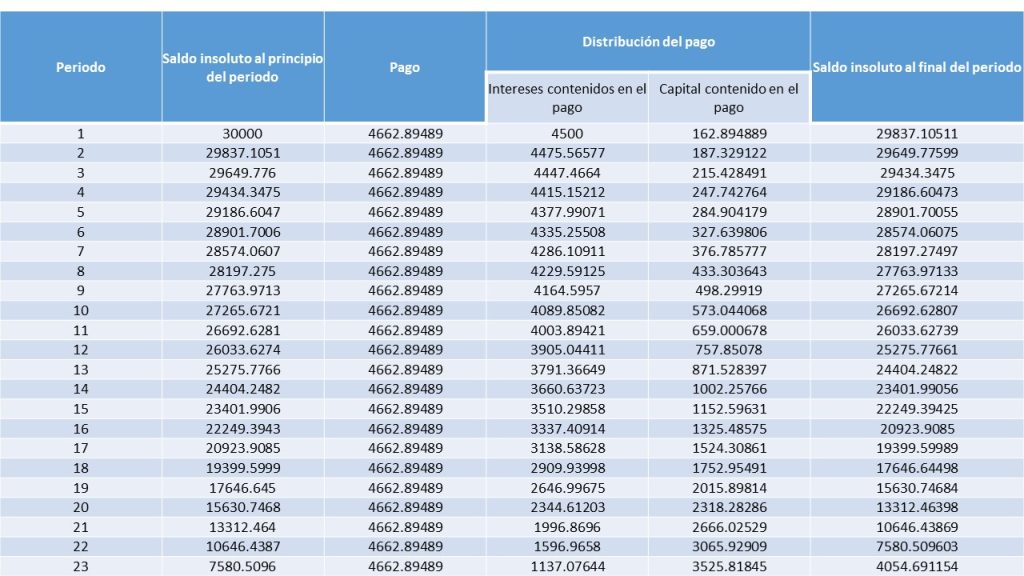
Ejercicio. Calcula la tabla de amortización del ejercicio anterior y corrobora el resultado.

Más adelante…

Hay ocasiones en los que el mercado financiero, por alguna razón puede sugerir hacer cambios en ésta, dependiendo de muchos otros factores en los que se encuentre la economía, un ejemplo de esto es cuando se decide trabajar con una tasa de interés variable que dependa de alguna tasa de referencia, lo cual afecta directamente la forma en que se vaya a pagar.

• Ir a Matemáticas Financieras
• Ir a Entrada Anterior
• Ir a Entrada Siguiente