Dada una función de dos variables que está
definida sobre el rectángulo cerrado
$$R=[a,b]\times[c,d]={(x,y)\in\mathbb{R}^{2}\mid a\leq x\leq b,
c\leq y \leq d}$$ suponiendo que $f(x,y)\geq 0$. La gráfica de f es
una superfície con ecuación $z=f(x,y)$. Sea S el sólido que esta
encima de R y debajo de la gráfica de f, es decir
$$S={(x,y,z)\in \mathbb{R}^{3}\mid 0\leq z\leq f(x,y),(x,y)\in R}$$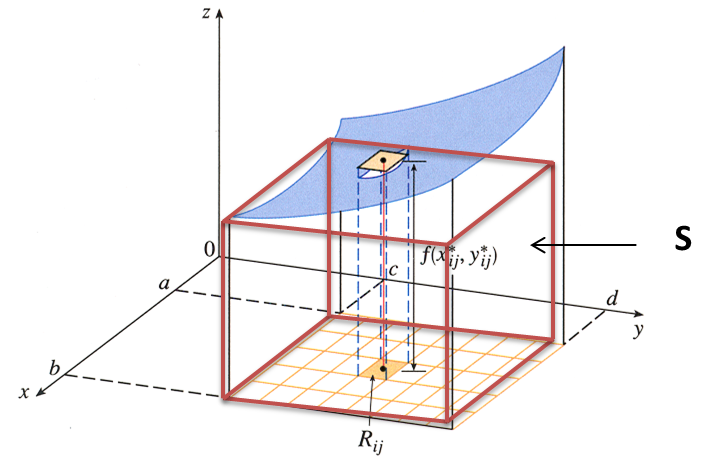

Si cortamos nuestra región por un plano paralelo al plano YZ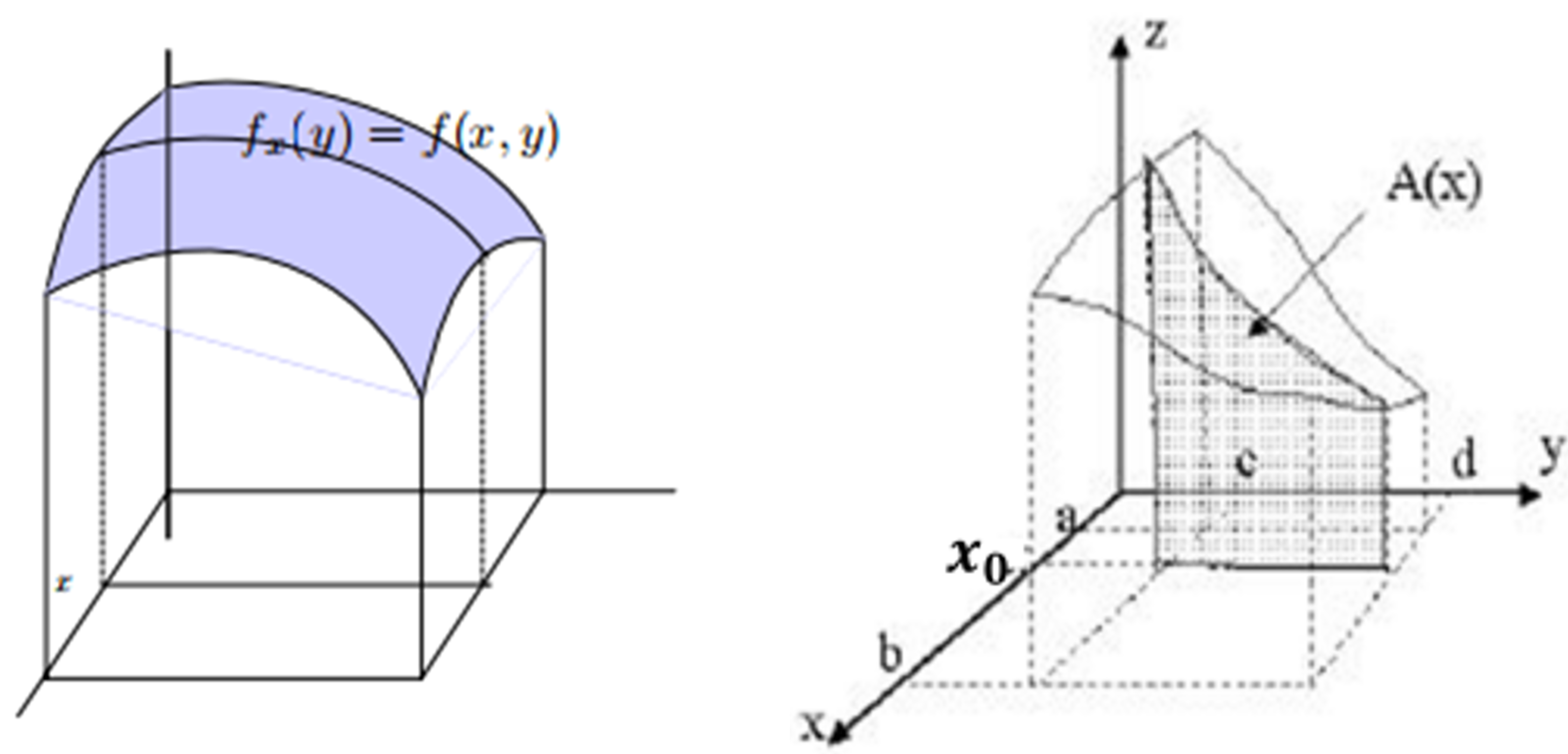

a la altura del punto $x_{0}\in [a, b]$ del eje X, la figura que se obtiene es la misma que obtenemos al considerar aquella que está por debajo de la gráfica de la función $f_{x_{0}}: [c, d] \rightarrow\mathbb{R}$ definida como
$$f_{x_{0}}(y)=f(x_{0},y)$$
de esta forma, el área de la figura correspondiente al corte realizado a la altura $x_{0}$ que podemos denotar $\alpha(x_{0})$ coincide con ser
$$\alpha(x_{0})=\int_{c}^{d}f(x_{0})(y)dy=\int_{c}^{d}f(x_{0},y)dy$$
También podemos hacer cortes con planos paralelos al plano XZ; así si cortamos a la altura del punto $y_{0}\in [c, d]$ del eje Y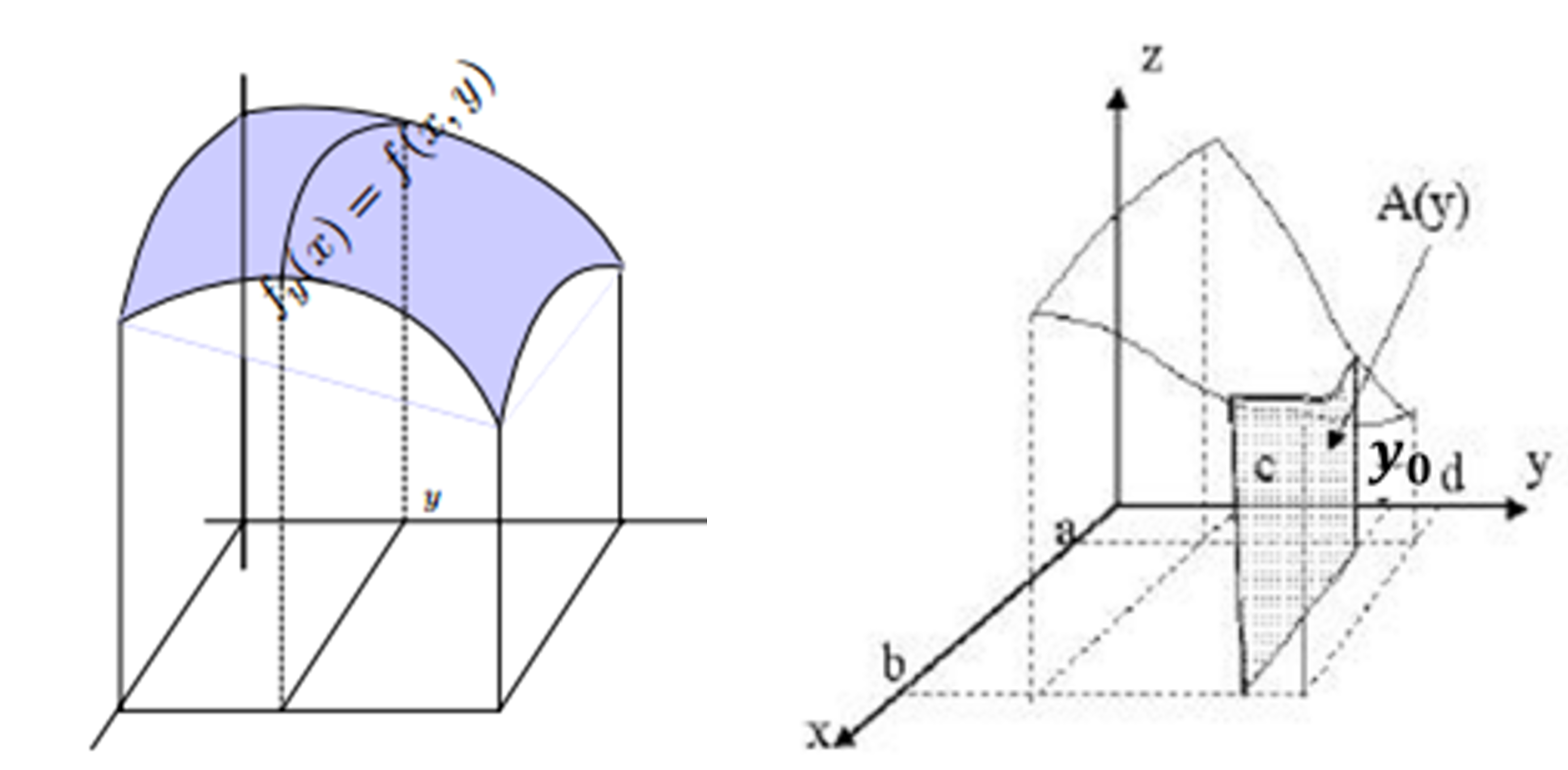

se obtiene es la misma que obtenemos al considerar aquella que está por debajo de la gráfica de la función $f_{y_{0}}: [a, b] \rightarrow\mathbb{R}$ definida como
$$f_{y_{0}}(x)=f(x,y_{0})$$
de esta forma, el área de la figura correspondiente al corte realizado a la altura $y_{0}$ que podemos denotar $\beta(y_{0})$ coincide con ser
$$\beta(y_{0})=\int_{a}^{b}f_{y_{0}}(x)dx=\int_{a}^{b}f(x,y_{0})dx$$
En este caso $\beta$ es una función definida sobre el intervalo $[c, d]$.
Por tanto el volumen del sólido entre la superfície y el rectángulo R estará dado por
$$\int_{R}\alpha(x)dx=\int_{a}^{b}\left(\int_{c}^{d}f(x,y)dy\right)dx$$
o por
$$\int_{R}\beta(x)dy=\int_{c}^{d}\left(\int_{a}^{b}f(x,y)dx\right)dy$$
$\boxed{\Large{\textcolor{red}{Teorema~de~Fubini}}}$
El teorema de Fubini nos va a dar una técnica para el cálculo de integrales de funciones de varias variables mediante el cálculo de varias integrales de funciones de una variable. A partir de ahí se podrán utilizar todas las técnicas conocidas del Análisis de una variable para el cálculo de integrales mediante cálculo de primitivas y el teorema fundamental del cálculo (Regla de Barrow): cambios de variables, integración por partes, etc.
$\boxed{\textcolor{red}{Teorema:}}$
Sean $[a,b]\subset\mathbb{R}$ y $[c,d]\subset \mathbb{R}$ dos intervalos tal que, $R= [a,b]\times [c,d]$, y $f: R\subset\mathbb{R}\rightarrow\mathbb{R}^{2}$ una función integrable.

Para cada $\hat{y}$ fijo en $[c,d]$ definimos $f_{\hat{y}}:[t_{i-1},t_{i}]\subset\mathbb{R}\rightarrow\mathbb{R}$ como
$$f_{\hat{y}}=f(x,\hat{y})$$
y definimos
$$\phi(\hat{y})=\underline{\int_{t_{i-1}}^{t_{i}}}f_{\hat{y}}(x)dx$$
$$\psi(\hat{y})=\overline{\int_{t_{i-1}}^{t_{i}}}f_{\hat{y}}(x)dx$$
Si f es integrable sobre R entonces $\phi, \psi$ son integrables sobre $[c,d]$ y además
$$\int_{R}f=\int_{c}^{d}\phi(y)dy=\int_{c}^{d}\psi(y)dy$$
$\boxed{\textcolor{red}{Demostración:}}$
Observemos en primer lugar que una partición de $R = [a,b]\times [c,d]$ esta formada por una partición de $[a,b]$ y otra de $[c,d]$. Sea $$P_{1}\in P_{[a,b]}=\{a=t_{0},t_{1},…,t_{n}=b\}$$ y sea
$$P_{2}\in P_{[c,d]}=\{c=t_{0},t_{1},…,t_{m}=d\}$$
$$P=P_{1}\times P_{2}\in P_{R} $$
Y cualquier rectángulo de la partición P tiene área $|t_{i}-t_{i-1}|\cdot|t_{j}-t_{j-1}|$,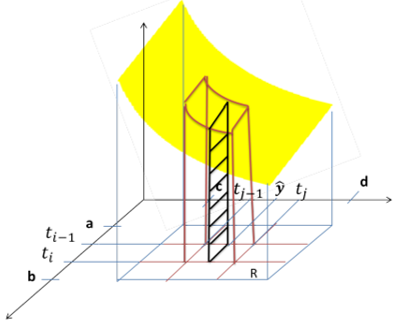

Para cada $\hat{y}$ fijo en $[c,d]$ definimos
\begin{align*}
m_{j}(\phi)&=\inf\{\phi(\hat{y})~\Big{|}~\hat{y}\in[t_{j-1},t_{j}]\}\\
M_{j}(\phi)&=\sup\{\phi(\hat{y})~\Big{|}~\hat{y}\in[t_{j-1},t_{j}]\}\\
m_{j}(\psi)&=\inf\{\psi(\hat{y})~\Big{|}~\hat{y}\in[t_{j-1},t_{j}]\}\\
M_{j}(\psi)&=\sup\{\psi(\hat{y})~\Big{|}~\hat{y}\in[t_{j-1},t_{j}]\}\\
m_{i}(f_{\hat{y}})&=\inf\{f_{\hat{y}}(x)~\Big{|}~x\in[t_{i-1},t_{i}]\}\\
M_{i}(f_{\hat{y}})&=\sup\{f_{\hat{y}}(x)~\Big{|}~x\in[t_{i-1},t_{i}]\}\\
m_{ij}(f)&=\inf\{f(x,y)~\Big{|}~(x,y)\in R_{ij}\}\\
M_{ij}(f)&=\sup\{f(x,y)~\Big{|}~(x,y)\in R_{ij}\}
\end{align*}
De lo anterior tenemos que se cumple
$$m_{ij}(f)\leq m_{i}(f_{\hat{y}})\leq M_{i}(f_{\hat{y}})\leq M_{ij}(f)$$
Multiplicando por $(t_{i} − t_{i−1}) > 0$ se tiene
$$m_{ij}(f)(t_{i} − t_{i−1}) \leq m_{i}(f_{\hat{y}})(t_{i} − t_{i−1}) \leq M_{i}(f_{\hat{y}})(t_{i} − t_{i−1}) \leq M_{ij}(f)(t_{i} − t_{i−1}) $$
Sumando sobre i
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1}) \leq \sum_{i=1}^{n}m_{i}(f_{\hat{y}})(t_{i} − t_{i−1}) \leq \sum_{i=1}^{n}M_{i}(f_{\hat{y}})(t_{i} − t_{i−1}) \leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1}) $$
se tiene entonces
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1}) \leq \underline{S}(f_{\hat{y}},P) \leq \overline{S}(f_{\hat{y}},P)\leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1}) $$
Sabemos que
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1}) \leq \underline{S}(f_{\hat{y}},P)\leq \phi(\hat{y})\leq \psi(\hat{y})\leq \overline{S}(f_{\hat{y}},P)\leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1}) $$
Esto pasa para toda $\hat{y}\in[c,d]$ esto prueba que los extremos de estas desigualdades son cota inferior y superior (respectivamente) tanto de $\psi$ como de $\phi$ en el subrectángulo $R_{ij}$ y por lo tanto tendremos que
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})\leq m_{j}(\phi)\leq M_{j}(\phi)\leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})$$
y también
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})\leq m_{j}(\psi)\leq M_{j}(\psi)\leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})$$
Multiplicando por $(t_{j} − t_{j−1}) > 0$ se tiene
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) \leq m_{j}(\phi)(t_{j} − t_{j−1}) \leq M_{j}(\phi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) $$
y también
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) \leq m_{j}(\psi)(t_{j} − t_{j−1}) \leq M_{j}(\psi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) $$
Sumando sobre j
$$\sum_{i=1}^{m}\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}m_{j}(\phi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}M_{j}(\phi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}\sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) $$
y también
$$\sum_{i=1}^{m}\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}m_{j}(\psi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}M_{j}(\psi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}\sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) $$
se tiene entonces
$$\underline{S}(f,P)\leq \underline{S}(\phi,P)\leq \overline{S}(\phi,P)\leq \overline{S}(f,P)$$
y también
$$\underline{S}(f,P)\leq \underline{S}(\psi,P)\leq \overline{S}(\psi,P)\leq \overline{S}(f,P)$$
como f es integrable sobre R, entonces las funciones $\psi$ y $\phi$ son integrables sobre $[c, d]$ y además
$$\int_{R}f=\int_{c}^{d}\phi(y)dy=\int_{c}^{d}\psi(y)dy$$
Es decir
$$\int_{R}=\int_{c}^{d}\left(\int_{a}^{b}f(x,y)dx\right)dy$$
siguiendo estos pasos pero considerando ahora un $x_{o}$ fijo en [a, b] y haciendo variar la y se tendría
$$\int_{R}=\int_{a}^{b}\left(\int_{c}^{d}f(x,y)dy\right)dx$$
Es decir
$$\int_{R}=\int_{a}^{b}\left(\int_{c}^{d}f(x,y)dy\right)dx=\int_{c}^{d}\left(\int_{a}^{b}f(x,y)dx\right)dy\blacksquare$$
$\boxed{\textcolor{green}{Ejemplo}}$
Si $R=[-1,1]\times \left[0,\frac{\pi}{2}\right]$, calcular
$$\int_{R}(x\sin(y)-ye^{x})dxdy$$
$\boxed{\textcolor{green}{Solución}}$
Integrando primero respecto a x tenemos
$$\int_{0}^{\frac{\pi}{2}}\left(\int_{-1}^{1}(x\sin(y)-ye^{x})dx\right)dy=\int_{0}^{\frac{\pi}{2}}\left(\frac{x^{2}}{2}\sin(y)-ye^{x}\Big{|}_{-1}^{1}\right)dy=\int_{0}^{\frac{\pi}{2}}\left(-ey+\frac{y}{e}\right)dy$$
$$=\left(\frac{1}{e}-e\right)\int_{0}^{\frac{\pi}{2}}y~dy=\left(\frac{1}{e}-e\right)\frac{\pi^{2}}{8}$$
en el otro orden de integración
$$\int_{-1}^{1}\left(\int_{0}^{\frac{\pi}{2}}(x\sin(y)-ye^{x})dy\right)dx=\int_{-1}^{1}\left(x\cos(y)-\frac{y^{2}e^{x}}{2}\Big{|}_{0}^{\frac{\pi}{2}}\right)dx=\int_{-1}^{1}\left(-\frac{\pi^{}e^{x}}{8}+x\right)dx$$
$$=\left(\frac{1}{e}-e\right)\frac{\pi^{2}}{8}$$

Se dice que una función $\color{blue}{f(x)}$ es continua en un punto $\color{red}{x_{0}}$ de su dominio, cuando

$$\bbox[5px,border:2px solid red]{\lim_{x\rightarrow \color{red}{x_{0}}}\color{blue}{f(x)}=\color{blue}{f(}\color{red}{x_{0}}\color{blue}{)}}$$

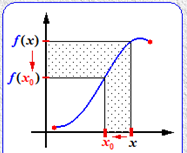
Esto significa, que los puntos «cercanos» a $\color{red}{x_{0}}$ son mandados por $\color{blue}{f}$ cerca de $\color{blue}{f(}$$\color{red}{x_{0}}$$\color{blue}{)}$
Se dice que $\color{blue}{f}$ es continua cuando $\color{blue}{f}$ es continua en cada uno de los puntos de su

$$\bbox[5px,border:2px solid red]{dominio}$$

8 Junio 2016, Creado con GeoGebra

• 
• 
• 

Comparte esto:

• Haz clic para compartir en Facebook (Se abre en una ventana nueva)
• Haz clic para compartir en Twitter (Se abre en una ventana nueva)
• Haz clic para compartir en WhatsApp (Se abre en una ventana nueva)
• Haz clic para compartir en LinkedIn (Se abre en una ventana nueva)
• Haz clic para enviar un enlace por correo electrónico a un amigo (Se abre en una ventana nueva)

Me gusta esto:

Me gusta Cargando...