Introducción
En esta entrada introduciremos un nuevo concepto: el de familias coaxiales. Veremos cómo se relaciona este concepto con el de eje radical.
Familias coaxiales
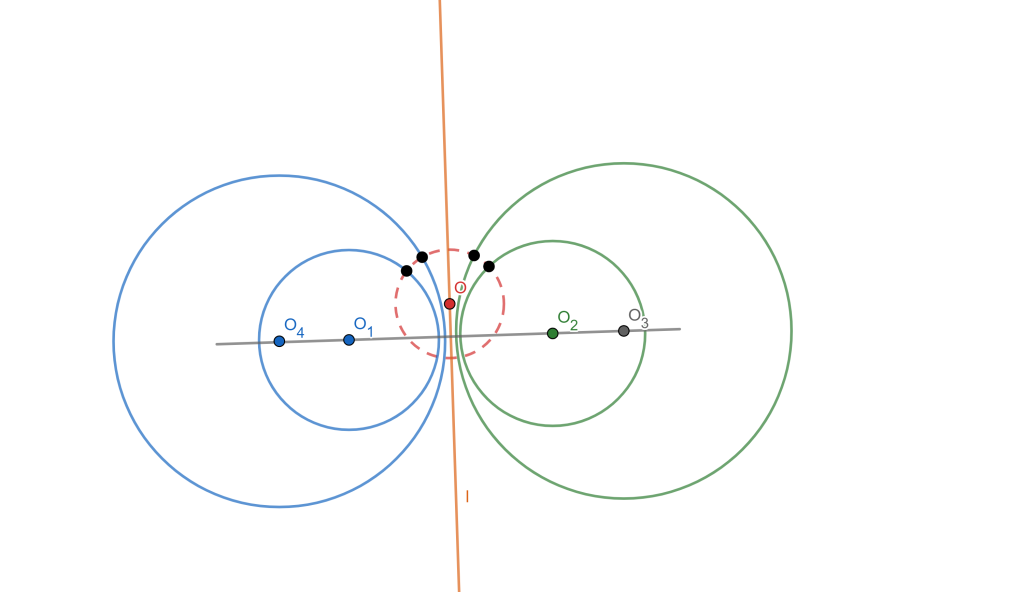
Definición. Un conjunto de círculos se llaman (Familias Coaxiales) círculos coaxiales si y solo si existe una recta llamada eje radical, que además es el eje radical de cada par de círculos del conjunto.
Además, como el eje radical de 2 circunferencias es ortogonal a la línea de los centros, entonces los centros de las circunferencias del sistema coaxial de circunferencias son colineales.
Se tienen distintas propiedades:
- Si dos círculos de un conjunto coaxial son tangentes, todos los círculos del conjunto son tangentes.
- Si dos círculos de un conjunto coaxial se intersecan en dos puntos, todos los círculos del conjunto pasan por estos dos puntos.
- El eje radical de un conjunto coaxial es el lugar geométrico de los puntos cuya potencia respecto a todos los círculos del conjunto son iguales.
- Dos circunferencias pertenecen a una única familia coaxial.
- Dos circunferencias determinan una única familia coaxial.
- Si dos puntos tienen la misma potencia respecto a 3 circunferencias, entonces las circunferencias son coaxiales.
- Si una circunferencia corta ortogonalmente a 2 circunferencias de un sistema coaxial, entonces corta ortogonalmente a todos los círculos del sistema coaxial.
- Dado un conjunto coaxial de círculos, entonces el conjunto de círculos ortogonales a estos círculos forman un conjunto coaxial de círculos.
Proposición. Sea una familia de circunferencias con centros colineales. Estas son un sistema coaxial de circunferencias si y solo si existe una circunferencia ortogonal a todas ellas.
Denotaremos como ${\{C_i\}}^n_{i=1}$ una familia de circunferencias con centros colineales.
Demostración.
$\boldsymbol{\Rightarrow}]$
Denotemos $l$ al eje radical. Sea $C(O,r)$ una circunferencia donde $O$ está en $l$ y además $C(O,r)$ es ortogonal a $\mathcal{C}_1$ una circunferencia del sistema.
Ahora, como $O$ está en $l$ y $C(O,r)$ es ortogonal a $\mathcal{C}_1$, usando la proposición: Si el centro de una circunferencia está en el eje radical de 2 circunferencias dadas y es ortogonal a una de ellas, entonces la circunferencia es ortogonal también a la otra. Por lo cual $C(O,r)$ es ortogonal a cada circunferencia de ${\{C_i\}}^n_{i=1}$. $\lrcorner$
$\boldsymbol{\Leftarrow} ]$
Sea $C(O,r)$ una circunferencia ortogonal a ${\{C_i\}}^n_{i=1}$. Además, $C(O,r)$ es ortogonal a $\mathcal{C}_1$ y $\mathcal{C}_2$ donde $\mathcal{C}_1$ y $\mathcal{C}_2$ pertenecen a ${\{C_i\}}^n_{i=1}$.
Llamemos a $l$ el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$, sabemos que $l$ es ortogonal a la línea $O_1O_2$, y recordando la proposición: Si una circunferencia es ortogonal a 2 circunferencias dadas, entonces su centro está en el eje radical de las 2 circunferencias, por lo cual $O$ está en $l$. Como $O_1, O_2, … , O_n$ son puntos colineales y los ejes radicales de cada par de circunferencias son líneas perpendiculares a $O_1O_2$ que pasan por $O$, entonces $l$ es el eje radical de cada par de circunferencias.
$\therefore$ ${\{C_i\}}^n_{i=1}$ es un sistema de circunferencias coaxiales. $\square$
Existen 3 tipos de sistemas de (Familias Coaxiales) circunferencias coaxiales: tangentes, que se intersecan y ajenas.
Circunferencias coaxiales tangentes
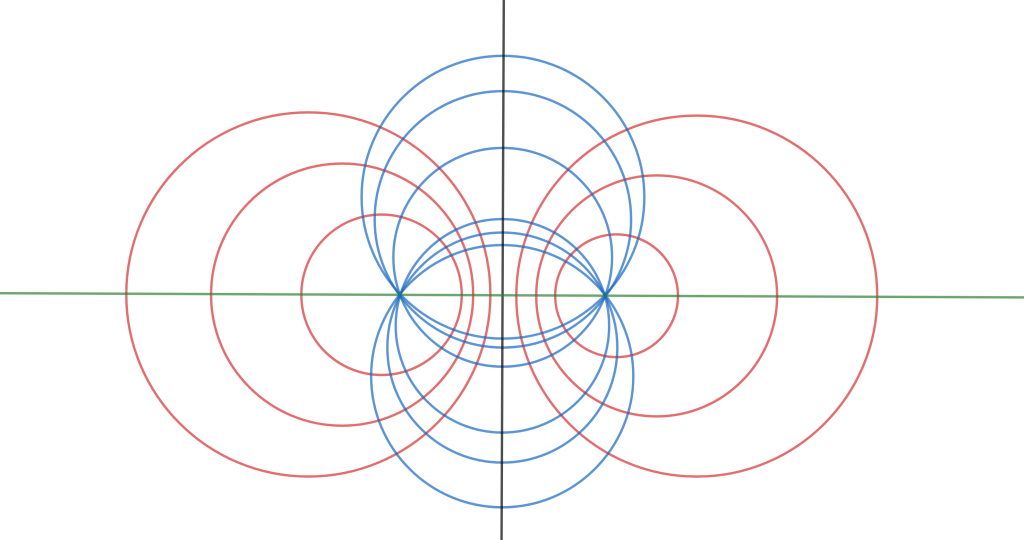
Se tiene un sistema de circunferencias coaxiales tangentes, además la familia de circunferencias con centro en el eje radical del sistema y que son ortogonales a todas y cada una de las circunferencias del sistema, también forman otro sistema coaxial de circunferencias tangentes.
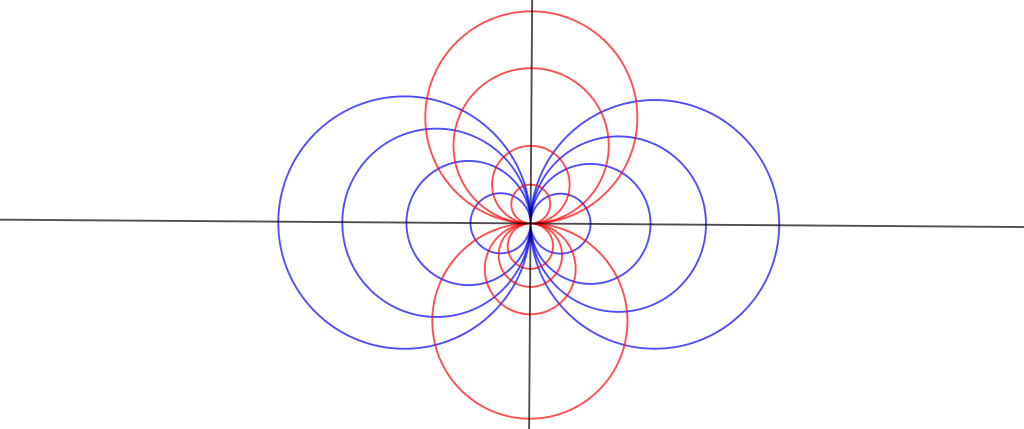
Circunferencias coaxiales que se intersectan
Se tiene un sistema de circunferencias coaxiales que se intersecan en 2 puntos, la familia de circunferencias con centro en el eje radical del sistema y que son ortogonales a todas las circunferencias del sistema, forman un sistema coaxial de circunferencias ajenas.
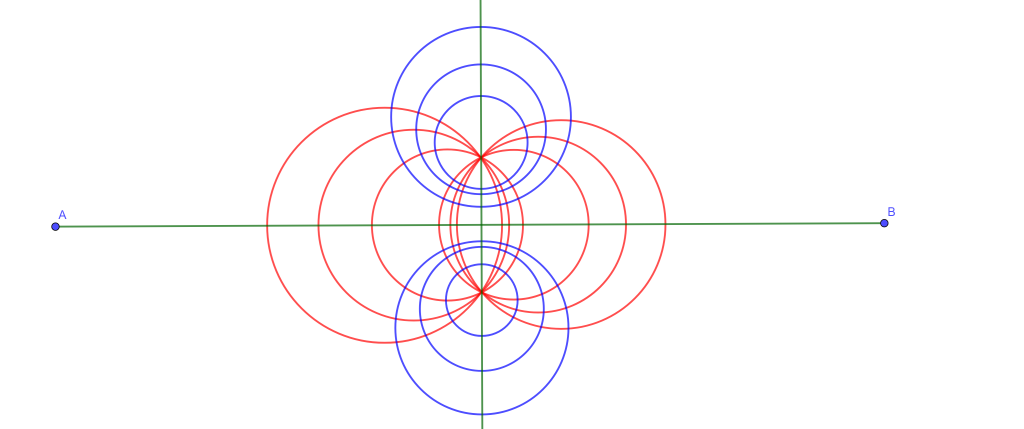
Circunferencias coaxiales ajenas
Se tiene un sistema de circunferencias coaxiales ajenas, la familia de circunferencias con centro en el eje radical del sistema y que son ortogonales a todas las circunferencias del sistema, forman un sistema coaxial de circunferencias que se intersecan.
Más adelante…
Se abordará en la siguiente entrada la circunferencia de similitud.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Circunferencias ortogonales
- Siguiente entrada del curso: Circunferencias de similitud