Introducción
Una función vectorial es una función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ ó $f:\mathbb{R}\rightarrow\mathbb{R}^{3}$ de la forma
$$f(t)=x(t)i+y(t)j~~\acute{o}~~f(t)=x(t)i+y(t)j+z(t)k$$
donde las funciones componentes $x(t)$, $y(t)$ y $z(t)$ son funciones de valor real del parámetro t. Las funciones con valores vectoriales son también escritas en forma
$$f(t)=(x(t),y(t))~\acute{o}~f(t)=(x(t),y(t),z(t))$$
En ambos casos, la primera forma de la función define una función vectorial bidimensional; la segunda forma describe una función vectorial tridimensional.
En el siguiente applet desarrollado en Geogebra, podrás manipular un parametro d, dentro de un intervalo $[a,b]$, de tal manera que podrás observar como se va dibujando una curva en el plano.
De acuerdo al applet, el parámetro $d$ puede estar entre dos números reales: $a \leq d \leq b$. Otra posibilidad es que el valor de d tome todos los numeros reales. Las funciones de los componentes en sí mismas pueden tener restricciones de dominio que imponen restricciones en el valor de t. A menudo usamos $t$ como parámetro porque $t$ puede representar el tiempo.
Las rectas en el plano, las podemos pensar como un conjunto definido de la siguiente forma:
$$\ell=\left\{(x,y)\in\mathbb{R}^{2}~\Big{|}~ax+by+c=0\right\}$$
Si $a\neq 0$ entonces para cualquier $(x,y)\in\ell$ se tiene
$$x=\frac{-c-by}{a}$$
Por tanto, a la pareja $(x,y)$ la podemos escribir como
$$\left(\frac{-c-by}{a},y\right)$$
es decir, la podemos escribir en términos de una sola variable. Por lo que si consideramos la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$f(t)=\left(\frac{-c-bt}{a},t\right)$$
se cumple que $f(\mathbb{R})=\ell$, es decir, que la imagen de la función es toda la recta.
En efecto, para cualquier elemento $t$ en $f(\mathbb{R})$ se cumple
$$a\left(\frac{-c-bt}{a}\right)+bt+c=(-c-bt)+bt+c=0$$
con lo cual concluimos $f(\mathbb{R})\subset \ell$. Por otra parte, si $(x,y)\in\ell$, basta tomar $t=y$ para que se cumpla
$$f(y)=\left(\frac{-c-by}{a},y\right)=(x,y)$$
con lo que concluimos que $\ell\subset f(\mathbb{R})$ y por lo tanto $f((\mathbb{R}))=\ell$.$~~\blacksquare$
Con un razonamiento similar se puede probar que la circunferencia con centro en el origen y radio $r$, se puede describir como el conjunto
$$C_{r}=\left\{(x,y)\in\mathbb{R}^{2}~\Big{|}~x^{2}+y^{2}=r^{2}\right\}$$
y dicho conjunto se puede obtener como la imagen de la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$f(t)=(r\cos(t),r\sin(t)),~~t\in[0,2\pi].~~\blacksquare$$
Con un razonamiento similar se puede probar que la elipse, se puede describir como el conjunto
$$E=\left\{(x,y)\in\mathbb{R}^{2}~\Big{|}~\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\right\}$$
y dicho conjunto se puede obtener como la imagen de la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$\boxed{f(t)=(a\cos(t),b\sin(t)),~~t\in[0,2\pi].}$$ $\blacksquare$
En general si un subconjunto $C\subset \mathbb{R}^{n}$ es tal que coincide con la imagen de una función $f:\mathbb{R}\rightarrow\mathbb{R}^{n}$, diremos que dicha función es una parametrización de C.
Definición. Sea $C\subset\mathbb{R}^{n}$. Si existe $\gamma=(\gamma_{1},\gamma_{2},…,\gamma_{n}):\mathbb{R}\rightarrow\mathbb{R}^{n}$ tal que $\gamma(I)=C$ decimos que $\gamma$ es una parametrización de C. En tal caso diremos que las ecuaciones
\begin{align*} x_{1} & =\gamma_{1}(t) \\ x_{2} & =\gamma_{2}(t) \\ \vdots & =\vdots \\ x_{n} & =\gamma_{n}(t) \end{align*}
son unas ecuaciones paramétricas de C.
Ejemplo. Si $f$ es la función vectorial por $f(t)=(2\cos(t),2\sin(t))$ con $t\in[0,2\pi]$, tenemos entonces que $f$ asocia a cada número real $t$ en el intervalo $[0,2\pi]$, un par ordenado $(x,y)$ con $x=2\cos t$ y $y=2\sin t$, que son las ecuaciones paramétricas de una circunferencia de radio 2 y centro en el origen. Asi pues la gráfica de $f$ es una circunferencia.
Cada una de las funciones vectoriales que se dan a continuación,
define el mismo lugar geométrico o una parte de éste; sin embargo,
el sentido, el punto de partida y la rapidez de recorrido así como
la porción de la curva que se considera en cada caso varia.
\begin{align*} f_{1}(t) &=(2\cos t, 2\sin t) \quad t\in[0,2\pi] \\ f_{2}(t) &=(2\cos t, 2\sin t) \quad t\in[0,\pi] \\ f_{3}(t) &=(2\cos 3t, 2\sin 3t) \quad t\in[0,2\pi] \\ f_{4}(t) &=(2\cos t, 2\sin t) \quad t\in[0,\pi] \\f_{5}(t) &=(2\cos t, 2\sin t) \quad t\in[0,6\pi] \\ f_{6}(t) &=(2\cos t, 2\sin t) \quad t\in[-\pi,\pi] \end{align*}
Para una función vectorial en $\mathbb{R}^{3}$ decimos que: Si $D$ es un conjunto de $\mathbb{R}$, entonces $f(t)$ es una función vectorial con dominio $D$ si y sólo si, para todo $t\,\epsilon\,D$
$$f(t)=x_{1}(t)i+x_{2}(t)j+x_{3}(t)k$$
donde $x_{1}(t),x_{2}(t)$ y $x_{3}(t)$ son funciones escalares con dominio $D$. $\blacksquare$
Ejemplo. Que representa la función vectorial cuyas ecuaciones parametricas son:
$$f(t)=\left(\frac{1-t^{2}}{1+t^{2}},\frac{2t}{1+t^{2}}\right)$$
En este caso haciendo la sustitución $\displaystyle{t=\tan\left(\frac{u}{2}\right)}$ se tiene que
$$\frac{1-t^{2}}{1+t^{2}}=\frac{1-\tan^{2}\left(\frac{u}{2}\right)}{1+\tan^{2}\left(\frac{u}{2}\right)}=\frac{1-\frac{\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}{1+\frac{\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}=\frac{\frac{\cos^{2}\left(\frac{u}{2}\right)-\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}{\frac{\cos^{2}\left(\frac{u}{2}\right)+\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}=\frac{\cos^{2}\left(\frac{u}{2}\right)-\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)+\sin^{2}\left(\frac{u}{2}\right)}=\cos^{2}\left(\frac{u}{2}\right)-\sin^{2}\left(\frac{u}{2}\right)$$
$$=\cos\left(\frac{2u}{2}\right)=\cos(u)$$
$$\frac{2t}{1+t^{2}}=\frac{2\tan\left(\frac{u}{2}\right)}{1+\tan^{2}\left(\frac{u}{2}\right)}=2\frac{\frac{\sin\left(\frac{u}{2}\right)}{\cos\left(\frac{u}{2}\right)}}{1+\frac{\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}=2\frac{\frac{\sin\left(\frac{u}{2}\right)}{\cos\left(\frac{u}{2}\right)}}{\frac{\cos^{2}\left(\frac{u}{2}\right)+\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}=2\sin\left(\frac{u}{2}\right)\cos\left(\frac{u}{2}\right)=\sin\left(\frac{2u}{2}\right)=\sin(u)$$
donde $u\in[0,\pi]$. Al ser
$$\left(\frac{1-t^{2}}{1+t^{2}}\right)^{2}+\left(\frac{2t}{1+t^{2}}\right)^{2}=\cos^{2}(u)+\sin^{2}(u)=1$$ se trata de una circunferencia de radio 1 con centro en el origen. $\blacksquare$
Ejemplo.Parametrización de la curva Cicloide.
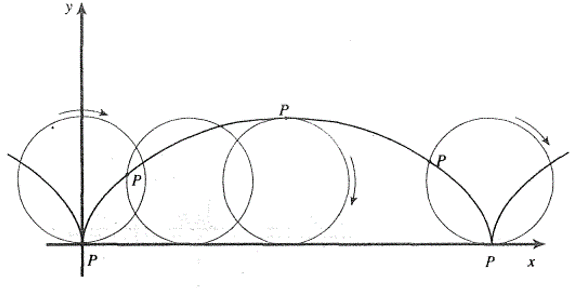
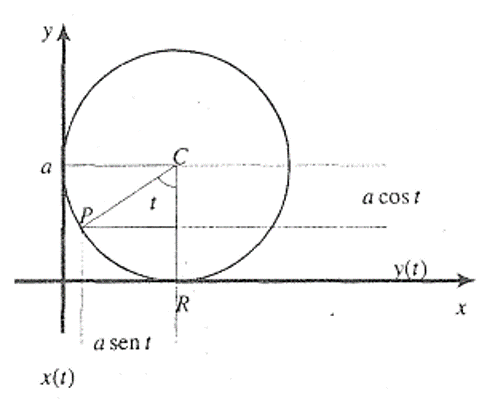
Supongamos que un círculo de radio a rueda sin deslizarse a lo largo de una línea recta horizontal. Encuentre la curva descrita por un punto fijo P de su circunferencia.
Sea t el ángulo en radianes, que forma (la línea que contiene) el radio CP con la línea CR.
Nótese que $OR$ es justamente la longitud de arco RP que es igual a $at$, de modo que el punto C tiene coordenadas $C=(at,a)$. Si $(x(t),y(t))$ denotan las coordenadas del punto p, se tiene
$$x(t)=at+a\sin(t)$$
$$y(t)=a+a\cos(t)$$
Por lo que la cicloide se puede representar por la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$f(t)=(at+a\sin(t),a+a\cos(t))$$
Si se despeja la variable t en la ecuación paramétrica, se obtendrá la forma cartesiana:
$$x=a\arcsin\left(\frac{y}{a}-1\right)+\left(y-a\right)$$. $\blacksquare$
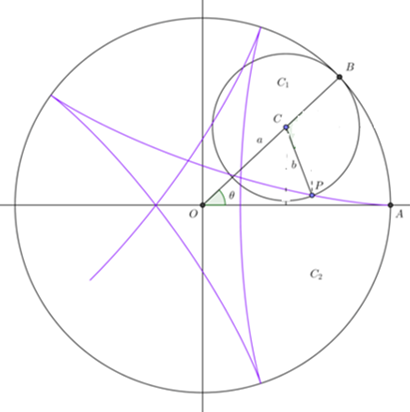
Ejemplo. Parametrización de la curva Epicicloide.
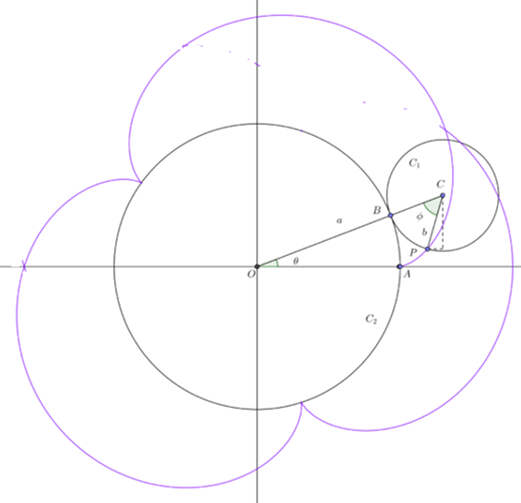
Supongamos que un círculo de radio a rueda sin deslizarse sobre una circunferencia. Encuentre la curva descrita por un punto fijo $P$ de su circunferencia.
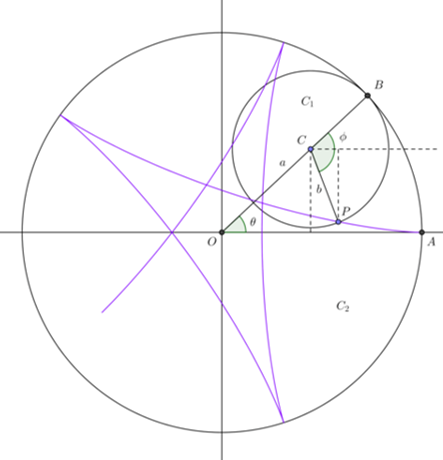
De acuerdo a la siguiente figura
\begin{align*}\cos(\theta) & =\frac{x_{c1}}{a+b}&\Rightarrow~x_{c1}=(a+b)\cos(\theta) \\sin(\theta) & =\frac{y_{c1}}{a+b}&\Rightarrow~y_{c1}=(a+b)\sin(\theta)\end{align*}
También se tiene que el arco de circulo $C_{1}PB$ es igual al arco de circulo $C_{2}AB$ esto es
$$a\theta=b\phi~\Rightarrow~\frac{a}{b}\theta=\phi$$
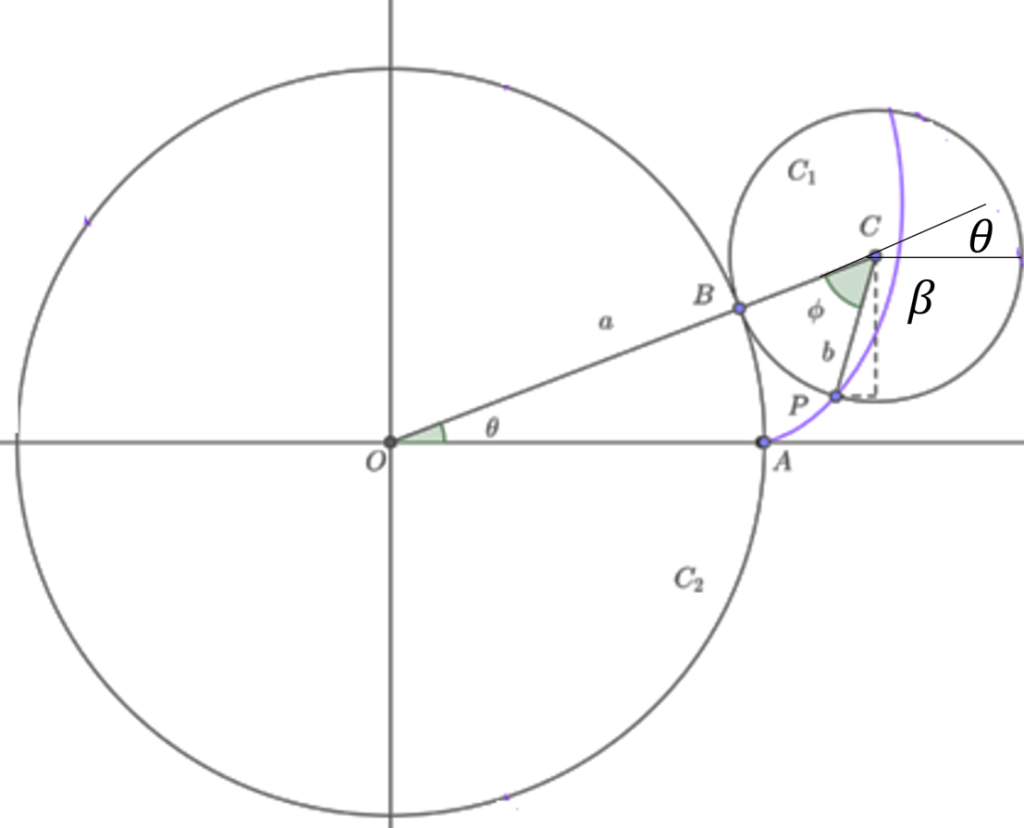
Ahora de acuerdo a la figura
$$\theta+\phi-\beta=\pi~\Rightarrow~\beta=\pi-\theta+\phi$$
Por lo que usando que $\cos$ es par
\begin{align*} P\in C_{1} &~\Leftrightarrow~P\in (b\cos(\beta),b\sin(\beta)) \\ &~\Leftrightarrow~P\in (b\cos(\theta+\phi-\pi),b\sin(\theta+\phi-\pi)) \\ &~\Leftrightarrow~P\in (-b\cos(\theta+\phi),-b\sin(\theta+\phi)) \end{align*}
Utilizando todo lo anterior
\begin{align*} x & =\left((a+b)\cos(\theta)-b\cos(\theta+\phi)\right) \\ y & =\left((a+b)\sin(\theta)-b\sin(\theta+\phi)\right) \end{align*}
Como $\displaystyle{\frac{a}{b}\theta=\phi}$ tenemos
\begin{align*} x & =\left((a+b)\cos(\theta)-b\cos\left(\theta+\frac{a}{b}\theta\right)\right) \\ y & =\left((a+b)\sin(\theta)-b\sin\left(\theta+\frac{a}{b}\theta\right)\right) \end{align*}
Por lo que la Epicicloide se puede representar por la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$f(\theta)=\left((a+b)\cos(\theta)-b\cos\left(\theta+\frac{a}{b}\theta\right),(a+b)\sin(\theta)-b\sin\left(\theta+\frac{a}{b}\theta\right)\right)$$ $\blacksquare$
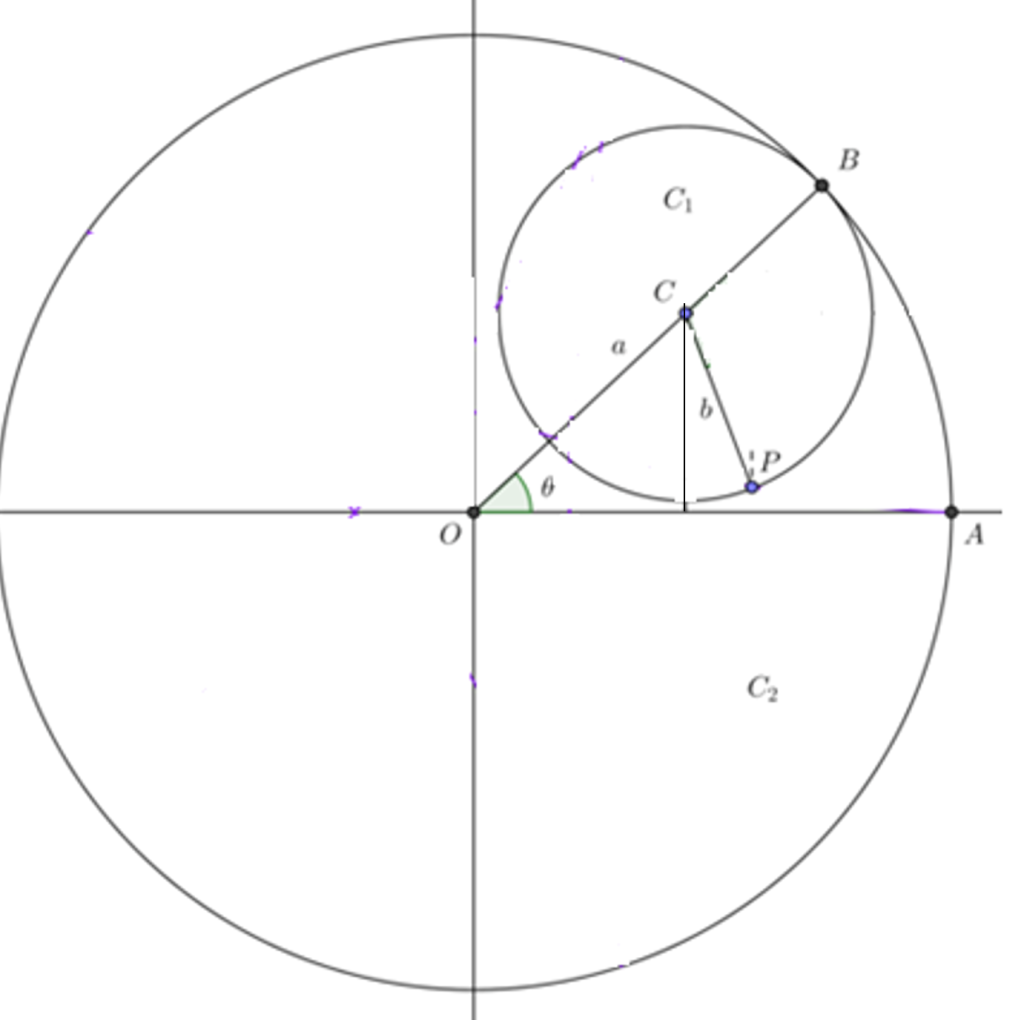
Ejemplo. Parametrización de la curva Hipocicloide.
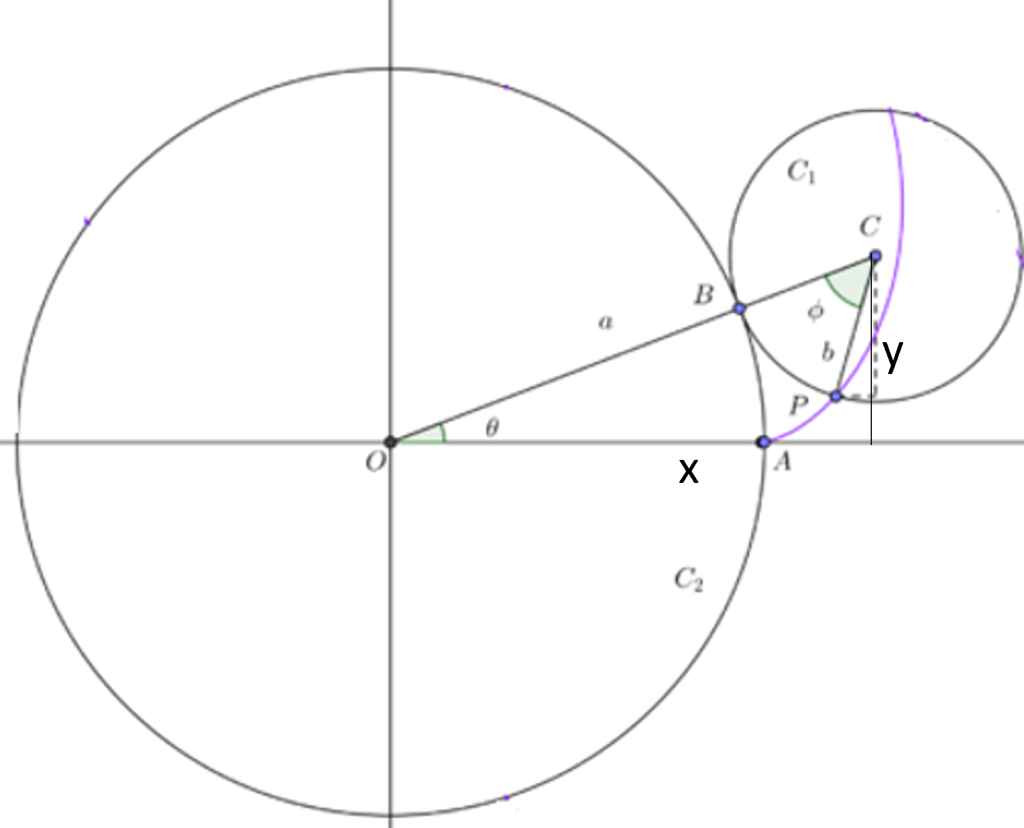
Una curva hipocicloide es la trayectoria descrita por un punto P situado sobre una circunferencia que rueda sin deslizar por el interior de otra circunferencia.
De acuerdo a la siguiente figura se tiene
\begin{align*} \cos(\theta) & =\frac{x}{a-b}&\Rightarrow~x=(a-b)\cos(\theta) \\sin(\theta) & =\frac{y}{a-b}&\Rightarrow~y=(a-b)\sin(\theta) \end{align*}
También se tiene que el arco de circulo $C_{1}PB$ es igual al arco de circulo $C_{2}AB$ esto es
$$a\theta=b\phi~\Rightarrow~\frac{a}{b}\theta=\phi$$
Ahora de acuerdo a la figura
$$\phi-\theta=\frac{a}{b}\theta-\theta$$
Utilizando todo lo anterior
\begin{align*} x & =\left((a-b)\cos(\theta)+b\cos(\phi-\theta)\right) \ y & =\left((a+b)\sin(\theta)-b\sin(\phi-\theta)\right) \end{align*}
Como $\displaystyle{\frac{a}{b}\theta=\phi}$ tenemos
\begin{align*} x & =\left((a-b)\cos(\theta)+b\cos\left(\frac{a}{b}\theta-\theta\right)\right) \ y & =\left((a+b)\sin(\theta)-b\sin\left(\frac{a}{b}\theta-\theta\right)\right) \end{align*}
Por lo que la Epicicloide se puede representar por la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$f(\theta)=\left((a-b)\cos(\theta)+b\cos\left(\frac{a}{b}\theta-\theta\right),(a-b)\sin(\theta)-b\sin\left(\frac{a}{b}\theta-\theta\right)\right)$$. $\blacksquare$
Funciones vectoriales $f:\mathbb{R}\rightarrow\mathbb{R}^{3}$
Supongamos el espacio tridimensional $\mathbb{R}^{3}$ dotado del sistema de coordenadas $(x,y,z)$. Una curva C parametrizada en este espacio es la representación gráfica de una función vectorial:
$$r(t)=(x(t),y(t),z(t))$$
donde t se denomina el parámetro de una curva, $t\in\mathbb{R}$. La estructura de la
curva dependerá de las funciones $x(t), y(t)~ y~z(t)$.
Ejemplo. Describa la curva definida por la función vectorial $r(t)=(1+t,2+5t,-1+6t)$.
En este caso las ecuaciones paramétricas correspondiente son, $x=1+t$,
$y=2+5t$, $z=1+6t$ o sea $r(t)=(1,2,-1)+t(1,5,6)$
se trata de una recta que pasa por $(1,2,-1)$ y es paralela a $(1,5,6)$.$\blacksquare$
Ejemplo. Dibuje la curva cuya ecuación vectorial es $r(t)=2\cos ti+\sin tj+tk$.
En este caso, las ecuaciones paramétricas para esta curva son, $x=2\cos t$, $y=\sin t$, $z=t$, por lo que $\displaystyle{x/2=\cos t}$
$\therefore$ $\qquad$ $\displaystyle{\left(\frac{x}{2}\right)^{2}+y^{2}=1}$ la curva se encuentra en el cilindro elíptico $\displaystyle{\left(\frac{x^{2}}{4}\right)^{2}+y^{2}=1}$. Ya que $z=t$ la curva forma una espiral ascendente alrededor del cilindro conforme $t$ se incrementa
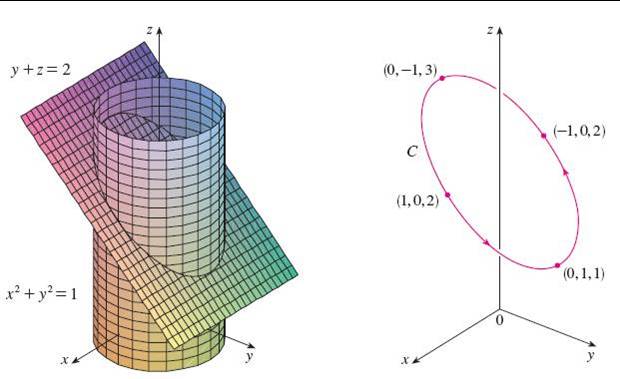
Ejemplo. Halle una función vectorial que represente la curva de la intersección del cilindro $x^{2}+y^{2}=1$ y el plano $y+z=2$.
En este caso la figura muestra la forma en que se cruzan, el plano y el cilindro, así mismo la figura ilustra la curva de intersección.
La proyección $C$ sobre el plano $xy$ es el circulo $x^{2}+y^{2}=1$, $z=0$, que podemos parametrizar como $x=\cos t$, $y=\sin t$, $0\leq t \leq 2\pi$, con base en la ecuacion del plano, tenemos que $$z=2-y=2-\sin t$$
$\therefore~~~x=\cos t,~~y=\sin t,~~z=2-\sin t,~~~0\leq t \leq 2\pi$
$\therefore$ la ecuación vectorial correspondiente es
$$r(t)=\cos ti+\sin tj+(2-\sin t)k \qquad 0\leq t \leq 2\pi$$ $\blacksquare$
Dominio de la Función Vectorial
El dominio de una función vectorial $r(t)$ es el conjunto de valores permitidos de $t$. Si $r(t)$ se define en términos de las funciones de las componentes y no se especifica explícitamente el dominio, entonces se sobreentiende que el dominio es la intersección de los dominios naturales de las funciones de las componentes, por lo que éste recibe el nombre de dominio natural de $r(t)$.
Sea $f(t)=(x_{1}(t)),x_{2}(t)),…,x_{n}(t))~\in\mathbb{R}^{n}$ entonces el $\displaystyle{Dom_{f}=\bigcap_{i=1}^{n} Dom_{x_{i}}}$
Ejemplo. Halle el dominio de la función vectorial
$$f(t)=\left(t^{2},\sqrt{t-1},\sqrt{5-t}\right)$$
tenemos que
\[Si\quad x_{1}(t)=t^{2}\quad entonces\quad \textit{Dom} (x_{1}(t))=\{\mathbb{R}\}\]
\[Si\quad x_{2}(t)=\sqrt{t-1}\quad entonces\quad \textit{Dom} (x_{2}(t))=\{t\in\mathbb{R}~|~t\geq1\}\]
\[Si\quad x_{3}(t)=\sqrt{5-t}\quad entonces\quad \textit{Dom} (x_{3}(t))=\{t\in\mathbb{R}~|~5\geq t\}\]
Por lo tanto
\[\textit{Dom} (f(t))=\bigcap{\textit{Dom} (x_{1}(t)),\textit{Dom} (x_{2}(t)),\textit{Dom} (x_{3}(t))}=\{t\in\mathbb{R}~|~1~\leq t~\leq 5\} \]. $\blacksquare$
Halle el dominio de la función vectorial
$$f(t)=\left(Ln(t),\frac{t}{t-1},e^{-t}\right)$$
tenemos que
\[Si\quad x_{1}(t)=Ln(t)\quad entonces\quad \textit{Dom} (x_{1}(t))=\{t\in\mathbb{R}|0<t\}\]
\[Si\quad x_{2}(t)=\frac{t}{t-1}\quad entonces\quad \textit{Dom} (x_{2}(t))=\{t\in\mathbb{R}|1\neq t\}\]
\[Si\quad x_{3}(t)=e^{-t}\quad entonces\quad \textit{Dom} (x_{3}(t))=\{\mathbb{R}\}\]
Por lo tanto
\[\textit{Dom} (f(t))=\bigcap{\textit{Dom} (x_{1}(t)),\textit{Dom} (x_{2}(t)),\textit{Dom} (x_{3}(t))}=\{t\in\mathbb{R}~|~0< t,\quad t\neq1\} \].$$\blacksquare$$
Graficar funciones con valores vectoriales
Recuerda que un vector plano consta de dos cantidades: dirección y magnitud. Dado cualquier punto en el plano (el punto inicial), si nos movemos en una dirección específica por una distancia específica, llegamos a un segundo punto. Esto representa el punto final de el vector. Calculamos las componentes del vector restando las coordenadas del punto inicial a las coordenadas del punto terminal.
Se considera que un vector está en posición estándar si el punto inicial se encuentra en el origen. Al graficar un valor vectorial, por lo general, representamos gráficamente los vectores en el dominio de la función en la posición estándar, porque hacerlo garantiza la unicidad de la gráfica. Esta convención se aplica también a las gráficas de funciones vectoriales tridimensionales.
La gráfica de una función vectorial de la forma $r(t)=f(t)i+g(t)j$ consiste en el conjunto de todos $(t,r(t))$, y la ruta que traza se llama curva plana.
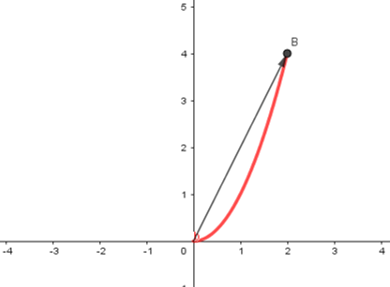
La gráfica de una función vectorial de la forma $r(t) = f(t)i + g(t)j + h(t)k$ consiste en el conjunto de todos $(t, r(t))$, y el camino que traza se llama curva espacial.
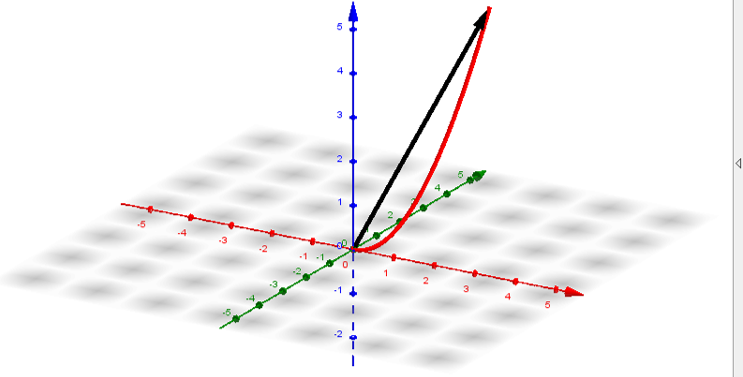
Cualquier representación de una curva plana o una curva espacial utilizando un valor vectorial se denomina parametrización vectorial de la curva.
Ejemplo. Cree una gráfica de la siguiente funcion con valores vectoriales:
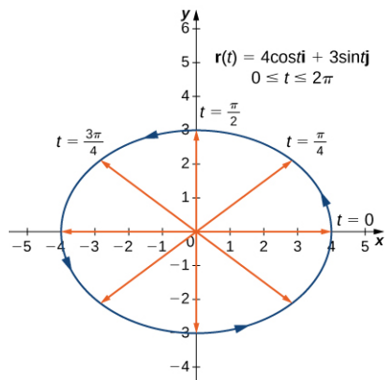
$$r(t)=4\cos(t)i+3\sin(t)j,~~~0\leq t\leq 2\pi$$
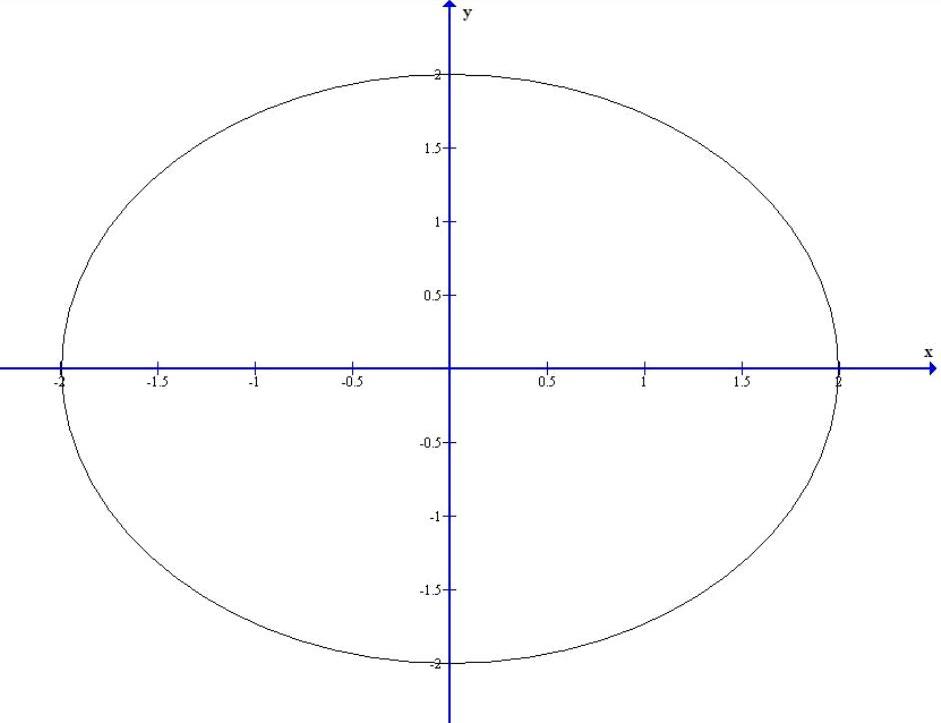
Como con cualquier gráfico, comenzamos con una tabla de valores. Luego graficamos cada uno de los vectores en la segunda columna en posición estándar y conectamos los puntos terminales de cada vector para formar una curva. Esta curva resulta ser una elipse centrada en el origen.
Ejemplo. Cree una gráfica de la siguiente funcion con valores vectoriales:
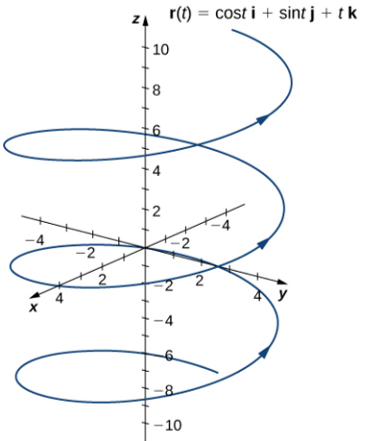
$$r(t)=\cos(t)i+\sin(t)j+tk,~~~0\leq t\leq 4\pi$$
Realizamos el mismo procedimiento para una función vectorial tridimensional.
Los valores luego se repiten, excepto por el hecho de que el coeficiente de k siempre es creciente. Esta curva se llama hélice. Observe que si se elimina la componente k, entonces la función se convierte en $r(t)=\cos(t)i+\sin(t)j$, que es un círculo unitario centrado en el origen.
Operaciones con Funciones Vectoriales
Las operaciones usuales del algebra vectorial pueden aplicarse para
combinar 2 funciones o una función vectorial con una función real.
Si $f$ y $g$ son funciones vectoriales y si $u$ es una función real, teniendo todas un dominio común, definimos nuevas funciones $F+G$, $uF$ y $F\cdot G$ mediante
\begin{align*}
(F+G)(t)&=F(t)+G(t)\\
u~F(t)&=u(t)~F(t)\\
(F\cdot G) (t)&= F(t)\cdot G(t)\\
(F\times G )(t)&=F(t)\times G(t)~si~F,G\in \mathbb{R}^{3}
\end{align*}
Más adelante
Una vez definido el concepto de función vectorial vamos a aprender a calcular el límite de estas funciones. Cuando calculamos el límite de una sola variable basta que coincidan los límites laterales para saber que existe, pero cuando lo hacemos en más dimensiones tenemos más direcciones de aproximación.
Tarea moral
1.- Sobre la parte exterior de una circunferencia fija de radio a rueda (sin resbalar) otra circunferencia de radio b. Encuentre una función de $\mathbb{R}$ en $\mathbb{R}^{2}$ que describa el movimiento de un punto que se encuentre en la cicunferencia exterior.
2.- Sea $R \subset \mathbb{R}^{2}$ la recta cuya ecuación cartesiana es $ax+by+c=0$ (con $a^2+b^2>0$). Muestra que si $\overline{x_0}=(x_0,y_0)$ y $\overline{x_1}=(x_1,y_1)$ son dos puntos diferentes que pertenecen a $\mathbb{R}$ entonces la función $f(t): \mathbb{R} \rightarrow \mathbb{R^2}$ dada por $f(t)= \overline{x_0} +t( \overline{x_1}- \overline{x_0})$ es una parametrización de $R$
3.- Halla el dominio de la siguiente función vectorial $f:\mathbb{R}\rightarrow \mathbb{R^3}$ donde $f(t)=(t^2, ln(t-2), \sqrt{4-t})$
4.- Dadas las funciones vectoriales $f(t)=(1+t,t^2)$, $g(t)=(t, t^3)$ halla $(fg)(t)$
5.- Crea la gráfica de la siguiente función vectorial $r(t)=(t^2-1)i+(2t-3)j$, $0 \leq t \leq 3$
Enlaces
En el siguiente enlace podrás conocer algunas curvas paramétricas famosas
El siguiente enlace presenta un archivo de Google Colab mostrando una visualización en python de las curvas paramétricas elipse y hélice.
https://colab.research.google.com/drive/1zf9sei2Nyfa2GqiGHEapCNJbBI701z9P?usp=sharing
En el caso de la elipse puedes contestar:
¿Qué pasa cuando $a=b$
¿Qué pasa cuando $a \neq b$
El siguiente enlace te llevará a una página sobre decenas de curvas conocidas y estudiadas.


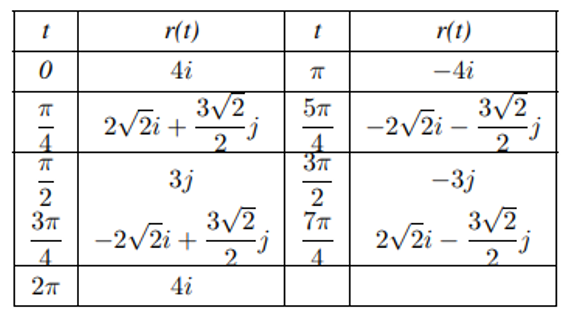

Hola, buenas noches.
Estaba leyendo esta entrada y quisiera hacer un par de comentarios:
Cuando demuestras que el conjunto l (la recta) coincide con la imagen de la función que das ahí, escribes que f(t)=l. Esta notación me confundió porque lo que quería decir en realidad que el conjunto de todos los puntos f(t) coincide con el conjunto l. En varios renglones no se hace esta distinción que me parece importante.
En la parametrización de la curva epicicloide ¿podría haber un poco más de desarrollo en el paso donde se introduce el ángulo beta? No terminó de quedarme claro por qué se resta y da pi en vez de sumarse y que dé pi.
En la parte del dominio de una función vectorial, creo que el dominio de la función en general está mal escrito, pues aparece que es la intersección de las funciones; yo pensaría que es la intersección de todos los dominios de cada función, por cómo se desarrolla en los ejemplos inmediatos.
Gracias de antemano por leer estos comentarios y gracias por el útil contenido. 🙂
Hola Zoe. Gracias por el comentario. Le eché un ojo y en efecto se debe decir mejor lo de la recta. Esa parte ya quedó arreglada, diciendo que f(R) es toda la recta. Quizás ese problema aparezca en otros lados, si lo encuentras, avísanos, porfa. Lo del dominio, también ya quedó mejor escrito en símbolos. De lo de la epicicloide, le aviso al Prof. Rubén Hurtado, que escribió la entrada originalmente, para que le eche un ojo.