MATERIAL EN REVISIÓN
Introducción
En las entradas anteriores construimos la maquinaria teórica sobre la que podemos definir un nuevo concepto de integral: «La integral de Lebesgue». En esta entrada estudiaremos las funciones simples y cómo es que se pueden integrar.
Las funciones simples son simplemente aquellas que toman una cantidad finita de valores. Resultan ser «las funciones más sencillas que se pueden integrar».
Funciones simples
En esta sección, $X$ denota un conjunto arbitrario y $\mathcal{M}$ una $\sigma$-álgebra sobre $X$.
Definición. Decimos que $s:X\to [-\infty,\infty]$ es una función simple si toma solamente una cantidad finita de valores.
Si $s$ es simple, podemos escribir: $$s=\sum_{k=1}^{m}\alpha_k \chi_{A_k},$$ Donde $\alpha_1,\dots, \alpha_m$ son los distintos valores del rango de $s$ y $A_k=\{ x\in X \ | \ f(x)=\alpha_k \}=f^{-1}(A_k)$ son conjuntos ajenos. (Como es usual $\chi_A$ denota la función característica del conjunto $A$, i.e. $\chi_A(x)=1$ si $x\in A$ y $\chi_A(x)=0$ en otro caso).
Observación. Hay muchas formas de escribir una función simple como combinación lineal de funciones características. La anterior es sólo una de ellas. A estas expresiones las llamaremos representaciones.
Las funciones simples y medibles admiten representaciones muy particulares como muestra la siguiente proposición. La demostración es una consecuencia sencilla de las propiedades de las funciones medibles y se deja como tarea moral.
Proposición. Si $\mathcal{M}$ es una $\sigma$-álgebra sobre $X$, una función simple $s$ es $\mathcal{M}$-medible si y sólo si admite una representación $s=\sum_{k=1}^{m}\alpha_k \chi_{A_k}$, con $A_k\in \mathcal{M}$ para todo $k$.
Antes de definir de lleno la integral de una función simple, veremos una proposición muy útil que, en general, nos dice que podemos aproximar cualquier función medible con funciones simples.
Teorema. Supongamos que $f:X\to [-\infty, \infty]$ es $\mathcal{M}$ medible. Entonces existe una sucesión $s_1,s_2,\dots$ de funciones simples $\mathcal{M}$ medibles tales que $$\lim_{k\to \infty} s_k = f.$$ Si $f\geq 0$, podemos tomar la sucesión de modo que $0\leq s_1\leq s_2\ \leq \dots$. O más generalmente si $f$ es $\mathcal{M}$ medible, podemos tomar la sucesión de modo que $|s_1|\leq \ |s_2|\leq \dots$ . Si $f$ es acotada, podemos hacer que la convergencia sea uniforme.
Demostración. Supongamos primero que $f\geq 0$. La idea es sencilla: truncamos la función, cada vez más «finamente», cuidando que eventualmente podamos aproximar cualquier valor (por grande que sea) en el rango de $f$.
Para cada $k\in \mathbb{N}$, definamos la función simple:
\begin{equation*}
s_k(x)=
\begin{cases}
\frac{i-1}{2^k} & \text{si } \frac{i-1}{2^k}\leq f(x) < \frac{i}{2^k}; \ \ i=1,2,\dots,2^k k \\
k & \text{si } k \leq f(x).
\end{cases}
\end{equation*}
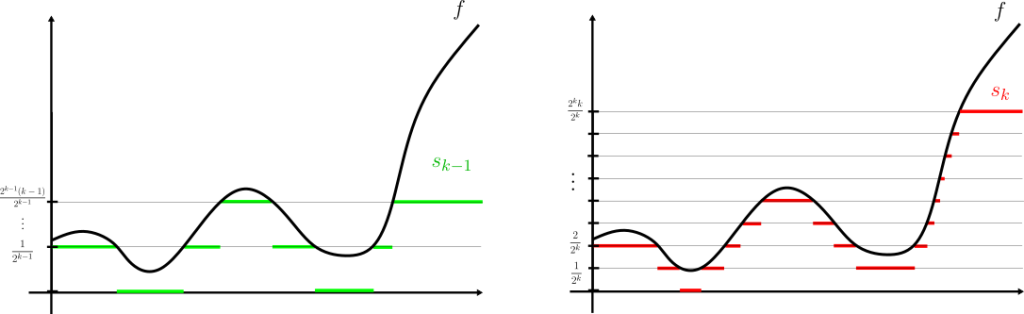
Como $f$ es $\mathcal{M}$ medible, los conjuntos $f^{-1}\left( [\frac{i-1}{2^k}, \frac{i}{2^k})\right)$ y $f^{-1}\left( [k,\infty] \right)$ son elementos de $\mathcal{M}$, de donde $s_k$ es medible.
Sea $x\in X$. Por un sencillo trabajo por casos, es fácil ver que $s_k(x)\leq s_{k+1}(x)$ para todo $k$ (si $f(x)\in [\frac{2i-2}{2^{k+1}}, \frac{2i-1}{2^{k+1}}) \subseteq [\frac{i-1}{2^k}, \frac{i}{2^k})$, $s_k(x)=s_{k+1}(x)$. En cualquier otro caso $s_k(x)<s_{k+1}(x)$).
Si $f(x)<\infty$, existe algún entero $N$ tal que $f(x)< N$. Luego, si $k\geq N$, por definición \begin{equation} f(x)\in \left[s_k(x), s_k(x)+\frac{1}{2^k}\right) \ \ \implies \ \ |f(x)-s_k(x)|<\frac{1}{2^k}. \end{equation} De donde $s_k(x)\longrightarrow f(x)$ cuando $k\longrightarrow \infty$. Si $f(x)=\infty$, $s_k(x)=k\longrightarrow \infty$ cuando $k\longrightarrow \infty$.
En todo caso, para cualquier $x\in X$ concluimos que $$\lim_{k\to \infty} s_k(x) = f(x).$$
Entonces $s_k$ es la sucesión buscada en este caso.
Veamos ahora el caso general. Notemos que $f=f_+-f_-$. Tomemos sucesiones de funciones simples $0\leq r_1\leq r_2\leq \dots$ y $0\leq t_1 \leq t_2\leq \dots$ que convergen puntualmente a $f_+$ y $f_-$ respectivamente definidas como en el caso anterior. Luego, para cada $k\in \mathbb{N}$, sea $$s_k=r_k-t_k.$$ Claramente es una sucesión de funciones simples tal que $s_k=r_k-t_k\longrightarrow f_+-f_-=f$ puntualmente cuando $k\longrightarrow \infty$.
Dado $x\in X$, si $f(x)\geq 0$, entonces, por construcción, $t_k(x)=0$ $\forall k$ $\implies$ $0\leq r_k(x)=s_k(x)$ $\forall k$. Se sigue que la sucesión $|s_k(x)|=r_k(x)$ es creciente. Similarmente, si $f(x)<0$ se ve que $|s_k(x)|=t_k(x)$ es una sucesión creciente.
Por lo anterior concluimos que $$|s_1|\leq |s_2|\leq |s_3| \leq \dots $$
Si $f$ es acotada, para $N>\sup |f|$ suficientemente grande, tenemos por (1) que para cualquier $x\in X$: $$|f(x)-s_k(x)|\leq |f_+(x)-r_k(x)|+|f_-(x)-t_k(x)|<\frac{1}{2^k}+\frac{1}{2^k}=\frac{1}{2^{k-1}}.$$ Se sigue que en este caso la convergencia es uniforme.
$\square$
Veamos una aplicación del resultado anterior. Como probamos anteriormente [ENLACE], los conjuntos Lebesgue medibles son «casi» Borel medibles. Es entonces esperable que las funciones Lebesgue medibles sean «casi» funciones Borel medibles.
Ejemplo. Sea $f:\mathbb{R}^n\to [-\infty,\infty]$ una función Lebesgue medible. Entonces existe una función $g:\mathbb{R}^n\to[-\infty,\infty]$ Borel medible tal que el conjunto $$\{ x\in \mathbb{R}^n \ | \ f(x)\neq g(x) \}.$$ Es nulo.
Demostración. Supongamos primero que $f\geq 0$. Por el teorema anterior, existe una sucesión $$0\leq s_1\leq s_2\leq \dots$$ De funciones simples $\mathcal{L}$-medibles tales que $$\lim_{k\to \infty} s_k=f.$$
Podemos escribir $$s_k=\sum_{j=1}^{m}\alpha_j^k\chi_{A_j^k}. $$
Donde los $\alpha_j^k\in [0,\infty]$ son distintos dos a dos y los conjuntos $A_j^k$ son ajenos y $\mathcal{L}$-medibles.
Como probamos anteriormente [ENLACE], para cualesquiera $j,k$ admisibles, podemos descomponer $$A_j^k=E_j^k\cup N_j^k$$ Donde $E_j^k\in \mathcal{B}$ y $N_J^K$ es nulo.
Definamos entonces $$\sigma_k=\sum_{j=1}^{m}\alpha_j^k\chi_{E_j^k} $$ Observemos que $\sigma_k$ es una función simple y $\mathcal{B}$ medible para todo $k$. Además, claramente $0\leq \sigma_k\leq s_k$ y $\sigma_k=s_k$ salvo en un conjunto de medida cero $N_k$ (a saber, $N_k=\bigcup_{j=1}^{m}N_j^k$).
Ahora, sean $$N=\bigcup_{k=1}^{\infty}N_k.$$ $$g=\sup_k \sigma_k$$ Notemos que $N$ es nulo. Como $0\leq \sigma_k\leq s_k \leq f$, tomando supremos se tiene $$0\leq g \leq f.$$ Más aún, para cualquier $x\notin N$, se cumple $\sigma_k(x)=s_k(x)$ $\forall k$ $\implies$ $$g(x)=\sup_k \sigma_k(x)=\lim_{k\to \infty} s_k(x)=f(x).$$ Por lo que $f=g$ salvo un conjunto de medida cero ($N$). $g$ es $\mathcal{B}$-medible al ser el supremo de una sucesión de funciones $\mathcal{B}$-medibles. Entonces $g$ es la función buscada.
Consideremos ahora el caso general. Podemos escribir $f=f_+-f_-$. Por lo anterior, existen funciones $\mathcal{B}$ medibles $g_+,g_-$ tales que $0\leq g_+\leq f_+$, $0\leq g_-\leq f_-$ y $f_+=g_+$, $f_-=g_-$ salvo en conjuntos de medida cero. Luego $g=g_+-g_-$ es la función buscada. ($g$ no se «indetermina», pues en los puntos donde $g_+(x)=\infty$, necesariamente $0\leq g_-(x)\leq f_-(x)=0$).
$\square$
Un comentario sobre la generalidad
En la siguiente sección comenzaremos de lleno con teoría de integración sobre $\mathbb{R}^n$. Como lo habíamos adelantado, las funciones $\mathcal{L}$ medibles son las funciones con «la suficiente estructura para ser integradas».
Además de destacar la estructura de la medida de Lebesgue, la razón de que estudiaramos $\sigma$-álgebras y funciones medibles con toda generalidad es que la teoría de integración se puede extender a espacios abstractos de manera inmediata. Como veremos más adelante, basta que exista una función $\mu:\mathcal{M}\to [0,\infty]$ que cumpla propiedades análogas a las de la medida de Lebesgue (una medida general [ENLACE]) para poder definir la integral.
Por simplicidad, nos restringiremos al caso más importante e intuitivo: La integración de funciones $\mathcal{L}$ medibles sobre $\mathbb{R}^n$. La construcción de la integral general es idéntica. Basta reemplazar $(\mathbb{R}^n,\mathcal{L},\lambda)$ por $(X,\mathcal{M},\mu)$ respectivamente en cada una de las definiciones y demostraciones debajo.
Integración de funciones simples
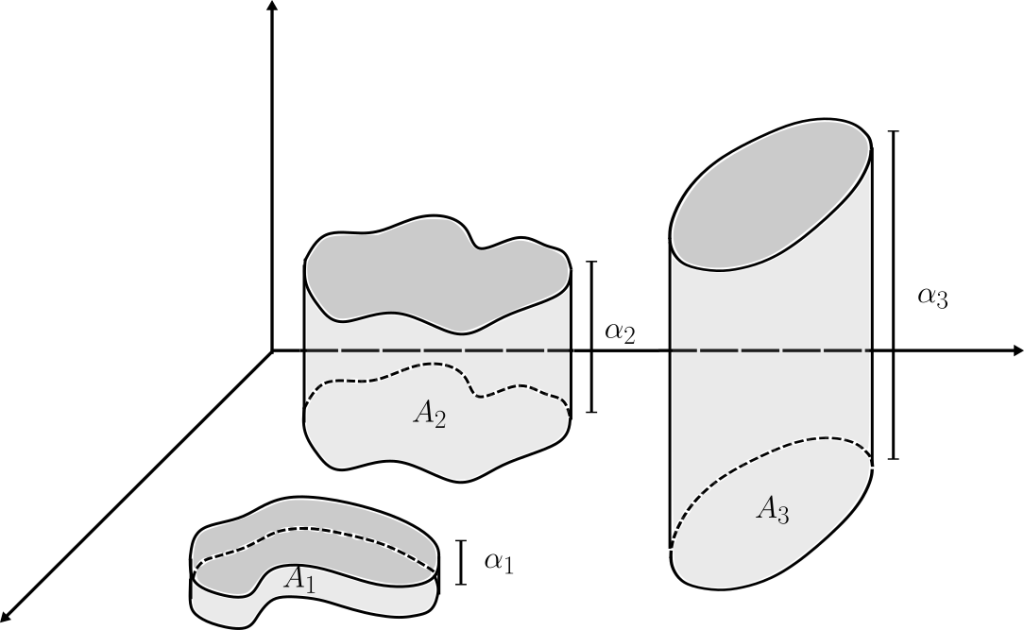
Ya estamos listos para definir la integral de una función simple (y finita) sobre $\mathbb{R}^n$. A manera de motivación, pensemos que $s=\alpha \chi_A$ ($\alpha>0$) es una función (muy) simple en alguna dimensión baja, por ejemplo $\mathbb{R}^2$. Entonces, ¿Cuál es el valor apropiado del «volumen bajo la gráfica» de $s$?. Geométricamente, la región «bajo la gráfica» es un cilindro generalizado con base $A$ y altura $\alpha$ como se observa en la figura. Por analogía con el cálculo de volúmenes de figuras sencillas (o incluso, por analogía con la integral de Riemann), lo más natural es pensar que dicho volúmen debe ser el «área de la base» multiplicado por la «altura». En este caso, por supuesto, podemos interpretar el área de la base como la medida de Lebesgue de $A$, de modo que $$\int s=\alpha\lambda(A).$$
Es la elección más natural para la integral. Similarmente si $s=\sum_{k=1}^{m}\alpha_k\lambda(A_k)$ (con $\alpha_j$ distintos y $A_k$ ajenos), invocando linealidad (o simplemente, «sumando el volúmen de los cilindros por separado») $$\int s=\sum_{k=1}^{m}\alpha_k\lambda(A_k).$$ Es la elección obvia para el valor de la integral.
Definición. Denotaremos por $S_n$ (o simplemente $S$) al conjunto de funciones simples ($\mathcal{L}$) medibles $s$ en $\mathbb{R}^n$ tales que $0\leq s<\infty$.
Dada $s\in S$, podemos expresarla como $$s=\sum_{k=1}^{m}\alpha_k \chi_{A_k},$$ Donde $0\leq \alpha_k<\infty$ y los conjuntos $A_k$ son medibles y ajenos. Entonces, definimos su integral (respecto a la medida de Lebesgue) como: $$\int s \ \mathrm{d}\lambda := \sum_{k=1}^{\infty}\alpha_k\lambda(A_k). $$
Nota. En esta definición, usamos la convención $0\cdot \infty = 0$.
A priori, el valor de la integral podría depender de la representación de $s$ que tomemos (en la definición no pedimos que los $\alpha_k$ sean distintos, así que puede haber una infinidad de representaciones distintas). Aunque como veremos más adelante, la integral está bien definida.
Veamos las primeras propiedades.
Proposición (Propiedades de la integral de una función simple).
- $\int s \ \mathrm{d}\lambda$ está bien definida.
- $0\leq \int s \ \mathrm{d}\lambda \leq \infty.$
- Si $0\leq c <\infty$ es una constante, $\int cs \ \mathrm{d}\lambda=c\int s \ \mathrm{d}\lambda.$
- Si $s,t\in S$, entonces $\int (s+t) \ \mathrm{d}\lambda=\int s \ \mathrm{d}\lambda+\int t \ \mathrm{d}\lambda.$
- Si $s,t\in S$ y $s\leq t$, entonces $\int s \ \mathrm{d}\lambda\leq \int t \ \mathrm{d}\lambda.$
Demostración. Asumiendo 1., los incisos 2. y 3. son inmediatos de la definición.
Probaremos 1. y 5. en el mismo argumento. Supongamos que $s,t\in S$ y $s\leq t$. Tomemos representaciones de $s$ y $t$ de la forma:
\begin{align*}
s &= \sum_{k=1}^{m}\alpha_k\chi_{A_k}, \\
t &= \sum_{j=1}^{l}\beta_j\chi_{B_k}
\end{align*}
Con los $A_k$ y $B_k$ medibles y ajenos dos a dos. Podemos asumir que $\bigcup_{k=1}^{m}A_k=\mathbb{R}^n$ (de no ser así, podemos añadir el término $0\cdot \chi_{A’}$ a la expresión de $s$, donde $A’=\left( \bigcup_{k=1}^{m}A_k \right)^c$, lo que no afecta el valor de la integral bajo esta representación). Similarmente supongamos que $\bigcup_{j=1}^{l}B_j=\mathbb{R}^n$.
Luego, por la aditividad de la medida de Lebesgue y la definición:
\begin{align}
\int s \ \mathrm{d}\lambda &= \sum_{k=1}^{m}\alpha_k\lambda(A_k)=\sum_{k=1}^{m}\sum_{j=1}^{l}\alpha_k\lambda(A_k\cap B_j) \\
\int t \ \mathrm{d}\lambda &= \sum_{j=1}^{l}\beta_j\lambda(B_j)=\sum_{j=1}^{l}\sum_{k=1}^{m}\beta_j\lambda(A_k\cap B_j)
\end{align}
Si $\lambda(A_k\cap B_j)>0$, en particular $A_k\cap B_j\neq 0$, así que podemos tomar un $p\in A_k\cap B_j$. Pero como $s\leq t$: $$\alpha_k=s(p)\leq t(p)=\beta_j.$$
De donde $$\alpha_k\lambda(A_k\cap B_j)\leq \beta_j\lambda(A_k\cap B_j).$$
Si $\lambda(A_k\cap B_j)=0$, es inmediato que $\alpha_k\lambda(A_k\cap B_j)\leq \beta_j\lambda(A_k\cap B_j)$. Comparando (2) y (3) término a término conluimos que: $$\int s \ \mathrm{d}\lambda\leq \int t \ \mathrm{d}\lambda.$$ (Al tomar cualesquiera representaciones válidas de $s$ y $t$). Esto demuestra 5. pero también demuestra 1:
Si tomamos dos representaciones distintas de $s$, la desigualdad $s\leq s$ implica desigualdades simétricas sobre las integrales definidas por las distintas representaciones, lo que garantiza su igualdad.
Ahora veamos 4. Usando la misma notación que en el inciso anterior podemos escribir:
$$s+t=\sum_{k=1}^{m} \sum_{j=1}^{l}(\alpha_k+\beta_j)\chi_{A_k\cap B_j}.$$
Luego:
\begin{align*}
\int (s+t) \ \mathrm{d}\lambda &= \sum_{k=1}^{m} \sum_{j=1}^{l}(\alpha_k+\beta_j)\lambda(A_k\cap B_j) \\
&= \sum_{k=1}^{m} \sum_{j=1}^{l} \alpha_k\lambda(A_k\cap B_j) + \sum_{k=1}^{m} \sum_{j=1}^{l} \beta_j\lambda(A_k\cap B_j) \\
&= \int s \ \mathrm{d}\lambda + \int t \ \mathrm{d}\lambda.
\end{align*}
$\square$
Más adelante…
Definiremos la integral de una función medible y no negativa en general, usando fuertemente las ideas de aproximación por funciones simples y las propiedades de la integral de funciones simples.