Introducción

El contenido de esta sección corresponde al libro
Wheeden, R.L., Zygmund, A., Measure and Integral. An Introduccion to Real Analysis. (2da ed.). New York: Marcel Dekker, 2015, págs 17-22.

Estamos por presentar las últimas notas de blog del curso de Análisis Matemático I. Pretendemos mostrar un puente entre lo que vimos aquí y lo que se aprenderá en Análisis Matemático II. Conoceremos algunas ideas que, eventualmente, nos llevarán al concepto de la integral de Riemann-Stieljes, un concepto que generaliza a la integral de Riemann (que suele verse en los cursos de Cálculo) pero que también es un caso particular de la integral de Lebesgue, la que se verá en la siguiente sección del blog. Para comenzar, analicemos los cambios que una función va tomando en un dominio cerrado.

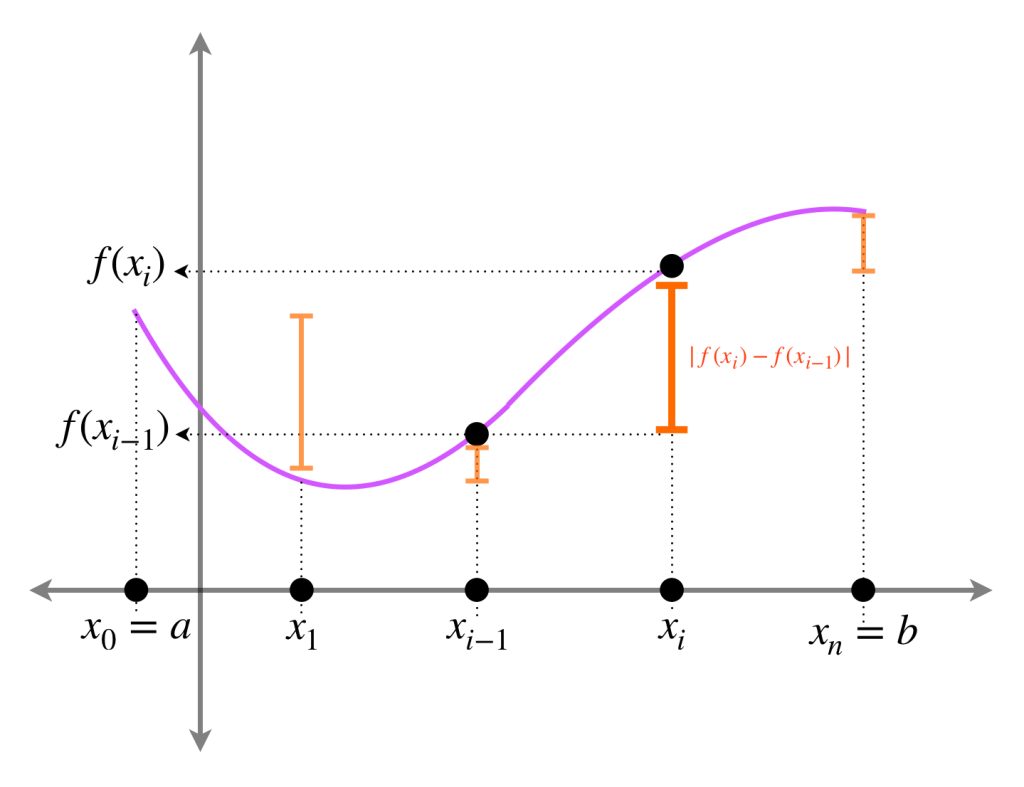
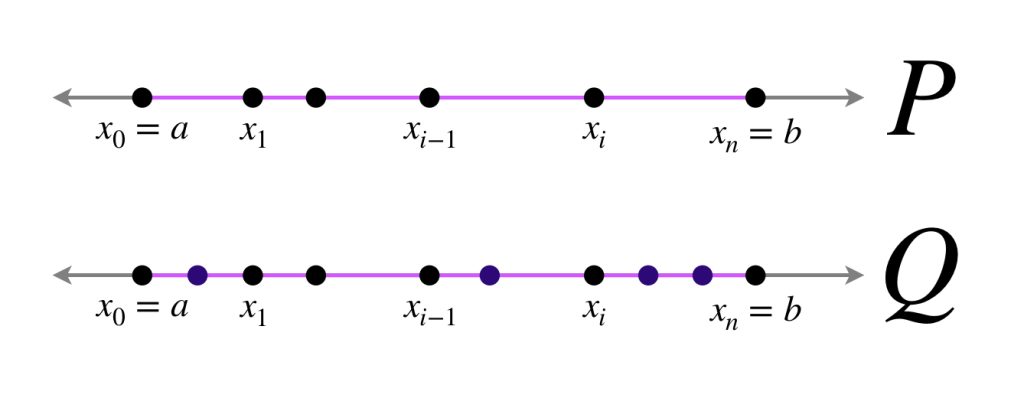
Definición. Partición de un intervalo $\textbf{[a,b].}$ Sea $[a,b]$ un intervalo de $\mathbb{R}.$ Si $P = \{x_0=a, \, x_1, \, x_2,…,x_{n-1}, \, x_n = b\}, \, i=0,1,2,…,n \,$ es una colección de puntos tales que $x_0 =a, \, x_n = b$ y para cada $i =1,2,…,n$ se cumple que $x_{i-1}< x_i,$ entonces diremos que $P$ es una partición de $[a,b].$

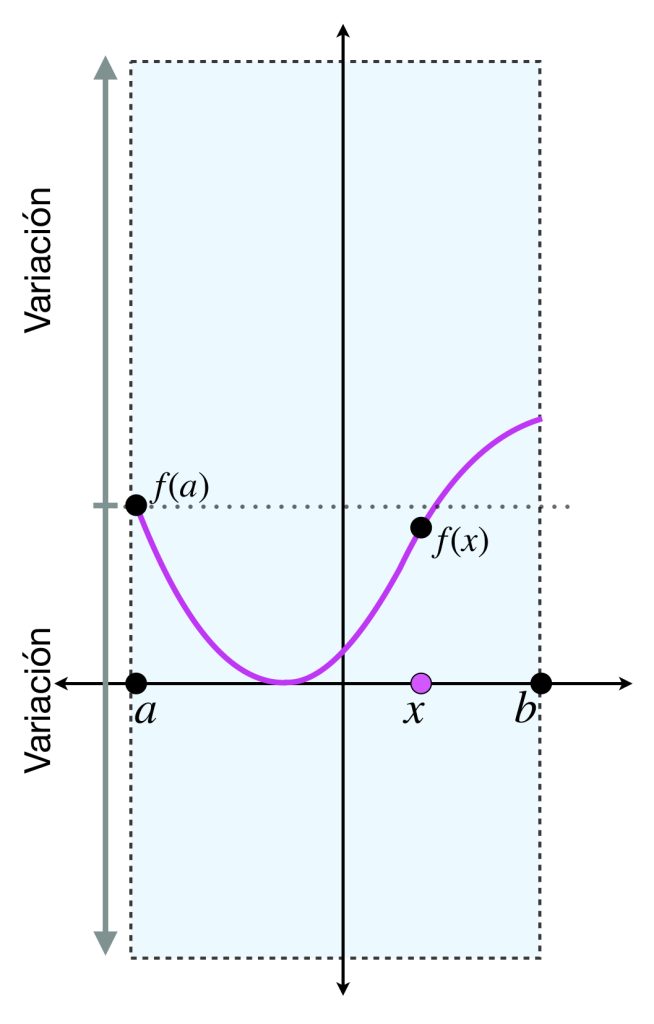
Definición. Variación de $f$ sobre $[a,b].$ Considera una función $f:[a,b] \subset \mathbb{R} \to \mathbb{R} \,$ y sea $P=\{x_0, \, x_1, \, …, \, , x_n\}$ una partición de $[a,b].$ Definimos $S_P[f;a,b]$ (o bien $S_P$ cuando no hay necesidad de especificar la función y el intervalo) como:
$$S_P[f;a,b] := \sum_{i=1}^{n}|f(x_i) \, -\, f(x_{i-1})|$$

Entonces se suman las distancias que se generan al evaluar $f$ en cualesquiera dos puntos consecutivos de la partición.

Ya que para cada partición $P$ de $[a,b]$ existe su respectiva $S_P,$ podemos pensar en si la colección de todas las sumas tiene supremo. El supremo de las sumas de todas las particiones de $[a,b]$ recibe el nombre de variación de $f$ sobre $[a,b].$ Se denota como:
$$ \underset{P \, \in \, \mathcal{P_{[a,b]}}}{Sup} \, S_P \, =V[f;a,b] \, = V [a,b]\, = V$$

Donde $\mathcal{P}_{[a,b]} \,$ es el conjunto de particiones de $[a,b].$

Definición. Función de variación acotada y de variación no acotada. Sea $f:[a,b] \to \mathbb{R}.$ Considera $V[f;a,b].$ Si el supremo de hecho existe en $\mathbb{R},$ entonces $0 \leq V$ y diremos que $f$ es de variación acotada en $[a,b].$
En otro caso diremos que $V = \infty \,$ y que $f$ es de variación no acotada.

Ejemplos de variación en funciones

A continuación presentamos las variaciones de algunas funciones. Al final de esta sección te pediremos calcular los resultados formalmente.

Las siguientes son propiedades de las funciones de variación acotada.

Proposición. Si $f$ es de variación acotada en $[a,b]$ entonces $f$ es acotada en $[a,b].$

Demostración:
Sea $x \in [a,b].$ Considera la partición $\{a, \, x, \, b\},$ entonces
$$|f(x) \, – \, f(a)| \leq |f(x) \, – \, f(a)| +|f(b) \, – \, f(x)| \leq V.$$
Por lo tanto, $f$ es acotada en $[a,b].$

El regreso no es cierto, esto es, podemos tener una función acotada en $[a,b]$ pero que no sea de variación acotada. La función de Dirichlet ejemplifica esta situación. Podrás ver otro caso también en la tarea moral de la siguiente entrada).

Proposición. Sean $f,g \,$ funciones de variación acotada en $[a,b]$ y sea $c \in \mathbb{R}.$ Entonces las funciones

• $cf,$
• $f+g \,$ y
• $fg$

son de variación acotada en $[a,b].$ Además

• $\dfrac{f}{g}$

también es de variación acotada en $[a,b]$ si para todo $x \in [a,b]$ existe $\varepsilon >0$ tal que $|g(x)| \geq \varepsilon.$ La demostración queda como ejercicio.

Con las siguientes ideas tendremos recursos para aproximar mejor el valor de $V$ de una función.

Definición. Refinamiento. Sean $P,Q \in \mathcal{P}_{[a,b]} \,$ tales que $P \subseteq Q,$ es decir, $Q$ tiene todos los puntos de $P$ y, posiblemente, algunos otros. Entonces decimos que $Q$ es un refinamiento de $P,$ o que $Q$ refina a $P.$

Proposición: Si $Q$ es un refinamiento de $P,$ entonces $S_P \leq S_Q.$ La demostración la dejamos como ejercicio.

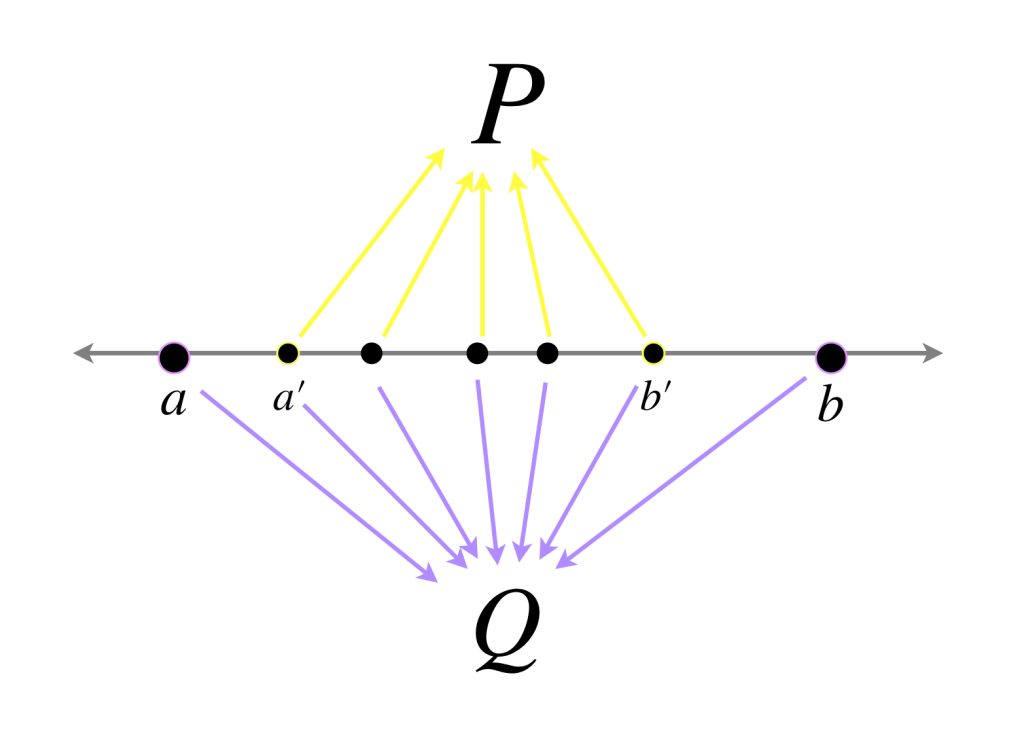
Proposición: Sea $f:[a,b] \to \mathbb{R}.$ Si $[a’,b’] \subseteq [a,b]$ entonces $V[a’,b’] \leq V[a,b],$ es decir, la variación potencialmente incrementa con el intervalo.

Demostración:
Sea $P= \{x_0= a’,…,x_n=b’\} \,$ una partición de $[a’,b’]$ y sea $Q = P \cup \{a,b\}.$ Claramente, $Q$ es partición de $[a,b]$ y
\begin{align*}
S_P[f;a’,b’] &= \sum_{i=1}^{n}|f(x_i) \, -\, f(x_{i-1})|\\
&\leq \sum_{i=1}^{n}|f(x_i) \, -\, f(x_{i-1})|+|f(x_0) \, -\, f(a)|+|f(b) \, -\, f(x_{n})|\\
&= S_Q[f;a,b]
\end{align*}

lo cual indica que para cada $S_P, \, P \in \mathcal{P}_{[a’,b’]}$ existe $S_Q, \, Q \in \mathcal{P}_{[a,b]}$ tal que $S_P \leq S_Q.$ Por lo tanto $V[a’,b’] \leq V[a,b].$

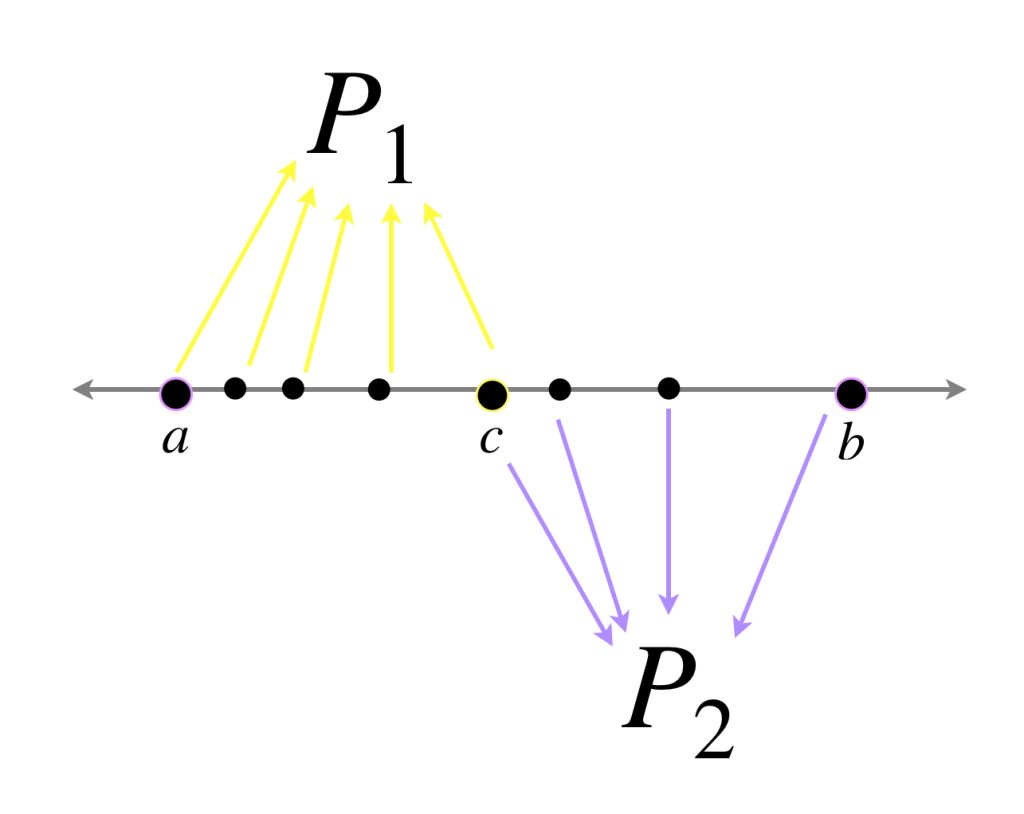
Proposición: Sea $f:[a,b] \to \mathbb{R}.$ Si $a < c < b$ entonces
$$V[a,b] = V[a,c] + V[c,b].$$
Es decir, la variación es aditiva en intervalos adyacentes.

Demostración:
Probemos primero que $V[a,c] + V[c,b] \leq V[a,b].$ Sea $P_1$ y $P_2$ particiones de $[a,c]$ y $[c,b],$ respectivamente. Entonces $P = P_1 \cup P_2$ es una partición de $[a,b].$

En consecuencia
$$S_{P_1}[f,a,c]+S_{P_2}[f,c,b] = S_P[f,a,b].$$
Ya que aún podrían existir otros valores más grandes de $S_{P’}[f,a,b]$ con $P’$ partición de $[a,b],$ se sigue que $V[a,c] + V[c,b] \leq V[a,b].$

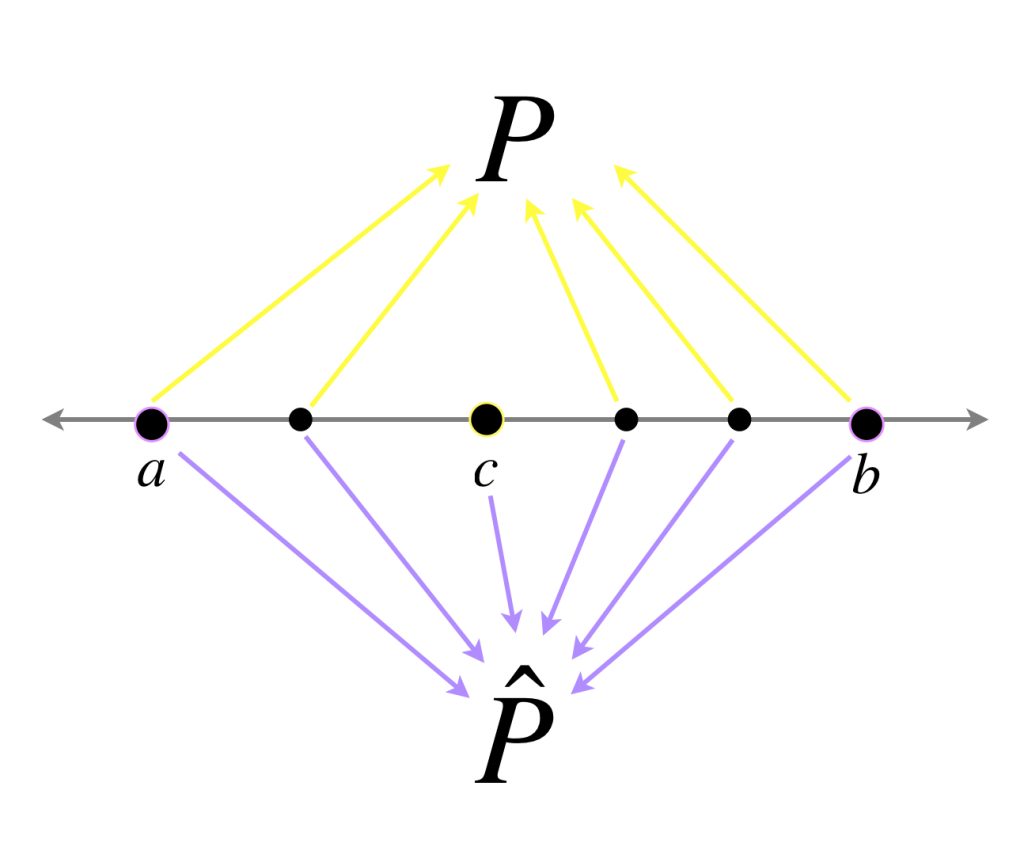
Ahora probemos que $V[a,b] \leq V[a,c] + V[c,b].$ Sea $P$ una partición de $[a,b]$ y $\hat{P}= P \cup \{c\}.$

Entonces $\hat{P}$ es un refinamiento de $P,$ y por la proposición que dejamos al lector tenemos
$$S_P[f,a,b] \leq S_{\hat{P}}[f,a,b] = S_{P_1}[f,a,c]+S_{P_2}[f,c,b]$$
por lo tanto $V[a,b] \leq V[a,c] + V[c,b],$ con lo que concluimos que

$$V[a,b] = V[a,c] + V[c,b].$$

Definición. Partes positiva y negativa de $x$. Para cualquier $x \in \mathbb{R}$ definimos la parte positiva de $x$ como:

\begin{equation*}
x^+ = \begin{cases}
x & \text{si $x >0$} \\
0 & \text{si $x \leq 0$}
\end{cases}
\end{equation*}

Y la parte negativa de $x$ como:

\begin{equation*}
x^- = \begin{cases}
0 & \text{si $x >0$} \\
-x & \text{si $x \leq 0$}
\end{cases}
\end{equation*}

Nota que las partes positiva y negativa de un número real, satisfacen las siguientes relaciones:

1. $x^+,x^- \geq 0.$
2. $|x|=x^++x^- .$
3. $x = x^+-x^- .$

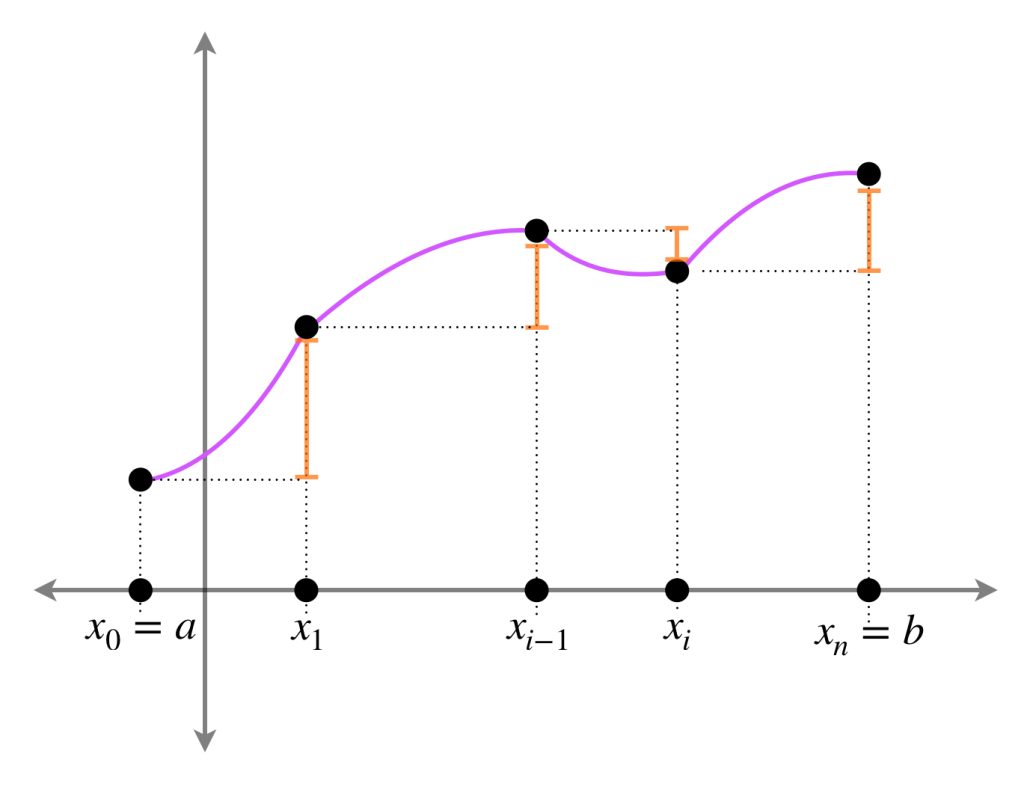
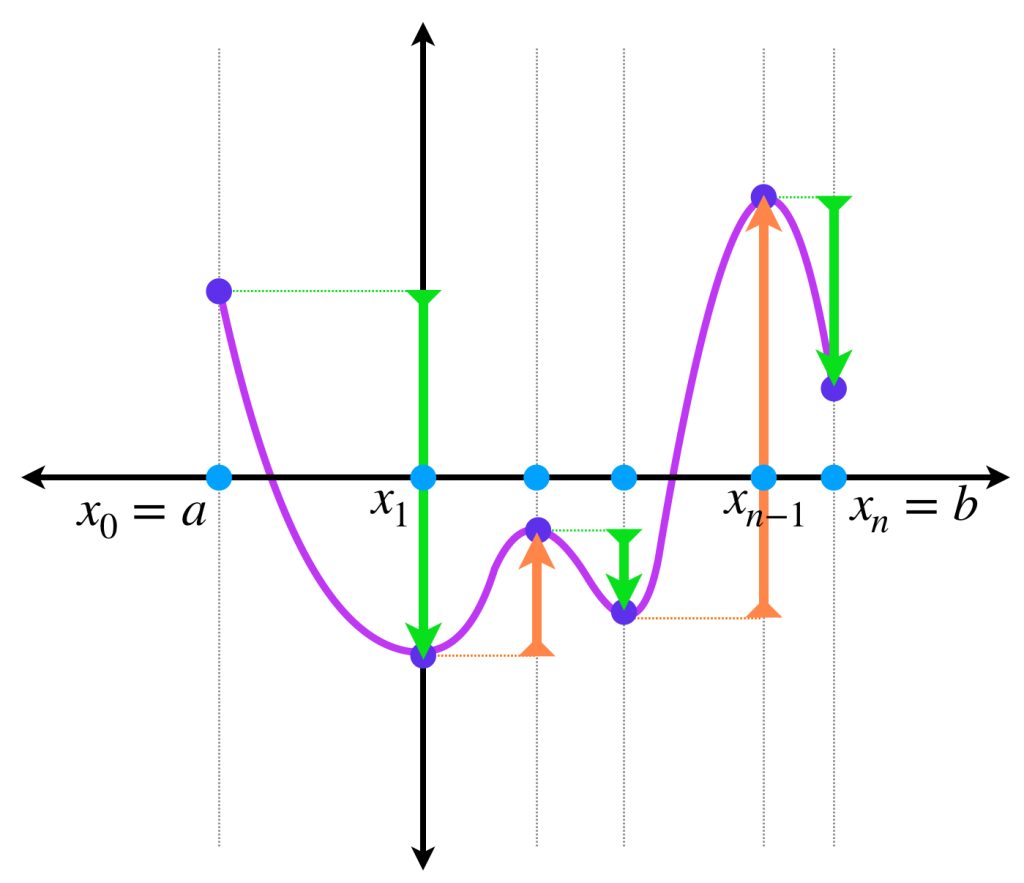
Definición. Suma de términos positivos y suma de términos negativos de $S_P.$ Sea $f:[a,b] \to \mathbb{R} \,$ y $P=\{x_0, \, x_1, \, … \, , x_{n-1}, \, x_n\}.$ Definimos la suma de términos positivos de $S_P$ como:

$$S_P^+=S_P^+[f;a,b]= \sum_{i =1}^{n} \, (f(x_i)-f(x_{i-1}))^+.$$

Y la suma de términos negativos de $S_P$ como:

$$S_P^-=S_P^-[f;a,b]= \sum_{i =1}^{n} \, (f(x_i)-f(x_{i-1}))^-.$$

En la siguiente imagen, las líneas naranjas representan los sumandos distintos de cero en $S_P^+$ y las líneas verdes, los de $S_P^-.$

Es sencillo comprobar que

\begin{align}
S_P^+ + S_P^- &= S_P \, \, \, \text{ y } \\
S_P^+ \, – \, S_P^- &=f(b) – f(a).
\end{align}

Definición: Variación positiva y variación negativa de $f.$ Definimos la variación positiva de $f$ como:

$$S^+=S^+[f;a,b]= \underset{P \in \mathcal{P}}{Sup \, } \, S_P^+$$

Y la variación negativa de $f$ como:

$$S^-=S^-[f;a,b]= \underset{P \in \mathcal{P}}{Sup \,} \, S_P^-$$

Nota que ambas son mayores iguales que cero y pueden valer $\infty$ cuando no existe el supremo en $\mathbb{R}$.

Proposición. Si alguno de $S^+, \, S^-, \, $ o $V$ es finito entonces los tres son finitos. Más aún, se satisface:

\begin{align}
S^++S^- &=V, \\
S^+-S^- &= f(b)-f(a)
\end{align}

o equivalentemente

\begin{align}
S^+&= \frac{1}{2}[V+f(b)-f(a)], \\
S^-&= \frac{1}{2}[V-f(b)+f(a)]
\end{align}

Demostración:
Supongamos que $V$ es finito. Por (1)
$$S_P^+ + S_P^- = S_P$$
y como $S_P \leq V,$ se sigue que
\begin{align*}
S_P^+ + S_P^- \leq V.
\end{align*}

Ya que tanto $S_P^+$ como $S_P^- $ son no negativos, tenemos
$$S_P^+ \leq V \, \Rightarrow \, S^+ \leq V.$$
De igual manera
$$S_P^- \leq V \, \Rightarrow \, S^- \leq V.$$

Por lo tanto, si $V$ es finito, $S^+$ y $S^-$ también lo son.

Ahora supongamos que $S^+$ es finito. Despejando en (2), se cumple:

\begin{align*}
&& S_P^- &= S_P^+ – \, (f(b) \, – \, f(a))\\
& \Rightarrow & &\leq S^+ – \, (f(b) \, – \, f(a))\\
\end{align*}

De modo que el conjunto de sumas de términos negativos está acotado y por lo tanto $S^-$ también es finito.

Por (1)
\begin{align}
\nonumber && S_P = S_P^+ + S_P^- &\leq S^+ + S^- \\
&\Rightarrow& V &\leq S^+ + S^-
\end{align}

En consecuencia, $V$ es finito.
Análogamente, podemos concluir que si $S^-$ es finito, $S^+$ y $V$ son finitos.

Para probar (4) considera una sucesión de particiones $(P_n)_{n \in \mathbb{N}}$ tal que la sucesión de sumas positivas cumple que

$$(S_{P_n}^+) \, \to \, S^+.$$

Vamos a demostrar que también $(S_{P_n}^-) \, \to \, S^-$ y que $S^+ \, – \, (f(b)\, – \, f(a)) = S^-,$ que es equivalente a (4).

Por (2) tenemos que $S_{P_n}^- = S_{P_n}^+- \, (f(b) \, – \, f(a)) ,$
y como $(S_{P_n}^+) \, \to \, S^+$
entonces $S_{P_n}^+- \, (f(b) \, – \, f(a)) \, \to \, S^ + -\, (f(b) \, – \, f(a)),$
y por transitividad
\begin{align}
S_{P_n}^- \, \to \, S^ + -\, (f(b) \, – \, f(a)).
\end{align}

Dado que $S_{P_n}^ – \leq S^ -,$ se sigue
\begin{align}
S^ + – \, (f(b) \, – \, f(a)) \leq S ^-.
\end{align}

Queremos que se cumpla la igualdad. Supón por el contrario que

$$S^ + – \, (f(b) \, – \, f(a)) < S ^-,$$

como $S ^-$ es el supremo de las sumas negativas, existe una partición $P$ de $[a,b]$ tal que

\begin{align}
&&S^ + – \, (f(b) \, – \, f(a))&<S_P ^- \\
&\Rightarrow& S^ + &<S_P ^- + (f(b) \, – \, f(a)) \\
&& &= S_P^+
\end{align}

lo cual es una contradicción, pues $S ^+$ es el supremo de las sumas positivas. Por lo tanto

\begin{align}
S^ + – \, (f(b) \, – \, f(a)) = S ^-,
\end{align}

Lo que prueba (4),

y por (8)
\begin{align}
S_{P_n} ^- \, \to \, S ^-,
\end{align}

Por otro lado, por (1)
$$S_{P_n}^+ + S_{P_n}^- = S_P \leq V$$
de modo que tomando el límite
\begin{align}
S^+ + S^- \leq V
\end{align}

y de (7) y (15) concluimos finalmente

$$S^+ + S^- = V$$

que es (3).

Finalizamos esta sección con el siguiente

Corolario. Teorema de Jordan. Una función $f:[a,b] \to \mathbb{R}$ es de variación acotada en $[a,b]$ si y solo si puede ser expresada como la diferencia de dos funciones crecientes acotadas en $[a,b].$

Demostración:
Supón que $f$ es de variación acotada. Por un resultado visto arriba, sabemos que $f$ es de variación acotada en cada subintervalo $[a,x]$ con $x \in [a,b].$ Para cada $x,$ sean $S(x) ^+$ y $S(x) ^-$ las variaciones positiva y negativa de $f$ en $[a,x].$ Es sencillo demostrar que estas funciones son crecientes y acotadas en $[a,b],$ (ver tarea moral), y aplicando el teorema anterior en cada $[a,x],$
\begin{align*}
&& S(x) ^+ \, – \, S(x) ^- &= f(x) \, – \, f(a) \\
&\Rightarrow&f(x) &= (S(x) ^+ +f(a)) \, – \, S(x) ^-
\end{align*}

Como $S(x)$ es creciente y acotada, también lo es $(S(x) ^+ +f(a))$, de modo que $f$ es la diferencia de dos funciones crecientes y acotadas.

En contraparte, supongamos que $f = f_1 \, – \, f_2,$ donde $f_1$ y $f_2$ son funciones crecientes y acotadas en $[a,b].$ De acuerdo con el primer ejemplo, ambas funciones son de variación acotada. Finalmente, por un resultado enunciado arriba, $ f_1 \, – \, f_2 = f \,$ es de variación acotada.

Más adelante…

Seguiremos con el estudio de las funciones de variación acotada y conectaremos con curvas rectificables, una concepción de cómo considerar la longitud de una curva que podría no coincidir, con medir la gráfica de la misma.

Tarea moral

1. Verifica la variación de cada función de los ejemplos enunciados arriba.
2. Demuestra que si $f,g \,$ son funciones de variación acotada en $[a,b]$ y $c \in \mathbb{R},$ entonces las funciones
   $$cf, \, f+g \, \, \text{ y } \, \, fg$$
   son de variación acotada en $[a,b].$ Además
   $$\frac{f}{g}$$
   también es de variación acotada en $[a,b]$ si para todo $x \in [a,b]$ existe $\varepsilon >0$ tal que $|g(x)| \geq \varepsilon.$
3. Prueba que si $Q$ es un refinamiento de $P,$ entonces $S_P \leq S_Q.$
4. Para cada $x,$ sean $S(x) ^+$ y $S(x) ^-$ las variaciones positiva y negativa de $f$ en $[a,x].$ Demuestra que estas funciones son crecientes y acotadas en $[a,b].$
5. Prueba que si $f:[a,b] \to \mathbb{R}$ es Lipschitz continua, entonces es de variación acotada.

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.