Sea $ f : U \subseteq \mathbb{R}^2 \rightarrow \mathbb{R}$ , diferneciable en un abierto, convexo $ U. $
Sea $ (x_0, y_0) \in U$ y $ (h, k) $ cercano a $ (x_0, y_0) $, tal que $(x_0 + h , y_0 + k) \in U.$
Como $ U $ es convexo, entonces $$ (1 \, – \,t) (x_0, y_0) + t ( x_0 + h , y_0 + k) = (x_0 + t h , y_0 + t k) \in U$$
Podemos parametrizar el segmento de recta $ \alpha (t) = (x_0 + t h, y_0 + t k) $ y hacer la composición $ f \, \circ \, \alpha : [ 0, 1] \rightarrow \mathbb{R}$
Le podemos aplicar:
(*) el teorema del valor medio para funciones de $\mathbb{R} \rightarrow \mathbb{R}$, y también
(*) la regla de la cadena.
${}$
Teorema del valor medio para derivadas
Si $ g $ es continua en el cerrado $[0, 1]$ y derivable en el abierto $(0, 1)$, entonces existe $\theta \in (0, 1) $ tal que
$$g’ (\theta) = \dfrac{g (1) \, – \, g (0) }{1 \, – \, 0} = g (1) \, – \, g (0) $$
donde $ g = f \, \circ \, \alpha$
$ ( f \, \circ \, \alpha ) (\theta) = \nabla f ( \alpha ( \theta )) \cdot {\alpha}’ (\theta) = \dfrac{\partial f}{\partial x} (x_0 + \theta h , y_0 + \theta k) h \, + \, \dfrac{\partial f}{\partial y} (x_0 + \theta h , y_0 + \theta k) k$
Sabemos que
$ f (x_0 + h , y_0 + k) = f (x_0 , y_0) + \nabla f ( \alpha ( \theta )) \cdot {\alpha}’ (\theta) $
$ f (x_0 + h , y_0 + k) \, – \, f (x_0 , y_0) = \nabla f ( \alpha ( \theta )) \cdot {\alpha}’ (\theta) $
Si $ f $ fuera de clase $\mathcal{C}^2$ podríamos decir más, en particular $ g = f \, \circ \, \alpha \in \mathcal{C}^2$
$g (t) = f ( x_0 + t h, y_0 + t k)$
$g’ (t) = \dfrac{\partial f}{\partial x} ( x_0 + t h, y_0 + t k) h \, + \, \dfrac{\partial f}{\partial y} ( x_0 + t h, y_0 + t k) k$
Queremos calcular $ {g}^{\prime \prime} (t)$.
Examinemos $\dfrac{\partial f}{\partial x} ( x_0 + t h, y_0 + t k) = G ( x_0 + t h, y_0 + t k)$
Sea $G (x, y) = \dfrac{\partial f}{\partial x} (x, y)$, entonces
$ \dfrac{d}{dt} G ( x_0 + t h, y_0 + t k) = \dfrac{\partial G}{\partial x} ( x_0 + t h, y_0 + t k) h \, + \, \dfrac{\partial G}{\partial y}( x_0 + t h, y_0 + t k) k$
Entonces
$$ {g}^{\prime \prime} (t) = \Bigg( \dfrac{\partial^2 f}{\partial x^2} ( x_0 + t h, y_0 + t k) h \, + \, \dfrac{\partial f}{\partial y \partial x} ( x_0 + t h, y_0 + t k) k \Bigg) h \, + \, \Bigg( \dfrac{\partial f}{\partial x \partial y} ( x_0 + t h, y_0 + t k) h \, + \, \dfrac{\partial^2 f}{\partial y^2} ( x_0 + t h, y_0 + t k) k \Bigg) k$$
$${g}^{\prime \prime}(t) = \dfrac{\partial^2 f}{\partial x^2} ( x_0 + t h, y_0 + t k) h^2 \, + \, 2 \dfrac{\partial^2 f}{\partial y \partial x} ( x_0 + t h, y_0 + t k) h k \, + \, \dfrac{\partial^2 f}{\partial y^2} ( x_0 + t h, y_0 + t k) k^2 $$
${g}^{\prime \prime}(t) $ es la segunda derivada de $ ( f \, o \, \alpha) ( t ).$
La tercera derivada de $ f ( \alpha ( t ) )$ es $$ \dfrac{\partial^3 f}{\partial x^3} h^3 \, + \, 3 \dfrac{\partial^3 f}{\partial x^2 \partial y} h^2 k \, + \, 3 \dfrac{\partial^3 f}{\partial x \partial y^2} h k^2 \, + \, \dfrac{\partial^3 f}{\partial y^3} k^3 $$ valuada en $( x_0 + t h, y_0 + t k)$
${}$
Teorema de Taylor para funciones de $\mathbb{R} \rightarrow \mathbb{R}$ aplicado a $ g = f \, \circ \, \alpha$
$g ( t ) = g ( 0 ) + g’ ( 0 ) t + \frac{1}{2} {g}^{\prime \prime} ( 0 ) t^2 + E ( t )$ , donde $ E ( t )$ es el error.
Una fórmula para este error es $ \dfrac{{g}^{\prime \prime \prime} ( \xi ) }{ 3! } $ para alguna $ \xi \in ( 0, t)$
Entonces
$ g ( t ) = f ( x_0 + t h, y_0 + t k)$
$ g ( 0 ) = f ( x_0 , y_0 )$
$ g’ ( 0 ) = \dfrac{\partial f}{\partial x} ( x_0 , y_0 ) h + \dfrac{\partial f}{\partial y} ( x_0 , y_0 ) k$
$ {g}^{\prime \prime} ( 0 ) = \dfrac{\partial^2 f}{\partial x} ( x_0 , y_0 ) h^2 + 2 \dfrac{\partial^2 f}{\partial y \partial x} ( x_0 , y_0 ) h k + \dfrac{\partial^2 f}{\partial y^2} ( x_0 , y_0 ) k^2 $
$ \dfrac{{g}^{\prime \prime \prime} ( \xi)}{3!} = \dfrac{\dfrac{\partial^3 f}{\partial x^3} (x_0 + \xi h, y_0 + \xi k ) h^3 \, + \, 3 \dfrac{\partial^3 f}{\partial x^2 \partial y} (x_0 + \xi h, y_0 + \xi k ) h^2 k \, + \, 3 \dfrac{\partial^3 f}{\partial x \partial y^2} (x_0 + \xi h, y_0 + \xi k ) h k^2 \, + \, \dfrac{\partial^3 f}{\partial y^3} (x_0 + \xi h, y_0 + \xi k )}{3!} $
Si $f $ es de clase $\mathcal{C}^3$ ya tenemos un polinomio de 2° grado que aproxima bien a $f$ localmente.
Si el punto es un $\textit{ punto crítico }$ entonces, el polinomio de 2° grado es, esencialmente, un polinomio homogéneo.
$ p (x, y) = ax^2 + 2bxy + cy^2 $
$ p ( 0, 0 ) = 0$
El vector gradiente $ \nabla p ( 0, 0) = \Big( \dfrac{\partial p }{\partial x} , \dfrac{\partial p }{\partial y} \Big) \Biggm|_{(0, 0)} = ( 2ax + 2 by, 2 bx + 2 cy ) \Biggm|_{(0, 0)} = (0, 0)$
El plano tangente a $ z = p (x, y )$ en el origen es horizontal.
Observación:
La matriz $ A = \begin{equation*} \begin{pmatrix} a & b \\ b & c \end{pmatrix} \end{equation*}$ es simétrica.
También sabemos que si la matriz es diagonalizable, entonces existe una base ortonormal de vectores propios $\vec{v_1}, \, \vec{v_2}$ tales que
$\| \vec{v_1} \| = \| \vec{v_2} \| = 1$ y también $ \vec{v_1} \cdot \vec{v_2} = 0$
Y existe $\theta$ tal que
$ \vec{v_1} = (\cos \theta , \sin \theta ) $
$ \vec{v_2} = (\, – \ \sin \theta, \cos \theta) $
Además, existen $\lambda_1 , \, \lambda_2$ tales que $$ A \vec{v_1} = \lambda_1 \vec{v_1} $$ $$ A \vec{v_2} = \lambda_2 \vec{v_2} $$
$D = \begin{equation*} \begin{pmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{pmatrix} \end{equation*}$ es la matriz diagonal.
Sin pérdida de generalidad en al caso cuando
$\begin{equation*} \begin{pmatrix} a & b \\ b & c \end{pmatrix} = \begin{pmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{pmatrix} \end{equation*}$
$ p (x, y) = \lambda_1 x^2 + \lambda_2 y^2$
Analicemos los tres casos posibles según los valores de $\lambda$
CASO 1: $ \lambda_1 , \lambda_2 > 0$ entonces, $p$ alcanza un valor mínimo.
https://www.geogebra.org/classic/drtwmcwt
Ejemplo: $p (x, y) = x^2 + y^2 $
CASO 2: $ \lambda_1 , \lambda_2 < 0$ entonces, $p$ alcanza un valor máximo.
https://www.geogebra.org/classic/zkkwuga4
Ejemplo: $p (x, y) = \, – \, x^2 \, – \, y^2 $
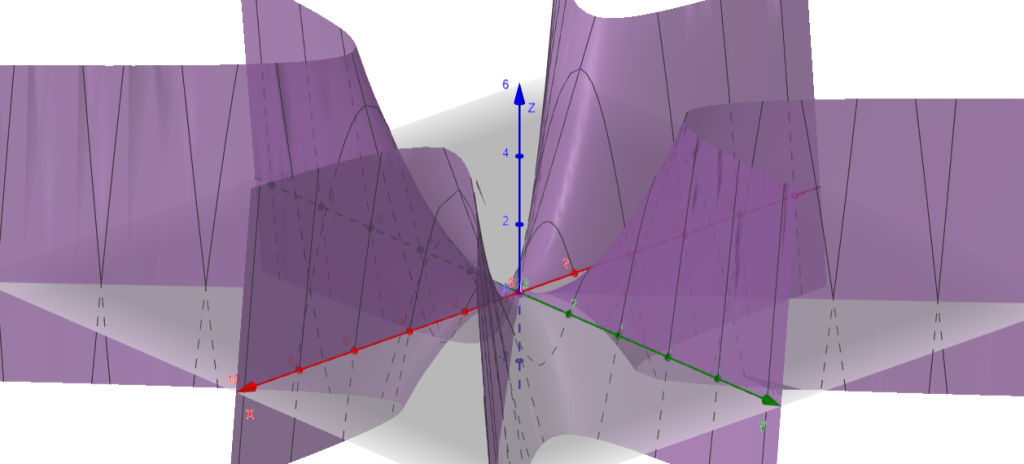
CASO 3: $ \lambda_1 > 0 , \lambda_2 < 0$ entonces, $p$ tiene un punto silla.
https://www.geogebra.org/classic/yczbtnvb
Ejemplo: $p (x, y) = x^2 \, – \, y^2 $
Si alguno de los $\lambda$ es CERO, no se puede concluir nada acerca del punto.
${}$
$\underline{\textit{Veamos un ejemplo}}:$
$p (x, y) = 2xy$
Como $ p (x, y) = ax^2 + 2bxy + cy^2$ entonces, para nuestro ejemplo tenemos que:
$ a = 0$ , $ b = 1$ , y $ c = 0$.
Entonces la matriz $A = \begin{equation*} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \end{equation*}$
Entonces $\begin{equation*} \begin{vmatrix} – \, \lambda & 1 \\ 1 & – \, \lambda \end{vmatrix} \end{equation*} = 0$
$ \lambda^2 \, – \, 1 = 0 $
$ \lambda^2 = 1$ y por tanto $ \lambda = \pm 1$
$\underline{\textit{Vectores propios}}:$
$$\begin{equation*} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = 1 \begin{pmatrix} x \\ y \end{pmatrix} \end{equation*}$$
Entonces
$$\begin{equation*} \begin{pmatrix} y \\ x \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} \end{equation*}$$
Luego $ \vec{v_1} = \dfrac{( 1, 1)}{ \| \vec{v_1} \|} = \begin{pmatrix} \dfrac{1}{\sqrt{2}} \\ {} \\ \dfrac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} \cos \dfrac{\pi}{4} \\ {} \\ \sin \dfrac{\pi}{4} \end{pmatrix}$
Análogamente,
$$\begin{equation*} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \, – \, 1 \begin{pmatrix} x \\ y \end{pmatrix} \end{equation*}$$
Entonces
$$\begin{equation*} \begin{pmatrix} y \\ x \end{pmatrix} = \begin{pmatrix} \, – \, x \\ \, – \, y \end{pmatrix} \end{equation*}$$
Luego $ \vec{v_2} = \begin{pmatrix} \dfrac{ \, – \, 1}{\sqrt{2}} \\ {} \\ \dfrac{ \, – \, 1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} \, – \, \sin \dfrac{\pi}{4} \\ {} \\ \cos \dfrac{\pi}{4} \end{pmatrix}$
${}$
Corte con el plano vertical $ x = y$ son las parábolas $p (x, y) = 2x^2$
Corte con el plano vertical $ y = \, – \, x$ son las parábolas $p (x, y) = \, – \, 2x^2$