MATERIAL EN REVISIÓN
Introducción
Estamos en condiciones de enunciar y demostrar otro de los teoremas más importantes en la teoría de integración de Lebesgue: El teorema de la convergnecia Dominada. Éste nos garantiza condiciones «relativamente débiles» bajo las cuales podemos intercambiar límites e integrales. La gracia de este teorema es que aplica para funciones medibles de todo tipo (no necesariamente positivas o crecientes) siempre que podamos encontrar alguna función en $L^1$ que «domine» en valor absoluto a todas las demás.
Teorema de la convergencia dominada. Sea $f_1,f_2,f_3,\dots$ una sucesión de funciones medibles en $\mathbb{R}^n$ tales que : $$\lim_{k\to \infty}f_k(x)$$ Existe para todo $x\in \mathbb{R}^n$, y existe una función $g\in L^1$ tal que \begin{equation}|f_k(x)|\leq g(x) \end{equation} Para todo $x\in \mathbb{R}^n$ y $k\in \mathbb{N}$. Entonces $f\in L^1$ y $$\int \left( \lim_{k\to \infty} f_k \right) \ \mathrm{d} \lambda = \lim_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$
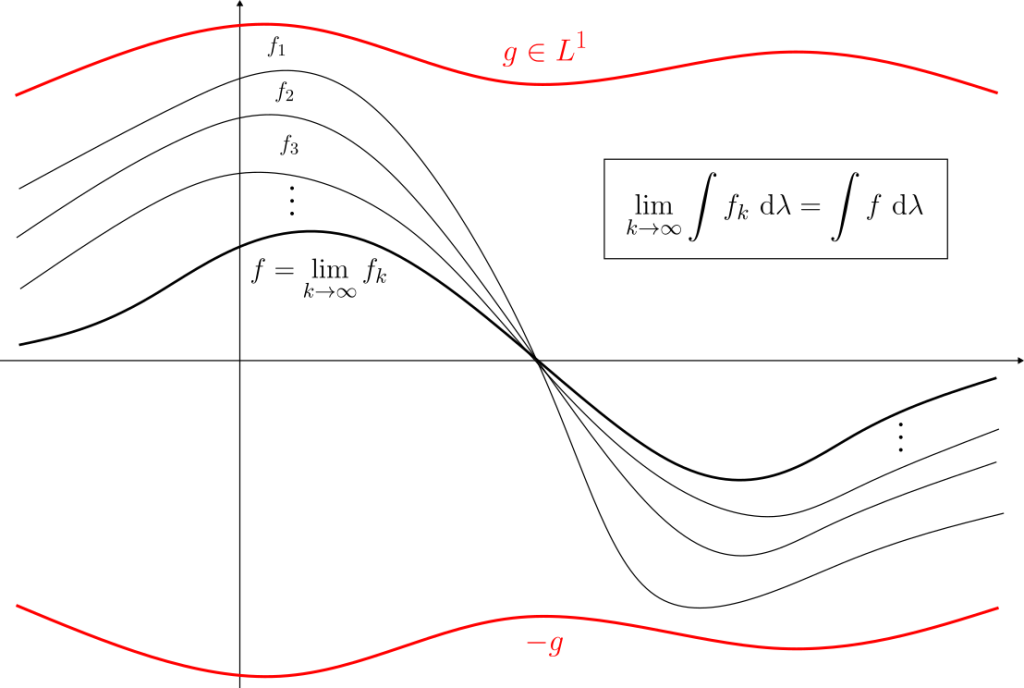
Demostración. Sea $$f=\lim_{k\to \infty} f_k.$$ Ésta es medible al ser el límite de funciones medibles. Más aún, por (1) se sigue que $$0\leq |f|\leq g.$$ Entonces $|f|$ (y en particular $f$) es integrable.
Observemos que la función $g+ f_k$ es medible y no negativa para todo $k$. Aplicando el Lema de Fatou:
$$\int (g+ f) \ \mathrm{d} \lambda\leq \liminf_{k\to \infty} \int (g+ f_k) \ \mathrm{d} \lambda$$
$$\implies \int g \ \mathrm{d} \lambda + \int f \ \mathrm{d} \lambda \leq \int g \ \mathrm{d} \lambda + \liminf_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$
Restando $\int g \ \mathrm{d} \lambda<\infty$ de ambos lados de la desigualdad anterior obtenemos $$ \int f \ \mathrm{d} \lambda \leq \liminf_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$
Similarmente, aplicando el Lema de Fatou a las funciones $g-f_k\geq 0$ resulta $$\int (g- f) \ \mathrm{d} \lambda\leq \liminf_{k\to \infty} \int (g- f_k) \ \mathrm{d} \lambda$$ $$\implies \int g \ \mathrm{d} \lambda – \int f \ \mathrm{d} \lambda \leq \int g \ \mathrm{d} \lambda – \limsup_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$ $$\implies \limsup_{k\to \infty} \int f_k \ \mathrm{d} \lambda \leq \int f \ \mathrm{d} \lambda.$$
(En el segundo renglón usamos que $\liminf_k -a_k=-\limsup a_k$). Combinando las desigualdades obtenidas concluimos que $$ \int f \ \mathrm{d}\lambda \leq \liminf_{k\to \infty} \int f_k \ \mathrm{d} \lambda \leq \limsup_{k\to \infty} \int f_k \ \mathrm{d} \lambda \leq \int f \ {d}\lambda. $$ Es decir, $\lim_k \int f_k \ \mathrm{d}\lambda$ existe y es igual a $$\lim_{k\to \infty} \int f_k \ \mathrm{d} \lambda=\int f \ \mathrm{d} \lambda.$$
$\square$
Algunos ejercicios resueltos
Para fijar ideas, veamos un par de ejercicios resueltos.
Ejercicio. Sea $f\in L^1(\mathbb{R}^n)$ y $A_1\subseteq A_
2\subseteq \dots$ una sucesión creciente de conjuntos medibles tales que $\mathbb{R}^n=\bigcup_{k=1}^{\infty} A_k$. Demuestra que $$\lim_{k\to \infty} \int f\cdot \chi_{A_k} \ \mathrm{d}\mu=\int f \ \mathrm{d}\mu.$$
Solución. Las funciones $f\cdot \chi_{A_k}$ son medibles al ser producto de funciones medibles. Más aún, son integrables pues $$|f\cdot\chi_{A_k}|\leq |f| \ \ \ \ \ \forall k\in \mathbb{N} .$$ Como $f\in L^1$ $\implies$ $|f|\in L^1$, así que el estimado anterior nos dice que podemos «dominar» las funciones $f\cdot \chi_{A_k}$ por la función $g=|f|\in L^1$.
Ahora, como $\bigcup_{k=1}^{\infty} A_k=\mathbb{R}^n$, para cada $x\in \mathbb{R}^n$, existe algún entero $M_x$ suficientemente grande tal que $x\in A_{k}$ para todo $k\geq M_x$. Esto nos dice que $$f(x)\cdot \chi_{A_k}(x)=f(x)\cdot 1 =f(x) \ \ \ \ \ \forall k\geq M_x.$$ Como lo anterior se satisface para cualquier $x\in \mathbb{R}^n$, concluimos que $$\lim_{k\to \infty} (f\cdot \chi_{A_k})=f.$$ Finalmente, aplicando el teorema de la convergencia dominada a la sucesión de funciones $f\cdot \chi_{A_k}$ (tomando $|f|=g\in L^1$ como la función que «domina» a la sucesión), concluimos que $$\lim_{k\to \infty} \int f\cdot \chi_{A_k} \ \mathrm{d}\mu=\int f \ \mathrm{d}\mu.$$
$\triangle$
Observación. En el lenguaje de integración sobre subconjuntos [ENLACE], el resultado anterior se reescribe como: $$\lim_{k\to \infty}\int_{A_k}f \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$
Ejercicio. Sea $f\in L^1(\mathbb{R}^n)$. Demuestra que $$\lim_{k\to \infty} \int f(x)e^{-\frac{|x|^2}{k}} \ \mathrm{d}x = \int f(x) \ \mathrm{d}x.$$
Solución. Consideremos la sucesión de funciones $f_k(x)=f(x)e^{-\frac{|x|^2}{k}}$.
Como $e^{-\frac{|x|^2}{k}}\leq e^0=1$, entonces $|f_k(x)|\leq |f(x)|$ para $k=1,2,\dots$. Es decir, la función $|f|\in L^1$ domina a cada una de las $f_k$. Además $$\lim_{k\to \infty} f_k(x)=f(x)\lim_{k\to \infty} e^{-\frac{|x|^2}{k}} = f(x)\cdot e^0 = f(x).$$ Para todo $x\in \mathbb{R}^n$. Aplicando el teorema de la convergencia dominada:
$$\lim_{k\to \infty} \int f(x)e^{-\frac{|x|^2}{k}} \ \mathrm{d}x= \lim_{k\to \infty} \int f_k(x) \ \mathrm{d} x=\int \left( \lim_{k\to \infty} f_k(x) \right) \ \mathrm{d}x=\int f(x) \ \mathrm{d}x.$$
$\triangle$
Veamos ahora un ejemplo un poco más sofisticado, en el que encontrar la función integrable que «domina» a la sucesión no es del todo inmediata.
Ejercicio. Calcula $$\lim_{k\to \infty} \int_{\mathbb{R}}\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right) \ \mathrm{d}x.$$
Solución. Consideremos la sucesión $f_k(x)=\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right)$. Notemos que para cada $x\in \mathbb{R}$: \begin{equation}\lim_{k\to \infty} f_k(x)=\lim_{k\to \infty}\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right)=e^{-x^2}\sin(0)=0.\end{equation}
(Recuerda que $e^{-x}=\lim_{k\to \infty}\left( 1+\frac{x}{k} \right)^{-k}$). Así que si somos capaces de encontrar una función $g\in L^1$ que domine a la sucesión $f_k$, por el teorema de la convergencia dominada tendríamos que $$\lim_{k\to \infty}\int_{\mathbb{R}}f_k(x) \ \mathrm{d}x=\int 0 \ \mathrm{d}x=0.$$
Proponemos $$g(x)=\frac{1}{1+x^2}.$$
- Veamos que $|f_k(x)|\leq \frac{1}{1+x^2}$ para todo $x\in \mathbb{R}$ y $k\in \mathbb{N}$.
Como $|\sin(x)|\leq 1$ $\forall x$, tenemos que $$|f_k(x)|=\left| \left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right) \right|\leq \left(1+ \frac{x^2}{k} \right)^{-k}.$$
Así que es suficiente probar que $\forall x\in \mathbb{R}$ y $k\in \mathbb{N}$: $$\left(1+ \frac{x^2}{k} \right)^{-k}\leq \frac{1}{1+x^2}$$ $$\iff 1+x^2\leq \left(1+ \frac{x^2}{k} \right)^{k}.$$ Ésto último es inmediato por el teorema del binomio. Los primeros términos de $\left(1+\frac{x^2}{k}\right)^k$ son $1+\binom{k}{1}\left( \frac{x^2}{k}\right)+\dots=1+x^2+\dots$
- Veamos ahora que $g(x)=\frac{1}{1+x^2}\in L^1(\mathbb{R})$.
Más adelante, cuando veamos la equivalencia entre integral de Lebesgue e integral de Riemann, seremos capaces de calcular el valor exacto de dicha integral con muy poco trabajo. Por el momento, podemos estimar la integral con una serie convergente.
Notemos que $0\leq g(x)=\frac{1}{1+x^2}\leq 1$ $\forall x\in \mathbb{R}$. Más aún, si $|x|\geq N$ $\implies$ $|g(x)|=\frac{1}{1+x^2}\leq \frac{1}{N^2}$. Esto nos garantiza que $g(x)\leq s(x)$, donde $s$ es la función «escalonada»: \begin{equation*} s(x)= \begin{cases} 1 & \text{si } x [-1,1) \\ \frac{1}{k^2} & \text{si } x \in [k,k+1),[-(k+1),k) \end{cases} \end{equation*} Invocando el teorema de la convergencia monótona para calcular $\int s \ \mathrm{d}\lambda$ concluimos:
\begin{align*}
\int g \ \mathrm{d}\lambda &\leq \int s \ \mathrm{d}\lambda \\
&= 1\cdot\lambda([-1,1))+\sum_{k=1}^{\infty}\frac{1}{k^2}\cdot\lambda([k,k+1))+\sum_{k=1}^{\infty}\frac{1}{k^2}\cdot\lambda([-(k+1),-k)) \\
&= 2+2\sum_{k=1}^{\infty}\frac{1}{k^2} \\
&< \infty.
\end{align*}
Entonces $g$ satisface las condiciones del teorema de la convergencia dominada y los cálculos en (2) son válidos. Concluimos $$\lim_{k\to \infty} \int_{\mathbb{R}}\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right) \ \mathrm{d}x=0.$$
$\triangle$
Más adelante…
Definiremos el concepto de casi donde sea, un concepto de gran utilidad en la teoría de integración. Daremos versiones más generales de los teoremas de convergencia que hemos probado hasta ahora aprovechando esta idea.