Introduccion
El método de los mínimos cuadrados
El método de mínimos cuadrados se aplica para ajustar rectas a una serie de datos presentados como punto en el plano.
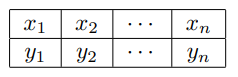
Suponagamos que se tienen los siguientes datos para las variables $x$,$y$.
Esta situación se puede presentar en estudios experimentales, donde se estudia la variación de cierta magnitud x en función de otra magnitud y. Teóricamente es de esperarse que la relación entre estas variables sea lineal, del tipo
$$y=mx+b$$
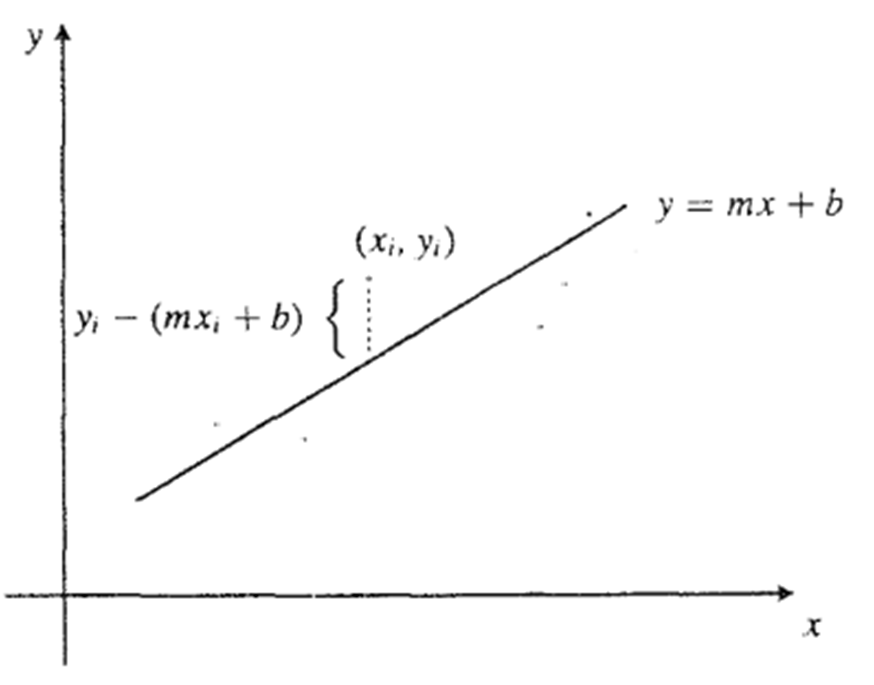
El método de mínimos cuadrados nos proporciona un criterio con el cual podremos obtener la mejor recta que representa a los puntos dados. Se desearía tener
$$y_{i}=mx_{i}+b$$
para todos los puntos $(x_{i},y_{i})$ de $i=1,…,n$. Sin embargo, como en general
$$y_{i}\neq mx_{i}+b$$
se pide que la suma de los cuadrados de las diferencias (las desviaciones)
$$y_{i}-(mx_{i}+b)$$
sea la menor posible.
Se requiere
$$S=(y_{1}-(mx_{1}+b))^{2}+(y_{2}-(mx_{2}+b))^{2}+\cdots+(y_{n}-(mx_{n}+b))^{2}$$
$$=\sum_{i=1}^{n}(y_{i}-(mx_{i}+b))^{2}$$
sea lo más pequeña posible. Los valores de m y b que cumplan con esta propiedad, determinan la recta
$$y=mx+b$$
que mejor representa el comportamiento lineal de los puntos $(x_{i},y_{i})$
Consideremos entonces la función f de las variables m y b dada por
$$f(m,b)=\sum_{i=1}^{n}(y_{i}-(mx_{i}+b))^{2}$$
donde los puntos críticos de esta función se obtienen al resolver el sistema
$$\frac{\partial f}{\partial m}=\sum_{i=1}^{n}2(y_{i}-(mx_{i}+b))(-x_{i})=2\sum_{i=1}^{n}x_{i}(y_{i}-(mx_{i}+b))=0$$
$$\frac{\partial f}{\partial b}=\sum_{i=1}^{n}2(y_{i}-(mx_{i}+b))(-1)=-2\sum_{i=1}^{n}(y_{i}-(mx_{i}+b))=0$$
De la segunda ecuación obtenemos
$$\sum_{i=1}^{n}y_{i}-m\sum_{i=1}^{n}x_{i}-\sum_{i=1}^{n}b=0$$
de donde
$$b=\frac{1}{n}\sum_{i=1}^{n}y_{i}-m\left(\frac{1}{n}\sum_{i=1}^{n}x_{i}\right)$$
Llamemos
$$\overline{x}=\frac{1}{n}\sum_{i=1}^{n}x_{i}$$
$$\overline{y}=\frac{1}{n}\sum_{i=1}^{n}y_{i}$$
que son las medias aritméticas de los valores $x_{i},~y_{i}$ respectivamente. Entonces
$$b=\overline{y}-m\overline{x}$$
sustituyendo en la ecuación
$$\frac{\partial f}{\partial m}=0$$
nos queda
$$\sum_{i=1}^{n}x_{i}(y_{i}-mx_{i}-(\overline{y}-m\overline{x}))=0$$
de donde se obtiene
$$m=\frac{\sum_{i=1}^{n}x_{i}(y_{i}-\overline{y})}{\sum_{i=1}^{n}x_{i}(x_{i}-\overline{x})}$$
En resumen, la función
$$f(m,b)=\sum_{i=1}^{n}(y_{i}-(mx_{i}+b))^{2}$$
tiene un único punto crítico para
$$m=\frac{\sum_{i=1}^{n}x_{i}(y_{i}-\overline{y})}{\sum_{i=1}^{n}x_{i}(x_{i}-\overline{x})},~~~b=\overline{y}-m\overline{x}$$
Ahora vamos a verificar que en dicho punto crítico se alcanza un mínimo local, para lo cual recurrimos a nuestro criterio de la segunda derivada, en este caso
$$\frac{\partial^{2} f}{\partial m^{2}}=-2\sum_{i=1}^{n}-x_{i}^{2}=2\sum_{i=1}^{n}x_{i}^{2}$$
$$\frac{\partial^{2} f}{\partial m \partial b}=-\sum_{i=1}^{n}-x_{i}=2\sum_{i=1}^{n}x_{i}$$
$$\frac{\partial^{2} f}{\partial b^{2}}=-2\sum_{i=1}^{n}(-1)=2n$$
Tenemos que
$$\frac{\partial^{2} f}{\partial m^{2}}>0$$
Por otro lado
$$\left(2\sum_{i=1}^{n}x_{i}\right)^{2}-\left(2\sum_{i=1}^{n}x_{i}^{2}\right)(2n)<0$$
esta desigualdad es equivalente a
$$\left(\sum_{i=1}^{n}x_{i}\right)^{2}<n\sum_{i=1}^{n}x_{i}$$
La cual no es mas que la desigualdad de Cauchy-Schwarz aplicada a los vectores $(1,1,…,1)$ y $(x_{1},x_{2},…,x_{n})$ de $\mathbb{R}^{n}$. Por lo que la función f posee un mínimo local en el punto punto crítico dado.
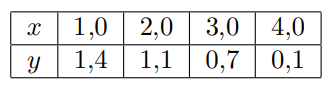
Ejemplo. Se obtuvieron experimentalmente los siguientes valores de las variables x, y, los cuales se sabe que guardan entre sí una relación lineal
Vamos a encontrar la recta que mejor se ajusta a estos datos, según el método de mínimos cuadrados se tiene
$$\overline{x}=\frac{1+2+3+4}{2}=2.5$$
$$\overline{y}=\frac{1.4+1.1+0.7+0.1}{4}=0.825$$
Aplicando la fórmula obtenida para m y b obtenemos
$$m=\frac{\sum_{i=1}^{n}x_{i}(y_{i}-\overline{y})}{\sum_{i=1}^{n}x_{i}(x_{i}-\overline{x})}=\frac{1(1.4-0.825)+2(1.1-0.825)+3(0.7-0.825)+4(0.1-0.825)}{1(1-2.5)+2(2-2.5)+3(3-2.5)+4(4-2.5)}$$
$$=\frac{-2.15}{5}=-0.43$$
$$b=\overline{y}-m\overline{x}=0.825-(0.43)(2.5)=1.9$$
por lo que la recta que mejor ajusta los datos proporcionados
La suma de las diferencias de la recta y real con la y predicha por la ecuación obtenida es
$$-0.07+0.06+0.09-0.08=0$$
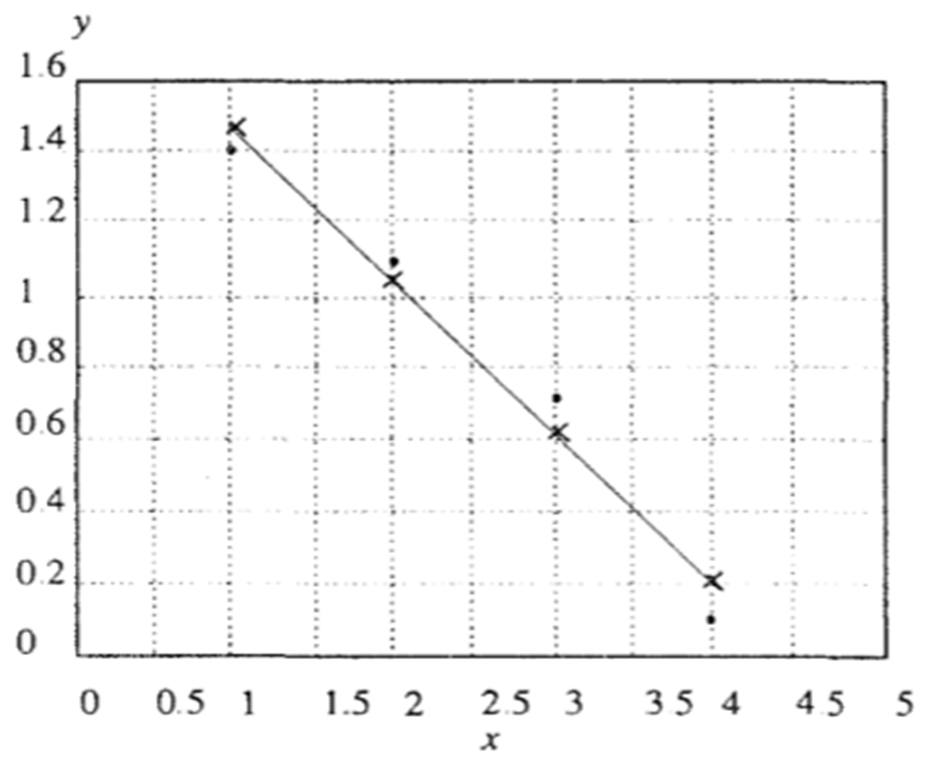
Es decir nuestra recta efectivamente compensa los puntos que quedaron por encima con puntos que quedaron por debajo. Gráficamente esto se ve.
La mejor recta que ajusta los datos del ejemplo.
Mas adelante
Tarea Moral
1.- Explica con tus propias palabras la idea de un punto o puntos críticos de una función entudiado con anterioridad y su relación subyacente con un conjunto de datos dados donde unos dependen de otros (por ejemplo: valores de temperatura y presión). Básicamentte es describir de qué manera interviene el método de mínimos cuadrados en un ajuste lineal, considera como concepto clave el mínimo de una función, en este caso cuando nos presentan varios valores donde dependen unos de otros entre sí, ¿cuál es la función que nos interesa? Nota: en el área de estadística esta herramienta recibe el nombre de regresión lineal simple.
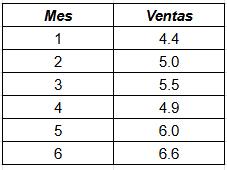
2.- Una empresa de ecommerce desea predecir sus ventas mensuales para el próximo trismestre basándose en los datos de los últimos 6 meses. Se asume que existe una relación lineal entre el tiempo (mes) y las ventas como indica la siguiente tabla:
Determina la recta de la forma $$y=mx+b$$ que mejor se ajusta a los datos
3.- Pronostica la venta para el mes 7.
4.- Grafica los datos para corroborar geométricamente el ejercicio anterior.
5.- Aplica los ejercicios 2 al 4 en python o R de forma extendida, es decir, define y calcula las variables necesarias: $$\overline{x}, \overline{y}, b,m$$