Introducción
En la entrada anterior demostramos el teorema de existencia y unicidad de Picard. Antes de finalizar con el estudio a las ecuaciones diferenciales de primer orden vamos a regresar un momento a la teoría cualitativa de ecuaciones de primer orden, en específico, al estudio de soluciones de ecuaciones autónomas de la forma $$\frac{dy}{dt}=f(y).$$
En muchas ocasiones las ecuaciones diferenciales involucran constantes. Si hacemos variar esta constante obtendremos una familia de ecuaciones diferenciales que dependen de este nuevo parámetro que llamaremos $\lambda$. A esta familia de ecuaciones la denotaremos por $$\frac{dy}{dt}=f_{\lambda}(y).$$
Estudiaremos entonces a esta familia de ecuaciones, y el cambio cualitativo de las soluciones conforme varía el parámetro. Nos interesará conocer el comportamiento de las soluciones de equilibrio, y los cambios que estas tienen dependiendo del valor de $\lambda$. En particular, estudiaremos el cambio en el número de soluciones de equilibrio bajo pequeñas perturbaciones del parámetro $\lambda$. A este tipo de problemas los llamaremos bifurcaciones. Definiremos el concepto de valor de bifurcación, y mostraremos cómo encontrar este valor, tanto de manera gráfica mediante un diagrama, como de manera analítica.
Bifurcaciones y valor de bifurcación
En este video damos una pequeña introducción al concepto de bifurcación, definimos la familia uniparamétrica de ecuaciones autónomas y el valor de bifurcación, todo mediante un ejemplo sencillo.
Diagrama de bifurcaciones
Mostramos un diagrama geométrico para hallar los valores de bifurcación de una familia uniparamétrica de ecuaciones autónomas, y para conocer el comportamiento de las soluciones a las ecuaciones de la familia, sin dibujarlas explícitamente. A este diagrama lo llamamos diagrama de bifurcaciones.
Determinación de los valores de bifurcación
En el último video de esta entrada hallamos los valores bifurcación mediante un análisis a las gráficas de las funciones $f_{\lambda}(y)$ y con ayuda también de la derivada de dichas funciones en determinados puntos.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- Verifica que para toda $\lambda <0$ la ecuación $$\frac{dy}{dt}=y^{2}+\lambda$$ tiene dos soluciones de equilibrio, y para toda $\lambda>0$, la ecuación $$\frac{dy}{dt}=y^{2}+\lambda$$ no tiene soluciones de equilibrio.
- Prueba que $\lambda=0$ es el único valor de bifurcación para la familia $$\frac{dy}{dt}=y^{2}+\lambda.$$
- Muestra, según la definición, que $\lambda=-1$ es valor de bifurcación para la familia de ecuaciones $$\frac{dy}{dt}=\sin{y}+\lambda.$$
- Considera la familia uniparamétrica $$\frac{dy}{dt}=\lambda y-y^{3}.$$ Encuentra las soluciones de equilibrio para todos los valores de $\lambda$, y esboza el diagrama de bifurcaciones.
- Encuentra los valores de bifurcación para la familia uniparamétrica $$\frac{dy}{dt}=y^{4}+\lambda y^{2}$$ con ayuda de la derivada y las gráficas de $f_{\lambda}(y)$. Dibuja el diagrama de bifurcaciones.
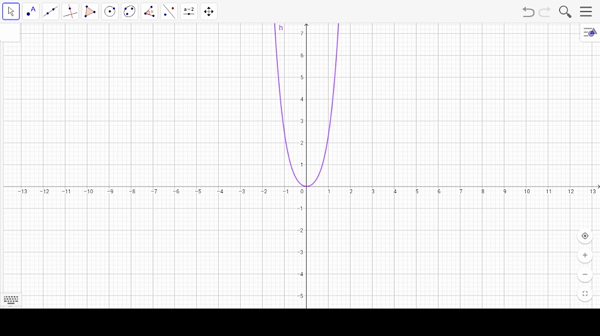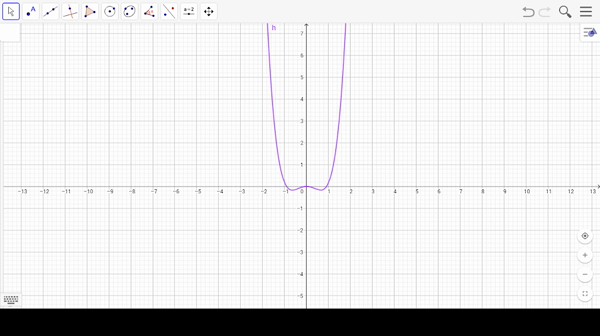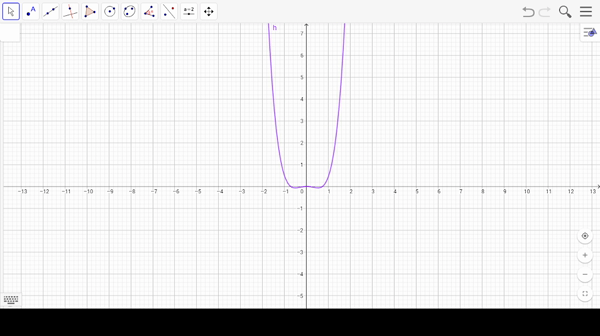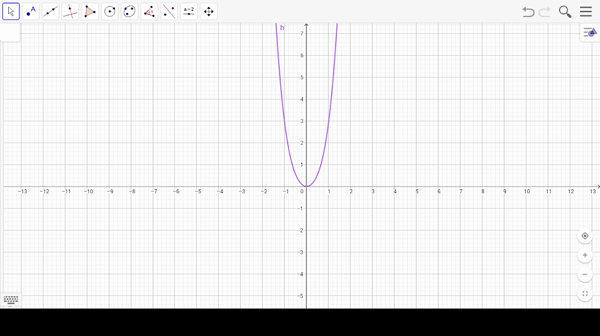
Para encontrar los valores de bifurcación, buscamos valores de $\lambda_{0}$ y $y_{0}$ tales que $$f_{\lambda_{0}}(y_{0})=0 ; \,\,\,\,\,\,\,\, \frac{df_{\lambda_{0}}}{dy}(y_{0})=0. $$ Sin embargo existen casos donde esto último ocurre pero $\lambda_{0}$ no es un valor de bifurcación.
Prueba que las siguientes familias de ecuaciones no tienen valores de bifurcación y dibuja algunas gráficas de estas familias:
- $\frac{dy}{dt}=y^{3}+\lambda$
- $\frac{dy}{dt}=(y+\lambda)^{2}$
Así, en los dos casos, ocurre que $$f_{0}(0)=0 ; \,\,\,\,\,\,\,\, \frac{df_{0}}{dy}(0)=0$$ pero $0$ no es valor de bifurcación.
Más adelante
Con este tema damos por terminado la primera unidad del curso. En la siguiente entrada comenzamos la segunda unidad que tratará de las ecuaciones diferenciales de segundo orden.
En particular, en la siguiente entrada comenzamos con el análisis a las ecuaciones lineales homogéneas de segundo orden con coeficientes constantes.
Entradas relacionadas
- Ir a Ecuaciones Diferenciales I
- Entrada anterior del curso: Teorema de Existencia y Unicidad de Picard
- Siguiente entrada del curso: Ecuaciones lineales homogéneas de segundo orden. Propiedades del conjunto de soluciones
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»
