Introducción
En la entrada anterior desarrollamos un par de técnicas geométricas para conocer las soluciones de una ecuación diferencial de primer orden de la forma $\frac{dy}{dt}=f(t,y)$. En esta ocasión nos enfocaremos en una familia de ecuaciones en particular, que tienen la forma $\frac{dy}{dt}=f(y)$, las cuales llamaremos ecuaciones autónomas. Para conocer sus soluciones de manera geométrica, haremos uso de sus soluciones de equilibrio y su línea fase. Por supuesto definiremos estos conceptos y mediante herramientas de cálculo diferencial podremos hacer un esbozo de las soluciones a dicha ecuación diferencial.
Vamos a comenzar.
Esbozo de las soluciones a una ecuación autónoma mediante el trazo de la línea fase y sus soluciones de equilibrio
En este video definimos a las ecuaciones diferenciales autónomas de primer orden y sus soluciones de equilibrio. Posteriormente, dibujamos la línea fase asociada a la ecuación y con ayuda de esta hacemos un esbozo de las soluciones a la ecuación en el plano $t-y$.
Clasificación de las soluciones de equilibrio
Una vez que conocemos cómo dibujar las soluciones de una ecuación autónoma a partir de su línea fase, clasificamos sus soluciones de equilibrio en tres tipos, según el comportamiento de soluciones cercanas en el plano $t-y$.
Finalizamos con un teorema que nos permitirá conocer el tipo de solución de equilibrio de una ecuación autónoma, mediante el signo de la derivada de la función $f(y)$ evaluada en la solución de equilibrio.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- Encuentra las soluciones de equilibrio y dibuja la línea fase de la ecuación $\frac{dy}{dt}=y^{3}-y^{2}$.
- Considera la ecuación autónoma $\frac{dy}{dt}=\frac{1}{1-y}$. Encuentra sus soluciones de equilibrio (si las tiene) y dibuja la línea fase. Con la información obtenida, analiza cuál es el comportamiento de las soluciones a la ecuación. ¿Cómo crees que se ven las soluciones en el plano $t-y$?
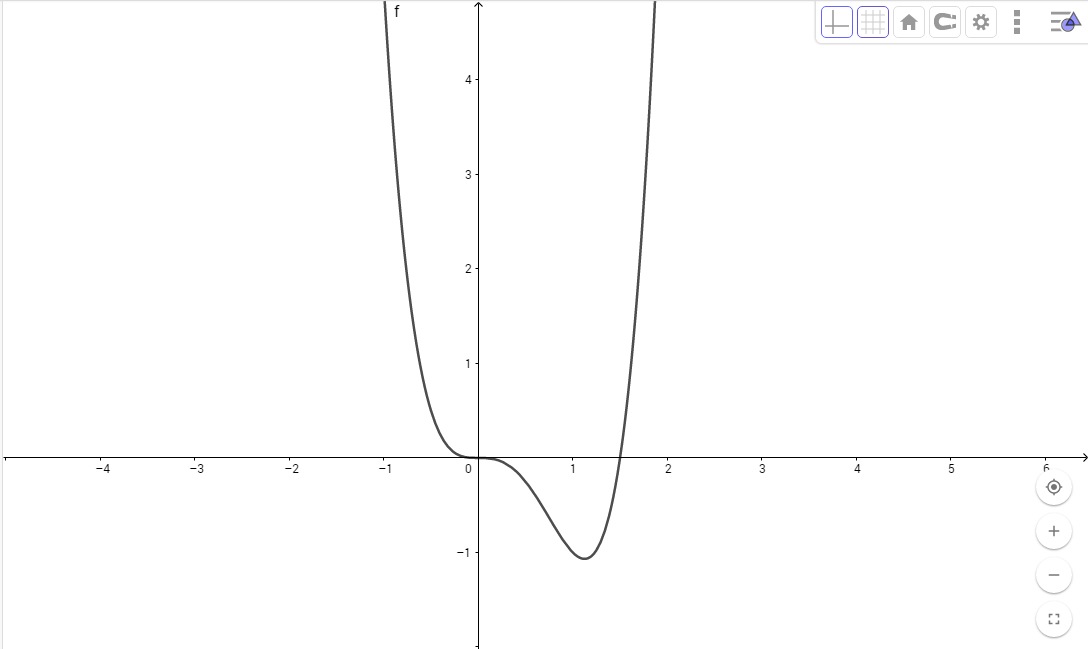
- ¿Cómo dibujarías las soluciones a la ecuación $\frac{dy}{dt}=f(y)$ si $f$ tiene la siguiente gráfica? Hint: Recuerda los criterios de los signos de las derivadas de primer orden en un punto que nos ayudan a ver cuándo la función es creciente o decreciente en dicho punto.
- Da ejemplos donde $\frac{dy}{dt}=f(y)$, $y_{0}$ es solución de equilibrio de la ecuación diferencial, $f'(y_{0})=0$ y $y_{0}$ sea atractor, repulsor o nodo.
- Clasifica las soluciones de equilibrio del tercer ejercicio.
Más adelante
Ahora que hemos visto varias técnicas para encontrar las soluciones a una ecuación de primer orden, al menos de manera geométrica, nos enfocaremos en la parte analítica de las soluciones.
En el próximo video nos enfocaremos en las ecuaciones lineales homogéneas, y la técnica para resolverlas.
Entradas relacionadas
- Ir a Ecuaciones Diferenciales I
- Entrada anterior del curso: Campo de pendientes asociado a una ecuación diferencial, curvas integrales y método de las isoclinas
- Siguiente entrada del curso: Ecuaciones lineales homogéneas de primer orden
- Notas escritas relacionadas con el tema: Ecuaciones diferenciales autónomas
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»
