Introducción

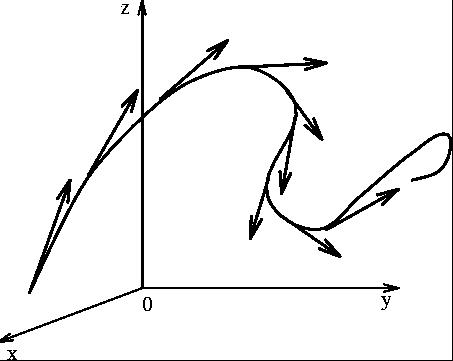
En una recta, el vector unitario tangente $T$ no cambia su dirección y por tanto $T^{\prime}=0$. Si la curva no es una linea recta, la derivada $T^{\prime}$ mide la tendencia de la tangente a cambiar su dirección. El coeficiente de variación o derivada de la tangente unitaria respecto a la longitud de arco se denomina vector curvatura de la curva. Se designa por $\displaystyle{dT/ds}$ donde s representa la
longitud de arco.

Sea $f:[a,b]\subset\mathbb{R}\rightarrow\mathbb{R}^{n}$ una curva dos veces diferenciable parametrizada por longitud de arco y T su vector tangente unitario. La curvatura de f es la función
$$\kappa=\left\|\frac{dT}{ds}\right\|=\|f^{\prime\prime}(s)\|$$
La letra $\kappa$ es la letra griega kappa. La curvatura mide la flexión de la curva.
Mostraremos que una recta, es una curva que no se flexiona, tiene curvatura 0
Ejemplo. Calcule la curvatura en todo punto de la recta $f(t)=(x_{0},y_{0},z_{0})+t(u_{1},u_{u},u_{3})$ donde $\|u\|=1$
tenemos:
\[ f^{\prime}(t)=(u_{1},u_{2},u_{3})\ \ \ \ \ \text{y}\ \ \ \ \ \|f^{\prime}(t)\|=\|u\|=1
\]
Por lo tanto la curva esta parametrizada por longitud de arco
Por lo tanto $\kappa=\|f^{\prime\prime}(t)\|=0$, por lo tanto
$\kappa=0$.$~~\blacksquare$
Ejemplo Calcule la curvatura de una circunferencia. Para un círculo de radio $R$ dado por la ecuación
$$f(t)=(R\cos t,R \sin t)$$
tenemos:
La parametrizacion por longitud de arco es:
$$s=\int_{0}^{t}\|f'(u)\|du=\int_{0}^{t}Rdt=Rt~\rightarrow~s=Rt~\Rightarrow~t=\frac{s}{R}$$
de esta manera se tiene
\begin{align*} \overline{f}(s) &=f\left(\frac{s}{R}\right)=\left(R\cos\left(\frac{s}{R}\right),R\sin\left(\frac{s}{R}\right)\right) \\ \overline{f}^{\prime}(s)&=\left(-\sin \left(\frac{s}{R}\right), \cos \left(\frac{s}{R}\right)\right) \\ \overline{f}^{\prime\prime}(s)&=\left(-\frac{1}{R}\cos \left(\frac{s}{R}\right),-\frac{1}{R} \sin \left(\frac{s}{R}\right)\right) \end{align*}
Por lo tanto $\displaystyle{\kappa=\|\overline{f}^{\prime\prime}(s)\|=\frac{1}{R}}$.
Esto prueba que una circunferencia tiene curvatura constante.
El siguiente teorema nos proporciona otras fórmulas que nos permiten calcular la
curvatura parametrizada por otro parámetro t, que no es necesariamente la longitud
de arco.
Teorema. Sea $f(t)$ una curva dos veces diferenciable. Entonces
$$\kappa(t)=\frac{\|T'(t)\|}{\|f'(t)\|}$$
Demostración. Sabemos que $\displaystyle{s^{\prime}(t)=\|f^{\prime}(t)\|}$. Además usando la regla de la cadena
$\begin{align*} T'(t)&=\frac{dT}{dt}=\frac{dT}{ds}\frac{ds}{dt}=\frac{dT}{ds}\|f'(t)\| \\ &~\Rightarrow~\frac{dT}{ds}=\frac{T'(t)}{\|f'(t)\|} \\ &~\Rightarrow~\left\|\frac{dT}{ds}\right\|=\frac{\|T'(t)\|}{\|f'(t)\|} \\ &~\Rightarrow~\kappa(t)=\frac{\|T'(t)\|}{\|f'(t)\|}.~~ \blacksquare \end{align*}$
Ejemplo.
Calcule la curvatura $\kappa$ de la hélice
$x(t)=a\cos(wt)$, $y(t=a\sin(wt))$, $z(t)=bt$.
Solución. Tenemos que: \[f^{\prime}(t)=(-wa\sin(wt),aw\cos(wt),b)\ \ \Rightarrow\ \ \|f^{\prime}(t)\|=\sqrt{a^2w^2+b^2}\] Por lo tanto \[ T=(-aw\sin(wt),aw\cos(wt),b)\frac{1}{\sqrt{a^2w^2+b^2}} \] Por lo tanto \[ k=\frac{\|T^{\prime}\|}{\|f^{\prime}\|}= \|-aw^2\cos(wt),-aw^2\sin(wt),0\|\frac{1}{\sqrt{a^2w^2+b^2}}= \] \[ =\sqrt{(aw^2)^2(\cos^2(wt)+\sin^2(wt))}\ \frac{1}{\sqrt{a^2w^2+b^2}}= \frac{aw^2}{\sqrt{a^2w^2+b^2}}.~~ \blacksquare \]

Teorema . Sea $f(t)$ una curva dos veces diferenciable. Entonces
$$\kappa(t)=\frac{\|f^{\prime}(t)\times f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{3}}$$
Demostración. Si $$T=\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\Rightarrow
T~\|f^{\prime}(t)\|=f^{\prime}(t)\Rightarrow
T\frac{ds}{dt}=f^{\prime}(t)$$Por lo tanto
$$f^{\prime\prime}(t)=T\frac{d^{2}s}{dt^{2}}+\frac{ds}{dt}T^{\prime}$$
Haciendo el producto cruz $$f^{\prime}(t)\times
f^{\prime\prime}(t)=T\frac{ds}{dt}\times
\left(T\frac{d^{2}s}{dt^{2}}+\frac{ds}{dt}T^{\prime}\right)=\cancel{T\frac{ds}{dt}\times
T\frac{d^{2}s}{dt^{2}}}+T\frac{ds}{dt}\times
\frac{ds}{dt}T^{\prime}$$Por lo tanto
$$\|f^{\prime}(t)\times f^{\prime\prime}(t)\|=\left\|T\frac{ds}{dt}\times
\frac{ds}{dt}T^{\prime}\right\|=\left(\frac{ds}{dt}\right)\left\|T\right\|\left(\frac{ds}{dt}\right)\left\|T^{\prime}\right\|\sin(T,T^{\prime})=\left(\frac{ds}{dt}\right)^{2}\left\|T^{\prime}\right\|$$En
cosecuencia$$\frac{\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|}{\left(\frac{ds}{dt}\right)^{2}}=\|T^{\prime}|\Rightarrow
\|T^{\prime}\|=\frac{\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{2}}$$ sustituimos en
$$k(t)=\frac{\|T^{\prime}(t)\|}{\|f^{\prime}(t)\|}\Rightarrow \kappa(t)=\frac{\frac{\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{2}}}{\|f^{\prime}(t)\|}\Rightarrow
\kappa(t)=\frac{\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{3}}.~~ \blacksquare $$
Ejemplo. Hallar la función curvatura $\kappa(t)$ de la curva
$$f(t)=\left(t^{2},t,\frac{2t^{3}}{3}\right)$$
Solución. Según la fórmula anterior
\begin{align*} f'(t) & =(2t,1,2t^{2}) \\\ f^{\prime\prime}(t) & =(2,0,4t) \\ \|f'(t)\| & =\sqrt{4t^{2}+1+4t^{4}}=2t^{2}+1 \end{align*}
Por lo que
\begin{align*} f'(t)\times f^{\prime\prime}(t) & =\left|\begin{matrix}i&j&k\\2t&1&2t^{2}\\2&0&4t\end{matrix}\right| \\ & =2(2t,-2t^{2},-1) \\ \|f'(t)\times f^{\prime\prime}(t)\|&=2\sqrt{4t^{2}+4t^{4}+1}=2(2t^{2}+1) \end{align*}
Luego
$$\kappa(t)=\frac{\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{3}}=\frac{2(2t^{2}+1)}{(2t^{2}+1)^{3}}=\frac{2}{(2t^{2}+1)^{2}}.~~ \blacksquare $$
Ejemplo. Para el caso especial de una curva plana con ecuación $y=f(x)$ podemos escoger $x$ como el parámetro y escribir $r(x)=x\hat{i}+f(x)\hat{j}$ entonces
\begin{align*}r^{\prime}(x)&=\hat{i}+f^{\prime}(x)\hat{j}\\r^{\prime
\prime}(x)&=f^{\prime \prime}(x)\hat{j}\end{align*} y al efectuar:
\[
r^{\prime}(x)\ \text{x}\ r^{\prime \prime}(x)=
\left|
\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & f^{\prime}(x) & 0 \\
0 & f^{\prime \prime}(x) & 0 \\
\end{array}
\right|= f^{\prime \prime}(x)\hat{k}
\]

Por lo tanto $\|r^{\prime}(x)\ \times r^{\prime\prime}(x)\|=|f^{\prime\prime}(x)|$.
Por lo tanto, para una curva plana
\[
\kappa(x)=\frac{\|r'(t)\times r^{\prime\prime}(t)\|}{\|r'(t)\|^{3}}=\frac{|f^{\prime\prime}(x)|}{\left(1+[f^{\prime}(x)]^2\right)^{3/2}}.~~ \blacksquare
\]
Ejemplo. Calcular la curvatura del gráfico $f(x)=e^{-x}$.
Solución. Tenemos que: $f'(x)=-e^{-x}$ y $f^{\prime\prime}(x)=e^{-x}$. Luego
$$\kappa(x)=\frac{|f^{\prime\prime}(x)|}{\left[1+\left(f'(x)\right)^{2}\right]^{\frac{3}{2}}}=\frac{e^{-x}}{\left[1+\left(-e^{-x}\right)^{2}\right]^{\frac{3}{2}}}=\frac{e^{-x}}{\left[e^{-2x}+1\right]^{\frac{3}{2}}}.~~ \blacksquare$$

Circunferencia y radio de curvatura

Sea $f:[a,b]\rightarrow\mathbb{R}^{2}$ una curva plana y un punto $P$ sobre una curva plana donde $\kappa\neq 0$. Se llama circunferencia de curvatura o circunferencia osculadora de la curva en el punto P a la circunferencia que cumple las siguientes condiciones:
(a) Es tangente a la curva en P. (la circunferencia y la curva tienen la misma recta tangente en el punto P).
(b) Tiene la misma curvatura ($\kappa$) que la curva en P.
(c) Se encuentra hacia el lado concavo o interior de la curva.
(d) El radio de la curvatura de la curva P es el radio del círculo de curvatura o círculo osculador. $$\rho(t)=\frac{1}{\kappa(t)}$$

Asi el centro del círculo osculador (llamado centro de curvatura)
debe estar en:

\[
c(t)=f(t)+\frac{1}{k(t)}N(t)
\]
Ejemplo. Determine los vectores $T$ y $N$, la curvatura $k$, el centro de la curvatura y la circunferencia osculadora de la parábola $y=x^2$ en el punto $(1,1)$.
Solución. Si la parábola esta
parametrizada por $x=t$ y por $y=t^2$, entonces su vector de
posición es $f(t)=(t,t^2)$, por lo tanto
\begin{align*}f(t)=(t,t^2)&\Rightarrow f^{\prime}(t)=(1,2t)\\&\Rightarrow\|f^{\prime}(t)\|=\sqrt{1+4t^2}\\&\Rightarrow f^{\prime\prime}(t)=(0,2)\end{align*}
por lo tanto:
\[ T(t)=\frac{(1,2t)}{\sqrt{1+4t^2}}\ \ \ \ \ \ \ T(1)=\left(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}}\right)\ \ \ \ \ \ \ N(1)=\left(\frac{-2}{\sqrt{5}},\frac{1}{\sqrt{5}}\right) \] la curvatura $\kappa$, \[ k=\frac{\|f^{\prime\prime}(t)\|}{\left(\sqrt{1+[f^{\prime}(t)]^2}\right)^3}= \frac{2}{\left(\sqrt{1+4t^2}\right)^3}\ \ \ \ \ \ \ k(1)=\frac{2}{5\sqrt{5}}\ \ \Rightarrow\ \ \rho=\frac{5\sqrt{5}}{2} \] Por lo tanto el centro de la curvatura es \[ c(t)=f(1,1)+\frac{1}{\frac{2}{5\sqrt{5}}}\left(\frac{-2}{\sqrt{5}},\frac{1}{\sqrt{5}}\right)= \left(-4,\frac{7}{2}\right) \] Y la ecuación del círculo osculador a la parábola es, por tanto: \[ (x+4)^2+\left(y-\frac{7}{2}\right)^2= \left(\frac{5\sqrt{5}}{2}\right)^2=\frac{125}{4}.~~ \blacksquare \]

Torsión

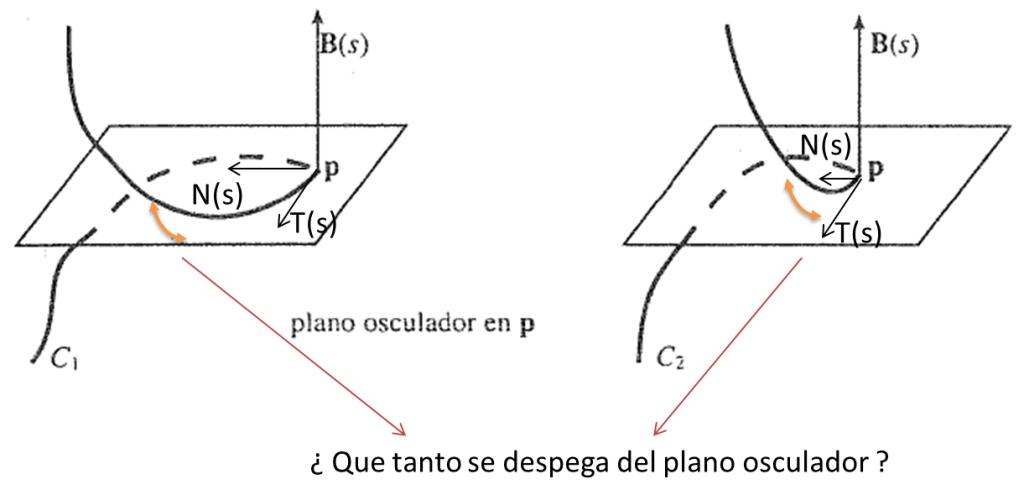
Sea $f:I\subset \mathbb{R}\rightarrow \mathbb{R}^{3}$ una curva tres veces diferenciable parametrizada por longitud de arco. Nuestro objetivo consistira en estimar con que rapidez una curva se aleja de su plano osculador

La forma de medir la rapidez de alejamiento de la curva f de su plano osculador es por medio del vector binormal $B(s)=T(s)\times N(s)$, que sabemos es un vector unitario ortogonal al plano osculador de f en P. Puesto que $\|B(s)\|=1$, $\forall~s\in I$, la magnitud de la derivada $\|B'(s)\|$ de $B(s)$ medirá precisamente la rapidez con la que el vector binormal $B(s)$ está cambiando de dirección en los alrededores del punto estudiado.
Puesto que $B(s)=T(s)\times N(s)$, tenemos, derivando
$$B'(s)=T(s)\times N'(s)+T'(s)\times N(s)$$
El sumando $T'(s)\times N(s)$ que aparece en esta expresión es igual a cero, ya que $T'(s)=f^{\prime\prime}(s)$ es un vector en la dirección de $N(s)$ (y por lo tanto son colineales; por lo que su producto cruz es cero). Entonces nos queda
$$B'(s)=T(s)\times N'(s)$$
También tenemos que
$$\|B\|=1~\Rightarrow~\frac{d \|B\|^{2}}{ds}=0~\Rightarrow~\frac{d(B\cdot B)}{ds}=0~\Rightarrow~B\cdot B’+B’\cdot B=0~\Rightarrow~B’\cdot B=0~\Rightarrow~B’\bot B $$ Esto nos permite concluir que $B'(s)$ es un vector en el plano osculador de f en s. Por otro lado $$B\cdot T=0~\Rightarrow~(B\cdot T)’=0~\Rightarrow~B’\cdot T+T’\cdot B=0~\underbrace{\Rightarrow}_{\textcolor{red}{T’\cdot B=N~ \|T’\|\cdot B=0}}~B’\cdot T=0~\Rightarrow~B’\bot T$$
De lo anterior podemos concluir que $B’$ tiene la dirección del vector $N$. Debe entonces existir un escalar $\tau(s)$ tal que
$$B'(s)=\tau(s)N(s)$$
Definición. Sea $f:I\subset \mathbb{R}\rightarrow \mathbb{R}^{3}$ una curva tres veces diferenciable parametrizada por longitud de arco tal que $f»(s)\neq 0$ $\forall~s\in I$. El número $\tau(s)$ tal que $B'(s)=-\tau(s)N(s)$ se llama torsión de f en s.
Notese que
$$\|B'(s)\|=|\tau(s)|$$
Ejemplo. Dada la función
$$f(t)=(\cos(t),\sin(t),t)$$
cuya reparametrización por longitud de arco es:
$$\overline{f}(s)=\left(\cos\left(\frac{s}{\sqrt{2}}\right),\sin\left(\frac{s}{\sqrt{2}}\right),\frac{s}{\sqrt{2}}\right)$$
cuyo vector normal es
$$N(s)=\left(-\cos\left(\frac{s}{\sqrt{2}}\right),-\sin\left(\frac{s}{\sqrt{2}}\right),0\right)$$
cuyo vector binormal es
$$B(s)=\frac{1}{\sqrt{2}}\left(\sin\left(\frac{s}{\sqrt{2}}\right),-\cos\left(\frac{s}{\sqrt{2}}\right),1\right)$$
de modo que
$$B'(s)=\frac{1}{2}\left(\cos\left(\frac{s}{\sqrt{2}}\right),\sin\left(\frac{s}{\sqrt{2}}\right),0\right)$$
y por lo tanto se tiene
$$|\tau(s)|=\|B'(s)\|=\frac{1}{2}.~~ \blacksquare$$
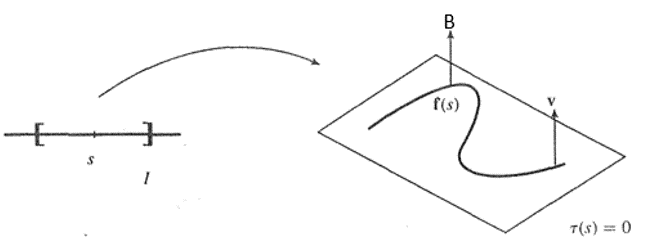
Una curva es plana (es decir, es la imagen de un camino $f:[a,b]\rightarrow\mathbb{R}^{3}$ tal que f(s) se encuentra en un plano en $\mathbb{R}^{3}$ para toda $s\in [a,b]$) si y sólo si su torsión es igual a cero $(\forall~s\in [a,b])$.
En efecto, si $\tau(s)=0$, se tiene que $B'(s)=0$, por lo que el vector binormal $B(s)$ debe ser constante, es decir $B(s)=v$ para todo $s\in[a,b]$. De aquí se tiene que
$$f'(s)\cdot B(s)=f'(s)\cdot v=0~~~\forall~s\in[a,b]$$
(pues $f'(s)$ es ortogonal a $B(s)$), o sea
$$\frac{d(f(s)\cdot v)}{ds}=0$$
de donde $f(s)\cdot v=cte~~~\forall~s\in[a,b]$, y por lo tanto, concluimos que $f(s)$ se encuentra en el plano cuyo vector normal es v, $\forall~s\in[a,b]$.

Recíprocamente, si $f(s)$ se encuentra en un plano para toda s en $[a,b]$, entonces dicho plano es el plano osculador de la curva en todo punto de ella, por tanto el vector unitario $B(s)$ no cambia de dirección, por lo que $B'(s)=0$. de donde $\tau(s)=0$ para toda s en $[a,b]$. $\blacksquare$

Fórmula para calcular la Torsión en términos de la parametrización por longitud de arco

La torsión representa una variación en la dirección del vector binormal, procederemos ahora a desarrollar una fórmula para calcularla
Sea $\overline{f}:[a,b]\rightarrow\mathbb{R}^{3}$ la reparametrización por longitud de arco de f, $\overline{f}=f\circ\varphi$. Queremos calcular la torsión de f en t, donde $t=\varphi(s)$. Sabemos que
\begin{align*} T(s) & =\overline{f}'(s)=\frac{f'(t)}{\|f'(t)\|} \\ T'(s)&=\overline{f}»(s)=\frac{d\left(\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)}{ds} \\ &=\frac{d\left(\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)}{dt}\frac{dt}{ds}=\frac{d\left(\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)}{dt}\frac{1}{\frac{ds}{dt}}\\ &=\frac{d\left(\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)}{dt}\frac{1}{\varphi^{\prime}(s)}\\ &=\frac{d\left(\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)}{dt}\frac{1}{\|f^{\prime}(t)\|}\\ &=\left(\frac{\|f^{\prime}(t)\|f^{\prime\prime}-f^{\prime}(t)\frac{d\left(\|f^{\prime}(t)\|\right)}{dt}}{\|f^{\prime}(t)\|^{2}}\right)\frac{1}{\|f^{\prime}(t)\|}\\ &=\left(\frac{\|f^{\prime}(t)\|f^{\prime\prime}-f^{\prime}(t)\frac{f^{\prime}\cdot f^{\prime\prime}}{\|f^{\prime}(t)\|}}{\|f^{\prime}(t)|^{2}}\right)\frac{1}{\|f^{\prime}(t)\|}~~\left(\frac{d\left(\|f^{\prime}(t)\|\right)}{dt}=\frac{d\sqrt{f^{\prime}(t)\cdot f^{\prime}(t)}}{dt}=\frac{f^{\prime}(t)\cdot f^{\prime\prime}(t)}{\|f^{\prime}(t)\|}\right)\\ &=\left(\frac{\|f^{\prime}(t)\|^{2}f^{\prime\prime}-\left(f^{\prime}(t)\cdot f^{\prime\prime}(t)\right)f^{\prime}(t)}{\|f^{\prime}(t)\|}\right)\frac{1}{\|f^{\prime}(t)\|^{3}}\\ &=\frac{1}{\|f^{\prime}(t)\|^{4}}\left(\|f^{\prime}(t)\|^{2}f^{\prime\prime}(t)-\left(f^{\prime}(t)\cdot f^{\prime\prime}(t)\right)f^{\prime}(t)\right)\\ N(s) &=\frac{\overline{f}^{\prime\prime}(s)}{\kappa(s)} =\frac{\overline{f}^{\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|} \end{align*}
calculemos
$$B'(s)=T(s)\times N'(s)$$ en este caso
\begin{align*} N^{\prime}(s) & =\frac{\|\overline{f}^{\prime\prime}(s)\|\overline{f}^{\prime\prime\prime}(s)-\overline{f}^{\prime\prime}(s)\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|}\right)}{\|\overline{f}^{\prime\prime}(s)\|^{2}} \\ &=\frac{\overline{f}^{\prime\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|}-\overline{f}^{\prime\prime}(s)\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|^{3}}\right) \end{align*}
Luego si $B^{\prime}(s)=T(s) \times N^{\prime}(s)$ entonces se tiene que
\begin{align*} B^{\prime}(s) &=\overline{f}^{\prime}(s)\times \left(\frac{\overline{f}^{\prime\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|}-\overline{f}^{\prime\prime}(s)\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|^{3}}\right)\right) \\ &=\frac{1}{|\overline{f}^{\prime\prime}(s)|}\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime\prime}(s)-\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|^{3}}\right)\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime}(s) \end{align*}
La torsión esta dada por
\begin{align*} B^{\prime}(s) &=\tau(s)N(s) \\ &\Rightarrow B^{\prime}(s)\cdot N(s)=\tau(s)N(s)\cdot N(s) \\ &\Rightarrow B^{\prime}(s)\cdot N(s)=\tau(s)\|N(s)\|^{2} \\ &\Rightarrow B^{\prime}(s)\cdot N(s)=|\tau(s)| \end{align*}
Entonces
\begin{align*} \tau(s) &=B^{\prime}(s)\cdot N(s) \\ &=\left(\frac{1}{\|\overline{f}^{\prime\prime}(s)\|}\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime\prime}(s)-\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|^{3}}\right)f^{\prime}(s)\times \overline{f}^{\prime\prime}(s)\right)\cdot \frac{\overline{f}^{\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|} \\ &=\frac{1}{\|\overline{f}^{\prime\prime}(s)\|^{2}}\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime\prime}(s)\cdot \overline{f}^{\prime\prime}(s)-\cancel{\left(\frac{\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{\|\overline{f}^{\prime\prime}(s)\|^{4}}\right)\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime}(s)} \\ &=\frac{1}{\|\overline{f}^{\prime\prime}(s)\|^{2}}\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime\prime}(s)\cdot \overline{f}^{\prime\prime}(s) \end{align*}
La cancelación es porque $$\overline{f}^{\prime}(s)\times \overline{f}^{\prime\prime}(s)\cdot
\overline{f}^{\prime\prime}(s)=0$$ y como $$k(s)=\|\overline{f}^{\prime\prime}\|$$ se
tiene entonces que $$\boxed{\tau(s)=\frac{\overline{f}^{\prime}(s)\times
\overline{f}^{\prime\prime\prime}(s)\cdot \overline{f}^{\prime\prime}(s)}{k(s)^{2}}=-\frac{\overline{f}^{\prime}(s)\times
\overline{f}^{\prime\prime}(s)\cdot \overline{f}^{\prime\prime\prime}(s)}{k(s)^{2}}}$$

Fórmula para calcular la Torsión en términos del parámetro t

Ahora vamos a expresar la torsión en términos de t. Ya hemos visto que
\begin{align*} \overline{f}^{\prime}(s)&=\frac{f^{\prime}(t)}{|f^{\prime}(t)|} \\ f^{\prime\prime}(s) & =\frac{1}{\|f^{\prime}(t)\|^{4}}\left(|f^{\prime}(t)|^{2}f^{\prime\prime}(t)-\left(f^{\prime}(t)\cdot f^{\prime\prime}(t)\right)f^{\prime}(t)\right) \end{align*}
Por lo tanto
\begin{align*} f^{\prime}(s)\times f^{\prime\prime}(s) &=\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\times \left(\frac{1}{\|f^{\prime}\|^{4}}\left(\|f^{\prime}(t)\|^{2}f^{\prime\prime}(t)-\left(f^{\prime}(t)\cdot f^{\prime\prime}(t)\right)f^{\prime}(t)\right)\right) \\ &=\left(\frac{1}{\|f^{\prime}(t)\|^{3}}\right)f^{\prime}(t)\times f^{\prime\prime}(t)-\left(\frac{f^{\prime}(t)\cdot f^{\prime\prime}(t)}{\|f^{\prime}(t)\|^{5}}\right)\cancel{f^{\prime}(t)\times f^{\prime}(t)} \\ &=\left(\frac{1}{\|f^{\prime}(t)\|^{3}}\right)f^{\prime}(t)\times f^{\prime\prime}(t) \end{align*}
Mientras que
\begin{align*} f^{\prime\prime\prime}(s) &=\frac{df^{\prime\prime}(s)}{ds}=\left(\frac{df^{\prime\prime}(s)}{dt}\right)\frac{dt}{ds}=\left(\frac{df^{\prime\prime}(s)}{dt}\right)\frac{1}{\frac{ds}{dt}} \\ &=\left(\frac{df^{\prime\prime}(s)}{dt}\right)\frac{1}{\|f^{\prime}(t)\|} \\ &=\frac{1}{\|f^{\prime}(t)\|}\frac{d}{dt}\left(\frac{1}{\|f^{\prime}\|^{4}}\left(\|f^{\prime}(t)\|^{2}f^{\prime\prime}(t)-\left(f^{\prime}(t)\cdot f^{\prime\prime}(t)\right)f^{\prime}(t)\right)\right) \\ &=\left(\frac{1}{\|f^{\prime}(t)\|}\right)\left[\left(\frac{1}{\|f^{\prime}(t)\|^{2}}f^{\prime\prime}(t)\right)+\left(\frac{1}{\|f^{\prime}(t)\|^{2}}\right)^{\prime}f^{\prime\prime}(t)\right. \\ &\left.-\left(\frac{f^{\prime}(t)\cdot f^{\prime\prime}(t)}{\|f^{\prime}(t)\|^{4}}\right)f^{\prime\prime}(t)-f^{\prime}(t)\left(\frac{f^{\prime}(t)\cdot f^{\prime\prime}(t)}{\|f^{\prime}(t)\|^{4}}\right)^{\prime}~\right] \end{align*}
Por lo tanto
\begin{align*} f^{\prime}(s)\times f^{\prime\prime}(s)\cdot f^{\prime\prime\prime}(s) &=\left(\frac{1}{\|f^{\prime}(t)\|^{3}}\right)f^{\prime}(t)\times f^{\prime\prime}(t)\cdot \left(\frac{1}{\|f^{\prime}(t)\|}\right)\left[\left(\frac{1}{\|f^{\prime}(t)\|^{2}}f^{\prime\prime}(t)\right)\right. \\ &\left.+\cancel{\left(\frac{1}{\|f^{\prime}(t)\|^{2}}\right)^{\prime}f^{\prime\prime}(t)}-\cancel{\left(\frac{f^{\prime}(t)\cdot f^{\prime\prime}(t)}{\|f^{\prime}(t)\|^{4}}\right)f^{\prime\prime}(t)}-\cancel{f^{\prime}(t)\left(\frac{f^{\prime}(t)\cdot f^{\prime\prime}}{\|f^{\prime}(t)\|^{4}}\right)^{\prime}}~\right] \\ &=\frac{1}{\|f^{\prime}(t)\|^{3}}f^{\prime}(t)\times f^{\prime\prime}(t)\cdot \frac{1}{\|f^{\prime}(t)\|^{3}}f^{\prime\prime\prime}(t) \\ &=\frac{1}{\|f^{\prime}(t)\|^{6}}f^{\prime}(t)\times f^{\prime\prime}(t)\cdot f^{\prime\prime\prime}(t) \end{align*}
finalmente
\begin{align*} \tau(t) &=\frac{f^{\prime}(s)\times f^{\prime\prime\prime}(s)\cdot f^{\prime\prime}(s)}{k(s)^{2}} \\ &=-\frac{f^{\prime}(s)\times f^{\prime\prime}(s)\cdot f^{\prime\prime\prime}(s)}{k(s)^{2}} \\ &=-\frac{1}{\|f^{\prime}(t)\|^{6}}\frac{f^{\prime}(t)\times f^{\prime\prime}(t)\cdot f^{\prime\prime\prime}}{\left(\frac{\|f^{\prime}\times f^{\prime\prime}(t)\|}{\|f^{\prime}(t)\|^{3}}\right)^{2}} \end{align*}
Tenemos que
la torsión esta dada por $$\boxed{\tau(t)=-\frac{f^{\prime}(t)\times
f^{\prime\prime}(t)\cdot
f^{\prime\prime\prime}(t)}{\left(\|f^{\prime}(t)\times
f^{\prime\prime}(t)\|\right)^{2}}}$$
Ejemplo. Probar que la torsión de la hélice $f(t)=(a\cos(t),a\sin(t),bt)$ es
$$\tau(t)=\frac{b}{a^{2}+b^{2}}$$
Solución. En este caso
\begin{align*} f'(t) & =(-a\sin(t),a\cos(t),b) \\ f^{\prime\prime}(t) & =(-a\cos(t),-a\sin(t),0) \\ f^{\prime\prime\prime}(t) & =(a\sin(t),-a\cos(t),0) \end{align*}
Por lo que
$$f'(t)\times f^{\prime\prime}(t)=\left|\begin{matrix}i&j&k\\-a\sin(t)&a\cos(t)&b\\-a\cos(t)&-a\sin(t)&0\end{matrix}\right|=(ab\sin(t),-ab\cos(t),a^{2})$$
tenemos entonces
$$f'(t)\times f^{\prime\prime}(t)\cdot f^{\prime\prime\prime}(t)=(ab\sin(t),-ab\cos(t),a^{2})\cdot (a\sin(t),-a\cos(t),0)=a^{2}b$$
$$\|f'(t)\times f»(t)\|=\|(ab\sin(t),-ab\cos(t),a^{2})\|=\sqrt{a^{2}b^{2}+a^{4}}=|a|\sqrt{a^{2}+b^{2}}$$
luego,
$$\tau(t)=\frac{[f'(t)\times f^{\prime\prime}(t)]\cdot f^{\prime\prime\prime}(t)}{\|f'(t)\times f^{\prime\prime}(t)\|^{2}}=\frac{a^{2}b}{\left(|a|\sqrt{a^{2}+b^{2}}\right)^{2}}=\frac{b}{a^{2}+b^{2}}.~~ \blacksquare$$

Más adelante

En la siguiente entrada veremos cómo las curvaturas de las ecuaciones polares determinadas por los vectores tangente, normal y binormal dan origen a las fórmulas de Frenet-Serret. En la geometría de las curvas dichas fórmulas juegan un papel importante.

Tarea Moral

1.- Determine la curvatura de la parábola: $y=4px^2$

2.- Demuestra que $N´=-kl´T´+tl’B$

3.- Determina la torsión de la cúbica descrita por $f(t)=(t,t^2,t^3)$

4.-Determina la torsión de la hélice cónica descrita por $f(t)=(tcost, tsent, t)$ en el punto $(0,0,0)$.

5.- Determina la torsión de la curva descrita por $f(t)=(t-sent, 1-cost,t)$ en los puntos: $t=0$, $t=\dfrac{\pi}{2}$, $t=\pi$