MATERIAL EN REVISIÓN

Introducción

En las secciones pasadas comentamos que existen conjuntos con comportamientos muy «patológicos» respecto a la medida exterior. Vimos ejemplos donde la aditivad no se satisface, una propiedad deseable en cualquier noción de medida. Una posible manera de arreglar este problema es, en vez de buscar definir la medida sobre todos los subconjuntos de ${\mathbb{R}}^n$, restringirnos únicamente a los «conjuntos bien portados» respecto a la medida exterior (esperando que esta clase de conjuntos sea lo suficientemente general). Ésta es precisamente la idea de conjunto medible.

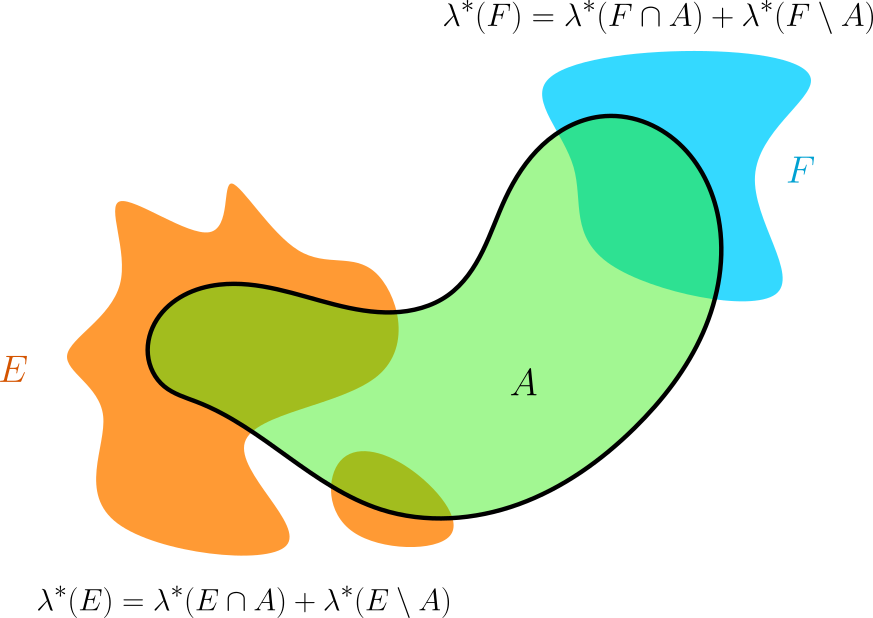
Definición. Sea $A$ un subconjunto de ${\mathbb{R}}^n$. Decimos que $A$ es Lebesgue medible o simplemente medible si y sólo si para cualquier $E\subseteq {\mathbb{R}}^n$,
$${\lambda }^{\ast }(E)={\lambda }^{\ast }(E\cap A)+{\lambda }^{\ast }(E\setminus A)$$ Si $A$ es medible, definimos su medida de Lebesgue, $\lambda (A)$, como su medida exterior: $$\lambda (A)={\lambda }^{\ast }(A).$$

Es conveniente pensar a los conjuntos medibles como aquellos «bien portados» bajo la aditividad.

Existen varias definiciones equivalentes de conjuntos medibles. Más adelante veremos algunas de ellas.

Observación. Recordando que $E\setminus A=E\cap A^c$, la igualdad en la definición de conjunto medible se puede escribir de forma alternativa como $${\lambda }^{\ast }(E)={\lambda }^{\ast }(E\cap A)+{\lambda }^{\ast }(E\cap A^c).$$ Usaremos una u otra según convenga.

Observación. Para probar que un conjunto $A$ es medible, hay que probar que ${\lambda }^{\ast }(E)={\lambda }^{\ast }(E\cap A)+{\lambda }^{\ast }(E\setminus A)$ para cualquier $E\subseteq {\mathbb{R}}^n$. Observa que, por subaditividad, siempre es cierto que ${\lambda }^{\ast }(E)\le {\lambda }^{\ast }(E\cap A)+{\lambda }^{\ast }(E\setminus A)$. Así que es suficiente probar la desigualdad opuesta. Más aún, si $E$ es de medida exterior infinita, dicha desigualdad se da de manera trivial, por tanto, basta suponer que $E$ es de medida exterior finita. En resúmen $A$ es medible si y sólo si para cualquier $E$ con ${\lambda }^{\ast }(E)<\mathrm{\infty }$, se satisface $${\lambda }^{\ast }(E\cap A)+{\lambda }^{\ast }(E\setminus A)\le {\lambda }^{\ast }(E).$$

No es inmediato ver que siquiera existen conjuntos medibles. Veremos primero dos ejemplos sencillos pero muy importantes. Más adelante probaremos que la clase de conjuntos medibles es cerrada bajo una gran cantidad de operaciones con conjuntos (complementos, uniones e intersecciones finitas y numerables, entre otros) lo que garantizará que la clase de conjuntos medibles es de hecho bastante general.

Dos ejemplos importantes de conjuntos medibles.

Definición. Decimos que un conjunto $N\subseteq {\mathbb{R}}^n$ es nulo si tiene medida exterior cero.

Proposición. Los conjuntos nulos son medibles.

Demostración. Sea $N\subseteq {\mathbb{R}}^n$ un conjunto con ${\lambda }^{\ast }(N)=0$ y $E\subseteq {\mathbb{R}}^n$ un conjunto arbitrario. Por subaditividad ya sabemos que ${\lambda }^{\ast }(E)\le {\lambda }^{\ast }(E\cap N)+{\lambda }^{\ast }(E\setminus N)$ así que basta probar la desigualdad opuesta.

Por monotonía tenemos $0\le {\lambda }^{\ast }(N\cap E)=\le {\lambda }^{\ast }(N)=0$ y ${\lambda }^{\ast }(E\setminus N)\le {\lambda }^{\ast }(E)$ , luego:
$${\lambda }^{\ast }(E\cap N)+{\lambda }^{\ast }(E\setminus N)=0+{\lambda }^{\ast }(E\setminus N)\le {\lambda }^{\ast }(E)$$ Como lo anterior es cierto para cualquier $E\subseteq {\mathbb{R}}^n$, concluimos que $N$ es medible.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Proposición. Los semiespacios, es decir, conjuntos de la forma $$H_i^{\pm }=\{(x_1,x_2,\dots ,x_n)\in {\mathbb{R}}^n:\pm x_i\ge 0\}$$ Son medibles.

Demostración. Probaremos que $H_1^{+}$ es medible. Los demás casos son idénticos. Como ya observamos, es suficiente probar que ${\lambda }^{\ast }(E\cap A)+{\lambda }^{\ast }(E\setminus A)\le {\lambda }^{\ast }(E)$ para cualquier $E$ con ${\lambda }^{\ast }(E)<\mathrm{\infty }$.

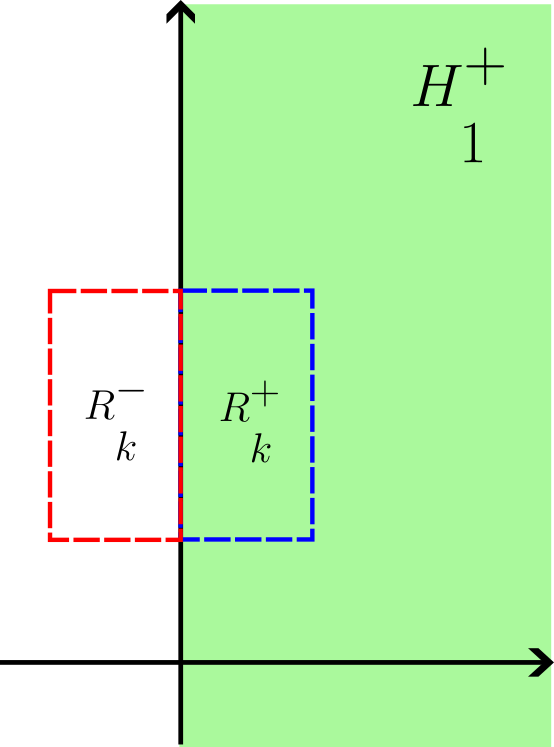
Sea entonces $E\subseteq {\mathbb{R}}^n$ con ${\lambda }^{\ast }(E)<\mathrm{\infty }$ arbitrario. Dado $\epsilon >0$ arbitrario, tomemos una cubierta con rectángulos cerrados $E\subseteq \bigcup _{k=1}^{\mathrm{\infty }}{R}_k$ tal que $${\lambda }^{\ast }(E)\le \sum _{k=1}^{\mathrm{\infty }}|R_k|<{\lambda }^{\ast }(E)+\epsilon .$$ Si hay algún rectángulo «partido» por el semiespacio, es decir, $R_k=[a_1^k,b_1^k]\times [a_2^k,b_2^k]\times \cdots \times [a_n^k,b_n^k].$ Con $a_1^k<0<b_1^k$, podemos reemplazarlo por los dos subrectángulos $R_k^{-}=[a_1^k,0]\times [a_2^k,b_2^k]\times \cdots \times [a_n^k,b_n^k]$ y $R_k^{+}=[0,b_1^k]\times [a_2^k,b_2^k]\times \cdots \times [a_n^k,b_n^k]$ como en la figura (nota que $|R_k|=|R_k^{+}|+|R_k^{-}|$). Así que podemos suponer sin pérdidad de generalidad que para cualquier $k=1,2,\dots$, o bien $R_k\subseteq H_1^{+}$ o bien $R_k\subseteq H_1^{-}$.

Si denotamos por $I^{+}$ al conjunto de índices $k$ tales que $R_k\subseteq H_1^{+}$ y por $I^{-}$ al conjunto de índices $k$ tales que $R_k\cap (H_1^{+}{)}^c\ne \mathrm{\varnothing }$, claramente:
$$E\cap H_1^{+}\subseteq \bigcup _{k\in I^{+}}{R}_k;E\setminus H_1^{+}\subseteq \bigcup _{k\in I^{-}}{R}_k$$ De donde:
$$\begin{array}{rl}{\lambda }^{\ast }(E\cap H_1^{+})+{\lambda }^{\ast }(E\setminus H_1^{+})& \le \sum _{k\in I^{+}}|R_k|+\sum _{j\in I^{-}}|R_j|\\ & \le \sum _{k=1}^{\mathrm{\infty }}|R_k|\\ & <{\lambda }^{\ast }(E)+\epsilon \end{array}$$

Como esto es cierto para cualquier $\epsilon >0$, necesariamente $${\lambda }^{\ast }(E\cap H_1^{+})+{\lambda }^{\ast }(E\setminus H_1^{+})\le {\lambda }^{\ast }(E).$$

Concluimos que $H_1^{+}$ es un conjunto medible.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Conjuntos medibles y operaciones con conjuntos

Veamos que la clase de conjuntos medibles es cerrada bajo operaciones «básicas» con conjuntos. Más adelante veremos algunos resultados más fuertes.

Proposición (Propiedades de conjuntos medibles).

1. Si $A$ es medible, entonces su complemento $A^c={\mathbb{R}}^n\setminus A$ es medible.
2. Si $A$ es medible y $x\in {\mathbb{R}}^n$, entonces la traslación $x+A$ es medible.
3. Si $A_1,A_2,\dots A_m$ son medibles, entonces $\bigcup _{k=1}^m{A}_k$ y $\bigcap _{k=1}^m{A}_k$ son medibles.

Demostración. 1. es inmediato gracias a la simetría de la definición.

Por un argumento de doble contención es fácil verificar que para cualquier $E\subseteq {\mathbb{R}}^n$, $$E\cap (x+A)=x+((-x+E)\cap A)$$ Y $$E\setminus (x+A)=x+((-x+E)\setminus A).$$ Usando la invarianza bajo traslaciones de la medida exterior y el hecho de que $A$ es medible:

$$\begin{array}{rl}{\lambda }^{\ast }(E)& ={\lambda }^{\ast }(-x+E)\\ & ={\lambda }^{\ast }((-x+E)\cap A)+{\lambda }^{\ast }((-x+E)\setminus A)\\ & ={\lambda }^{\ast }(x+(-x+E)\cap A)+{\lambda }^{\ast }(x+(-x+E)\setminus A)\\ & ={\lambda }^{\ast }(E\cap (x+A))+{\lambda }^{\ast }(E\setminus (x+A)).\end{array}$$ Se sigue 2.

Probaremos 3. para el caso en el que tenemos solamente dos conjuntos. El caso general se sigue fácilmente por inducción. Sean entonces $A$ y $B$ conjuntos medibles y $E\subseteq {\mathbb{R}}^n$ cualquier conjunto con medida exterior finita. Usando la definición sobre $A$, $B$, y las leyes de De Morgan:

$$\begin{array}{rl}{\lambda }^{\ast }(E)& ={\lambda }^{\ast }(E\cap A)+{\lambda }^{\ast }(E\cap A^c)\\ & ={\lambda }^{\ast }((E\cap A)\cap B)+{\lambda }^{\ast }((E\cap A)\cap B^c)+{\lambda }^{\ast }((E\cap A^c)\cap B)+{\lambda }^{\ast }((E\cap A^c)\cap B^c)\\ & ={\lambda }^{\ast }(E\cap A\cap B)+{\lambda }^{\ast }(E\cap A\cap B^c)+{\lambda }^{\ast }(E\cap A^c\cap B)+{\lambda }^{\ast }(E\cap (A\cup B{)}^c).\end{array}$$

Por otro lado, como $A\cup B=(A\cap B)\cup (A\cap B^c)\cup (A^c\cap B)$, tenemos por subaditividad:
$${\lambda }^{\ast }(E\cap (A\cup B))\le {\lambda }^{\ast }(E\cap (A\cap B))+{\lambda }^{\ast }(E\cap (A\cap B^c))+{\lambda }^{\ast }(E\cap (A^c\cap B)).$$
Finalmente, usando las desigualdades anteriores tenemos:

$$\begin{array}{rl}& {\lambda }^{\ast }(E\cap (A\cup B))+{\lambda }^{\ast }(E\cap (A\cup B{)}^c)\\ & \le {\lambda }^{\ast }(E\cap (A\cap B))+{\lambda }^{\ast }(E\cap (A\cap B^c))+{\lambda }^{\ast }(E\cap (A^c\cap B))+{\lambda }^{\ast }(E\cap A^c\cap B^c)\\ & ={\lambda }^{\ast }(E).\end{array}$$
Concluimos (por la observación) que $A\cup B$ es un conjunto medible. Para el caso de la intersección simplemente observamos que: $A\cap B=(A^c\cup B^c{)}^c$. Éste último siendo medible por las propiedades anteriores.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

La proposición anterior nos asegura que la clase de conjuntos medibles es cerrada bajo operaciones básicas con conjuntos, más adelante veremos versiones más fuertes de estos resultados. Ahora estamos en condiciones de dar un par de ejemplos esperables de conjuntos medibles, además de algunos resultados relacionados con la aditividad.

Corolario. Los rectángulos cerrados y abiertos son conjuntos medibles.
Demostración. Los rectángulos cerrados se pueden ver como una intersección finita de semiespacios trasladados. Los rectángulos abiertos se pueden ver como una intersección finita de complementos de semiespacios cerrados (es decir «semiespacios» abiertos).

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Veamos ahora que la medida de Lebesgue sobre los conjuntos medibles es aditiva. Una de las grandes ventajas de este concepto.

Proposición (Aditividad de la Medida de Lebesgue).

1. Si $A_1,A_2,\dots ,A_n$ son conjuntos medibles ajenos dos a dos, entonces $$\lambda (\bigcup _{k=1}^n{A}_k)=\sum _{k=1}^n\lambda (A_k).$$
2. Si $B\subseteq A$ y $B$ es de medida finita entonces $$\lambda (A\setminus B)=\lambda (A)-\lambda (B).$$

Demostración. Por las proposiciones anteriores, todos los conjuntos en cuestión son medibles, así que tiene sentido hablar de su medida de Lebesgue.

Probaremos 1. solamente para dos conjuntos ajenos. El caso general se sigue por inducción. Para ello simplemente notemos que:
$$\begin{array}{rl}\lambda (A\cup B)& ={\lambda }^{\ast }(A\cup B)\\ & ={\lambda }^{\ast }((A\cup B)\cap A)+{\lambda }^{\ast }((A\cup B)\cap A^c)\\ & ={\lambda }^{\ast }(A)+{\lambda }^{\ast }(B)\\ & =\lambda (A)+\lambda (B).\end{array}$$
En la segunda igualdad se usó la definición de que $A$ es medible.

Para 2. notemos que $A$ es la unión ajena de $B$ y $A\setminus B$. Se sigue por el inciso anterior que
$$\lambda (A)=\lambda (B)+\lambda (A\setminus B)$$ $$⟹\lambda (A\setminus B)=\lambda (A)-\lambda (B).$$
(La restricción de que $B$ sea de medida finita es simplemente para que la expresión $\lambda (A)-\lambda (B)$ tenga sentido).

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Más adelante…

Seguiremos con nuestro estudio de los conjuntos medibles. Veremos que los conjuntos medibles son cerrados bajo otras operaciones con conjuntos (por ejemplo uniones numerables), lo que nos permitirá probar que la clase de conjuntos medibles es de hecho bastante general.

Tarea moral

• Prueba que si $A,B$ son conjunto medibles, entonces $A\setminus B$ es un conjunto medible.