$\framebox[5cm][c]{Medida de Jordan}$
$\textcolor{Blue}{Definición}$
Dado $A\subset \mathbb{R}^{n}$ acotado, definimos $\chi_{A}:\mathbb{R}^{n}\rightarrow \mathbb{R}$, la $\textcolor{Red}{función~ característica}$ de A, de la siguiente forma
$$\boxed{\chi_{A}=\left\{\begin{matrix}
1&si&x\in A\\0&si& x\notin A\end{matrix}\right.}$$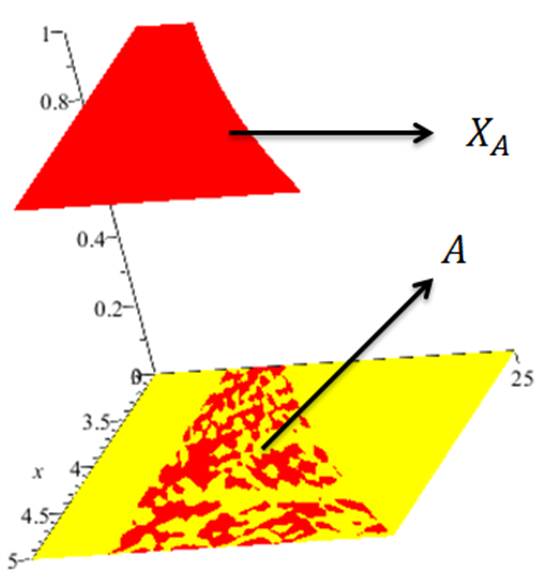

Dado $A\subset \mathbb{R}^{n}$ acotado, decimos que A es $\textcolor{Red}{Jordan Medible} si la función característica de A es integrable sobre algún rectángulo R que contenga a A. En este caso decimos que la medida de Jordan de A (que denotaremos J(A)) esta dada por
$$\boxed{J(A)=\int_{R}\chi_{A}}$$
$\textcolor{Green}{Ejemplo:}$
Sean a,b números positivos y $$A=\left\{(x,y)\in \mathbb{R}^{2}| 0\leq x\leq a, 0\leq y \leq \left(\frac{b}{a}x\right)\right\}$$ En este caso A es un triángulo de base a y altura b. Mostraremos que A es Jordan-Medible en $\mathbb{R}^{2}$, y que su medida es $\frac{ab}{2}$
$\textcolor{Green}{Demostración:}$
Tomemos el rectángulo $R=\{(x,y)\in \mathbb{R}^{2}|0\leq x\leq a, 0\leq y \leq b\}=[0,a]\times[0,b]$ el cual contiene a A. De acuerdo con nuestra definición tenemos que mostar que la función característica $\chi_{A}$ es integrable sobre R y que $$\boxed{\int_{R}\chi_{A}=\frac{ab}{2}}$$
Sea $\displaystyle{P_{1}=\left\{\frac{ia}{n}~|~i=1,…,n\right\}}$ y $\displaystyle{P_{2}=\left\{\frac{ib}{n}~|~i=1,…,n\right\}}$ por tanto $P=P_{1}\times P_{2}$ es una partición del rectángulo R, donde cada subrectángulo tiene medida $\displaystyle{\frac{ab}{n^{2}}}$. Por lo que en este caso
$$\overline{S}(\chi_{A},P)=\sum_{R_{i}\cap A\neq \emptyset}=2\cdot \frac{ab}{n^{2}}+3\cdot \frac{ab}{n^{2}}+…+n\cdot \frac{ab}{n^{2}}=\frac{ab}{n^{2}}\left(\frac{n(n+1)}{2}-1\right)=\frac{ab}{2}\left(1+\frac{1}{n}-\frac{1}{n^2}\right)$$
$$\underline{S}(\chi_{A},P)=\sum_{R_{i}\subset A\neq \emptyset}=1\cdot \frac{ab}{n^{2}}+2\cdot \frac{ab}{n^{2}}+…+(n-1)\cdot \frac{ab}{n^{2}}=\frac{ab}{n^{2}}\left(\frac{(n-1)n}{2}\right)=\frac{ab}{2}\left(1-\frac{1}{n}\right)$$
$\therefore$
$$\lim_{n\rightarrow \infty}\overline{S}(\chi_{A},P)=\lim_{n\rightarrow \infty}\underline{S}(\chi_{A},P)=\frac{ab}{2}$$
$$\boxed{J(A)=\int_{R}\chi_{A}=\frac{ab}{2}}$$

$\textcolor{Green}{Ejemplo:}$
Sea A el conjunto $$A=\left\{(x,y)\in \mathbb{R}^{2}~|~ 0\leq x\leq 1, 0\leq y \leq x^{2}\right\}$$ En este caso A la región de base 1 y altura la función $x^{2}$. Mostraremos que A es Jordan-Medible en $\mathbb{R}^{2}$, y que su medida es $\displaystyle{\frac{1}{3}}$
$\textcolor{Green}{Demostración:}$
Tomemos el rectángulo $R=\{(x,y)\in \mathbb{R}^{2}|0\leq x\leq 1, 0\leq y \leq 1\}=[0,1]\times[0,1]$ el cual contiene a A. De acuerdo con nuestra definición tenemos que mostar que la función característica $\chi_{A}$ es integrable sobre R y que $$\boxed{\int_{R}\chi_{A}=\frac{1}{3}}$$
Sea $\displaystyle{P_{1}=\left\{\frac{ia}{n}~|~i=1,…,n\right\}}$ y $\displaystyle{P_{2}=\left\{\frac{ib}{n}~|~i=1,…,n\right\}}$ por tanto $P=P_{1}\times P_{2}$ es una partición del rectángulo R, donde cada subrectángulo tiene medida $\displaystyle{\frac{1}{n^{2}}}$. Por lo que en este caso
$$\overline{S}(\chi_{A},P)=\sum_{R_{i}\cap A\neq \emptyset}=\frac{1}{n}\cdot \frac{1}{n^{2}}+\frac{1}{n}\cdot \frac{2^{2}}{n^{2}}+…+\frac{1}{n}\cdot \frac{n^{2}}{n^{2}}=\frac{1}{n^{3}}\left(1+2^{2}+\cdots+n^{2}\right)=\frac{1}{n^{3}}\left(\frac{n(n+1)(2n+1)}{6}\right)=\frac{1}{6}\left(1+\frac{1}{n}\right)\left(1+\frac{1}{n}\right)$$
$$\underline{S}(\chi_{A},P)=\sum_{R_{i}\subset A\neq \emptyset}=\frac{1}{n}\cdot \frac{1}{n^{2}}+\frac{1}{n}\cdot \frac{2^{2}}{n^{2}}+…+\frac{1}{n}\cdot \frac{(n-1)^{2}}{n^{2}}=\frac{1}{n^{3}}\left(1+2^{2}+\cdots+(n-1)^{2}\right)=\frac{1}{n^{3}}\left(\frac{(n-1)n(2(n-1)+1)}{6}\right)$$
$$=\frac{1}{6}\left(1-\frac{1}{n}\right)\left(2-\frac{1}{n}\right)$$
$\therefore$
$$\lim_{n\rightarrow \infty}\overline{S}(\chi_{A},P)=\lim_{n\rightarrow \infty}\underline{S}(\chi_{A},P)=\frac{1}{3}$$
$$\boxed{J(A)=\int_{R}\chi_{A}=\frac{1}{3}}$$

$\textcolor{Blue}{Teorema}$
Sea $A\subset\mathbb{R}^{n}$ acotado. Las siguientes afirmaciones son equivalentes:
1.- A es Jordan-Medible
2.-Para cada $\epsilon>0$ existen $R_{1},…,R_{k}$ rectángulos tales que:
(a) $Fr(A)\subset R_{1}\cup\cdots\cup R_{k}$
(b) $\displaystyle{\sum_{i=1}^{k}m(R_{i})<\epsilon}$
3.-La $Fr(A)$ es Jordan-Medible y $J(Fr(A))=0$
$\textcolor{Blue}{Demostración:}$
$(1)\Rightarrow (2)$
Sea $\epsilon>0$. Como A es Jordan-Medible, sabemos que $\chi_{A}$ es integrable sobre un rectángulo que contiene $\overline{A}$ por lo que existe una partición P de R tal que
$$\overline{S}(\chi_{A},P)-\underline{S}(\chi_{A},P)<\epsilon$$
en este caso
$$\overline{S}(\chi_{A},P)=\sum_{R_{i}\cap A\neq0}m(R_{i})$$
$$\underline{S}(\chi_{A},P)=\sum_{R_{i}\subset A}m(R_{i})$$
Por lo que
$$\overline{S}(\chi_{A},P)-\underline{S}(\chi_{A},P)=\sum_{R_{i}\cap A\neq \emptyset\atop{R_{i}\cap A^{c}\neq \emptyset}}m(R_{i})$$
Para ver que
$$Fr(A)\subset R_{1}\bigcup\cdots\bigcup R_{k}$$
Como $\underline{A}\subset int(R)$ entonces $Fr(A)\subset int(R)$. Sea $x\in Fr(A)$, si $x\in int(R_{i})$ entonces la condición se cumple
Si $x\notin int(R)$ entonces esta en la frontera de más de uno de los subrectángulos por lo que
(1) Si los subrectángulos estan en $int(A)$ entonces $x\in int(A)$
(2) Si los subrectángulos estan en $int(A^{c})$ entonces $x\in ext(A)$
En ambas situaciones $x\notin Fr(A)$ lo cual es una contradicción.
Por lo tanto $x\in R_{i}$ donde $R_{i}$ cumple la condición pedida.
$(2)\Rightarrow (3)$
Para probar que $Fr(A)$ es Jordan-Medible, se tiene que probar que $\chi_{A}$ es integrable sobre el rectángulo R ya que $Fr(a)\subset R$.
Como existen $R_{1},…,R_{k}$ rectángulos tales que:
\begin{align*}
(a)&Fr(A)\subset R_{1}\bigcap\cdots\bigcap R_{k}\\
(b)&\sum_{i=1}^{k}m(R_{i})<\epsilon
\end{align*}
Entonces
$$\overline{S}(\chi_{Fr(A)},P)=\sum_{R_{i}\cap A\neq\emptyset\atop{R_{i}\cap A^{c}\neq\emptyset}}m(R_{i})<\epsilon$$
Y como
$$\underline{S}(\chi_{Fr(A)},P)\leq \overline{S}(\chi_{Fr(A)},P)<\epsilon$$
entonces
$$0\leq \sup\{\underline{S}(\chi_{Fr(A)},P)\}<\epsilon$$
$$0\leq \inf\{\overline{S}(\chi_{Fr(A)},P)\}<\epsilon$$
entonces
$$\int_{R}\chi_{Fr(a)}=\overline{\int}_{R}\chi_{Fr(A)}=\underline{\int}_{R}\chi_{Fr(A)}=0$$
$(3)\Rightarrow (1)$
Como $Fr(A)$ es Jordan-Medible y $J(Fr(A))=0$, existe una partición P tal que $Fr(A)\cap R_{i}\neq\emptyset$ entonces
$$\overline{S}(\chi_{Fr(A)})=\sum_{R_{i}\cap Fr(A)\neq \emptyset}m(R_{i})<\epsilon$$
Por lo tanto
$$\overline{S}(\chi_{Fr(A)})-\underline{S}(\chi_{Fr(A)})=\sum_{R_{i}\cup A\neq\emptyset\atop{R_{i}\cup A^{c}\neq\emptyset}}m(R_{i})\leq \sum_{R_{i}\cup Fr(A)\neq\emptyset}m(R_{i})<\epsilon$$
por lo tanto $\chi_{A}$ es integrable sobre R y en consecuencia A es un conjunto Jordan-Medible.$~~\blacksquare$

$\textcolor{Blue}{Teorema}$
Sea $f:R\subset\mathbb{R}\rightarrow\mathbb{R}$ acotada sobre el rectángulo R. Si el conjunto de discontinuidades de f en R $(D_{f,R})$ es un conjunto Jordan-Medible y de Medida cero entonces f es integrable sobre R.
$\textcolor{Blue}{Demostración}$
Sea $M>0$ tal que $|f(\widehat{x})|\leq M$ para todo $\widehat{x}\in R$.
Sea $\epsilon>0$. Dado que $J(D_{f,R})=0$ sabemos que existe una partición P de R tal que
$$\overline{S}(\chi_{D_{f,R}},P)<\frac{\epsilon}{4M}$$
Si $R_{1},…,R_{l}$ son los subrectángulos de R inducidos por la partición P que tienen la propiedad de que $R_{i}\cap D_{f,R}\neq\emptyset~~(i=1,2,…,l)$, tenemos entonces que
$$\sum_{i=1}^{l}m(R_{i})<\frac{\epsilon}{4M}$$
Si $R_{\ell+1},…,R_{k}$ son el resto de los subrectángulos de R inducidos por P, sabemos que f es continua en cada uno de ellos por tanto f es integrable sobre cada $R_{i}~~(i=\ell+1,…,k)$. Para cada uno de estos subrectángulos podemos encontrar una partición $P^{(i)}$ tal que
$$\overline{S}(f,P^{(i)})-\underline{S}(f,P^{(i)})<\frac{\epsilon}{2(k-\ell)}$$
Para cada $i=\ell+1,…,k$. Cada una de estas particiones $P^{(i)}$ la extendemos a todo el rectángulo R y junto con la partición inicial P, formamos una nueva partición del rectángulo R a la que llamaremos Q.
si los subrectángulos inducidos por Q los denotamos $R^{‘}_{j,i}$, en donde $(i=1,…,k)$ y $(j=1,..k_{i})$, entonces
$$R_{i}=\bigcup_{j=1}^{k_{i}}R’_{j,i}$$
Observe que para $i=\ell+1,…,k$ los $R’_{j,i}$ $(j=1,…,k_{i})$ son subrectángulo de $R_{i}$ inducidos por alguna partición $Q^{(i)}$ que refina a $P^{(i)}$ de modo tal que
\begin{align*}
\overline{S}(f,Q^{(i)})-\underline{S}(f,Q^{i})&\leq \overline{S}(f,P^{(i)})-\underline{S}(f,P^{i})\\
&<\frac{\epsilon}{2(k-\ell)}
\end{align*}
Tenemos que
\begin{align*}
\overline{S}(f,Q)-\underline{S}(f,Q)&=\sum_{i=1}^{k}\left(\sum_{j=1}^{k}(M’_{j,i}-m’_{j,i})\cdot m(R’_{j,i}\right)\\
&=\sum_{i=1}^{k}\left(\sum_{j=1}^{k}(M’_{j,i}-m’_{j,i})\cdot m(R’_{j,k}\right)+\sum_{i=\ell+1}^{k}\left(\sum_{j=1}^{k}(M’_{j,i}-m’_{j,i})\cdot m(R’_{j,k}\right)\\
&=\sum_{i=1}^{\ell}\left(\sum_{j=1}^{k_{i}}(M’_{j,i}-m’_{j,i})\cdot m(R’_{j,k}\right)+\sum_{i=\ell+1}^{k}\left(\overline{S}(f,Q^{i})-\underline{S}(f,Q^{i})\right)\\
&\leq \sum_{i=1}^{\ell}\left(\sum_{j=1}^{k_{i}}2M\cdot m(R’_{j,i})\right)+\sum_{i=\ell+1}^{k}\left(\overline{S}(f,P^{i})-\underline{S}(f,P^{i})\right)\\
&<2M\cdot \sum_{i=1}^{\ell}\left(\sum_{j=1}^{k_{i}} m(R’_{j,i})\right)+\sum_{i=\ell+1}^{k}\frac{\epsilon}{2(k-\ell)}\\
&=2M\cdot \sum_{i=1}^{\ell}m(R_{i})+\frac{\epsilon}{2}\\
&<2M\cdot \left(\frac{\epsilon}{4M}\right)+\frac{\epsilon}{2}\\
&=\epsilon
\end{align*}
En donde, como era de esperarse, $M’_{j,i}=\sup\{f(\widehat{x})~|~\widehat{x}\in R’_{j,i}\}$ y $m’_{j,i}=\inf\{f(\widehat{x})~|~\widehat{x}\in R’_{j,i}\}$ para $i=1,…,k$ y $j=1,…,k_{i}$.$~~\blacksquare$