Si $f:A\subset\mathbb{R}^{2}\rightarrow \mathbb{R}$. Denotamos por $D_{fA}$ al conjunto de discontinuidades de f en A, es decir
$$D_{fA}=\{x\in A~|~f~es~discontinua~en~x\}$$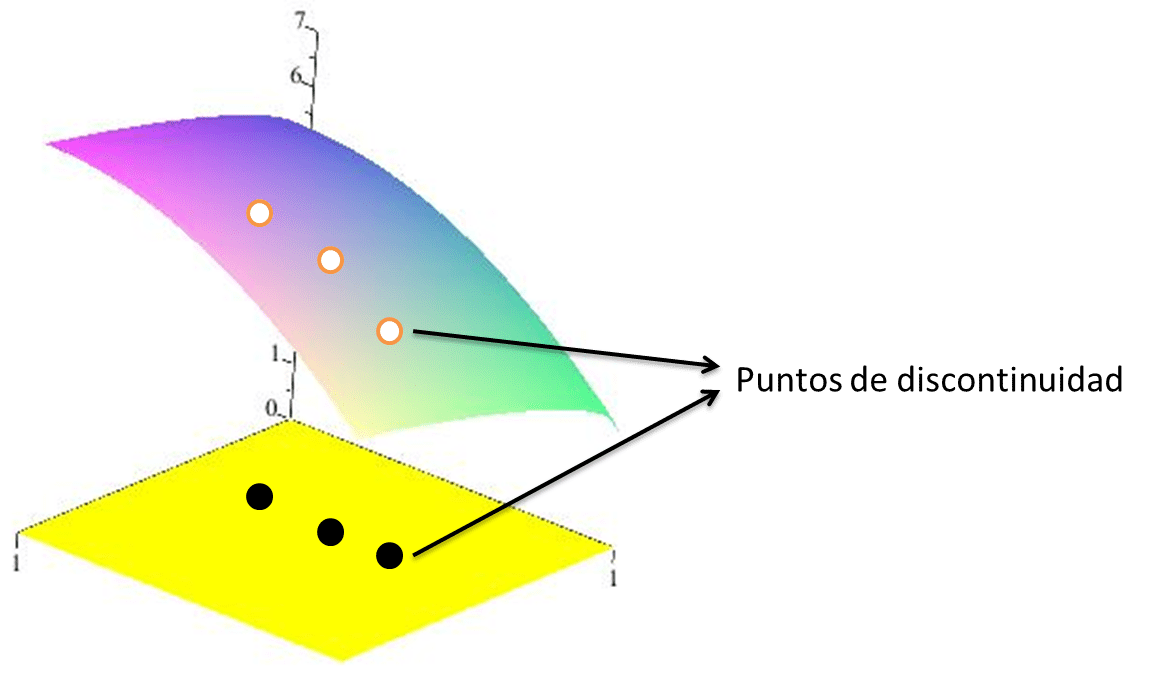

$\textcolor{Blue}{Proposición}$: Sea $f:A\subset\mathbb{R}^{2}\rightarrow \mathbb{R}$ integrable sobre R. Entonces $D_{fR}$ tiene interior vacio $int~D_{fR}=\emptyset$
$\textcolor{Blue}{Demostración}$: Si $int~D_{fR}\neq\emptyset$ entonces existe $R’$ tal que $R’\subset int(D_{fR})\subset D_{fR}\subset R$
como f es integrable sobre R y $R’\subset R$ entonces f es integrable sobre $R’$ de modo que existe $x_{0}\in int(R’)$ tal que f es continua en $x_{0}$ lo cual contradice el hecho de que f es discontinua en todo $x\in D_{fR}$.$~~\blacksquare$

Medida Cero y Contenido Cero
$\textcolor{Blue}{Definición}$: Un subconjunto $A\subset\mathbb{R}^{n}$ tiene medida cero si para cada $\epsilon>0$ existe un recubrimiento ${U_{1},U_{2},…}$ de A por rectángulos tales que
$$A\subset \bigcup_{i=1}^{\infty}U_{i}~~y~~\sum_{i=1}^{\infty}v(U_{i})<\epsilon$$
Por ejemplo un conjunto formado por un número finito de puntos claramente tiene medida cero

Si A tiene infinitos puntos que pueden ordenarse formando una sucesión $a_{1},a_{2},…$ entonces A tiene medida cero, pues para cada $\epsilon>0$ se puede elegir $U_{i}$ que sea rectángulo cerrado que contenga $a_{i}$ con $\displaystyle{v(U_{i})<\frac{\epsilon}{2^{i}}}$.
Entonces$$\sum_{i=1}^{\infty}v(U_{i})<\sum_{i=1}^{\infty}\frac{\epsilon}{2^{i}}=\epsilon\sum_{i=1}^{\infty}\frac{1}{2^{i}}=\epsilon\left(\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+…\right)=\frac{\epsilon}{2}\left(1+\frac{1}{2}+…\right)=$$
$$\frac{\epsilon}{2}\left(\frac{1}{1-\frac{1}{2}}\right)=\frac{\epsilon}{2}(2)=\epsilon$$

$\textcolor{Green}{Ejemplo}$: $\mathbb{Q}$ es de medida cero.
$\textcolor{Green}{Demostración}$: Como $\mathbb{Q}$ es numerable podemos formar $\displaystyle{\left\{r_{k}\right\}^{\infty}_{1}}$ y dado $\epsilon>0$, sea $$I_{k}=\left(r_{k}-\frac{\epsilon}{2^{k+2}},r_{k}+\frac{\epsilon}{2^{k+2}}\right)$$Por lo que $$\mathbb{Q}\subset \bigcup_{k=1}^{\infty} I_{k}\quad y \quad v(I_{k})=\frac{\epsilon}{2^{k+1}}$$y para la suma de los volumenes se tiene
$$\sum_{k=1}^{\infty}\frac{\epsilon}{2^{k+1}}=\frac{\epsilon}{4}\left(1+\frac{1}{2}+…\right)=\frac{\epsilon}{2}<\epsilon$$
$\therefore$ $\mathbb{Q}$ tiene medida cero.$~~\blacksquare$

$\textcolor{Green}{Ejemplo}$: El conjunto de Cantor
$\textcolor{Green}{Demostración}$: Tenemos que
\begin{align} \mathcal{C}_{0} &=[0,1]\\ \mathcal{C}_{1}&= \left[0,\frac{1}{3}\right] \cup \left[\frac{2}{3},1\right]\\ \mathcal{C}_{2}&= \left[0,\frac{1}{9}\right] \cup \left[\frac{2}{9},\frac{1}{3}\right]\cup \left[\frac{2}{3},\frac{7}{9}\right]\ \cdot\ \cdot\ \cdot\ \mathcal{C}{n}=\left[0,\frac{1}{3^{n}}\right]\cup \cdot \cdot \cdot \cup \left[1-\frac{1}{3^{n}},1\right]
\end{align}
Tenemos que $\displaystyle{\mathcal{C}=\bigcap_{k=0}^{\infty}\mathcal{C}_{k}}$ (Conjunto de Cantor).
Cada $\mathcal{C}_{k}$ es la unión de $2^{k}$ intervalos de longitud $\displaystyle{\frac{1}{3^{k}}}$ si los llamamos $I{1}, I_{2},…,I_{2^{k}}$ entonces
$$\mathcal{C}\subset \mathcal{C}_{k}=\bigcup{i=1}^{2^{k}}I_{i} \quad y \quad \sum_{i=1}^{2^{k}}vol(I_{i})=\left(\frac{2}{3}\right)^{k}$$
por lo que dado $\epsilon>0$ podemos tomar $k$ tal que $\displaystyle{\left(\frac{2}{3}\right)^{k}<\epsilon}$. Entonces $\mathcal{C}$ es de medida cero.$\blacksquare$

$\textcolor{Green}{Ejemplo}$: En $\mathbb{R}^{2}$ consideramos la recta $y=y_{0}$
$\textcolor{Green}{Demostración}: La semirecta derecha $A={(x,y_{0})| x\in \mathbb{R}}$ la cubrimos con $$R_{k}=\left[k,k+1\right]\times \left[y_{0}-\frac{\epsilon}{2^{k+3}},y_{0}+\frac{\epsilon}{2^{k+3}}\right]$$ con $k\in \mathbb{N}\cup {0}$ y $$v(R_{k})=1\cdot \left(\frac{\epsilon}{2^{k+2}}\right)\Rightarrow \sum_{k=1}^{\infty}\frac{\epsilon}{2^{k+2}}=\frac{\epsilon}{2}<\epsilon$$
Mientras que para la semirecta izquierda consideramos $$R_{k}=\left[-k-1,-k\right]\times \left[y_{0}-\frac{\epsilon}{2^{k+3}},y_{0}+\frac{\epsilon}{2^{k+3}}\right]$$
$\therefore$
$$v(R_{k})=1\cdot \left(\frac{\epsilon}{2^{k+2}}\right)\Rightarrow \sum_{k=1}^{\infty}\frac{\epsilon}{2^{k+2}}=\frac{\epsilon}{2}<\epsilon$$
$\therefore$ la recta entera se puede cubrir con una unión numerable de rectángulos cuya suma es menor a $\epsilon$.$\blacksquare$

$\textcolor{Green}{Ejemplo}$: Los intervalos cerrados $[a,b]\subset \mathbb{R}$ con $a<b$ no tienen medida cero.
$\textcolor{Green}{Demostración}$: Supongamos que $[a,b]\subset \bigcup_{n=1}^{\infty}U_{n}$ con $U_{n}$ abierto, como $[a,b]$ es compacto existe una subcubierta finita ${U_{n}}$ con $$\sum_{k=1}^{\infty} v(U_{k})<\epsilon \quad pero \quad \sum_{k=1}^{\infty} v(U_{k})\geq b-a$$ lo cual nos dice que la suma de volumenes no se puede hacer tan pequeña como se desee, por lo que el conjunto dado no es de medida cero.$\blacksquare$

$\textcolor{Blue}{Teorema}$: Si $A=A_{1}\bigcup A_{2}\bigcup …$ y cada $A_{i}$
tiene medida cero, entonces A tiene medida cero.
$\textcolor{Blue}{Demostración}$: Sea $\epsilon>0$. Puesto que cada $A_{i}$ tiene medida cero
$\exists$ un recubrimiento ${U_{i1},U_{i2},…}$ de $A_{i}$ por
rectángulos cerrados tales que la colección de todos los $U_{ij}$
cubren a A y formamos la sucesión numerable $$U_{11},U_{1,2},…$$
$\therefore$
$$\sum_{j=1}^{\infty}v(U_{ij})<\sum_{i=1}^{\infty}\frac{\epsilon}{2^{i}}<\epsilon~\blacksquare$$

$\textcolor{Blue}{Definición}$: Un subconjunto A de $\mathbb{R}^{n}$ tiene contenido cero si para cada $\epsilon>0$ existe un recubrimiento finito ${U_{1},U_{2},…,U_{n}}$ de A por rectángulos tales que $$\sum_{i=1}^{n}v(U_{i})<\epsilon$$

$\textcolor{Blue}{Teorema}$: Si A es compacto y tiene medida cero, entonces A
tiene contenido cero.
$\textcolor{Blue}{Demostración}$: Sea $\epsilon>0$. Puesto que $A$ tiene medida cero,$\exists$ un recubrimiento ${U_{1},U_{2},…}$ de $A$ por rectángulos tales que $\displaystyle{\sum_{i=1}^{\infty}v(U_{i})<\epsilon}$. Dado que A es compacto, un
número finito de ${U_{1},U_{2},…,U_{n}}$ recubren a A y ademas
$\displaystyle{\sum_{i=1}^{n}v(U_{i})<\epsilon}~~\blacksquare$

$\textcolor{Blue}{Teorema}$: Sea $\phi:[a,b]\rightarrow\mathbb{R}$ una función continua. Entonces la gráfica de $\phi$ tiene contenido cero.
$\textcolor{Blue}{Demostración}$: Siendo $\phi$ continua en el compacto $[a,b]$, es
uniformemente continua en dicho intervalo. Es decir dado $\epsilon>0\quad\exists\quad\delta>0$ tal que para $x,y\in[a,b]$ si
$|x-y|<\delta\quad\Rightarrow\quad|f(x)-f(y)|<\frac{\epsilon}{b-a}$.
Sea $n\in\mathbb{N}$ tal que $\frac{b-a}{n}<\delta$ y consideremos
la partición de $[a,b]$ en n partes iguales
$$a=x_{0}<x_{1}<…<x_{n}=b$$ con $x_{i}=a+i\frac{b-a}{n}$ se tiene
entonces que para
$x,y\in[x_{i-1},x_{i}]\Rightarrow|f(x)-f(y)|<\frac{\epsilon}{b-a}$
$\therefore$
$$\sum_{i=1}^{n}(x_{i}-x_{i-1})\frac{\epsilon}{b-a}=\frac{\epsilon}{b-a}\sum_{i=1}^{n}(x_{i}-x_{i-1})=\frac{\epsilon}{b-a}(b-a)=\epsilon~~\blacksquare$$

$\textcolor{Blue}{Teorema}$: Sea R un rectángulo cerrado y $f:R\rightarrow
\mathbb{R}$ una función acotada. Sea $B=\{x\in\mathbb{R}|f\quad
no\quad es \quad continua\quad en\quad x\}$ entonces si B es un
conjunto de contenido cero f es integrable.
$\textcolor{Blue}{Demostración}$: Vamos a dividir los subrectángulos $R_{ij}$ en
$I)R_{ij}\bigcap B\neq\emptyset$ y $II)R_{ij}\bigcap B=\emptyset$
de manera que para los rectángulos I se tiene que B es de contenido cero $\therefore$
$$\sum_{i=1}^{m}\sum_{j=1}^{n}v(R_{ij})<\epsilon$$ Mientras que para
los rectángulos II se tiene que f es continua y por tanto
$$\sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}-m_{ij}A(R_{ij})<\sum_{i=1}^{m}\sum_{j=1}^{n}\frac{\epsilon}{2A(R)}A(R_{ij})$$
$\therefore$ Dada la partición P de R se tiene que
$$\overline{S}(f,P)-\underline{S}(f,P)=\sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}-m_{ij}A(R_{ij})+\sum_{i=1}^{m}\sum_{j=1}^{n}v(R_{ij})<\sum_{i=1}^{m}\sum_{j=1}^{n}\frac{\epsilon}{2A(R)}A(R_{ij})+\frac{\epsilon}{2}$$
$$=\frac{\epsilon}{2A(R)}A(R_{ij})\sum_{i=1}^{m}\sum_{j=1}^{n}A(R_{ij})+\frac{\epsilon}{2}=\frac{\epsilon}{2A(R)}A(R)+\frac{\epsilon}{2}=\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon~\blacksquare$$

$\textcolor{Blue}{Teorema}$: Sea f una función definida en un rectángulo R. Si el conjunto S de puntos donde f es discontinua tiene contenido cero, entonces f es integrable sobre R.

$\textcolor{Blue}{Demostración}$: Sea $\epsilon>0$ dado y sea $\textcolor{Red}{R_{1},R_{2},…,R_{k}}$ el conjunto de rectángulos que cubren a S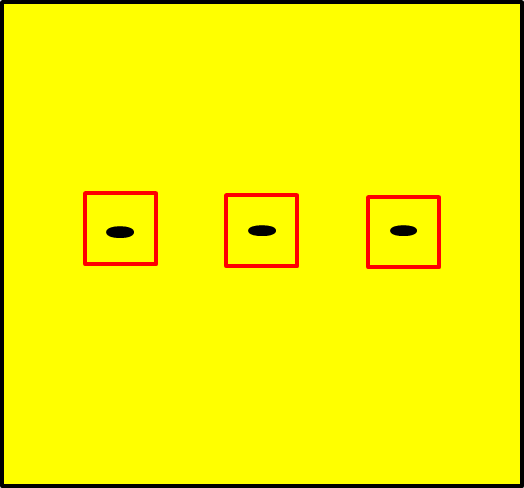

tal que
$$\sum_{i=1}^{k}A(R_{i})<\epsilon$$
si se colocan sobre cada $\textcolor{Red}{R_{j}}$ un rectángulo $\textcolor{Green}{R’_{j}}$ con el mismo centro pero del doble de dimensiones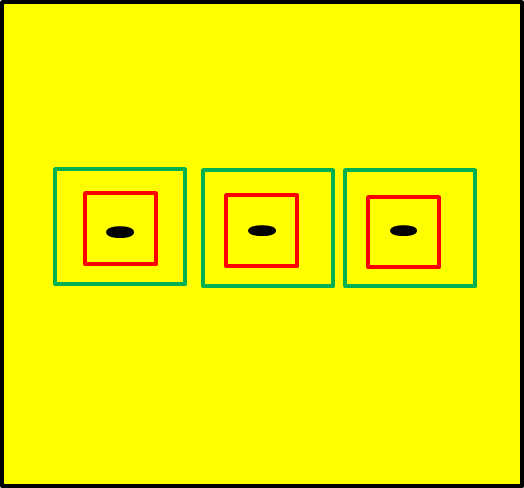

se tiene que
$$\sum_{i=1}^{k}A(\textcolor{Green}{R’{i}})=\sum{i=1}^{k}4A(\textcolor{Red}{R_{i}})<4\epsilon$$
Además, entre los rectángulos $\textcolor{Red}{R_{j}}$ habrá un lado más corto. Denotemos su longitud por $2r$

si tomo el conjunto $R’$ el resto de R después que se han eliminado los interiores de los $\textcolor{Red}{R_{j}}$.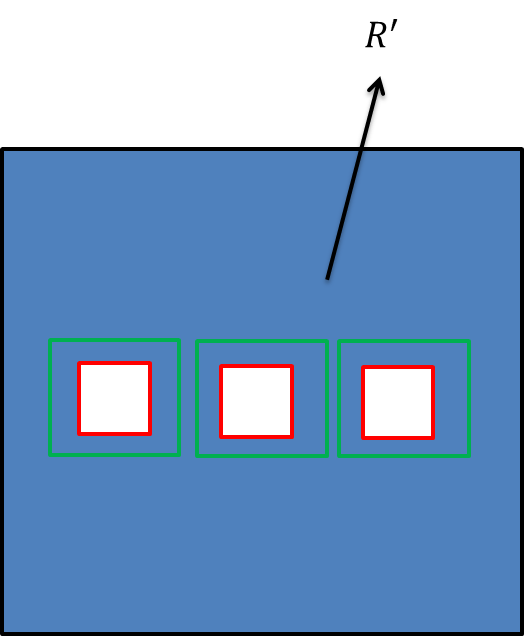

Se tiene que sobre $R’$ f es continua y por tanto uniformemente continua por lo tanto
$$|f(p)-f(q)|<\epsilon~si~|p-q|<\delta$$para cualesquiera p,q en $R’$\Sea $P$ una partición de R tal que $|P|<\delta<r$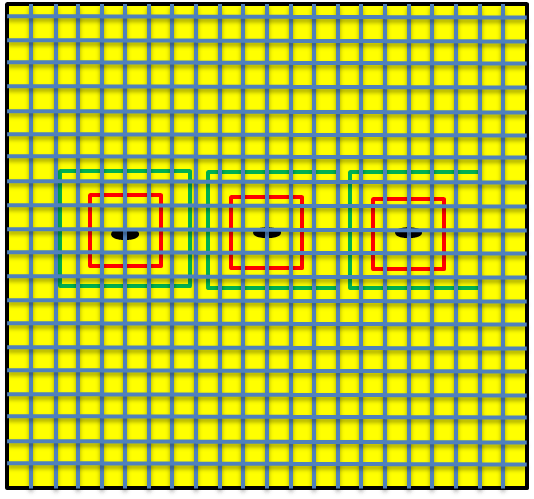

Vamos a estimar
$$\overline{S}(f,P)-\underline{S}(f,P)$$
Para esto dividimos los rectángulos de la partición P en dos conjuntos
$$\textcolor{Green}{R'{j}}\bigcap \textcolor{Red}{R{j}}\neq\emptyset~~~~\textcolor{Green}{R'{j}}\bigcap \textcolor{Red}{R{j}}=\emptyset$$
se tiene entonces que
$$\overline{S}(f,P)-\underline{S}(f,P)=\sum_{i=1}^{n}\sum_{j=1}^{m}(M_{ij}-m_{ij})A(R_{ij})=$$
$$\left(\sum\sum(M_{ij}-m_{ij})A(R_{ij})\right){\textcolor{Green}{R'{j}}\bigcap \textcolor{Red}{R_{j}}\neq\emptyset}+\left(\sum\sum(M_{ij}-m_{ij})A(R_{ij})\right){\textcolor{Green}{R'{j}}\bigcap \textcolor{Red}{R_{j}}=\emptyset}<4M\epsilon+\epsilon A=\epsilon(4M+A)$$
donde $M=\sup{f(x)}$ sobre R.$~\blacksquare$