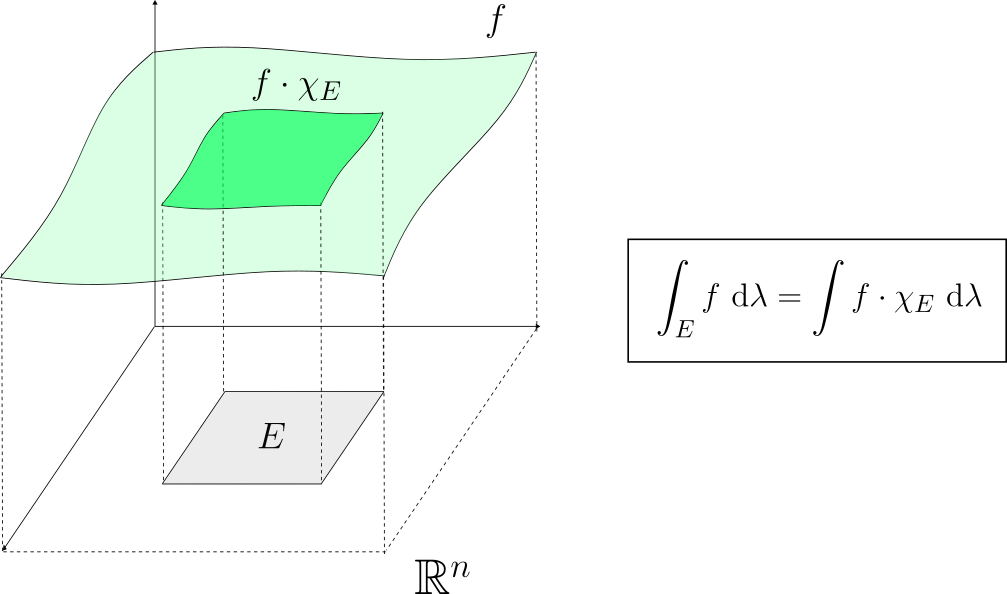
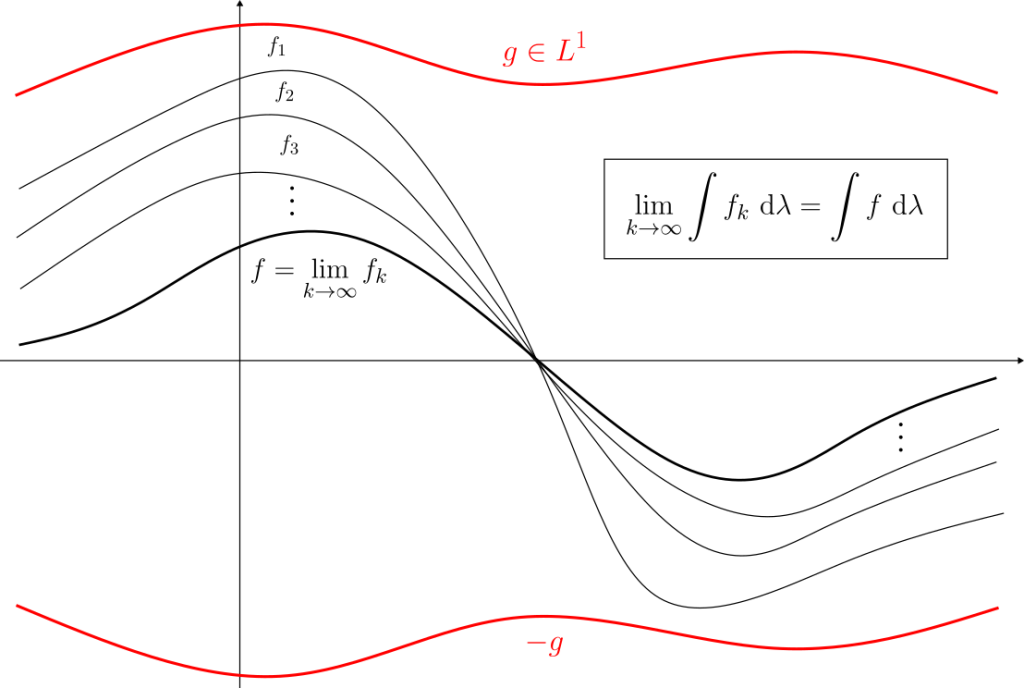
Introducción

En las entradas pasadas desarrollamos una gran cantidad de resultados asociados a la integral de Lebesgue que demuestran que ésta tiene propiedades analíticas muy interesantes. Sin embargo, quedan dos preguntas importantes por responder: ¿Cuál es la relación que existe entre la noción «clásica» de integración (i.e. la integral de Riemann) y la integral de Lebesgue? ¿Cómo podemos evaluar integrales de funciones «sencillas»? (por ejemplo polinomios, funciones trigonométricas y exponenciales).

En esta entrada responderemos esa pregunta. Veremos que una función Riemann integrable es automáticamente $L^1$ y que las dos nociones de integral coinciden. Esto tiene una consecuencia importante: Si la función es Riemann integrable, podemos reducir el cálculo de la integral de Lebesgue a una integral de Riemann y usar todas las herramientas que ya conocemos de estas para calcular integrales (por ejemplo el teorema fundamental del cálculo, cambios de variable, etc.).

Breve repaso de la integral de Riemann

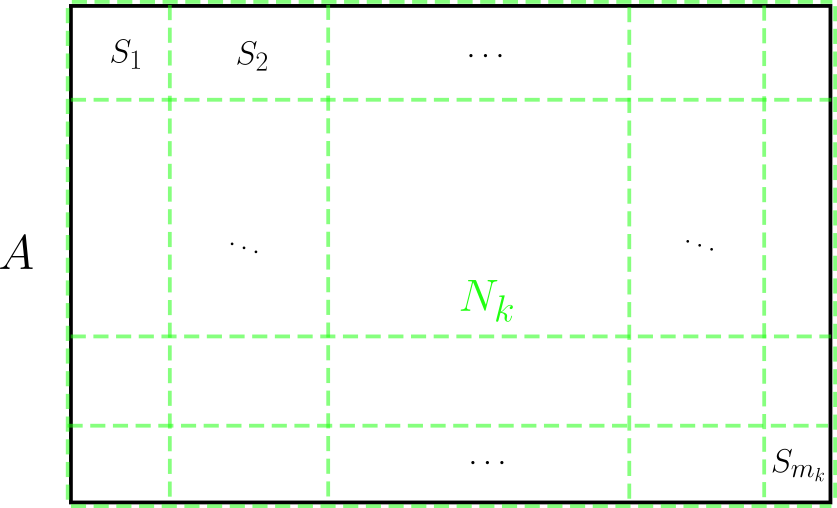
Una partición $P$ de un intervalo cerrado $[a,b]$ es una secuencia de puntos $a=t_0<t_1<\dots< t_k=b$. Una partición de un rectángulo cerrado $A=[a_1,b_1]\times\dots\times [a_n,b_n]$ es una colección $P=(P_1,\dots,P_n)$ donde cada $P_i$ es una partición del intervalo $[a_i,b_i]$. Si $P_i$ divide a $[a_i,b_i]$ en $l_i$ intervalos consecutivos, entonces $P=(P_1,\dots,P_n)$ divide a $A$ en $l_1\cdot l_2\cdot \dots \cdot l_n$ subrectángulos (formados por productos de subintervalos inducidos por la partición). Denotaremos a la colección de dichos subrectángulos como $R_P$.

Definimos el diámetro de una partición $P=(P_1,\dots,P_n)$ como el supremo de los diámetros de los rectángulos inducidos: $$diam(P)=\sup_{S\in R_P} \{ diam(S) \}. $$

Sea $f:A\to \mathbb{R}$ una función acotada sobre un rectángulo $A$ y $P$ una partición de $A$. Para cada subrectángulo $S\in \mathcal{R}_P$ definimos

\begin{align*}
m_S &= \inf \{ f(x) \ | \ x\in S \} \\
M_S &= \sup \{f(x) \ | \ x\in S \}.
\end{align*}

Definimos las sumas inferiores y superiores de $f$ asociadas a la partición $P$ como:
$$L(f,P)=\sum_{S\in R_P}m_s|S|; \ \ \ U(f,P)=\sum_{S\in R_P}M_s|S|.$$
Donde $|S|=\lambda(S)$ es el volúmen (o equivalentemente medida) del rectángulo $S$.

Decimos que una partición $P’=(P_1′,\dots, P_n’)$ refina a $P=(P_1,\dots, P_n)$ si $P_k\subseteq P_k’$ para cada $k=1,2,\dots,n$. (Esto es, cada subrectángulo de $P’$ está contenido en un subrectángulo de $P$).

El siguiente Lema es estándar. Omitimos la demostración, ésta puede ser consultada en la mayoría de textos.

Lema. Si $P’$ refina a $P$, entonces $$L(f,P)\leq L(f,P’)\leq U(f,P’)\leq U(f,P).$$

Decimos que una función acotada $f:A\to \mathbb{R}$ es Riemann integrable si $$\sup_P \{ L(f,P) \}=\inf_P\{ U(f,P) \}.$$

El valor común $\sup_P \{ L(f,P) \}=\inf_P\{ U(f,P) \}$ es llamado la integral de Riemann de $f$ sobre $A$ y lo denotaremos provisionalmente como $$ \int_{\mathcal{R},A} f(x) \ \mathrm{d}x.$$

Una clase importante de funciones Riemann integrables son las funciones continuas:

Proposición. Si $f$ es una función continua sobre un rectángulo $A$ entonces $f$ es Riemann integrable.

Omitimos la demostración.

Las integrales de Riemann y Lebesgue

Teorema. Sea $f$ una función acotada sobre un rectángulo $A$.

1. Si $f$ es Riemann integrable, entonces $f\in L^1(A)$. Además $$\int_{\mathcal{R},A} f(x) \ \mathrm{d}x=\int_A f \ \mathrm{d}\lambda .$$
2. $f$ es Riemann integrable sobre $A$ si y sólo si $D=\{ x\ | \ f \ \text{es discontinua en } x\} $ tiene medida de Lebesgue cero.

Demostración. Supongamos que $f$ es Riemann integrable. Para cada partición $P$ definamos:

$$g_P=\sum_{S\in R_P}m_S \chi_{S}; \ \ \ G_P=\sum_{S\in R_P}M_S \chi_{S}.$$

Si bien los rectángulos $S\in R_P$ no son ajenos, sólo se intersectan en conjuntos de medida cero (sus fronteras). Usando que $\lambda(S)=|S|$, concluimos facilmente:

\begin{equation} \int_A g_P \ \mathrm{d}\lambda=L(f,P); \ \ \ \int_A G_P \ \mathrm{d}\lambda= U(f,P). \end{equation}

Como $\sup_P \{ L(f,P) \}=\inf_P\{ U(f,P) \}=\int_{\mathcal{R},A} f(x) \ \mathrm{d}x$, podemos encontrar una sucesión de particiones $P_1,P_2,\dots$ tales que $L(f,P_k),U(f,P_k)\longrightarrow \int_{\mathcal{R},A} f(x) \ \mathrm{d}x$ cuando $k\longrightarrow \infty$. Por el Lema podemos suponer sin pérdida de generalidad que para cada $k=1,2,\dots$, $P_{k+1}$ refina a $P_k$ y el diámetro de $P_k$ es menor a $\frac{1}{k}$.

Consideremos $$N_k=\bigcup_{S\in R_{P_k}}\partial S, $$ (Donde $\partial A$ denota la frontera del conjunto $A$ ).

Definamos $$N=\bigcup_{k\in \mathbb{N}}N_k.$$ Es decir, $N$ es el conjunto de puntos que está en la frontera de alguno de los rectángulos inducidos por $P_k$ para algún $k$. Cada $N_k$ es un conjunto nulo (pues está contenido en una cantidad finita de hiperplanos) $\implies$ $N$ es un conjunto nulo. $(2)$

Observemos que cualquier punto $x\notin N$ está estrictamente en el interior de cada rectángulo $S\in R_{P_k}$ al que pertenece. Esto nos garantiza que $g_{P_1}(x)\leq g_{P_2}(x)\leq \dots f$ y $G_{P_1}(x)\geq G_{P_2}(x)\geq \dots f$. Pues si $x\in T\subseteq S$ con $S\in R_{P_k}; T\in R_{P_{k+1}}$, entonces $g_{P_k}(x)=m_S\leq m_T=g_{P_{k+1}}(x)\leq f(x)$ y $G_{P_k}(x)=M_S\geq M_T=G_{P_{k+1}}(x)\geq f(x)$. Además $|g_{P_k}(x)|,|G_{P_k}(x)|\leq \sup_{ A} |f|$. $(3)$

Por lo anterior, deducimos que $g_{P_k}$ es una sucesión crecieciente y acotada en c.t.p. mientras que $G_{P_k}$ es una sucesión decreciente y acotada en c.t.p. Esto garantiza que $g_{P_k}$ y $G_{P_k}$ convergen a ciertas funciones $g$ y $G$ con $g\leq f \leq G$ en c.t.p. Además, ambas sucesiones están acotadas en norma por $\sup_{A} |f|$. Se sigue del teorema de la convergencia dominada y (1) que:

$$\int_{\mathcal{R},A} f(x) \ \mathrm{d}x=\lim_{k\to \infty}L(f,P_k)=\lim_{k\to \infty} \int_A g_{P_k} \ \mathrm{d}\lambda=\int_A g \ \mathrm{d}\lambda.$$ $$\int_{\mathcal{R},A} f(x) \ \mathrm{d}x=\lim_{k\to \infty}U(f,P_k)=\lim_{k\to \infty} \int_A G_{P_k} \ \mathrm{d}\lambda=\int_A G \ \mathrm{d}\lambda.$$

Como $G-g\geq 0$ (en c.t.p.) y $\int (G-g) \ \mathrm{d}\lambda=0$, se sigue que $G=g$ en c.t.p. $\implies$ $G=f=g$ en c.t.p. $\implies$ $f$ es medible. Más aún, $f\in L^1(A)$ pues es una función medible y acotada (en c.t.p.) de $A$. Por monotonía la única posibilidad es:

\begin{equation*}
\int f \ \mathrm{d}\lambda=\int g \ \mathrm{d}\lambda=\int G \ \mathrm{d}\lambda=\int_{\mathcal{R},A} f(x) \ \mathrm{d}x.
\end{equation*}

Se sigue 1.

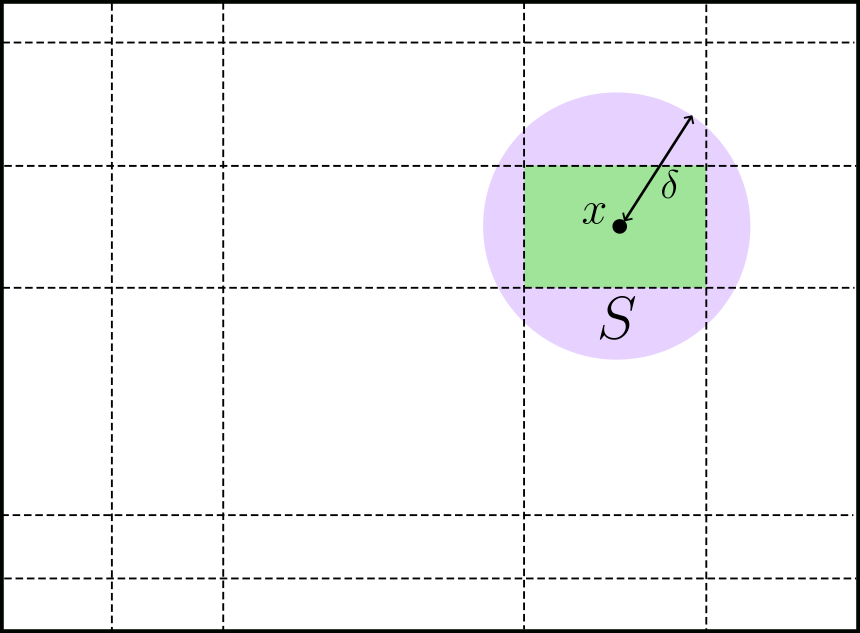
Veamos la dirección ($\implies$) en 2. Supongamos que $f$ es Riemann integrable. Consideremos las funciones: $$h(x)=\lim_{\delta\to 0} \inf_{|y-x|\leq \delta}f(y); \ \ \ H(x)=\lim_{\delta\to 0} \sup_{|y-x|\leq \delta}f(y).$$

$h$ y $H$ están bien definidas pues $f$ es acotada. Desentrañando las definiciones es fácil ver que $H(x)=h(x)$ si y sólo si $f$ es continua en $x$.

Usando la notación del inciso anterior, definamos $N’=N\cup \{ x \ | \ g(x)\neq G(x) \}$. Anteriormente probamos que los dos uniendos son nulos, de modo que $N’$ es nulo.

Probaremos que si $x\notin N’$ $\implies$ $H(x)=h(x)$. Esto en particular prueba que $f$ es continua en c.t.p. Sea entonces $x\in A\setminus N’$.

Sea $\varepsilon>0$. Como $\lim_{k\to \infty} g_k(x)=g(x)=G(x)=\lim_{k\to \infty} G_k(x)$, podemos encontrar una $M\in \mathbb{N}$ suficientemente grande tal que $$G_M(x)-g_M(x)<\frac{\varepsilon}{2}.$$

Sea $S$ el rectángulo inducido por $P_M$ tal que $x\in S$. Como observamos anteriormente, $x$ está en el interior de $S$, de modo que podemos encontrar $\eta>0$ suficientemente pequeño tal que $$\{y \ | \ |x-y|<\eta \}\subseteq S.$$ Luego, $\forall \delta$ con $0<\delta\leq \eta$:
$$G_M(x)= \sup_{y\in S} f(y)\geq \sup_{|y-x|\leq \delta} f(y)\geq \inf_{|y-x|\leq \delta}f(y) \geq \inf_{y\in S} f(y) = g_M(x)$$ $$\implies \sup_{|y-x|\leq \delta} f(y)- \inf_{|y-x|\leq \delta}f(y)\leq G_M(x)-g_M(x)<\varepsilon.$$ Como esto se satisface para cualquier $\varepsilon>0$, necesariamente $$h(x)=\lim_{\delta\to 0} \inf_{|y-x|\leq \delta}f(y)=\lim_{\delta\to 0} \sup_{|y-x|\leq \delta}f(y)=H(x).$$ Esto prueba la implicación ($\implies$) de 2.

La implicación ($\impliedby$) es esencialmente revertir los pasos anteriores: Tomemos una sucesión de particiones $P_1\subseteq P_2\subseteq\dots$ cuyo diámetro se haga arbitrariamente pequeño y definamos $g_k,G_k,g,G,N,h,H$ como antes (notemos que las observaciones (2) y (3) siguen siendo ciertas). En este caso como $f$ es continua en c.t.p. $\implies$ $h=H$ en c.t.p.

Afirmamos que si $H(x)=h(x)$ con $x\notin N$ $\implies$ $g(x)=G(x)$: $\ \ \ (4)$

Dado $\varepsilon>0$, por la definición de $h,H$, podemos encontrar $\delta>0$ suficientemente pequeño tal que $\sup_{|y-x|\leq \delta} f(y)-\inf_{|y-x|\leq \delta} f(y)<\varepsilon$. Como el diámetro de las particiones se vuelve arbitrariamente pequeño, podemos encontrar $P_N$ con $N$ suficientemente grande tal que $x\in S \in R_{P_N}$ y $S\subseteq \{ y \ | \ |y-x|\leq \delta \}$.

Como $x\notin N$, sabemos que $g_{P_N}(x)=m_S$, $G_{P_N}(x)=M_S$. Luego, para $k\geq N$: \begin{align*}
G_{P_k}(x)-g_{P_k}(x) &\leq G_{P_N}(x)-g_{P_N}(x) \\
&= M_S-m_S \\
&= \sup_{S} f-\inf_{S} f\\
&\leq \sup_{|y-x|\leq \delta} f(y)-\inf_{|y-x|\leq \delta} f(y) \\
&< \varepsilon.
\end{align*} Como $x\notin N$, tenemos que $g_{P_k}(x)\uparrow g(x)$; $G_{P_k}(x)\downarrow G(x)$ (ver (3) ). Esto y la desigualdad anterior implican que $g(x)=G(x)$.

Como $h=H$ en c.t.p. y $N$ es nulo, se sigue de (4) que $g=G$ en c.t.p.

Finalmente, aplicando el teorema de la convergencia dominada y (1): \begin{align*}
\lim_{k\to \infty}L(f,P_k) &= \lim_{k\to \infty} \int_A g_{P_k} \ \mathrm{d}\lambda \\
&= \int_A g \ \mathrm{d}\lambda \\
&= \int_A G \ \mathrm{d}\lambda \\
&= \lim_{k\to \infty} \int_A G_{P_k} \ \mathrm{d}\lambda \\
&= \lim_{k\to \infty}U(f,P_k)
\end{align*}(Podemos aplicar el teorema de la convergencia dominada pues todas las funciones en cuestión están dominadas por $\sup |f|$).

Por lo anterior, concluimos que $f$ es Riemann integrable.

$\square$

Cálculo de integrales

El teorema de la sección anterior nos permite reducir el cálculo de integrales de Lebesgue al cálculo de integrales de Riemann mientras las funciones sean Riemann integrables. Esto puede simplificar en gran medida los cálculos pues nos posibilita usar las herramientas conocidas para la integral de Riemann, como el teorema fundamental del cálculo, la integración por partes, los cambios de variable, entre otros.

Esto se aprecia mejor con un ejemplo.

Ejercicio. Calcular la integral de Lebesgue $$\int_0^{\infty} e^{-x} \ \mathrm{d}x.$$

Solución. La sucesión $g_N(x)=e^{-x}\chi_{[0,N]}$ es una sucesión creciente de funciones medibles positivas. Claramente $\lim_{N\to \infty} g_N(x)=e^{-x}\chi_{[0,\infty)}$. Luego, por el teorema de la convergencia monótona:

$$\int_0^{\infty}e^{-x} \ \mathrm{d}x=\lim_{N\to \infty}\int_{\mathbb{R}}g_N(x) \ \mathrm{d}x=\lim_{N\to \infty}\int_0^Ne^{-x} \ \mathrm{d}x.$$

Al ser continuas, las funciones del lado derecho son Riemann integrables sobre $[0,N]$. Por el teorema anterior, el cálculo de estas integrales (de Lebesgue) se reduce al cálculo de las integrales de Riemann, por lo que podemos usar el teorema fundamental del cálculo:

\begin{align*}
\int_0^{\infty}e^{-x} \ \mathrm{d}x &= \lim_{N\to \infty}\int_0^Ne^{-x} \ \mathrm{d}x \\ &= \lim_{N\to \infty}\int_0^N (-e^{-x})’ \ \mathrm{d}x \\ &= \lim_{N\to \infty} \left[-e^{-x} \right]_{x=0}^{x=N} \\ &= \lim_{N\to \infty} [-e^{-N}+e^0] \\ &=1-\lim_{N\to \infty} e^{-N} \\ &=1.
\end{align*}

$\triangle$

Observación. El argumento usado en el ejercicio anterior para calcular integrales sobre intervalos no acotados mediante T.F.C. es bastante común: Por ejemplo si $g’\geq 0$ (ó $g’\in L^1(\mathbb{R})$), entonces por el Teorema de la convergencia monótona (o dominada) tenemos $$\int_{-\infty}^{\infty} g'(x) \ \mathrm{d}x=\lim_{N\to \infty} \int_{-N}^{N}g'(x) \ \mathrm{d}x=\lim_{N\to \infty} [g(N)-g(-N)]=\lim_{x\to \infty}g(x)-\lim_{x\to -\infty}g(x).$$

Por brevedad, abreviaremos el argumento anterior diciendo simplemente que $$\int_{-\infty}^{\infty} g'(x) \ \mathrm{d}x= [g(x)]_{x=-\infty}^{x=\infty}=g(\infty)-g(-\infty). $$

Haremos consideraciones similares para los demás tipos de intervalos no acotados.

$\square$

El criterio del teorema anterior nos da otro argumento para ver que la función de Dirichlet no es Riemann integrable.

Ejemplo. La función de Dirichlet $\chi_{\mathbb{Q}}$ no es Riemann integrable en $[0,1]$, pues no es continua en ningún punto de este intervalo.

Ejercicio. Probar que la función $f(x)=\frac{x}{(x^2+x+1)\ln(1+x)^2}\in L^1([1,\infty))$.

Solución. Observemos primero que $f\geq 0$ en $[1,\infty)$. En vez de calcular directamente $\int_1^{\infty}f(x) \ \mathrm{d}x$, es suficiente encontrar alguna función $g\in L^1([1,\infty))$ tal que $0\leq f\leq g$. Consideremos entonces $$g(x)=\frac{1}{(x+1)(\ln (x+1))^2}.$$ Como $x+1\leq \frac{x^2+x+1}{x}$ para $x\in [0,\infty)$ $\implies$ $f\leq g$ en $[0,\infty)$. Por el teorema fundamental del cálculo:

\begin{align*}
\int_1^{\infty} g(x) \ \mathrm{d}x &= \int_1^{\infty} \frac{1}{(x+1)(\ln (x+1))^2} \ \mathrm{d}x \\
&= \int_1^{\infty} \left( -\frac{1}{\ln(x+1)} \right)’ \ \mathrm{d}x \\
&= \left[ -\frac{1}{\ln(x+1)} \right]_{x=1}^{x=\infty} \\ &= \frac{1}{\ln(2)} -\lim_{x\to \infty} \frac{1}{\ln(x+1)} \\
&= \frac{1}{\ln(2)}-0\\
&= \frac{1}{\ln(2)}<\infty.\\
\end{align*}

(En las igualdades anteriores abreviamos la aplicación del teorema de la convergencia monótona como en la observación). Finalmente $$\int_1^{\infty} f(x) \ \mathrm{d}x=\int_1^{\infty} g(x) \ \mathrm{d}x=\frac{1}{\ln(2)}<\infty.$$

$\triangle$

Más adelante…

Veremos el teorema de cambio de variable para integrales de Lebesgue. Análoga al de las integrales de Riemann, nos permite «cambiar coordenadas» en las integrales para reescribirlas de manera conveniente.

Tarea moral

• Calcula $$\int_{-\infty}^{\infty}\frac{1}{1+x^2} \ \mathrm{d}x.$$
• Calcula $$\int_{0}^{1} \frac{1}{\sqrt{x}} \ \mathrm{d}x.$$
• Sea $f(x)=x^{\alpha}$.
  • Demuestra que $f\in L^1((0,1))$ $\iff$ $\alpha<1$.
  • Demuestra que $f\in L^1([1,\infty))$ $\iff$ $\alpha>1$.
• ¿Si una función es continua en casi todo punto de $\mathbb{R}$, podemos asegurar que $f$ es continua en todo $\mathbb{R}$?
• Sea $f:[a,b]\to \mathbb{R}$ una función monótona. Demuestra que $f$ es discontinua en a lo más una cantidad numerable de puntos. Deduce que $f$ es Riemann integrable. [SUGERENCIA: Si $f$ es discontinua en $x_0$, la única posibilidad es que $s(x_0)=\inf_{x>x_0}\{ f(x)\}-\sup_{x<x_0}\{ f(x) \}>0$. Si hay una cantidad no numerable de discontinuidades, entonces existe algún $N\in \mathbb{N}$ tal que $\{y \ | \ s(y)>\frac{1}{N} \}$ es infinito. ¿Porqué esto es imposible? ].

Introducción

En las secciones pasadas probamos muchas propiedades interesantes de los conjuntos medibles y la medida de Lebesgue. Una omisión importante es ¿Qué pasa con las transformaciones rígidas? O más generalmente ¿Cómo interactua la medida de Lebesgue con las transformaciones lineales?
En dimensiones bajas estamos acostumbrados a que la longitud, el área y el volúmen sean invariantes bajo transformaciones rígidas; o que se multipliquen por «cierto factor» bajo transformaciones lineales generales. Así que es de esperar que algo similar ocurra con la medida de Lebesgue.
En esta entrada discutiremos de manera precisa cuál es la relación entre $\lambda(A)$ y $\lambda (TA)$ cuando $T$ es una matriz arbitraria.

Nuestro objetivo es probar lo siguiente:

Teorema. Sea $T\in M_{n\times n}(\mathbb{R})$ una matriz y $A\subseteq\mathbb{R}^n$. Entonces $$\lambda^*(TA)=|\det T|\lambda^*(A).$$ Si $A$ es medible entonces $TA$ es medible y $$\lambda(TA)=|\det T|\lambda(A).$$

Demostración.

Veremos primero el caso en el que $T$ es invertible.

Podemos hacer una serie de reducciones para simplificar la demostración. Considera lo siguiente.

Observación 1. Si el teorema es válido para dos matrices $T_1$ y $T_2$, entonces es válido para el producto $T_1T_2$ pues $$|\det T_1T_2|=|\det T_1||\det T_2|.$$ De donde $$\lambda^*(T_1T_2A)=|\det T_1|\lambda^*(T_2A)=|\det T_1||\det T_2|\lambda^*(A)=|\det T_1T_2|\lambda^*(A).$$ Y si $A$ es medible $\implies$ $T_2A$ es medible $\implies$ $T_1T_2A$ es medible.

Hecho 1. De tus cursos anteriores seguramente recordarás que toda matriz invertible se puede descomponer como producto de las llamadas «matrices elementales». Puedes consultarlo aquí [ENLACE]. Como un breve recordatorio, existen dos tipos de matrices elementales. En lo que sigue $k$ y $l$ denotan enteros fijos entre $1$ y $n$.

Matrices de multiplicación. Dado $c\in \mathbb{R}$, son matrices de la forma $M=[m_{ij}]$ con:

\begin{equation*} m_{ij}= \begin{cases} 1 & \text{si } i= j\neq k \\ c & \text{si } i= j= k \\ 0 & \text{si } i\neq j \end{cases} \end{equation*}

Por ejemplo cuando $k=1$:

\begin{equation*} \begin{pmatrix} c & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \end{equation*}

Observa que $|\det M|=c$, además que $ M^{-1}$ es también una matriz de multiplicación con $c$ reemplazado por $c^{-1}$. Dada una matriz $T$, $MT$ es la matriz que se obtiene de $T$ al multiplicar su $k$-ésima fila por $c$. Algo similar ocurre con $TM$ reemplazando «filas» por «columnas». Como transformación lineal, $M$ actúa multiplicando la $k$-ésima componente de un vector por $c$.

Matrices de suma. Dado $c\in \mathbb{R}$, son matrices $A=[a_{ij}]$ de la forma:

\begin{equation*} a_{ij}= \begin{cases} 1 & \text{si } i= j\neq k \\ c & \text{si } i=k, j=l \\ 0 & \text{si } i\neq j \end{cases} \end{equation*}

Por ejemplo, cuando $k=1,l=2$:

\begin{equation*} \begin{pmatrix} 1 & c & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \end{equation*}

Observa que $|\det A|=1$ y que $ A^{-1}$ es también una matriz de multiplicación con $c$ reemplazado por $-c$. Dada una matriz $T$, $AT$ es la matriz que se obtiene de $T$ al sumar $c$ veces la fila $l$ a la fila $k$. Algo similar ocurre con $TA$ reemplazando «filas» por «columnas». Como transformación lineal ésta actúa sobre un vector sumando $c$ veces la $l$-ésima entrada a su $k$-ésima entrada.

Por las observaciones anteriores, resulta que es suficiente probar el teorema para las matrices elementales, que denotaremos por $E_{n\times n}$.

Veamos ahora el siguiente Lema.

Lema. Sea $T\in M_{n\times n}(\mathbb{R})$ una matriz invertible. Sea $J$ el rectángulo semiabierto:
$$J=[0,1)\times \dots \times[0,1).$$
Sea $\rho$ el cociente: $$\rho=\frac{\lambda(TJ)}{\lambda(J)}.$$
Dado $A\subseteq \mathbb{R}^n$, entonces $$\lambda^*(TA)=\rho\lambda^*(A).$$ Si $A$ es medible, entonces $TA$ es medible y $$\lambda(TA)=\rho\lambda(A).$$

Demostración. La transformación lineal $x\to Tx$ es continua con inversa continua, por tanto un homeomorfismo. En particular transforma conjuntos abiertos en conjuntos abiertos y conjuntos compactos en conjuntos compactos.

Podemos expresar a $J$ como unión creciente de rectángulos, a saber: $$J=\bigcup_{k=1}^{\infty} [0,1-k^{-1}]\times[0,1-k^{-1}]\times \dots \times [0,1-k^{-1}].$$ Por la monotonía de la medida de Lebesgue es fácil ver que $\lambda(J)=1>0$. Aplicando $T$ (y usando que en general $f(\bigcup_{i\in I }C_i)=\bigcup_{i\in I} f(C_i)$) se sigue que: $$TJ=\bigcup_{k=1}^{\infty} T([0,1-k^{-1}]\times[0,1-k^{-1}]\times \dots \times [0,1-k^{-1}]).$$ Como $T$ es un homeomorfismo, cada $T([0,1-k^{-1}]\times[0,1-k^{-1}]\times \dots \times [0,1-k^{-1}])$ es un conjunto compacto. Entonces $TJ$ es unión numerable de conjuntos compactos por lo que en particular es medible.

Como $J$ es acotado, $TJ$ también es acotado así que su medida es finita. En todo caso, el cociente $\rho$ tiene sentido y está bien definido.

Veamos primero que el Lema se satisface para conjuntos abiertos. Considera $G$ un conjunto abierto arbitrario.

La idea es cubrir a $G$ con una cantidad numerable de «copias reescaladas» y ajenas de $J$. El procediemiento es estándar:

Primero cubrimos $\mathbb{R}^n$ con rectángulos de la forma $$[\alpha_1,\alpha_1+1)\times [\alpha_2,\alpha_2+1)\times \dots \times [\alpha_n,\alpha_n+1).$$ Donde cada $\alpha_k\in \mathbb{Z}$ es un número entero. Seleccionamos los rectángulos que están contenidos en $G$. Luego, partimos cada rectángulo no seleccionado en los $2^n$ subrectángulos que se obtienen al bisecar sus lados. Estos son de la forma $$\left[\frac{\alpha_1}{2},\frac{\alpha_1+1}{2}\right)\times \left[\frac{\alpha_2}{2},\frac{\alpha_2+1}{2}\right)\times \dots \times \left[\frac{\alpha_n}{2},\frac{\alpha_n+1}{2}\right).$$ Con $\alpha_k \in \mathbb{Z}$ enteros. De nuevo seleccionamos los rectángulos que están contenidos en $G$. Continuando con este proceso, al final nos quedamos con una colección numerable de copias reescaladas ajenas de $J$: $J_1,J_2,\dots$.

Como $G$ es abierto, para cualquier punto $x\in G$, podemos encontrar un rectángulo $R=[\frac{\alpha_1}{2^m},\frac{\alpha_1+1}{2^m})\times \dots \times [\frac{\alpha_n}{2^m},\frac{\alpha_n+1}{2^m})$ con $\alpha_1, \dots, \alpha_n \in \mathbb{Z}$ tal que $x\in R \subseteq G$. Esto garantiza que cualquier $x\in G$ es eventualmente cubierto por algún $J_k$. Además, claramente cada rectángulo $J_k$ se queda contenido en $G$. Esto nos garantiza que $$G=\bigcup_{k=1}^{\infty} J_k.$$ Es la descomposición deseada. Al aplicar $T$, se sigue también que $$TG=\bigcup_{k=1}^{\infty} TJ_k$$ Es la únión ajena de las imágenes $TJ_k$ (que son medibles).

Cada $J_k$ es una copia reescalada y trasladada de $J$, es decir, es de la forma: $$J_k=z_k+t_kJ$$ Con $z_k\in \mathbb{R}^n$, $t_k>0$. Así que podemos calcular su medida de Lebesgue: $$\lambda(J_k)=t_k^n\lambda(J)$$ $$\implies t_k^n=\frac{\lambda(J_k)}{\lambda(J)}.$$

Ahora, por linealidad se verifica fácilmente que: $$TJ_k=Tz_k+t_kTJ$$ $$\implies \lambda(TJ_k)=t_k^n\lambda(TJ).$$ Sustituyendo $t_k^n$: $$\implies \lambda(TJ_k)=\left( \frac{\lambda(J_k)}{\lambda(J)} \right)\lambda(TJ)=\rho\lambda(J_k).$$

Finalmente, por la aditividad contable:

\begin{align*}
\lambda(TG) =& \lambda\left(\bigcup_{k=1}^{\infty} TJ_k\right) \\
&= \sum_{k=1}^{\infty} \lambda (TJ_k) \\
&= \rho \sum_{k=1}^{\infty} \lambda (J_k) \\
&= \rho \lambda\left( \bigcup_{k=1}^{\infty} J_k \right) \\
&= \rho \lambda(G).
\end{align*}

Esto establece el Lema para el caso de conjuntos abiertos. Si $A\subseteq \mathbb{R}^n$ es un subconunto arbitrario, por la aproximación con abiertos de la medida exterior tenemos:

\begin{align*}
\lambda^*(TA) &= \inf_{TA\subseteq U \text{ abto.}}\{ \lambda(U) \}\\
&= \inf_{A\subseteq U \text{ abto.}}\{ \lambda(TU) \} \\
&= \inf_{A\subseteq U \text{ abto.}}\{ \rho \lambda(U) \} \\
&= \rho \inf_{A\subseteq U \text{ abto.}}\{ \lambda(U) \} \\
&= \rho \lambda^*(A).
\end{align*}

En la segunda igualdad usamos que $T$ es un homeomorfismo.

Finalmente, si $A$ es medible, para cualquier $\varepsilon>0$ podemos encontrar un abierto $U$ tal que $A\subseteq U$ y $$\lambda^*(U\setminus A)<\frac{\varepsilon}{\rho}$$ Entonces $TU$ es un abierto con

$$\lambda^*(TU\setminus TA)=\lambda^*(T(U\setminus A))=\rho \lambda^*(U\setminus A)<\varepsilon.$$
Se sigue que $TA$ es medible y $\lambda(TA)=\lambda^*(TA)=\rho \lambda^*(A)=\rho \lambda(A)$.

$\square$

El Lema anterior nos dice en particular que cuando $T$ es una matriz elemental, existe alguna constante $\rho$ tal que $$\lambda^*(TA)=\rho \lambda^*(A).$$ para cualquier $A\subseteq \mathbb{R}^n$. Queremos probar que $\rho=|\det T|$, para ello es suficiente exhibir algún conjunto particular $A$ (medible, de medida finita y no nula) para el cual podamos calcular $\rho=\frac{\lambda(TA)}{\lambda(A)}$. Tratamos los dos tipos de matrices elementales por separado.

1. $T$ es matriz de multiplicación. Asumamos sin pérdida de generalidad que $T=[t_{ij}]$ con $t_{11}=c$, $t_{ii}=1$ para $i\neq 1$. En este caso $\det T=c$ (los demás casos son análogos). Escojamos $$A=[0,1]\times[0,1]\times \dots \times [0,1] \ \implies \ \lambda(A)=1$$ Si $c>0$ entonces $$TA=[0,c]\times[0,1]\times \dots \times [0,1]\ \implies \ \lambda(TA)=c$$ Y si $c<0$ entonces $$TA=[c,0]\times[0,1]\times \dots \times [0,1]\ \implies \ \lambda(TA)=-c$$ En todo caso
   $$\rho=\frac{\lambda(TA)}{\lambda(A)}=|c|=|\det T|.$$
2. $T$ es matriz de adición. Nuevamente, por simplicidad asumiremos que $T$ es de la forma
   \begin{equation*} T=\begin{pmatrix} 1 & c & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \end{equation*}
   Y que $c>0$. Los demás casos son completamente análogos. Ahora, escojamos $$A=\{x\in \mathbb{R}^n \ : \ -cx_2\leq x_1\leq 0, 0\leq x_2 \leq 1, \dots, 0\leq x_n \leq 1\}.$$ Es fácil ver que $$TA=\{x\in \mathbb{R}^n \ : \ 0\leq x_1\leq cx_2, 0\leq x_2 \leq 1, \dots, 0\leq x_n \leq 1\}.$$ Si $M$ es la matriz de multiplicación
   \begin{equation*} M=\begin{pmatrix} -1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \end{equation*}
   Para este $A$ en particular tenemos que $$TA=MA.$$ Así que por el caso anterior tenemos $$\lambda(TA)=\lambda(MA)=|\det M|\lambda(A)=\lambda(A).$$ De donde $$\rho=\frac{\lambda(TA)}{\lambda(A)}=1=|\det T|.$$

Esto concluye la prueba para matrices elementales y por tanto, para todas las matrices invertibles. Veamos ahora el caso degenerado en el que $\det T=0$. En este caso es suficiente probar que directamente $\lambda(T\mathbb{R}^n)=0$.

Si $\det T =0$, los vectores columna de la matriz $T$ son linealmente dependientes, por lo que generan el subespacio $T\mathbb{R}^n$ de dimensión $m<n$. Por Gram-Schmidt, podemos escojer una base ortonormal $B=\{b_1,b_2,\dots,b_n \}$ de $\mathbb{R}^n$ tal que $\{ b_1,b_2,\dots, b_m \}$ sean base de $S$.

Sea entonces $M$ la matriz cuyos vectores columna son $b_1,b_2,\dots b_n$ en ese órden (ésta es ortogonal, y por tanto $|\det M|=1$). $M$ transforma la base usual de $\mathbb{R}^n$ en la base $B$, i.e. $Me_i=b_i$ (donde $e_i$ es el vector con $i$-ésima entrada 1 y las demás 0). Se sigue que: $$M(\mathbb{R}^m\times\{ 0\}^{n-m})=T\mathbb{R}^n.$$ Entonces, usando el caso no degenerado tenemos:

\begin{align*}
\lambda(T\mathbb{R}^n) &= \lambda(M(\mathbb{R}^m\times\{ 0\}^{n-m})) \\
&= |\det M|\lambda(\mathbb{R}^m\times\{ 0\}^{n-m}) \\
&\leq \lambda(\mathbb{R}^{n-1}\times\{ 0\}) \\
&= 0.
\end{align*}

Pues ya sabemos que el hiperplano $\mathbb{R}^{n-1}\times\{ 0\}$ tiene medida cero.

$\square$

Más adelante…

Definiremos el concepto de sigma-álgebra y funciones medibles, las estructuras abstractas sobre las que podemos definir la integral de Lebesgue y otros conceptos de integración más generales.

Tarea moral

• Sea $T:\mathbb{R}^n\to \mathbb{R}^n$ una transformación lineal y $x\in \mathbb{R}^n$. ¿Que relación existe entre $\lambda^*(A)$ y $\lambda^*(TA+x)$?
• Demuestra que la medida de Lebesgue es invariante bajo rotaciones.
• Calcula la medida de Lebesgue del paralelogramo $P$ con vértices $(0,0),(2,1),(3,4)$ y $(1,3)$. [SUGERENCIA: La transformación con matriz $T= \begin{pmatrix} 2 & 1 \\ 1 & 3 \end{pmatrix}$ transforma el rectángulo $[0,1]\times [0,1]$ en $P$].
• Sean $a_1,a_2,\dots, a_n \in \mathbb{R}^n$. Escribamos $a_j=(a_{1j},a_{2j},\dots, a_{nj})$ para $j=1,\dots, n$. Sea $R$ el paralelepípedo $$R= \{ t_1a_1+t_2a_2+\dots+t_na_n \ | \ 0\leq t_k \leq 1 \ \ \ \forall k \}.$$ Demuestra que $\lambda(R)=|\det A|$, donde $A=[a_{ij}]$.

Introducción

Hasta ahora, hemos estudiado la integral de Lebesgue para funciones definidas (en c.t.p.) de $\mathbb{R}^n$. Sin embargo, quizá como analogía con la integral de Riemann, es esperable que podamos definir la integral sobre conjuntos más generales, por ejemplo rectángulos o esferas. Esto es precisamente lo que estudiaremos en esta sección.

Definición y convenciones

Si queremos integrar una función $f$ sobre un conjunto $E$, una noción bastante natural es la siguiente:

Definición. Dada una función medible $f:\mathbb{R}^n\to [-\infty, \infty]$ y un conjunto medible $E\subseteq \mathbb{R}^n$, definimos la integral de $f$ sobre $E$ (cuando tenga sentido) como: $$\int_E f \ \mathrm{d}\lambda=\int f\cdot \chi_E \ \mathrm{d}\lambda.$$ Donde $\chi_E$ es la función característica de $E$.

Si una función $f$ solamente está definida en casi todo punto de $E$, es decir, $f:E\setminus N \to [-\infty,\infty]$ (con $\lambda(N)=0$), podemos convenir que
\begin{equation*}
f\cdot\chi_E(x)=
\begin{cases}
f(x) & \text{si } x\in E\\
0 & \text{si } x\notin E
\end{cases}
\end{equation*} Diremos que $f$ es medible sobre $E$ si la función definida en c.t.p. $f\cdot\chi_E$ es medible. Definimos la integral de $f$ sobre $E$ como antes (siempre que tenga sentido).

Definición. Diremos que $f$ es integrable sobre $E$, si $f\chi_E\in L^1(\mathbb{R}^n)$, y lo denotaremos como $f\in L^1(E)$.

Ejemplos y casos particulares

Ejemplo. Como un caso particular, tenemos la integral sobre todo $\mathbb{R}^n$: $$\int_{\mathbb{R}^n} f \ \mathrm{d}\lambda=\int f\chi_{\mathbb{R}^n} \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$

$\triangle$

Ejemplo. Sea \begin{equation*}
f(x) =
\begin{cases}
\frac{x}{|x|} & \text{ si } x \neq 0 \\
0 & \text{ si } x = 0.
\end{cases} \end{equation*} Entonces $$\int_{[2,3]}f \ \mathrm{d}\lambda = \int f\chi_{[2,3]} \ \mathrm{d}\lambda=\int \chi_{[2,3]} \ \mathrm{d}\lambda=\lambda([2,3])=1;$$

\begin{align*}
\int_{(-1,1)}f \ \mathrm{d}\lambda &= \int f\chi_{(-1,1)} \ \mathrm{d}\lambda= \int (-1)\chi_{(-1,0)} \ \mathrm{d}\lambda+\int (1)\chi_{(0,1)} \ \mathrm{d}\lambda\\
&=-\lambda((-1,0))+\lambda((0,1))=0.
\end{align*}

$\triangle$

Las integrales sobre intervalos son particularmente frecuentes, así que conviene establecer notación especial para estas. Tomaremos prestada la notación usual para integrales de Riemann sobre intervalos. Esto no es al azar, como veremos más adelante, la integral de Riemann sobre un intervalo es un caso particular de la integral de Lebesgue.

Notación. Denotaremos las integrales sobre un intervalo $I\subseteq \mathbb{R}$ con extremos $a<b$, como $$\int_a^bf \ \mathrm{d}\lambda=\int_a^bf(x) \ \mathrm{d}x.$$ Observa que el tipo de intervalo (abierto, semicerrado, etc.) es irrelevante pues los extremos de un intervalo son conjuntos de medida cero.

Para ilustrar, las integrales del ejemplo anterior se reescribirían como: $$\int_2^3f \ \mathrm{d}\lambda; \ \ \ \ \ \int_{-1}^1f \ \mathrm{d}\lambda.$$ Respectivamente.

Ejemplo. La integral sobre cualquier conjunto de medida cero es cero. En efecto, si $f$ es medible sobre $E$ y $\lambda(E)=0$, tenemos que $f\chi_E=0$ en c.t.p. de $\mathbb{R}^n$ $\implies$ $\int_E f \ \mathrm{d}\lambda=\int f\chi_E \ \mathrm{d}\lambda=0$.

$\triangle$

Ejemplo. Si $f\in L^1(\mathbb{R}^n)$ $\implies$ $f\in L^1(E)$ para cualquier $E$ subconjunto medible, pues $|f\chi_E|\leq |f|$ $\implies$ $\int |f\chi_E| \ \mathrm{d}\lambda\leq \int |f| \ \mathrm{d}\lambda<\infty$.

Más generalmente, si $f\in L^1(F)$ y $E\subseteq F$ $\implies$ $f\in L^1(E)$, pues $|f\chi_E|\leq |f\chi_F|$.

El regreso es falso. Por ejemplo, la función constante $g\equiv 1$ cumple que $g\in L^1(E)$ para cualquier $E$ con medida finita pues $\int_E g \ \mathrm{d}\lambda=\int 1\chi_E \ \mathrm{d}\lambda=\lambda(E)<\infty$. Sin embargo, $g\notin L^1(\mathbb{R}^n)$, ya que $\int g \ \mathrm{d}\lambda=\infty$.

$\triangle$

Ejemplo. Cualquier función medible y acotada es integrable sobre un conjunto de medida finita: si $|f|\leq M$ sobre $E$, entonces $$\int_E |f| \ \mathrm{d}\lambda=\int |f\chi_E| \ \mathrm{d}\lambda\leq M \int \chi_E \ \mathrm{d}\lambda=M\lambda(E)<\infty.$$

$\triangle$

Propiedades de la integral sobre subconjuntos

Las siguientes propiedades son todas consecuencias sencillas de la definición y sus análogos para la integral en todo $\mathbb{R}^n$. Omitimos la demostración.

Proposición. Sean $A,B\in \mathcal{L}$ . Entonces:

1. Si $f,g\in L^1(A)$ y $a,b\in \mathbb{R}$, entonces $$\int_A af+bg \ \mathrm{d}\lambda=a\int_A f \ \mathrm{d}\lambda+b\int_A g \ \mathrm{d}\lambda.$$
2. Si $f=g$ en c.t.p. sobre $A$ y $f\in L^1(A)$ entonces $g\in L^1(A)$ con $$\int_A f \ \mathrm{d}\lambda=\int_A g \ \mathrm{d}\lambda.$$
3. Si $f\in L^1(A),L^1(B)$ y $\lambda(A\cap B)=0$ entonces $$\int_{A\cup B} f \ \mathrm{d}\lambda=\int_A f \ \mathrm{d}\lambda+\int_B f \ \mathrm{d}\lambda.$$
4. (Monotonía sobre funciones).) Si $f,g\in L^1(A)$ y $f\leq g$ entonces $$\int_A f \ \mathrm{d}\lambda \leq \int_A g \ \mathrm{d}\lambda.$$
5. (Monotonía sobre conjuntos). Si $f\in L^1(B)$ con $f\geq 0$ y $A\subseteq B$ entonces $f\in L^1(A)$ y $$\int_A f \ \mathrm{d}\lambda\leq \int_B f \ \mathrm{d}\lambda.$$
6. (Desigualdad del triángulo). $f\in L^1(A)$ $\iff$ $|f|\in L^1(A)$. Además $$ \left| \int_A f \ \mathrm{d}\lambda \right| \leq \int_A |f| \ \mathrm{d}\lambda.$$
7. (Convergencia monótona). Sea $0\leq f_1\leq f_2 \leq \dots$ una sucesión creciente de funciones medibles y no negativas sobre $A$. Entonce $\lim_{k\to \infty} f_k$ es medible con $$\lim_{k\to \infty} \int_A f_k \ \mathrm{d}\lambda=\int_A \lim f_k \ \mathrm{d}\lambda.$$
8. (Convergencia dominada). Sea $\{ f_k \}_{k=1}^{\infty} $ una sucesión de funciones medibles sobre $A$ tales que existe $g\in L^1(A)$ con: $$|f_k(x)|\leq g(x)$$ Para casi todo $x\in A$. Entonces $\lim f_k$ es integrable sobre $A$ con $$\lim_{k\to \infty} \int_A f_k \ \mathrm{d}\lambda=\int_A \lim f_k \ \mathrm{d}\lambda.$$

$\square$

Proposición (Aditividad numerable de la integral). Sean $E_1,E_2,\dots$ conjuntos medibles disjuntos y $E=\bigcup_{k=1}^{\infty}E_k$. Sea $f:E\to [-\infty,\infty]$ medible sobre $E$. Supongamos adicionalmente que ocurre alguna de las dos siguientes:

• $f\geq 0$.
• $f\in L^1(E)$.

Entonces $$\int_E f \ \mathrm{d}\lambda=\sum_{k=1}^{\infty}\int_{E_k} f \ \mathrm{d}\lambda.$$

Demostración. Para el primer caso:

\begin{align*}
\int_E f \ \mathrm{d}\lambda &= \int f\chi_E \ \mathrm{d}\lambda \\
&= \int \sum_{k=1}^{\infty} f\chi_{E_k} \ \mathrm{d}\lambda \\
&= \sum_{k=1}^{\infty} \int f\chi_{E_k} \ \mathrm{d}\lambda\\
&= \sum_{k=1}^{\infty} \int_{E_k} f \ \mathrm{d}\lambda
\end{align*}

En la segunda igualdad usamos $\chi_E=\sum_{k=1}^{\infty} \chi_{E_k}$, consecuencia de que los $E_k$ son ajenos. La tercera igualdad es debido a que la integral conmuta con sumas de funciones positivas.

Para el segundo caso, notemos que, similarmente al caso anterior: $$\sum_{k=1}^{\infty} \int |f|\chi_{E_k} \ \mathrm{d}\lambda=\int \sum_{k=1}^{\infty} |f|\chi_{E_k} \ \mathrm{d}\lambda=\int |f|\chi_{E} \ \mathrm{d}\lambda=\int_E |f| \ \mathrm{d}\lambda<\infty.$$

Lo que garantiza que podemos intercambiar sumas con integrales:

$$\sum_{k=1}^{\infty} \int_{E_k} f \ \mathrm{d}\lambda=\sum_{k=1}^{\infty} \int f\chi_{E_k} \ \mathrm{d}\lambda=\int \sum_{k=1}^{\infty} f\chi_{E_k} \ \mathrm{d}\lambda=\int_E f \ \mathrm{d}\lambda.$$
Como queríamos probar.

$\square$

Continuidad absoluta

Veamos ahora un resultado «de continuidad» para la integral de funciones en $L^1$. En cierto modo nos dice que «la integral sobre conjuntos pequeños es uniformemente pequeña», o alternativamente, que una función integrable no puede acumular su «masa» sobre conjuntos arbitrariamente pequeños.

Teorema (Continuidad absoluta respecto al dominio). Sea $f\in L^1(\mathbb{R}^n)$ y $\varepsilon>0$. Entonces existe $\delta>0$ tal que si $E\in \mathcal{L}$ es medible con $\lambda(E)<\delta$ entonces $$\left| \int_E f \ \mathrm{d}\lambda \right|<\varepsilon.$$

Demostración. Supongamos primero que $f\geq 0$. Por definición, existe una función simple $s\in S$ tal que $0\leq s \leq f$ y $$\int s \ \mathrm{d}\lambda > \int f \ \mathrm{d}\lambda-\frac{\varepsilon}{2}.$$

Como $s$ es simple, en particular es acotada (sólo toma una cantidad finita de valores), así que existe $C>0$ tal que $$s(x)\leq C \ \ \ \forall x\in \mathbb{R}^n.$$

Luego:

\begin{align*}
\int_E f \ \mathrm{d}\lambda &= \int_E s \ \mathrm{d}\lambda + \int_E (f-s) \ \mathrm{d}\lambda \\
&\leq \int_E C \ \mathrm{d}\lambda+\int_{\mathbb{R}
^n} (f-s) \ \mathrm{d}\lambda \\
&\leq \int_E C \ \mathrm{d}\lambda+\int_{\mathbb{R}
^n} f \ \mathrm{d}\lambda – \int_{\mathbb{R}
^n} s \ \mathrm{d}\lambda \\
&< C\lambda(E)+\frac{\varepsilon}{2}.
\end{align*}

Así que, si tomamos cualquier $E$ con $\lambda(E)< \frac{\varepsilon}{2C}=\delta$, se cumple lo buscado.

El caso general se sigue del caso no negativo aplicado a $|f|$ y la desigualdad del triángulo.

$\square$

Más adelante…

Veremos la relación que existe entre la integral de Riemann y la integral de Lebesgue. Veremos que la integral de Lebesgue es una generalización de la integral de Riemann. Esto nos permitirá usar todas las herramientas conocidas de la integral de Riemann (cuando apliquen) como el teorema fundamental del cálculo para evaluar integrales.

Tarea moral

• Sea $f$ una función definida (en c.t.p.) sobre $E$: $f:E\setminus N\to [-\infty,\infty]$ (con $\lambda(N)=0$). Demuestra que las siguientes son equivalentes:
  • $f$ es medible sobre $E$.
  • Para cada $t\in [-\infty, \infty]$, $f^{-1}([-\infty,t])\cap E\in \mathcal{L}$.
  • $f^{-1}(\pm\infty)\in \mathcal{L}$ y para cualquier $B\in \mathcal{B}$ conjunto de Borel, $f^{-1}(B)\cap E\in \mathcal{L}$.
  • $f$ es $\mathcal{L}_{E\setminus N}$-medible, donde $\mathcal{L}_{E\setminus N}$ denota la restricción sobre $E\setminus N$ de la $\sigma$-álgebra de conjuntos Lebesgue-medibles.
• Verifica las propiedades de las integrales sobre subconjuntos de la primera proposición.
• Sea $E$ un conjunto medible. Sea $f$ una función medible sobre $E$. Supongamos que existe $M>0$ tal que $\{x\in E \ | \ f(x)>M \}$ es nulo.
  • Prueba que si $\lambda(E)<\infty$, entonces $f\in L^1(E)$.
  • ¿Se cumple lo anterior si $\lambda(E)=\infty$?
• (teorema de Convergencia acotada). Sea $E$ un conjunto medible con $\lambda(E)<\infty$. Sea $\{ f_k \}_{k=1}^{\infty} $ una sucesión de funciones medibles sobre $E$ tales que existe $0\leq M <\infty$ con: $$|f_k(x)|\leq M$$ Para casi todo $x\in E$. Demuestra que $\lim f_k$ es integrable sobre $E$ con $$\lim_{k\to \infty} \int_E f_k \ \mathrm{d}\lambda=\int_E \lim f_k \ \mathrm{d}\lambda.$$ [SUGERENCIA: Esto es consecuencia del teorema de la convergencia dominada. ¿Qué función domina a la sucesión?].
• Sea $f\in L^1(\mathbb{R})$. Definamos $$F(x)=\int_0^x f(t) \ \mathrm{d}t.$$ Con la convención: $\int_b^a f(t) \ \mathrm{d}t=-\int_a^b f(t) \ \mathrm{d}t$ si $a<b$. Demuestra que $F$ es una función continua. ¿Es $F$ una función diferenciable?
• Sea $f\in L^1(\mathbb{R}^n)$. Demuestra que para cualquier $\varepsilon>0$, existe $R$ suficientemente grande tal que $$\left| \int_{\mathbb{R}^n\setminus B_R(0)} f \ \mathrm{d}\lambda \right|<\varepsilon.$$ Donde $B_R(0)$ denota la bola de radio $R$ con centro en el orígen.

Introducción

El concepto de «casi donde sea» (o «en casi todo punto») refiere que dos objetos matemáticos (por ejemplo funciones) pueden considerarse equivalentes si coinciden excepto en un conjunto de medida cero. En términos de integración, esto significa que cualquier propiedad definida mediante integrales permanece invariante aunque las funciones difieran en conjuntos «irrelevantes». Este concepto simplifica problemas al ignorar comportamientos excepcionales sin importancia global.

Algunos Lemas

La siguiente serie de Lemas refuerzan la idea de que, a ojos de la integral, dos objetos son «iguales» si coinciden salvo en conjuntos de medida cero.

Lema. Sea $f:\mathbb{R}^n\to[-\infty,\infty]$ una función medible. Si $g:\mathbb{R}^n\to [-\infty,\infty]$ es una función tal que $Z=\{ x \ | \ f(x)\neq g(x) \}$ es un conjunto nulo, entonces $g$ es medible.

Demostración. Para cualquier $t\in \mathbb [-\infty,\infty]$, podemos escribir:

$$g^{-1}([-\infty,t])=(f^{-1}([-\infty,t])\setminus B)\cup A.$$

Donde $$A=\{ x \ | \ g(x)\in [-\infty,t]; \ g(x)\neq f(x) \}$$ Y $$B=\{ x \ | \ f(x)\in [-\infty,t]; \ g(x)\neq f(x) \}.$$

Claramente $A,B\subseteq Z$. Luego $\lambda(A)=\lambda(B)=\lambda(Z)=0$ $\implies$ $A$ y $B$ son medibles (cualquier conjunto nulo es medible). Como $f^{-1}([-\infty,t])$, $A$ y $B$ son medibles, se sigue que $g^{-1}([-\infty,t])$ es un conjunto medible.

$\square$

Lema. Si $f:\mathbb{R}^n \to [0,\infty]$ es una función no negativa tal que $f(x)=0$ salvo un conjunto de medida cero, entonces $$\int f \ \mathrm{d}\lambda = 0.$$

Demostración. Por el lema anterior, $f$ es medible (es 0 ). Por no negatividad, $\int f \ \mathrm{d}\lambda\geq 0$.

Si $\int f \ \mathrm{d}\lambda>0$, por definición de la integral, existiría una función simple $s\in S$ tal que $s\leq f$ y $$0<\int s \ \mathrm{d}\lambda\leq \int f \ \mathrm{d}\lambda.$$ Al ser simple, podemos escribir $s=\sum_{k=1}^{m}\alpha_k\chi_{A_k}$, con $\alpha_1,\dots,\alpha_m>0$ y $A_1,\dots,A_m$ ajenos. Como $\int s \ \mathrm{d}\lambda=\sum_{k=1}^{m}\alpha_k\lambda(A_k)>0$, necesariamente existiría algún $A_r$ con $\lambda(A_r)>0$. Sin embargo, esto implica que $f\geq \alpha_r>0$ sobre $A_r$, lo que contradice que $f=0$ salvo un conjunto nulo.

Por tanto, la única posibilidad es $\int f \ \mathrm{d}\lambda=0$.

$\square$

De hecho, podemos relajar la condición $f\geq 0$ en el Lema anterior:

Corolario. Si $f:\mathbb{R}^n \to [-\infty,\infty]$ es una función tal que $f(x)=0$ salvo un conjunto de medida cero, entonces $f\in L^1(\mathbb{R}^n)$ y $$\int f \ \mathrm{d}\lambda = 0.$$

Demostración. $f$ es medible por el primer Lema. Aplicando el lema anterior a $f_+$ y $f_-$ por separado, se sigue que $\int f \ \mathrm{d}\lambda=\int f_+ \ \mathrm{d}\lambda-\int f_- \ \mathrm{d}\lambda=0-0=0.$

$\square$

Proposición (Insensibilidad de la integral).

• Sea $f:\mathbb{R}^n\to [0,\infty]$ una función medible no negativa. Si $g:\mathbb{R}^n\to [-\infty,\infty]$ es tal que el conjunto $Z=\{ x \ | \ f(x)\neq g(x) \}$ es nulo, entonces $g$ es medible y $$\int g \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$
• Sea $f:\mathbb{R}^n\to [-\infty,\infty]$ una función en $L^1(\mathbb{R}^n)$. Si $g:\mathbb{R}^n\to [-\infty,\infty]$ es tal que el conjunto $Z=\{ x \ | \ f(x)\neq g(x) \}$ es nulo, entonces $g\in L^1(\mathbb{R}^n)$ y $$\int g \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$

Demostración. Los lemas anteriores aseguran que $g$ es medible en ambos casos.

Para la primera parte, supongamos primero que $g$ es no negativa. Podemos escribir $f=f\cdot\chi_{Z^c}+f\cdot\chi_Z$ y $g=f\cdot\chi_{Z^c}+g\cdot\chi_Z$. En ambos casos, la función de la derecha es 0 salvo quizá un conjunto nulo ($Z$). Entonces:

\begin{align*}
\int f \ \mathrm{d}\lambda &= \int f\cdot\chi_{Z^c} \ \mathrm{d}\lambda+\int f\cdot\chi_Z \ \mathrm{d}\lambda \\
&= \int f\cdot\chi_{Z^c} \ \mathrm{d}\lambda+0 \\
&= \int g\cdot\chi_{Z^c} \ \mathrm{d}\lambda+0 \\
&= \int g\cdot\chi_{Z^c} \ \mathrm{d}\lambda + \int g\cdot\chi_{Z} \ \mathrm{d}\lambda \\
&= \int g \ \mathrm{d}\lambda
\end{align*}

Para el caso general, podemos escribir $g=g_+-g_-$, donde $g_+=f$ y $g_-=0$ salvo en conjuntos de medida cero. Usando el caso anterior y los lemas:

$$\int g \ \mathrm{d}\lambda=\int g_+ \ \mathrm{d}\lambda-\int g_- \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda-0=\int f \ \mathrm{d}\lambda.$$

Para la segunda parte, notemos que $g-f=0$ salvo un conjunto de medida cero. Así $(g-f)\in L^1(\mathbb{R}^n)$ con $$\int (g-f) \ \mathrm{d}\lambda=0.$$
Luego, por linealidad, $g=(g-f)+f\in L^1(\mathbb{R}^n)$ y $$\int g \ \mathrm{d}\lambda=\int (g-f) \ \mathrm{d}\lambda+\int f \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$

$\square$

El concepto de casi donde sea

Definición. Decimos que una propiedad $\mathcal{P}$ en $\mathbb{R}^n$ se satisface «casi donde sea» ó «para casi todo $x$» ó «para casi todo punto«, si el conjunto $$A=\{ x\in \mathbb{R}^n \ | \ \mathcal{P}(x) \text{ NO se satisface } \}.$$

Es nulo.

Generalmente abreviaremos la expresión «en casi todo punto» y sus equivalentes como c.t.p. En la literatura inglesa se suele denotar como a.e. (por almost everywhere).

Ejemplo. Casi todos los números reales son irracionales. El conjunto de racionales $\mathbb{Q}$ es de medida cero al ser numerable.

$\triangle$

Ejemplo. Podemos reescribir la proposición de insensibilidad de la siguiente forma: Si $f\in L^1$ y $f=g$ en c.t.p, entonces $g\in L^1$ y $$\int f \ \mathrm{d}\lambda=\int g \ \mathrm{d}\lambda.$$ Esto sugiere que, a ojos de la integral, dos funciones iguales en c.t.p. son «indistinguibles».

$\triangle$

Funciones definidas en casi todo punto

Otra situación que ocurre con frecuencia es que sólo podamos asegurar que una función esté definida en c.t.p. (el último teorema de esta sección es un ejemplo de esto). Sin embargo, como sugieren los teoremas anteriores, esto es suficiente para poder hablar de su integral. Procedamos de manera precisa:

Definición. Sea $f:X\subseteq \mathbb{R}^n \to [-\infty,\infty]$ una función definida en casi todo punto (c.t.p.) de $\mathbb{R}^n$ (i.e. $\lambda(\mathbb{R}^n \setminus N)=0$). Decimos que $f$ es medible si existe una extensión medible de $f$, es decir, $g:\mathbb{R}^n\to[-\infty, \infty]$ tal que para todo $x\in X$: $$f(x)=g(x).$$ Definimos la integral de $f$ como $$\int f \ \mathrm{d}\lambda=\int g \ \mathrm{d}\lambda.$$ (Siempre que ésta tenga sentido).

Observación. Hay que notar que si $f$ admite una extensión medible, entonces cualquier extensión de $f$ será medible (primer lema de la entrada). Además, la integral no depende de la extensión tomada (por insensibilidad). Por esta razón, típicamente tomamos la «extensión por cero», es decir, la extensión que vale cero en los puntos donde $f$ no está definida originalmente.

Por todo lo anterior, no hace daño extender nuestro concepto de función medible: cada que nos refiramos a una «función medible sobre $\mathbb{R}^n$», admitiremos la posibilidad de que sea una función definida en casi todo punto de $\mathbb{R}^n$. Es inmediato ver que las propiedades de las funciones medibles también se satisfacen para las funciones medibles definidas en casi todo punto.

Convergencia en casi todo punto

Definición. Sea $\{ f_k\}_{k=1}^{\infty}$ una sucesión de funciones definidas en casi todo punto de $\mathbb{R}^n$ (i.e. $\lambda(\mathbb{R}^n \setminus N)=0$). Decimos que $\{ f_k\}_{k=1}^{\infty}$ converge en casi todo punto a $f$, si existe un conjunto de medida cero $N$ tal que para todo $x\in \mathbb{R}^n\setminus N$ $$f_k(x) \longrightarrow f(x).$$

Observación. La convergencia puntual implica la convergencia en casi todo punto. El regreso no necesariamente es cierto (tarea moral).

Observación. El límite de funciones medibles (definidas en c.t.p.) es una función medible (definida en c.t.p.). Para ver esto, basta redefinir $f_1,f_2, \dots,f$ por $0$ sobre los puntos donde no están definidas o no hay convergencia puntual (que es un conjunto de medida cero) y observar que la nueva sucesión converge puntualmente a una función igual en casi todo punto a $f$ (que será medible al ser el límite de funciones medibles).

Observación. En general los límites en casi todo punto no son únicos. Por ejemplo, cualquier función que converge a $0$ en c.t.p. también converge a $\chi_{\mathbb{Q}}$ en c.t.p. pues $\chi_{\mathbb{Q}}=0$ en c.t.p. Lo que sí podemos asegurar es que los límites son únicos salvo conjuntos de medida cero (tarea moral).

Generalización de los Teoremas de convergencia

Podemos dar generalizaciones de los teoremas de convergencia en las que consideremos convergencia en casi todo punto. Por ejemplo, para el teorema de convergencia dominada tendríamos lo siguiente.

Proposición (Convergencia dominada versión c.t.p.) Sean $f_1,f_2,\dots$ funciones medibles definidas en c.t.p. de $\mathbb{R}^n$, tales que

$$\lim_{k\to \infty} f_k(x)$$

Existe para casi todo $x\in \mathbb{R}^n$. Supongamos además que existe una función $g\in L^1$ definida en c.t.p con $$|f_k(x)|\leq g(x)$$
Para casi todo $x\in \mathbb{R}^n$ y para todo $k\in \mathbb{N}$. Entonces $$\int \left( \lim_{k\to \infty} f_k \right) \ \mathrm{d}\lambda=\lim_{k\to \infty} \int f_k \ \mathrm{d}\lambda.$$

Demostración. Sea $Z$ el conjunto de $x$ tales que: O bien $f_k(x)$ no está definida para algún $k$; o bien $\lim f_k(x)$ no existe; o bien $|f_k|(x)>g(x)$ para algún $k$. Como podemos expresar a $Z$ como una unión numerable de conjuntos nulos, el propio $Z$ debe ser nulo.

Podemos redefinir las $f_k$ y $g$ de tal manera que valgan 0 sobre $Z$. Esto no afecta las propiedades en c.t.p. ni los valores de ninguna integral, pero nos deja con las hipótesis clásicas del teorema de la convergencia dominada. El resultado se sigue de aplicar el teorema de la convergencia dominada usual sobre estas nuevas funciones y luego apelar nuevamente a la insensibilidad de la integral.

$\square$

Podemos dar generalizaciones similares para los teoremas de convergencia monótona y el Lema de Fatou. Las demostraciones son similares. A partir de ahora no haremos distinción entre las versiones usuales y en c.t.p. de estos teoremas.

Intercambio de Sumas con Integrales

El siguiente resultado es relevante. Como adelantamos, es un ejemplo en el que sólo podemos asegurar que una función esté definida en c.t.p.

Teorema. Sean $f_1,f_2,\dots$ funciones en $L^1(\mathbb{R}^n)$, tales que $$\sum_{k=1}^{\infty}\int |f_k| \ \mathrm{d}\lambda<\infty.$$ Entonces $$\sum_{k=1}^{\infty} f_k(x)$$ Existe para casi todo $x\in \mathbb{R}^n$ y además $$\int \left( \sum_{k=1}^{\infty}f_k\right) \ \mathrm{d}\lambda=\sum_{k=1}^{\infty} \int f_k \ \mathrm{d}\lambda.$$

Demostración. Sea $g=\sum_{k=1}^{\infty}|f_k|$. Ésta es una función medible y no negativa. Como consecuencia del Teorema de la convergencia monótona tenemos:

$$\int g \ \mathrm{d}\lambda= \int \sum_{k=1}^{\infty}|f_k| \ \mathrm{d}\lambda=\sum_{k=1}^{\infty}\int |f_k| \ \mathrm{d}\lambda<\infty.$$ $$\implies g\in L^1.$$ Como $g$ es integrable, sabemos que $g<\infty$ en c.t.p. $\implies$ la serie $\sum_{k=1}^{\infty}f_k(x)$ converge absolutamente para casi todo $x\in \mathbb{R}^n$ (en particular converge para casi todo $x\in \mathbb{R}^n$). Además, es claro que para cada $N\in \mathbb{N}$: $|\sum_{k=1}^{N}f_k(x)|\leq \sum_{k=1}^{\infty}|f_k|(x)= g(x)$ para casi todo $x$. Aplicando el teorema de la convergencia dominada sobre la sucesión de sumas parciales $\sum_{k=1}^{N}f_k$ concluimos: $$\int \left( \sum_{k=1}^{\infty}f_k\right) \ \mathrm{d}\lambda=\sum_{k=1}^{\infty} \int f_k \ \mathrm{d}\lambda.$$

$\square$

Más adelante…

Definiremos la integral sobre subconjuntos de $\mathbb{R}^n$ y sus principales propiedades.

Tarea moral

• Demuestra que los límites en casi todo punto son únicos salvo conjuntos de medida cero, es decir, que si una sucesión $\{ f_k\}_{k=1}^{\infty}$ converge en c.t.p. a $f_1$ y a $f_2$, entonces $f_1=f_2$ en c.t.p.
• Sea $f_k=\chi_{[0,\frac{1}{k}]}$. ¿A que función converge puntualmente la sucesión $f_k$? ¿La sucesión converge en c.t.p. a $0$?
• Enuncia y demuestra una versión en casi todo punto del Teorema de la convergencia monótona.
• Enuncia y demuestra una versión en casi todo punto del Lema de Fatou.
• Sean $f,g:\mathbb{R}^n\to \mathbb{R}$ funciones continuas e iguales en casi todo punto. Prueba que de hecho $f=g$ sobre todo $\mathbb{R}^n$.

Introducción

Estamos en condiciones de enunciar y demostrar otro de los teoremas más importantes en la teoría de integración de Lebesgue: El teorema de la convergnecia Dominada. Éste nos garantiza condiciones «relativamente débiles» bajo las cuales podemos intercambiar límites e integrales. La gracia de este teorema es que aplica para funciones medibles de todo tipo (no necesariamente positivas o crecientes) siempre que podamos encontrar alguna función en $L^1$ que «domine» en valor absoluto a todas las demás.

Teorema de la convergencia dominada. Sea $f_1,f_2,f_3,\dots$ una sucesión de funciones medibles en $\mathbb{R}^n$ tales que : $$\lim_{k\to \infty}f_k(x)$$ Existe para todo $x\in \mathbb{R}^n$, y existe una función $g\in L^1$ tal que \begin{equation}|f_k(x)|\leq g(x) \end{equation} Para todo $x\in \mathbb{R}^n$ y $k\in \mathbb{N}$. Entonces $f\in L^1$ y $$\int \left( \lim_{k\to \infty} f_k \right) \ \mathrm{d} \lambda = \lim_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$

Demostración. Sea $$f=\lim_{k\to \infty} f_k.$$ Ésta es medible al ser el límite de funciones medibles. Más aún, por (1) se sigue que $$0\leq |f|\leq g.$$ Entonces $|f|$ (y en particular $f$) es integrable.

Observemos que la función $g+ f_k$ es medible y no negativa para todo $k$. Aplicando el Lema de Fatou:

$$\int (g+ f) \ \mathrm{d} \lambda\leq \liminf_{k\to \infty} \int (g+ f_k) \ \mathrm{d} \lambda$$
$$\implies \int g \ \mathrm{d} \lambda + \int f \ \mathrm{d} \lambda \leq \int g \ \mathrm{d} \lambda + \liminf_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$
Restando $\int g \ \mathrm{d} \lambda<\infty$ de ambos lados de la desigualdad anterior obtenemos $$ \int f \ \mathrm{d} \lambda \leq \liminf_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$

Similarmente, aplicando el Lema de Fatou a las funciones $g-f_k\geq 0$ resulta $$\int (g- f) \ \mathrm{d} \lambda\leq \liminf_{k\to \infty} \int (g- f_k) \ \mathrm{d} \lambda$$ $$\implies \int g \ \mathrm{d} \lambda – \int f \ \mathrm{d} \lambda \leq \int g \ \mathrm{d} \lambda – \limsup_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$ $$\implies \limsup_{k\to \infty} \int f_k \ \mathrm{d} \lambda \leq \int f \ \mathrm{d} \lambda.$$

(En el segundo renglón usamos que $\liminf_k -a_k=-\limsup a_k$). Combinando las desigualdades obtenidas concluimos que $$ \int f \ \mathrm{d}\lambda \leq \liminf_{k\to \infty} \int f_k \ \mathrm{d} \lambda \leq \limsup_{k\to \infty} \int f_k \ \mathrm{d} \lambda \leq \int f \ {d}\lambda. $$ Es decir, $\lim_k \int f_k \ \mathrm{d}\lambda$ existe y es igual a $$\lim_{k\to \infty} \int f_k \ \mathrm{d} \lambda=\int f \ \mathrm{d} \lambda.$$

$\square$

Algunos ejercicios resueltos

Para fijar ideas, veamos un par de ejercicios resueltos.

Ejercicio. Sea $f\in L^1(\mathbb{R}^n)$ y $A_1\subseteq A_
2\subseteq \dots$ una sucesión creciente de conjuntos medibles tales que $\mathbb{R}^n=\bigcup_{k=1}^{\infty} A_k$. Demuestra que $$\lim_{k\to \infty} \int f\cdot \chi_{A_k} \ \mathrm{d}\mu=\int f \ \mathrm{d}\mu.$$

Solución. Las funciones $f\cdot \chi_{A_k}$ son medibles al ser producto de funciones medibles. Más aún, son integrables pues $$|f\cdot\chi_{A_k}|\leq |f| \ \ \ \ \ \forall k\in \mathbb{N} .$$ Como $f\in L^1$ $\implies$ $|f|\in L^1$, así que el estimado anterior nos dice que podemos «dominar» las funciones $f\cdot \chi_{A_k}$ por la función $g=|f|\in L^1$.
Ahora, como $\bigcup_{k=1}^{\infty} A_k=\mathbb{R}^n$, para cada $x\in \mathbb{R}^n$, existe algún entero $M_x$ suficientemente grande tal que $x\in A_{k}$ para todo $k\geq M_x$. Esto nos dice que $$f(x)\cdot \chi_{A_k}(x)=f(x)\cdot 1 =f(x) \ \ \ \ \ \forall k\geq M_x.$$ Como lo anterior se satisface para cualquier $x\in \mathbb{R}^n$, concluimos que $$\lim_{k\to \infty} (f\cdot \chi_{A_k})=f.$$ Finalmente, aplicando el teorema de la convergencia dominada a la sucesión de funciones $f\cdot \chi_{A_k}$ (tomando $|f|=g\in L^1$ como la función que «domina» a la sucesión), concluimos que $$\lim_{k\to \infty} \int f\cdot \chi_{A_k} \ \mathrm{d}\mu=\int f \ \mathrm{d}\mu.$$

$\triangle$

Observación. En el lenguaje de integración sobre subconjuntos, el resultado anterior se reescribe como: $$\lim_{k\to \infty}\int_{A_k}f \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$

Ejercicio. Sea $f\in L^1(\mathbb{R}^n)$. Demuestra que $$\lim_{k\to \infty} \int f(x)e^{-\frac{|x|^2}{k}} \ \mathrm{d}x = \int f(x) \ \mathrm{d}x.$$

Solución. Consideremos la sucesión de funciones $f_k(x)=f(x)e^{-\frac{|x|^2}{k}}$.

Como $e^{-\frac{|x|^2}{k}}\leq e^0=1$, entonces $|f_k(x)|\leq |f(x)|$ para $k=1,2,\dots$. Es decir, la función $|f|\in L^1$ domina a cada una de las $f_k$. Además $$\lim_{k\to \infty} f_k(x)=f(x)\lim_{k\to \infty} e^{-\frac{|x|^2}{k}} = f(x)\cdot e^0 = f(x).$$ Para todo $x\in \mathbb{R}^n$. Aplicando el teorema de la convergencia dominada:
$$\lim_{k\to \infty} \int f(x)e^{-\frac{|x|^2}{k}} \ \mathrm{d}x= \lim_{k\to \infty} \int f_k(x) \ \mathrm{d} x=\int \left( \lim_{k\to \infty} f_k(x) \right) \ \mathrm{d}x=\int f(x) \ \mathrm{d}x.$$

$\triangle$

Veamos ahora un ejemplo un poco más sofisticado, en el que encontrar la función integrable que «domina» a la sucesión no es del todo inmediata.

Ejercicio. Calcula $$\lim_{k\to \infty} \int_{\mathbb{R}}\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right) \ \mathrm{d}x.$$

Solución. Consideremos la sucesión $f_k(x)=\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right)$. Notemos que para cada $x\in \mathbb{R}$: \begin{equation}\lim_{k\to \infty} f_k(x)=\lim_{k\to \infty}\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right)=e^{-x^2}\sin(0)=0.\end{equation}

(Recuerda que $e^{-x}=\lim_{k\to \infty}\left( 1+\frac{x}{k} \right)^{-k}$). Así que si somos capaces de encontrar una función $g\in L^1$ que domine a la sucesión $f_k$, por el teorema de la convergencia dominada tendríamos que $$\lim_{k\to \infty}\int_{\mathbb{R}}f_k(x) \ \mathrm{d}x=\int 0 \ \mathrm{d}x=0.$$

Proponemos $$g(x)=\frac{1}{1+x^2}.$$

• Veamos que $|f_k(x)|\leq \frac{1}{1+x^2}$ para todo $x\in \mathbb{R}$ y $k\in \mathbb{N}$.

Como $|\sin(x)|\leq 1$ $\forall x$, tenemos que $$|f_k(x)|=\left| \left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right) \right|\leq \left(1+ \frac{x^2}{k} \right)^{-k}.$$

Así que es suficiente probar que $\forall x\in \mathbb{R}$ y $k\in \mathbb{N}$: $$\left(1+ \frac{x^2}{k} \right)^{-k}\leq \frac{1}{1+x^2}$$ $$\iff 1+x^2\leq \left(1+ \frac{x^2}{k} \right)^{k}.$$ Ésto último es inmediato por el teorema del binomio. Los primeros términos de $\left(1+\frac{x^2}{k}\right)^k$ son $1+\binom{k}{1}\left( \frac{x^2}{k}\right)+\dots=1+x^2+\dots$

• Veamos ahora que $g(x)=\frac{1}{1+x^2}\in L^1(\mathbb{R})$.

Más adelante, cuando veamos la equivalencia entre integral de Lebesgue e integral de Riemann, seremos capaces de calcular el valor exacto de dicha integral con muy poco trabajo. Por el momento, podemos estimar la integral con una serie convergente.

Notemos que $0\leq g(x)=\frac{1}{1+x^2}\leq 1$ $\forall x\in \mathbb{R}$. Más aún, si $|x|\geq N$ $\implies$ $|g(x)|=\frac{1}{1+x^2}\leq \frac{1}{N^2}$. Esto nos garantiza que $g(x)\leq s(x)$, donde $s$ es la función «escalonada»: \begin{equation*} s(x)= \begin{cases} 1 & \text{si } x [-1,1) \\ \frac{1}{k^2} & \text{si } x \in [k,k+1),[-(k+1),k) \end{cases} \end{equation*} Invocando el teorema de la convergencia monótona para calcular $\int s \ \mathrm{d}\lambda$ concluimos:

\begin{align*}
\int g \ \mathrm{d}\lambda &\leq \int s \ \mathrm{d}\lambda \\
&= 1\cdot\lambda([-1,1))+\sum_{k=1}^{\infty}\frac{1}{k^2}\cdot\lambda([k,k+1))+\sum_{k=1}^{\infty}\frac{1}{k^2}\cdot\lambda([-(k+1),-k)) \\
&= 2+2\sum_{k=1}^{\infty}\frac{1}{k^2} \\
&< \infty.
\end{align*}

Entonces $g$ satisface las condiciones del teorema de la convergencia dominada y los cálculos en (2) son válidos. Concluimos $$\lim_{k\to \infty} \int_{\mathbb{R}}\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right) \ \mathrm{d}x=0.$$

$\triangle$

Más adelante…

Definiremos el concepto de casi donde sea, un concepto de gran utilidad en la teoría de integración. Daremos versiones más generales de los teoremas de convergencia que hemos probado hasta ahora aprovechando esta idea.

Tarea moral

• Para cada $k\in \mathbb{N}$, definamos $f_k(x)=\frac{k\sin(x)}{1+k^2x^2}$. Encuentra $$\lim_{k\to \infty}\int f_k(x) \ \mathrm{d}x.$$ [SUGERENCIA: Encuentra el límite puntual de $\{ f_k\}_{k=1}^{\infty}$. Domina la sucesión por un múltiplo de $\frac{1}{1+x^2}\in L^1(\mathbb{R})$].
• Sea $t_k=\chi_{[k,k+1]}$ para cada $k=1,2,\dots$ Verifica que $$\lim_{k\to \infty}\int t_k \ \mathrm{d}\lambda=1\neq 0=\int \left( \lim_{k\to \infty} t_k\right) \ \mathrm{d}\lambda.$$ ¿Porqué no aplica el teorema de la convergencia dominada?
• Sea $f\in L^1(\mathbb{R}^n)$. Para cada $k\in \mathbb{N}$, definamos $A_k=\{x \ : \ |f(x)|\leq k \}$ y $f_k=f\cdot \chi_{A_k}$. Demuestra que $$\lim_{k\to \infty}\int f_k \ \mathrm{d}\lambda=\int f \mathrm{d}\lambda.$$
• (Condiciones para intercambiar límites y derivadas con integrales). Sea $f:\mathbb{R}^n\times [a,b]\to [-\infty,\infty]$ ($a<b$) tal que para cada $t\in [a,b]$ la función $f_t:\mathbb{R}^n\to [-\infty, \infty]$, dada por $f_t(x)=f(x,t)$, es integrable. Sea $F(t)=\int_{\mathbb{R}^n}f_t \ \mathrm{d}\lambda=\int_{\mathbb{R}^n}f(x,t) \ \mathrm{d}x$.
  • Supón que existe $g\in L^1(\mathbb{R}^n)$ tal que $|f(x,t)|\leq g(x)$ para todo $x,t$ y que $\lim_{t\to t_0}f(x,t)=f(x,t_0)$ para todo $x\in \mathbb{R}^n$. Prueba que $$\lim_{t\to t_0}F(t)=F(t_0).$$ En particular, si $f(x,\cdot)$ es continua para cada $x$, entonces $F$ es continua sobre $[a,b]$.
  • Supón que $\frac{\partial f}{\partial t}$ existe y además podemos encontrar $g\in L^1(\mathbb{R}^n)$ tal que $\left |\frac{\partial f}{\partial t}(x,t) \right|\leq g(x)$ para todo $(x,t)$. Prueba que $F$ es diferenciable y $$F'(x)=\int \frac{\partial f}{\partial t}(x,t) \ \mathrm{d}x.$$ [SUGERENCIA: Utiliza el teorema del valor medio para acotar el cociente de diferencias $\left| \frac{f(x,t+h)-f(x,t)}{h}\right|\leq g(x)$. Aplica el teorema de la convergencia dominada haciendo tender $h\to 0$].
• (Generalización del teorema de la convergencia dominada). Sea $f_1,f_2,\dots$ una sucesión de funciones medibles definidas sobre $\mathbb{R}^n$ tales que $$\lim_{k\to \infty}f_k(x)=f(x)$$ Existe para cada $x\in \mathbb{R}^n$. Supongamos que existen funciones $g_1,g_2,\dots \in L^1(\mathbb{R}^n)$ tales que
  • $|f_k(x)|\leq g_k(x)$ para todo $x\in \mathbb{R}^n$.
  • $\lim_{k\to \infty}g_k(x)=g(x)$ para todo $x\in \mathbb{R}^n$, con $g\in L^1(\mathbb{R}^n)$.
  • $\lim_{k\to \infty}\int g_k \ \mathrm{d}\lambda=\int g \ \mathrm{d}\lambda.$
    Demuestra que $$\lim_{k\to \infty}\int f_k \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$ [SUGERENCIA: Imita la demostración del teorema de la convergencia dominada].