Introducción

Hasta ahora, nos hemos limitado a estudiar el problema de la medida e integración en $\mathbb{R}^n$, sin embargo, todo lo que hemos visto se puede generalizar de manera automática a un contexto más general.

La integración en espacios de medida es una generalización poderosa de la integral de Lebesgue, que extiende el concepto de integración a espacios más abstractos. Es fundamental en la formulación moderna de la teoría de probabilidad y tiene un sinnúmero de consecuencias dentro del análisis y sus aplicaciones. En esta entrada definiremos el concepto de espacio de medida, veremos algunos ejemplos y sus principales propiedades.

Un salto a la generalidad

Definición.Un espacio de medida $(X,\mathcal{M},\mu)$ es una terna con:

1. $X$ un conjunto no vacío.
2. $\mathcal{M}\subseteq 2^{X}$ una $\sigma$-álgebra sobre el conjunto $X$.
3. Una medida sobre $(X,\mathcal{M})$. Esto es, una función $\mu: \mathcal{M}\to [0,\infty]$ que satisface:
   • $\mu(\emptyset)=0$
   • Para cualesquiera $A_1,A_2,\dots$ conjuntos disjuntos en $\mathcal{M}$, $$\mu\left(\bigcup_{k=1}^{\infty}A_k\right)=\sum_{k=1}^{\infty}\mu(A_k).$$

Cuando la $\sigma$-álgebra sea clara del contexto, diremos simplemente que $\mu$ es una medida sobre $X$.

En ésta y en las próximas entradas, $(X,\mathcal{M},\mu)$ denotará un espacio de medida arbitrario salvo que se especifique lo contrario.

Algunos ejemplos típicos

Las medidas generales tienen propiedades «similares» a la medida de Lebesgue, aunque pueden surgir de contextos MUY distintos. Dedicaremos esta sección a ver algunos ejemplos clásicos.

Ejemplo. Por supuesto, $X=\mathbb{R}^n$, $\mathcal{M}=\mathcal{L}_n$ y $\mu=\lambda$, forman un espacio de medida.

$\triangle$

Ejemplo. La medida de Lebesgue restringida a los conjuntos de Borel, es decir, $X=\mathbb{R}^n$, $\mathcal{M}=\mathcal{B}_n$ y $\mu=\lambda_{|\mathcal{B}_n}$, forman un espacio de medida.

$\triangle$

Ejemplo. Cualquier conjunto no vacío $X$, con $\mathcal{M}=2^X$ y la función $\mu:2^X\to [0,\infty]$, con regla $\mu(\emptyset)=0$ y $\mu(A)=\infty$ si $A\neq \emptyset$, forman un espacio de medida.

$\triangle$

Ejemplo (medida de conteo). Cualquier conjunto no vacío $X$, $\mathcal{M}=2^X$ y $\mu$ la función definida por:

\begin{equation*}
\mu(A)=
\begin{cases}
\#A & \text{si } A \text{ es finito } \\
\infty & \text{si } A \text{ es infinito }
\end{cases}
\end{equation*}

Donde $\#A$ denota la cardinalidad de $A$, forman un espacio de medida. En este caso, a la medida $\mu$ se le llama la medida de conteo sobre $X$.

Veamos que $(X,\mathcal{M},\mu)$ es efectivamente un espacio de medida. Ya sabemos que $2^X$ es una $\sigma$-álgebra sobre $X$, así que basta probar que $\mu$ es una medida. Por definición, $\mu(\emptyset)=0$, así que solo falta probar que $$\mu\left(\bigcup_{k=1}^{\infty}A_k\right)=\sum_{k=1}^{\infty}\mu(A_k).$$ Para cualesquiera $A_1,A_2\dots$ conjuntos disjuntos:

• Si algunos de los $A_i$ es infinito, entonces $\bigcup_{k=1}^{\infty}A_k$ es infinito, por lo que $\mu(\bigcup_{k=1}^{\infty}A_k)=\infty$. Por otro lado, como $\mu(A_i)=\infty$, tenemos $\sum_{k=1}^{\infty}\mu(A_k)=\infty=\mu(\bigcup_{k=1}^{\infty}A_k)$.
• Si todos los $A_k$ son finitos pero $\#A_k>0$ para una cantidad infinita de $k$, entonces $\bigcup_{k=1}^{\infty}A_k$ es infinito $\implies$ $\mu(\bigcup_{k=1}^{\infty}A_k)=\infty$. De igual manera $\sum_{k=1}^{\infty}\mu(A_k)=\infty$ al tener una cantidad infinita de sumandos $\geq 1$.
• Si $\#A=0$ salvo para una cantidad finita de $k$, digamos $A_1,\dots, A_N$ $$\implies \bigcup_{k=1}^{\infty}A_k=\bigcup_{k=1}^{N}A_k$$ Finalmente, por definición y el hecho que $A_1,\dots, A_N$ son disjuntos: $$\implies \mu\left (\bigcup_{k=1}^{\infty}A_k\right)=\sum_{k=1}^{N} \#A_k=\sum_{k=1}^{N}\mu(A_k)=\sum_{k=1}^{\infty}\mu(A_k).$$

$\triangle$

Ejemplo. Sea $X$ un conjunto no vacío $X$ y $x_0\in X$ un punto arbitrario pero fijo. Definimos la función $\mu:2^X\to [0,\infty]$ como $\mu(A)=\chi_A(x_0)$. La terna $(X,2^X,\mu)$ es un espacio de medida (tarea moral). En este caso a $\mu$ se le conoce como la medida de Dirac en $x_0$ y se denota usualmente por $\delta(x_0)$.

$\triangle$

Ejemplo. Un espacio de Probabilidad es un espacio de medida $(X,\mathcal{M},\mu)$ tal que $\mu(X)=1$. En este caso a $\mu$ se le conoce como medida de Probabilidad. Generalmente se reserva la letra $\mathbb{P}$ para referirse a las medidas de probabilidad.

$\triangle$

Ejemplo. Sea $X=\mathbb{R}^n$ y $\mathcal{M}=\mathcal{L}_n$. Cualquier función medible no negativa $f:\mathbb{R}^n\to [0,\infty]$ induce una medida $\mu_f$ dada por $$\mu_f(E)=\int_E f \ \mathrm{d}\lambda.$$ Esto es consecuencia de la aditividad numerable de la integral.

$\triangle$

El siguiente ejemplo es importante pero bastante técnico, por lo que que nos limitamos a los detalles más generales.

Ejemplo. La medida de Hausdorff generaliza el concepto de longitud, área y volumen a dimensiones no enteras y espacios métricos arbitrarios. Dado un espacio métrico $(X,d)$, la medida de Hausdorff $s$-dimensional ($s\geq 0$) de un conjunto $A\subseteq X$, denotada $\mathcal{H}^s(A)$, se define como $$\mathcal{H}^s(A)=\liminf_{\delta \to 0}\left\{ \sum_{i\in I} (diam(U_i))^s \ | \ A\subseteq \bigcup_{i\in I} U_i, \ \ diam(U_i)<\delta\right\}.$$ Donde $diam(U_i)$ es el diámetro del conjunto $U_i$, e $I$ es un conjunto de índices a lo más numerable. Esta medida está definida sobre los conjuntos de Borel de $X$, denotados como $B_X$, que es la $\sigma$-álgebra generada por los conjuntos abiertos de $X$ (aunque se pude extender a una $\sigma$-álgebra más grande de conjuntos $\mathcal{H}^s$-medibles análoga a los conjuntos Lebesgue-medibles).

Cuando $X=\mathbb{R}^n$ y $s=n$, la medida de Hausdorff coincide con la medida de Lebesgue.

Esta medida proporciona información valiosa sobre la estructura fina de fractales como el conjunto de Cantor, el triángulo de Sierpiński, etc., además de ser clave en el estudio de la geometría de objetos con «singularidades»

$\triangle$

Propiedades de las medidas

Proposición. Sea $(X,M,\mu)$ un espacio de medida. Entonces

1. (Monotonía). Si $A,B\in \mathcal{M}$ y $A\subseteq B$, entonces $\mu(A)\leq \mu(B)$.
2. (Subaditividad). Si $\{ A_k \}_{k=1}^{\infty}\subseteq \mathcal{M}$, entonces $$\mu\left(\bigcup_{k=1}^{\infty}A_k\right)\leq \sum_{k=1}^{\infty}\mu(A_k).$$
3. (Continuidad por abajo). Si $A_1\subseteq A_2\subseteq \dots$ es una sucesión creciente de conjuntos $\mathcal{M}$-medibles, entonces $$\mu\left(\bigcup_{k=1}^{\infty}A_k\right)=\lim_{k\to \infty} \mu(A_k).$$
4. (Continuidad por arriba). $A_1\supseteq A_2\supseteq \dots$ es una sucesión decreciente de conjuntos $\mathcal{M}$-medibles, y $\mu(A_1)<\infty$, entonces $$\mu\left(\bigcap_{k=1}^{\infty}A_k\right)=\lim_{k\to \infty} \mu(A_k).$$

Comentario. Casi todas las definiciones y resultados que hemos establecido para la medida e integral de Lebesgue también son válidos para espacios de medida en general. La razón de esto es que las propiedades de la medida de Lebesgue en $\mathbb{R}^n$ son, por definición, las mismas que las de cualquier medida sobre un espacio abstracto $(X,\mathcal{M},\mu)$. Observa que la prueba debajo es idéntica al caso de la medida de Lebesgue en $\mathbb{R}^n$.

Demostración.

1. Si $A\subseteq B$, podemos escribir a $B$ como la unión ajena $B=A\cup(B\setminus A)$. Luego: $$\mu(B)=\mu(A)+\mu(B\setminus A)$$ $$\implies \mu(A)\leq \mu(B).$$ Pues $\mu(B\setminus A)\geq 0$. La primera igualdad tambien implica que $\mu()$
2. Sea $B_1=A_1$ y $B_k=A_k\setminus(\bigcup_{j=1}^{k-1}A_j)$ para $k>1$. Los $B_k$ son conjuntos disjuntos con $B_k\subseteq A_k$ para todo $k\in \mathbb{N}$. Observa que $\bigcup_{j=1}^{m}B_j=\bigcup_{j=1}^{m}A_j$. Luego, por definición de medida y 1.: $$\mu\left(\bigcup_{j=1}^{\infty}A_j\right)=\mu\left(\bigcup_{j=1}^{\infty}B_j\right)=\sum_{j=1}^{\infty}\mu(B_j)\leq \sum_{j=1}^{\infty}\mu(A_j).$$
3. Definiendo $A_0=\emptyset$, observa que $A_m=\bigcup_{j=1}^{m}A_j=\bigcup_{j=1}^{m}(A_j\setminus A_{j-1})$ y los conjuntos $\{ A_j\setminus A_{j-1}\}_{j=1}^{\infty}$ son ajenos. Luego: $$\mu\left(\bigcup_{j=1}^{\infty}A_j\right)=\sum_{j=1}^{\infty}\mu(A_j\setminus A_{j-1})=\lim_{k\to \infty}\sum_{j=1}^{k}\mu(A_j\setminus A_{j-1})=\lim_{k\to \infty} \mu(A_k).$$
4. Sea $F_j=A_1\setminus A_j$; entonces $F_1\subseteq F_2\subseteq \dots$ Para cada $j$ notemos que $\mu(A_1)=\mu(F_j)+\mu(A_j)$, además $\bigcup_{j=1}^{\infty}F_j=A_1\setminus (\bigcap_{j=1}^{\infty}A_j)$. Se sigue por 3. que: $$\mu(A_1)=\mu\left(\bigcap_{j=1}^{\infty}A_j\right)+\lim_{j\to \infty}\mu(F_j)=\mu\left(\bigcap_{j=1}^{\infty}A_j\right)+\lim_{j\to \infty}[\mu(A_1)-\mu(A_j)].$$ Restando $\mu(A_1)<\infty$ de ambos lados se sigue 4.

$\square$

Más adelante…

Con la integral de Lebesgue en $\mathbb{R}^n$ como modelo, definiremos la integral sobre espacios de medida en general y veremos algunos ejemplos.

Tarea moral

• Prueba que la medida de Dirac $\delta_{x_0}$ es una medida.
• Sea $(X,\mathcal{M},\mu)$ un espacio de medida. Sea $\mathcal{N}\subseteq \mathcal{M}$ una $\sigma$-álgebra y $\mu_{\mathcal{N}}$ la restricción de $\mu$ sobre $\mathcal{N}$. Demuestra que $(X,\mathcal{N},\mu_{|\mathcal{N}})$ es un espacio de medida.
• Sea $f\in L^1(\mathbb{R}^n)$ y $\mu_f(E)=\int_E f \ \mathrm{d}\lambda$ para todo $E\in \mathcal{L}_n$. ¿Es $\mu_f$ una medida?
• Sea $g(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$ ($\sigma>0$). Demuestra que $\int_{\mathbb{R}}g(x) \ \mathrm{d}x=1$. Deduce que $\mu_g$ es una medida de probabilidad. ($g$ es la función de densidad de probabilidad de una variable aleatoria normalmente distribuida con media $\mu$ y varianza $\sigma^2$). [SUGERENCIA: Usa un cambio de variable sobre la integral gaussiana].
• Sea $\mathcal{M}$ una $\sigma$-álgebra sobre $X$; $\mu_1,\mu_2, \dots, \mu_n$ medidas sobre $X$ y $a_1,a_2,\dots,a_n \in [0,\infty)$. Demuestra que $\sum_{k=1}^{n}a_k\mu_k$ es una medida sobre $X$.

Introducción

En esta entrada daremos finalmente una demostración del Teorema de Fubini.

Notación. Por simplicidad, a lo largo de nuestros desarrollos denotaremos como $\lambda$ a la medida de Lebesgue en cualquier dimensión. La dimensión en la que estemos trabajando será clara del contexto.

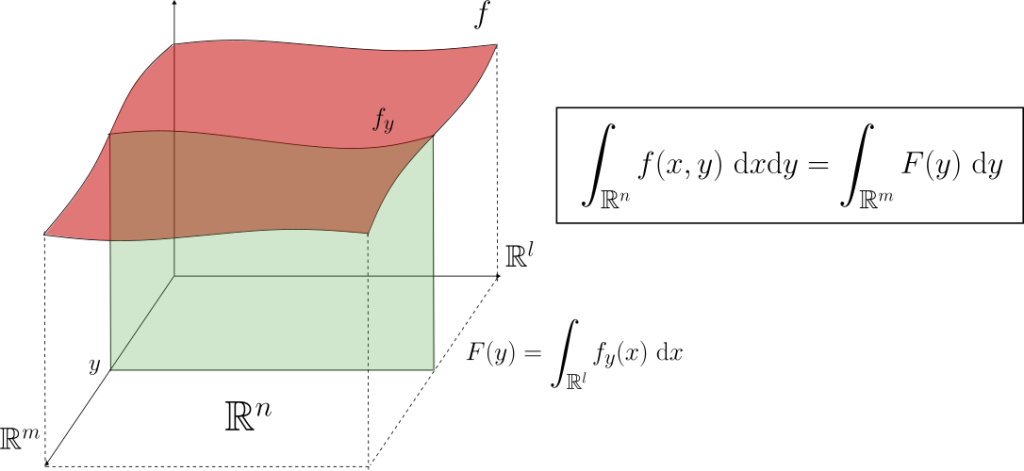
Teorema de Fubini-Tonelli (para funciones no negativas). Sea $f:\mathbb{R}^n\to[0,\infty]$ una función medible no negativa. Entonces para c.t.p. $y\in \mathbb{R}^m$, la función $$f_y:\mathbb{R}^l\to [0,\infty].$$ Es medible sobre $\mathbb{R}^l$. Más aún, la función definida en c.t.p. $$F(y)=\int_{\mathbb{R}^l}f_y(x) \ \mathrm{d}x.$$ Es medible en sobre $\mathbb{R}^m$ y $$\int_{\mathbb{R}^n}f(x,y) \ \mathrm{d}x \mathrm{d}y=\int_{\mathbb{R}^m}F(y) \ \mathrm{d}y=\int_{\mathbb{R}^m}\left( \int_{\mathbb{R}^l}f(x,y) \ \mathrm{d}x\right) \ \mathrm{d}y.$$

Demostración. La demostración se divide en varios pasos. Los dos principales son:

1. Probar primero el teorema para el caso en el que $f=\chi_A$ es la función característica de un conjunto medible y acotado $A$. Para esto, conviene primero ver los casos en que $A$ es un conjunto «sencillo» (rectángulo/abierto/compacto) y luego usar argumentos de aproximación.
2. Probar el caso general con el esquema usual: proposición para función característica $\implies$ proposición para función simple (por linealidad) $\implies$ proposición para función medible general (por convergencia monótona).

Para el primer paso, debemos probar que para cada $A\subseteq \mathbb{R}^n$ medible y acotado: $$\int_{\mathbb{R}^m}\left( \int_{\mathbb{R}^l} (\chi_A)_y(x) \ \mathrm{d}x\right) \ \mathrm{d}y=\int_{\mathbb{R}^n}\chi_A(x,y) \ \mathrm{d}x\mathrm{d}y$$ $$\iff \int_{\mathbb{R}^m}\left( \int_{\mathbb{R}^l} \chi_{A_y}(x) \ \mathrm{d}x\right) \ \mathrm{d}y=\int_{\mathbb{R}^n}\chi_A(x,y) \ \mathrm{d}x\mathrm{d}y$$ $$\iff \int_{\mathbb{R}^m}\lambda(A_y) \ \mathrm{d}y=\lambda(A).$$

• Supongamos primero que $f=\chi_J$, donde $J$ es un rectángulo semiabierto, es decir, un rectángulo de la forma $J=[a_1,b_1)\times[a_2,b_2)\times\dots\times [a_n,b_n)$.

Notemos que podemos descomponer a $J$ como un producto cartesiano de dos rectángulos semiabiertos $J=J_1\times J_2$; donde $J_1=[a_1,b_1)\times[a_2,b_2)\times\dots \times [a_l,b_l)\subseteq \mathbb{R}^l$ y $J_2=[a_{l+1},b_{l+1})\times[a_{l+2},b_{l+2})\times\dots \times [a_n,b_n)\subseteq \mathbb{R}^m$. Además, claramente $$\lambda(J)=\lambda(J_1)\lambda(J_2 ).$$

Ahora, para cualquier $y\in \mathbb{R}^m$:

\begin{equation*}
J_y=
\begin{cases}
J_1 & \text{si } y \in J_2 \\
\emptyset & \text{si } y \notin J_2
\end{cases}
\end{equation*}

Entonces:

\begin{equation*}
\lambda(J_y)=
\begin{cases}
\lambda(J_1) & \text{si } y \in J_2 \\
0 & \text{si } y \notin J_2
\end{cases}
\end{equation*}

Por lo que $$\lambda(J_y)=\lambda(J_1)\chi_{J_2}(y).$$

Es medible como función de $y$ (en $\mathbb{R}^m$) con:

\begin{align*}
\int_{\mathbb{R}^m} \lambda(J_y) \ \mathrm{d}y &= \int_{\mathbb{R}^m} \lambda(J_1)\chi_{J_2}(y) \ \mathrm{d}y \\
&= \lambda(J_1) \int_{\mathbb{R}^m} \chi_{J_2}(y) \ \mathrm{d}y \\
&= \lambda(J_1)\lambda(J_2) \\
&= \lambda(J).
\end{align*}

Lo que establece el teorema para $f=\chi_J$.

• Veamos ahora el caso en el que $f=\chi_G$, donde $G$ es un conjunto abierto.

En la entrada de invarianza de la medida de Lebesgue probamos que $G$ se puede escribir como una unión numerable de rectángulos semiabiertos ajenos: $$G=\bigcup_{k=1}^{\infty}J_k.$$
Entonces, se sigue que para cualquier $y\in \mathbb{R}^m$: $$G_y=\bigcup_{k=1}^{\infty} (J_k)_y$$ Es también una unión numerable y disjunta de rectángulos semiabiertos (algunos posiblemente vacíos). Por aditividad numerable: $$\lambda(G)=\sum_{k=1}^{\infty}\lambda(J_{k});\ \ \ \ \ \ \ \ \ \ \lambda(G_y)=\sum_{k=1}^{\infty}\lambda(J_{k,y}).$$ En particular $\lambda(G_y)$ es medible como función de $y$ (cada $\lambda(J_{k,y}) $ es medible por el caso anterior).

Finalmente, por nuestro teorema de intercambio de sumas e integrales para funciones positivas y el caso anterior:

\begin{align*}
\int_{\mathbb{R}^m}\lambda(G_y) \ \mathrm{d}y &= \int_{\mathbb{R}^m}\left( \sum_{k=1}^{\infty}\lambda(J_{k,y}) \right) \ \mathrm{d}y \\
&= \sum_{k=1}^{\infty} \left( \int_{\mathbb{R}^m}\lambda(J_{k,y}) \right) \ \mathrm{d}y \\
&= \sum_{k=1}^{\infty} \lambda(J_k) \\
&= \lambda(G).
\end{align*}

Lo que establece el teorema para $f=\chi_G$.

• Veamos ahora el caso $f=\chi_K$ con $K\subseteq \mathbb{R}^n$ compacto.

Tomemos un conjunto abierto y acotado $G$ tal que $K\subseteq G$ $\implies$ $G\setminus K$ es abierto.

Es fácil ver que para cualquier $y\in \mathbb{R}^m$, $(G\setminus K)_y=G_y\setminus K_y$ y $K_y\subseteq G_y$.

Por el caso anterior aplicado a los conjuntos abiertos $G$ y $G\setminus K$, concluimos que $\lambda(K_y)=-(\lambda(G_y)-\lambda(G_y\setminus K_y))$ es medible en $y$ y además:
$$\int_{\mathbb{R}^m}\lambda(G_y) \ \mathrm{d}y=\lambda(G).$$ Y $$\int_{\mathbb{R}^m}\lambda(G_y\setminus K_y) \ \mathrm{d}y=\lambda(G\setminus K).$$ $$\implies \int_{\mathbb{R}^m}(\lambda(G_y)-\lambda(K_y)) \ \mathrm{d}y=\lambda(G)-\lambda(K)$$ $$\implies \int_{\mathbb{R}^m}\lambda(G_y) \ \mathrm{d}y-\int_{\mathbb{R}^m}\lambda (K_y) \ \mathrm{d}y=\lambda(G)-\lambda(K).$$

Restando la última igualdad a la primera, concluimos que $$\int_{\mathbb{R}^m}\lambda (K_y) \ \mathrm{d}y=\lambda(K).$$
Como queríamos probar.

• Sea $K_1\subseteq K_2\subseteq \dots$ una sucesión creciente de conjuntos compactos en $\mathbb{R}^n$. Veamos que el resultado es válido para $B=\bigcup_{k=1}^{\infty}K_j$.

Primero notemos que para cada $y\in \mathbb{R}^m$: $$B_y=\bigcup_{k=1}^{\infty}K_{j,y}$$ Es una unión numerable y creciente de conjuntos compactos en $\mathbb{R}^l$, por lo que $B_y$ es un conjunto medible (en $\mathbb{R}^l$) y $$\lambda(K_{j,y})\uparrow \lambda(B_y).$$ En particular $\lambda(B_y)$ es medible como función de $y$ (al ser límite creciente de funciones medibles). Más aún, por el teorema de la convergencia monótona:

\begin{align*}
\int_{\mathbb{R}^m}\lambda(B_y) \ \mathrm{d}y &= \lim_{j\to \infty} \int_{\mathbb{R}^m}\lambda(K_{j,y}) \ \mathrm{d}y \\
&= \lim_{j\to \infty} \lambda(K_j) \\
&= \lambda(B).
\end{align*} Lo que completa este caso.

• Similarmente al caso anterior, sea $G_1\supseteq G_2\supseteq \dots$ una sucesión decreciente de conjuntos abiertos y acotados en $\mathbb{R}^n$. Veamos que la proposición es cierta para la intersección: $C=\bigcap_{k=1}^{\infty} G_k$.

Para ello, tomemos un compacto $K$ con $K\supseteq G_1$. Aplicando el caso anterior al conjunto $$K\setminus C=\bigcup_{j=1}^{\infty}(K\setminus G_j).$$

Se sigue que $\lambda(K_y\setminus C_y)=\lambda(K_y)-\lambda(C_y)$ es medible como función de $y$ y:
$$\int_{\mathbb{R}^m}\lambda(K_y\setminus C_y) \ \mathrm{d}y=\lambda(K\setminus C)$$ $$\implies \int_{\mathbb{R}^m}(\lambda(K_y)-\lambda(C_y) )\ \mathrm{d}y=\lambda(K\setminus C)$$ $$\implies \int_{\mathbb{R}^m}\lambda(K_y)\ \mathrm{d}y – \int_{\mathbb{R}^m}\lambda(C_y)\ \mathrm{d}y=\lambda(K)-\lambda(C).$$

Por el caso compacto, tenemos también que $\lambda(K_y)$ es medible en $y$ con: $$\int_{\mathbb{R}^m}\lambda(K_y) \ \mathrm{d}y=\lambda(K).$$ Restando las expresiones anteriores se sigue: $$\int_{\mathbb{R}^m}\lambda(C_y) \ \mathrm{d}y=\lambda(C).$$ Lo que completa este caso.

• Veamos finalmente el caso general: Sea $A\subseteq \mathbb{R}^n$ un conjunto medible y acotado arbitrario.

Por el teorema de aproximación de conjuntos medibles podemos encontrar una sucesión de conjuntos compactos $K_j$ y una sucesión de conjuntos abiertos $G_j$ tales que $$K_1\subseteq K_2 \subseteq \dots \subseteq A \subseteq \dots \subseteq G_2 \subseteq G_1.$$

Con $$\lim_{j\to \infty} \lambda(K_j)=\lambda(A)=\lim_{j\to \infty} \lambda(G_j).$$ Definamos $$B=\bigcup_{j=1}^{\infty} K_j; \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ C=\bigcap_{j=1}^{\infty}G_j.$$

Claramente $B\subseteq A\subseteq C$ y $\lambda(B)=\lambda(A)=\lambda(C)$. Por los casos anteriores: $$\int_{\mathbb{R}^m}\lambda(B_y) \ \mathrm{d}y=\lambda(B); \ \ \ \ \ \ \ \ \ \int_{\mathbb{R}^m}\lambda(C_y) \ \mathrm{d}y=\lambda(C).$$

Al restar las expresiones se sigue: $$\int_{\mathbb{R}^m}[\lambda(C_y)-\lambda(B_y)] \ \mathrm{d}y=0.$$ Como el integrando es no negativo, se sigue por propiedades de la integral que $$\lambda(C_y\setminus B_y)=\lambda(C_y)-\lambda(B_y)=0.$$ Para casi todo $y\in \mathbb{R}^m$.

Por esta razón, $C_y\setminus B_y$ es un conjunto nulo en $\mathbb{R}^l$ para c.t.p. $y\in \mathbb{R}^m$. Para tales $y$, el hecho que $B_y\subseteq A_y \subseteq C_y$ y $\lambda(B_y)=\lambda(C_y)$ implica que el propio $A_y$ es un conjunto medible de $\mathbb{R}^l$ con $\lambda(B_y)=\lambda(A_y)=\lambda(C_y)$. Como $\lambda(B_y)$ (o $\lambda(C_y)$) es medible como función sobre $y$ (por los casos anteriores) e igual en c.t.p. a $\lambda(A_y)$, se sigue que $\lambda(A_y)$ es medible como función sobre $y$. Además: \begin{align*}
\int_{\mathbb{R}^m}\lambda(A_y) \ \mathrm{d}y &= \int_{\mathbb{R}^m}\lambda(B_y) \ \mathrm{d}y \\
&= \lambda(B) \\
&= \lambda(A).
\end{align*}

Para la primera igualdad se usó que $\lambda(A_y)=\lambda(B_y)$ en c.t.p. $y\in \mathbb{R}^m$, mientras que la segunda se sigue por los casos anteriores.

Esto completa la primera parte de la demostración.

Pasemos a la segunda parte: Probar el resultado para una función medible no negativa general.

Definición. Diremos que una función simple $s\in S$, $s=\sum_{k=1}^{l} \alpha_k \chi_{A_k}$ es de soporte acotado, si cada $A_k$ es un conjunto acotado. O equivalentemente que el conjunto $\{ x \ | \ s(x)\neq 0 \}$ sea acotado. Denotaremos el conjunto de funciones simples de soporte acotado como $S_c$.

Se sigue inmediatamente de la parte anterior y linealidad que el teorema de Fubini es válido para funciones simples de soporte acotado.

Notemos que para cualquier función medible no negativa, $f:\mathbb{R}^n\to [0,\infty]$, podemos encontrar una sucesión de funciones simples y de soporte acotado $\{ r_k \}_{k=1}^{\infty}\subseteq S_c$ tales que $r_k\uparrow f$: Basta tomar cualquier sucesión de funciones simples $\{ s_k \}_{k=1}^{\infty}$ tales que $s_k\uparrow f$ y definir $r_k=s_k\cdot \chi_{[-k,k]^n}$ (¿Porqué?).

Sea entonces $f:\mathbb{R}^n\to [0,\infty]$ una función medible no negativa arbitraria y $\{ r_k \}_{k=1}^{\infty}$ una sucesión de funciones en $S_c$ tales que $$r_k\uparrow f.$$

Es claro que para cualquier $y\in \mathbb{R}^m$, $r_{k,y}\uparrow f_y$ cuando $k\to \infty$.

Ahora, como el teorema de Fubini es válido para funciones en $S_c$, tenemos:

$r_{k,y}:\mathbb{R}^l\to[0,\infty]$ es medible para c.t.p. $y\in \mathbb{R}^m$; la función $R_k(y)=\int_{\mathbb{R}^l}r_{k,y}(x) \ \mathrm{d}x$ es medible sobre $\mathbb{R}^m$ y $$\int_{\mathbb{R}^n}r_{k}(x,y) \ \mathrm{d}x\mathrm{d}y=\int_{\mathbb{R}^m}R_{k}(y) \ \mathrm{d}y.$$

Se sigue entonces que para c.t.p. $y\in \mathbb{R}^m$, $f_y$ es medible pues es el límite creciente de las funciones medibles $r_{k,y}$. Por el teorema de la convergencia monótona, para tales $y$ se cumple:

$$F(y)=\int_{\mathbb{R}^l}f_{y}(x) \ \mathrm{d}x=\lim_{k\to \infty} \int_{\mathbb{R}^l}r_{k,y}(x) \ \mathrm{d}x=\lim_{k\to \infty} R_k(y).$$

Por monotonía el límite anterior es de hecho creciente. Así que podemos escribir: $$R_k\uparrow F$$ En c.t.p. de $\mathbb{R}^l$. Luego, $F$ es medible al ser el límite creciente (en c.t.p.) de las funciones medibles $R_k$. Más aún tenemos:
$$\int_{\mathbb{R}^m}F(y) \ \mathrm{d}y=\lim_{k\to \infty} \int_{\mathbb{R}^m}R_k(y) \ \mathrm{d}y=\lim_{k\to \infty}\int_{\mathbb{R}^n}r_{k}(x,y) \ \mathrm{d}x\mathrm{d}y=\int_{\mathbb{R}^n}f(x,y) \ \mathrm{d}x\mathrm{d}y.$$

(La primera y última igualdad se siguen del teorema de la convergencia monótona en $\mathbb{R}^m$ y $\mathbb{R}^n$ respectivamente). Lo que completa la demostración del teorema de Fubini-Tonelli.

$\square$

Más adelante…

Estudiaremos una generalización poderosa de los conceptos de medida e integración, que nos permite hablar de integral sobre espacios «abstractos».

Introducción

En esta entrada veremos varios ejemplos relacionados con el teorema de Fubini.

La condición de integrabilidad es necesaria en el Teorema de Fubini

En general, no podemos relajar las hipótesis de positividad o integrabilidad en el Teorema de Fubini. Veamos un ejemplo concreto.

Ejemplo. Consideremos $Q=(0,\infty)\times(0,\infty) $. Definamos $R\subseteq Q$ como la región acotada por las rectas $y=x$ y $y=x-1$, y $S\subseteq Q$ la región acotada por las rectas $y=x-1$, $y=x-2$ como se observa en la figura. Claramente $\lambda(R),\lambda(S)=\infty$.

Sea $f=\chi_R-\chi_S$. Ésta NO es una función integrable pues $f_+=\chi_R$ $\implies$ $\int f_+ \ \mathrm{d}\lambda=\int \chi_R \ \mathrm{d}\lambda=\infty$ y de manera similar $f_-=\chi_S$ $\implies$ $\int f_- \ \mathrm{d}\lambda=\int \chi_S \ \mathrm{d}\lambda=\infty$.

Ahora, para cada $x\geq 0$ consideremos la función: $$g(x)=\int_{0}^{\infty}f(x,y) \ \mathrm{d}y.$$ Es fácil ver que:

\begin{equation*}
g(x)=
\begin{cases}
x & \text{si } 0\leq x \leq 1 \\
2-x & \text{si } 1\leq x \leq 2 \\
0 & \text{si } 2\leq x
\end{cases}
\end{equation*}

Así que $g$ es claramente medible. Además:

$$\int_0^\infty g(x) \ \mathrm{d}x=\int_0^1 x \ \mathrm{d}x+\int_1^2 (2-x) \ \mathrm{d}x=\frac{1}{2}+\frac{1}{2}=1.$$

Por otro lado, consideremos:
$$h(y)=\int_{0}^{\infty}f(x,y) \ \mathrm{d}x.$$ Es fácil ver que en $(0,\infty)$: $$h\equiv 0 \ \implies \int_0^\infty h(y) \ \mathrm{d}y =0.$$

Es decir: $$\int_0^\infty \left( \int_0^\infty f(x,y) \ \mathrm{d}y \right) \mathrm{d}x=1\neq 0=\int_0^\infty \left( \int_0^\infty f(x,y) \ \mathrm{d}x \right) \mathrm{d}y.$$
De modo que las integrales iteradas ni siquiera coinciden.

$\triangle$

Algunos ejercicios resueltos

Veamos ahora algunos ejercicios resueltos, un poco más sofisticados, en los que el teorema de Fubini juega un papel fundamental.

Ejercicio. Calcular $$\int_R 2x^2+4xy+2x+2y^2-2y \ \mathrm{d}x\mathrm{d}y.$$ Donde $R$ es el conjunto de puntos $(x,y)\in \mathbb{R}^2$ tales que $|x|+|y|\leq 1$.

Solución. La región $R$ es un rombo con vértices $(1,0),(0,1),(-1,0),(0,-1)$, que no es un producto de conjuntos, así que no podemos usar el teorema de Fubini directamente.

Conviene entonces transformar la región de integración a una región en la que sea más sencillo aplicar el teorema de Fubini. Lo más natural es hacer un cambio de variable con una rotación de $\pm \frac{\pi}{4}$, pues de esta manera $R$ se transforma en un rectángulo, aunque por simplicidad algebráica proponemos : $$u=x+y; \ \ \ \ \ v=x-y.$$ O equivalentemente \begin{equation*}\begin{pmatrix}
u \\
v
\end{pmatrix} = \begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix} \begin{pmatrix}
x \\
y
\end{pmatrix}=T\begin{pmatrix}
x\\
y
\end{pmatrix}. \end{equation*}

Geométricamente $T$ es una rotación con ángulo $-\frac{\pi}{4}$, compuesta con una reflexión y una dilatación. Mediante este cambio, $R$ se transforma en un rectángulo $R’$ con vértices $(1,1),(1,-1),(-1,-1),(-1,1)$, es decir $R’=[-1,1]\times[-1,1]$.

Como $|\det T|=2$, se sigue por el teorema de cambio de variable y el teorema de Fubini:

\begin{align*}
\int_R 2x^2+4xy+2x+2y^2-2y \ \mathrm{d}x\mathrm{d}y &= 2\int_R (x+y)^2+(x-y) \ \mathrm{d}x\mathrm{d}y \\
&= \int_{R’} u^2+v \ \mathrm{d}u\mathrm{d}v \\
&= \int_{-1}^{1} \int_{-1}^{1} u^2+v \ \mathrm{d}u\mathrm{d}v \\
&= \int_{-1}^{1} \left[\frac{u^3}{3}\right]_{u=-1}^{u=1}+(1-(-1))v \ \mathrm{d}v \\
&= \int_{-1}^1 \frac{2}{3}+2v \ \mathrm{d}v \\
&= (1-(-1))\frac{2}{3}+2\left[\frac{v^2}{2} \right]_{v=-1}^{v=1} \\
&= \frac{4}{3}.
\end{align*}

$\triangle$

Ejercicio (Integral Gaussiana). Demuestra que $$\int_{\mathbb{R}^n} e^{-|x|^2} \ \mathrm{d}x=\pi^{\frac{n}{2}}. $$

Solución. Veamos primero el caso $n=1$: $\int_{\mathbb{R}} e^{-x^2} \ \mathrm{d}x=\sqrt{\pi} $. Notemos que la función $f(x)= e^{-x^2}$ es una función par (i.e. $f(x)=f(-x)$ $\forall x\in \mathbb{R}$) y no negativa. Haciendo el cambio de variable $y=-x$, es fácil ver que $\int_{-\infty}^{0} e^{-x^2} \ \mathrm{d}x=\int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x$, de donde $\int_{-\infty}^{\infty} e^{-x^2} \ \mathrm{d}x=2\int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x$, así que basta probar que $$\int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x=\frac{\sqrt{\pi}}{2}.$$

Para esto, calculemos $$I=\int_{(0,\infty)\times(0,\infty)} xe^{-x^2(1+y^2)} \ \mathrm{d}x\mathrm{d}y.$$ De dos formas distintas usando el teorema de Fubini. Por un lado:

\begin{align*}
I &= \int_{0}^{\infty} \int_{0}^{\infty} xe^{-x^2(1+y^2)} \ \mathrm{d}x \ \mathrm{d}y \\
&= \int_{0}^{\infty} \int_{0}^{\infty} \frac{-1}{2(1+y^2)} \left( -2x(1+y^2)e^{-x^2(1+y^2)} \right) \ \mathrm{d}x \ \mathrm{d}y \\
&= \int_{0}^{\infty} \frac{-1}{2(1+y^2)} \int_{0}^{\infty} \frac{\mathrm{d}}{\mathrm{d}x} \left( e^{-x^2(1+y^2)} \right) \ \mathrm{d}x \ \mathrm{d}y \\
&= \int_{0}^{\infty} \frac{-1}{2(1+y^2)} \left( \left[ e^{-x^2(1+y^2)} \right]_{x=0}^{x=\infty} \right) \ \mathrm{d}y \\ &= \int_{0}^{\infty} \frac{-1}{2(1+y^2)} \left( 0 – 1 \right) \ \mathrm{d}y \\
&= \int_{0}^{\infty} \frac{1}{2(1+y^2)} \ \mathrm{d}y \\
&= \frac{1}{2} \int_{0}^{\infty} \frac{\mathrm{d}}{\mathrm{d}y}\left( \arctan(y) \right) \ \mathrm{d}y \\
&= \frac{1}{2} \left[ \arctan(y) \right]_{y=0}^{y=\infty} \\
&= \frac{1}{2}[\frac{\pi}{2}-0] \\
&= \frac{\pi}{4}
\end{align*}

En la segunda igualdad multiplicamos y dividimos por $-2(1+y^2)$ para poder escribir el integrando como una derivada. En las demás, hacemos uso del teorema fundamental del cálculo, convergencia monótona y tomamos límites (ya hemos hecho este argumento varias veces así que omitimos los detalles).

Por otro lado:

\begin{align*}
I &= \int_{0}^{\infty} \int_{0}^{\infty} xe^{-x^2}e^{-x^2y^2} \ \mathrm{d}y \ \mathrm{d}x \\
&= \int_{0}^{\infty} xe^{-x^2} \int_{0}^{\infty} e^{-x^2y^2} \ \mathrm{d}y \ \mathrm{d}x \\
\end{align*}

Haciendo el cambio de variable: $z=xy$ en la integral de en medio:

\begin{align*}
&= \int_{0}^{\infty} xe^{-x^2} \int_{0}^{\infty} \frac{1}{x} e^{-z^2} \ \mathrm{d}z \ \mathrm{d}x \\
&= \int_{0}^{\infty} e^{-x^2} \int_{0}^{\infty} e^{-z^2} \ \mathrm{d}z \ \mathrm{d}x \\
&= \left( \int_{0}^{\infty} e^{-z^2} \ \mathrm{d}z \right) \left( \int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x \right) \\
&= \left( \int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x \right)^2
\end{align*}

$$\implies I=\left( \int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x \right)^2=\frac{\pi}{4}$$ $$\implies \int_{0}^{\infty} e^{-x^2} \ \mathrm{d}x = \frac{\sqrt{\pi}}{2}.$$

Esto completa el caso $n=1$. Ahora, para el caso general, simplemente notemos que:

\begin{align*}
\int_{\mathbb{R}^n} e^{-|x|^2} \ \mathrm{d}x &= \int_{\mathbb{R}} \int_{\mathbb{R}} \dots \int_{\mathbb{R}} e^{-x_1^2}e^{-x_2^2}\dots e^{-x_n^2} \ \mathrm{d}x_n \dots \mathrm{d}x_2 \mathrm{d}x_1 \\
&= \int_{\mathbb{R}} e^{-x_1^2}\left( \int_{\mathbb{R}} e^{-x_2^2} \left( \dots \int_{\mathbb{R}} e^{-x_n^2} \ \mathrm{d}x_n \dots \right) \mathrm{d}x_2 \right) \mathrm{d}x_1 \\
&= \left( \int_{\mathbb{R}} e^{-x_1^2} \ \mathrm{d}x_1 \right)\left( \int_{\mathbb{R}} e^{-x_2^2} \ \mathrm{d}x_2 \right)\dots \left( \int_{\mathbb{R}} e^{-x_n^2} \ \mathrm{d}x_n \right) \\
&= \left( \int_{\mathbb{R}} e^{-y^2} \ \mathrm{d}y \right)^n \\
&= \left( \sqrt{\pi} \right)^n \\
&= \pi^{\frac{n}{2}}.
\end{align*}

$\triangle$

Ejercicio. Sean $a_1,a_2,\dots,a_n>0$. Sea $J=(0,1)\times(0,1)\times \dots \times(0,1)$. Demuestra que $$\int_J\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}} \ \mathrm{d}x<\infty \ \iff \ \sum_{i=1}^{n}\frac{1}{a_i}>1.$$

Antes de proceder, usaremos un lema sencillo, consecuencia del teorema fundamental del cálculo. Omitimos la demostración.

Lema. $\int_0^1 y^{s-1} \ \mathrm{d}y<\infty$ $\iff$ $s>0$.

Solución. Para cada $1\leq i \leq n$, consideremos $G_i= \{ x\in J \ | \ x_j^{a_j}\leq x_i^{a_i} $ para todo $ j \}$. Claramente $J=\bigcup_{i=1}^{n}G_i$. Además, para $x\in G_i$ se cumple $x_i^{a_i}\leq x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}\leq n x_i^{a_i}$. Esto nos garantiza que:
$$\int_{G_i}\frac{1}{nx_1^{a_1}} \ \mathrm{d}x\leq \int_{G_i}\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}} \ \mathrm{d}x \leq \int_J\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}} \ \mathrm{d}x.$$ Y de manera similar:
$$ \int_J\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}} \ \mathrm{d}x\leq \sum_{i=1}^{n}\int_{G_i}\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots+x_n^{a_n}} \ \mathrm{d}x\leq \sum_{i=1}^{n}\int_{G_i}\frac{1}{x_i^{a_i}} \ \mathrm{d}x.$$

Ahora, para cada $i=1,\dots,n$ podemos escribir:

$$\int_{G_i}\frac{1}{x_i^{a_i}} \ \mathrm{d}x=\int_0^1 \left( \int_0^1 \dots \int_0^1 \frac{1}{x_i^{a_i}} \chi_{G_i}(x_1\dots,x_n) \ \mathrm{d}x_1\dots \mathrm{d}x_{i-1}\mathrm{d}x_{i+1}\dots \mathrm{d}x_n \right) \mathrm{d}x_i.$$

Para $x_i\in (0,1)$ fijo, en la integral de en medio, $x_1$ varía entre $0$ y $x_i^{\frac{a_i}{a_1}}$; $x_2$ varía entre $0$ y $x_i^{\frac{a_i}{a_2}}$, etc. De manera que la integral se puede reescribir como:

$$\int_0^1 \left( \int_0^{x_i^{\frac{a_i}{a_1}}}\dots \int_0^{x_i^{\frac{a_i}{a_{i-1}}}} \int_0^{x_i^{\frac{a_i}{a_{i+1}}}}\dots \int_0^{x_i^{\frac{a_i}{a_{n}}}} \frac{1}{x_i^{a_i}} \ \mathrm{d}x_1\dots \mathrm{d}x_{i-1}\mathrm{d}x_{i+1}\dots \mathrm{d}x_n \right) \mathrm{d}x_i $$

$$=\int_0^1 \frac{1}{x_i^{a_i}} \left( \int_0^{x_i^{\frac{a_i}{a_1}}}\dots \int_0^{x_i^{\frac{a_i}{a_{i-1}}}} \int_0^{x_i^{\frac{a_i}{a_{i+1}}}}\dots \int_0^{x_i^{\frac{a_i}{a_{n}}}} 1 \ \mathrm{d}x_1\dots \mathrm{d}x_{i-1}\mathrm{d}x_{i+1}\dots \mathrm{d}x_n \right) \mathrm{d}x_i $$
$$ =\int_0^1 \frac{1}{x_i^{a_i}} \left( x_i^{\frac{a_i}{a_1}} \right) \dots \left( x_i^{\frac{a_i}{a_{i-1}}} \right)\left( x_i^{\frac{a_i}{a_{i+1}}} \right)\dots \left( x_i^{\frac{a_i}{a_n}} \right) \ \mathrm{d}x_i$$
$$ =\int_0^1 x_i^{a_i\left( \sum_{j=1}^n\frac{1}{a_j}-1 \right)-1} \ \mathrm{d}x_i.$$

Por tanto, los estimados anteriores se pueden reescribir como:

$$\frac{1}{n} \int_0^1 x_1^{a_1\left( \sum_{j=1}^n\frac{1}{a_j}-1 \right)-1} \ \mathrm{d}x_1 \leq \int_J \frac{1}{x_1^{a_1}+\dots+x_n^{a_n}} \ \mathrm{d}x\leq \sum_{i=1}^{n}\int_0^1 x_i^{a_i\left( \sum_{j=1}^n\frac{1}{a_j}-1 \right)-1} \ \mathrm{d}x_i.$$

Se sigue entonces del Lema que $\int_J \frac{1}{x_1^{a_1}+\dots+x_n^{a_n}} \ \mathrm{d}x<\infty$ $\iff$ $\sum_{j=1}^n\frac{1}{a_j}-1>0$ $\iff$ $\sum_{j=1}^n\frac{1}{a_j}>1$.

$\triangle$

Más adelante…

Daremos finalmente una prueba del Teorema de Fubini-Tonelli.

Tarea moral

• Sea $R$ la región delimitada por las rectas $x+y=0$, $x+y=2$, $2x-y=0$ y $2x-y=3$. Calcula $$\int (2x+y) \ \mathrm{d}x\mathrm{d}y .$$ [SUGERENCIA: Utiliza el cambio de variable $u=x+y$, $v=2x-y$].
• Sea $D=\{ (x,y)\in \mathbb{R}^2 \ | \ 0 \leq x \leq y \leq 1 \}.$ Calcula $$\int_D \frac{y}{x^2+y^2} \ \mathrm{d}x\mathrm{d}y.$$
• Sean $a,b>0$. Prueba que $$\int_{0}^{\infty}\frac{e^{-ax}-e^{-bx}}{x} \ \mathrm{d}x=\log \frac{b}{a}.$$ [SUGERENCIA: Calcula de dos maneras la integral de $e^{-xy}$ sobre la franja $[0,\infty]\times [a,b]$].
• (Convoluciones). La convolución de dos funciones $f,g:\mathbb{R}^n\to [-\infty,\infty]$ se define (cuando sea posible) como la función: $$(f*g)(x)=\int_{\mathbb{R}^n} f(x-y)g(y) \ \mathrm{d}y. $$
  • Prueba que si $f$ y $g$ son medibles sobre $\mathbb{R}^n$, entonces la función $f(x-y)g(y)$ es medible sobre $\mathbb{R}^{2n}$.
  • Prueba que si $f,g\in L^1(\mathbb{R}^n)$, entonces $f(x-y)g(y)$ es integrable sobre $\mathbb{R}^{2n}$.
  • Prueba que si $f$ y $g$ son integrables, entonces la convolución está definida en casi todo punto y $(f*g)\in L^1(\mathbb{R}^n)$ con $$\int |f*g| \ \mathrm{d}\lambda\leq \left( \int |f| \ \mathrm{d}\lambda \right) \left( \int |g| \ \mathrm{d}\lambda \right) .$$
  • Si $f,g,h\in L^1(\mathbb{R}^n)$, demuestra que $$f*g=g*f$$ Y $$(f*g)*h=f*(g*h).$$ En casi todo punto.
• (Continuación del último ejercicio). Usaremos la notación del último ejercicio resuelto.
  • Definamos $J’=((0,\infty)\times \dots \times (0,\infty))\setminus J$. Prueba que $$\int_{J’}\frac{1}{x_1^{a_1}+x_2^{a_2}+\dots + x_n^{a_n}}<\infty \ \ \ \iff \ \ \ \sum_{i=1}^{n}\frac{1}{a_i}<1.$$ [SUGERENCIA: Imita la solución del último ejercicio resuelto].
  • Demuestra que existen constantes $c_1,c_2>0$ (que dependen solamente de $n$ y $a>0$) tales que para todo $x=(x_1,\dots,x_n)\in \mathbb{R}^n$: $$c_1(|x_1|^a+\dots+|x_n|^a)\leq \|x\|^a\leq c_2 (|x_1|^a+\dots+ |x_n|^a).$$ (Abusando de la notación, $|x|$ denota la norma usual en $\mathbb{R}^n$ y $|x_k|$ la norma en $\mathbb{R}$). [SUGERENCIA: Por compacidad, la función $f(x)=\frac{\sum_{i=1}^{n}|x_i|^a}{|x|}$ alcanza un máximo y un mínimo sobre la esfera unitaria $S_{n-1}= \{x \ | \ |x|=1 \}$].
  • Utiliza los incisos anteriores para probar que $$\int_{B_1(0)}\frac{1}{|x|^a} \ \mathrm{d}x < \infty \ \ \ \iff \ \ \ a<n;$$ $$\int_{B_1(0)^c}\frac{1}{|x|^a} \ \mathrm{d}x < \infty \ \ \ \iff \ \ \ a>n.$$

Introducción

Anteriormente, enunciamos el Teorema de Fubini y analizamos algunas de sus consecuencias directas. En esta entrada estudiaremos cómo el teorema de Fubini nos puede ayudar a calcular integrales sobre regiones más complicadas.

Productos de conjuntos medibles

Antes de empezar, veamos un resultado bastante intuitivo pero no trivial que será útil para justificar nuestros desarrollos más adelante.

Proposición. Sean $A\subseteq \mathbb{R}^l$ y $B\subseteq \mathbb{R}^m$. Consideremos $A\times B\subseteq \mathbb{R}^l\times \mathbb{R}^m=\mathbb{R}^n$. Si $A\in \mathcal{L}_n$ y $B\in \mathcal{L}_m$, entonces $$A\times B \in \mathcal{L}_n.$$ Y además $$\lambda(A\times B)=\lambda(A)\lambda(B).$$

Demostración. El teorema es inmediato cuando $A$ y $B$ son ambos abiertos (o ambos cerrados), pues en este caso $A\times B$ es abierto (o cerrado) y en automático medible. Más aún, por Fubini:

\begin{align*}
\lambda(A\times B) &= \int_{\mathbb{R}^n}\chi_{A\times B} (x,y) \ \mathrm{d}x \mathrm{d}y \\
&= \int_{\mathbb{R}^n}\chi_A (x) \cdot \chi_B(y) \ \mathrm{d}x \mathrm{d}y \\
&= \int_{\mathbb{R}^m}\left (\int_{\mathbb{R}^l}\chi_A (x)\cdot \chi_B(y) \ \mathrm{d}x \right) \mathrm{d}y \\
&= \int_{\mathbb{R}^m} \chi_B(y) \left (\int_{\mathbb{R}^l}\chi_A (x) \ \mathrm{d}x \right) \mathrm{d}y \\
&= \left( \int_{\mathbb{R}^l}\chi_A (x) \ \mathrm{d}x \right) \left( \int_{\mathbb{R}^m} \chi_B(y) \ \mathrm{d}x\right) \\
&= \lambda(A)\lambda(B).
\end{align*}

De hecho, este último argumento es válido siempre que $A\times B\in \mathcal{L}_n$, así que sólo necesitamos probar que $A\times B$ es medible.

Más aún, basta probar el caso en el que $A$ y $B$ son medibles y de medida finita, pues cualesquiera $A’\in \mathcal{L}_l$ y $B’\in \mathcal{L}_m$ se pueden escribir como
$$A’=\bigcup_{k=1}^{\infty} A_k; \ \ \ \ \ \ \ \ \ B’=\bigcup_{k=1}^{\infty} B_k;$$ Donde los $A_k$ y $B_k$ son conjuntos medibles de medida finita (en $\mathbb{R}^l$ y $\mathbb{R}^m$ respectivamente). Y $$A’\times B’ = \bigcup_{j,k=1}^{\infty} A_k\times B_k.$$

Supongamos entonces que $A$ y $B$ son de medida finita. Por el teorema de caracterización de conjuntos medibles, podemos encontrar subconjuntos $F_1\subseteq \mathbb{R}^l$, $F_2\subseteq \mathbb{R}^m$ cerrados y $G_1\subseteq \mathbb{R}^l$, $G_2\subseteq \mathbb{R}^m$ abiertos tales que:
$$F_1\subseteq A \subseteq G_1,$$ $$F_2\subseteq B \subseteq G_2,$$
Y: $$\lambda(G_1\setminus F_1)<\varepsilon,$$ $$\lambda(G_2\setminus F_2)<\varepsilon.$$

De manera que $F_1\times F_2$ es cerrado (en $\mathbb{R}^n$) y $G_1\times G_2$ es abierto (en $\mathbb{R}^n$), con $$F_1\times F_2 \subseteq A\times B \subseteq G_1\times G_2.$$

Ahora, notemos que

\begin{align*}
(G_1\times G_2)\setminus (F_1\times F_2) &= [(G_1\setminus F_1)\times G_2]\cup [F_1\times(G_2\setminus F_2)] \\
&\subseteq [(G_1\setminus F_1)\times G_2]\cup [G_1\times (G_2\setminus F_2)].
\end{align*}

Notemos que éste último conjunto es unión de productos de abiertos. De modo que podemoes estimar:

\begin{align*}
\lambda((G_1\times G_2)\setminus (F_1\times F_2)) &\leq \lambda([(G_1\setminus F_1)\times G_2]\cup [G_1\times (G_2\setminus F_2)]) \\
&\leq \lambda([(G_1\setminus F_1)\times G_2]) + \lambda( [G_1\times (G_2\setminus F_2)]) \\
&\leq \varepsilon \lambda(G_2)+\lambda(G_1)\varepsilon \\
&\leq \varepsilon( \lambda(B)+\varepsilon )+\varepsilon(\lambda(A)+\epsilon) \\
&= \varepsilon(\lambda(A)+\lambda(B)) +2\varepsilon ^2.
\end{align*}

En resúmen, podemos encontrar $F’=F_1\times F_2$ cerrado y $G’=G_1\times G_2$ abierto tales que $$F’\subseteq A\times B \subseteq G’$$ Y $$\lambda(G’\setminus F’)$$ Sea tan pequeño como queramos. Esto garantiza que $A\times B$ es medible (teorema de caracterización de conjuntos medibles).

$\square$

Teorema de Fubini para productos de conjuntos

Con el resultado anterior en mente, es fácil establecer una versión del teorema de Fubini para productos de conjuntos.

Teorema (Fubini para productos de conjuntos). Sean $A\in \mathcal{L}_l$ y $B\in \mathcal{L}_m$ conjuntos medibles en $\mathbb{R}^l$ y $\mathbb{R}^m$ respectivamente. Sea $f:A\times B\to [-\infty,\infty]$ una función medible que satisface cualquiera de las hipótesis del teorema de Fubini ($f\geq 0$ o $f\in L^1(A\times B)$). Entonces: $$\int_{A\times B}f(x,y) \ \mathrm{d}x\mathrm{d}y=\int_B \left( \int_A f(x,y) \ \mathrm{d}x \right) \mathrm{d}y=\int_A \left( \int_B f(x,y) \ \mathrm{d}y \right) \mathrm{d}x.$$

Demostración. Por simplicidad, probaremos solamente la primera igualdad. La segunda es completamente análoga.

Por la proposición anterior, $A\times B\in \mathcal{L}_n$ es un conjunto medible, por lo que $f\chi_{A\times B}$ es una función medible. Como $f\chi_{A\times B}\geq 0$ si $f\geq 0$ o bien $|f\chi_{A\times B}|\in L^1(\mathbb{R}^n)$ si $f\in L^1(A\times B)$, concluimos que $f\chi_{A\times B}$ satisface las hipótesis del teorema de Fubini. Luego:

\begin{align*}
\int_{A\times B}f(x,y) \ \mathrm{d}x\mathrm{d}y &= \int_{\mathbb{R}^n}f(x,y)\chi_{A\times B}(x,y) \ \mathrm{d}x \mathrm{d}y \\
&= \int_{\mathbb{R}^m} \left( \int_{\mathbb{R}^l}f(x,y)\chi_A(x)\chi_B(y) \ \mathrm{d}x \right)\mathrm{d}y \\
&=\int_{\mathbb{R}^m} \chi_B(y) \left( \int_{\mathbb{R}^l}f(x,y)\chi_A(x) \ \mathrm{d}x \right)\mathrm{d}y \\
&= \int_B \left( \int_{A}f(x,y) \ \mathrm{d}x \right)\mathrm{d}y.
\end{align*}

$\square$

Integración sobre subconjuntos

El Teorema de Fubini resulta muy útil para calcular integrales sobre regiones complejas, especialmente cuando estas pueden expresarse como productos de conjuntos o están delimitadas por funciones. Veamos algunos ejemplos sencillos.

Ejercicio. Calcular $$\int_{[0,1]\times [1,2]}x-2y \ \mathrm{d}x\mathrm{d}y.$$

Solución. Antes de aplicar el teorema de Fubini, hay que asegurarnos que la función $(x,y)\to x-2y$ es $L^1([0,1]\times [1,2])$. En este caso es sencillo:

$$|x-2y|\leq |x|+2|y|\leq (1)+2(2)\leq 5 \ \ \ \ \forall (x,y)\in [0,1]\times[1,2].$$

$$\implies \int_{[0,1]\times[1,2]}|x-2y| \ \mathrm{d}x\mathrm{d}y\leq 5\int_{[0,1]\times[1,2]}1 \ \mathrm{d}x\mathrm{d}y=5\lambda([0,1]\times[1,2])=5<\infty.$$

Así, $f\in L^1([0,1]\times [1,2])$. Entonces, aplicando el teorema de Fubini (para productos de conjuntos):

\begin{align*}
\int_{[0,1]\times [1,2]} x-2y \ \mathrm{d}x\mathrm{d}y &= \int_1^2\left( \int_0^1 x-2y \ \mathrm{d}x \right) \mathrm{d}y \\ &= \int_1^2 \left( \left[ \frac{x^2}{2}\right]_{x=0}^{x=1}-2y(1-0) \right)\mathrm{d}y \\
&= \int_1^2 \left( \frac{1}{2}-2y \right)\mathrm{d}y \\
&= \frac{1}{2}(2-1)-2\left[ \frac{y^2}{2} \right]_{y=1}^{y=2} \\
&= \frac{1}{2}-2(\frac{3}{2}) \\
&= -\frac{5}{2}.
\end{align*}

$\triangle$

Ejercicio. Sea $D=\{ (x,y)\in \mathbb{R}^2 \ | \ 0\leq y \leq x \leq 2\}$. Calcular $$\int_D \frac{y}{1+x^2} \ \mathrm{d}x\mathrm{d}y.$$

Solución. $D$ es medible al ser un conjunto compacto y $f$ es medible al ser una función continua. Por lo anterior, se sigue también que $f$ es acotada sobre $D$, digamos $\sup_D |f|\leq M$. Luego $$\int_D |f| \ \mathrm{d}\lambda\leq M\cdot \lambda(D)<\infty. $$ Concluimos que $f\in L^1(D)$. Aplicando el teorema de Fubini: $$\int_D \frac{y}{1+x^2} \ \mathrm{d}x\mathrm{d}y=\int \left( \int \frac{y}{1+x^2} \cdot \chi_D(x,y) \ \mathrm{d}y \right) \mathrm{d}x. $$

Notemos que $\chi_D(x)=\chi_{[0,2]}(x)\chi_{\{0\leq y\leq x \}}(y)$, así que lo anterior se puede escribir como $$\int \left( \int \frac{y}{1+x^2} \cdot \chi_{[0,2]}(x)\chi_{\{0\leq y\leq x \}}(y) \ \mathrm{d}y \right) \mathrm{d}x=\int \chi_{[0,2]}(x) \left( \int \frac{y}{1+x^2} \cdot\chi_{\{0\leq y\leq x \}}(y) \ \mathrm{d}y \right) \mathrm{d}x$$ $$=\int_0^2\left(\int_0^x \frac{y}{1+x^2} \ \mathrm{d}y \right) \mathrm{d}x.$$

La integral interior es: $$\int_0^x \frac{y}{1+x^2} \ \mathrm{d}y=\frac{1}{1+x^2}\int_0^x y \ \mathrm{d}y=\frac{1}{1+x^2}\left[\frac{y^2}{2} \right]_{y=0}^{y=x}=\frac{x^2}{2(1+x^2)}.$$

Por lo que la integral exterior resulta: $$\int_0^2 \frac{x^2}{2(1+x^2)} \ \mathrm{d}x=\frac{1}{2}\int_0^2\left( 1-\frac{1}{1+x^2} \right) \ \mathrm{d}x=\frac{1}{2}\left[ x-\arctan (x) \right]_{x=0}^{x=2}=\frac{1}{2}(2-\arctan(2)).$$

$\triangle$

Más adelante…

Hemos enunciado el Teorema de Fubini junto con algunas de sus consecuencias.

En la siguiente entrada veremos un par de ejercicios resueltos para ver algunas aplicaciones del teorema de Fubini.

Tarea moral

• Sean $f:\mathbb{R}^l \to [-\infty,\infty]$ y $g:\mathbb{R}^m\to [-\infty,\infty]$ funciones medibles. Prueba que la función $h:\mathbb{R}^l\times \mathbb{R}^m\to [-\infty,\infty]$ dada por $h(x,y)=f(x)g(y)$ es una función medible. [SUGERENCIA: Basta probar por separado que $h_1(x,y)=f(x)$ y $h_2(x,y)= g(y)$ son funciones medibles. ¿Quién es $h_1^{-1}([-\infty,t])$ y $h_2^{-1}([-\infty,t])$?].
• Sea $E\in \mathcal{L}_n$ y $f: E \to [0,\infty]$ una función medible y no negativa sobre $E$. Considera la región bajo la gráfica de $f$: $G_f=\{(x,s)\in \mathbb{R}^{n+1} \ | \ 0\leq s \leq f(x) \}$.
  • Demuestra que $G_f$ es un conjunto medible y $$\lambda(G_f)=\int_{E}f(x) \ \mathrm{d}x.$$ [SUGERENCIA: Prueba primero el caso en el que $f=\chi_A$ es una función característica. Deduce el resultado para funciones simples y finalmente para funciones no negativas en general].
• Sea $G_f$ como en el ejercicio anterior. Si $g:G_f \to [-\infty, \infty]$ es $\geq 0$ ó $L^1$, demuestra que $$\int_{G_f} g \ \mathrm{d}\lambda = \int_E \left( \int_0^{f(x)}g(x,s) \ \mathrm{d}s \right) \mathrm{d}x.$$
• Sea $A= \{(x,y)\in [0,1]\times [0,1] \ | \ x\leq y^2 \}$. Calcula $\lambda(A)$.
• Sea $A$ como en el ejercicio anterior. Calcula $$\int_A (x^2+y) \ \mathrm{d}x\mathrm{d}y.$$
• Sea $f(x,y)=\frac{x^2-y^2}{(x^2+y^2)^2}$ sobre $(0,1)\times (0,1)$. Verifica que $$\int_0^1\left( \int_0^1 f(x,y) \ \mathrm{d}x \right) \mathrm{d}y\neq \int_0^1\left( \int_0^1 f(x,y) \ \mathrm{d}y \right) \mathrm{d}x .$$ ¿Porqué esto no contradice el teorema de Fubini?

Introducción

El Teorema de Fubini es una herramienta fundamental en la teoría de integración, ya que permite descomponer integrales múltiples en integrales iteradas más simples. Este resultado no solo facilita los cálculos, sino que también tiene implicaciones teóricas de gran relevancia. En esta sección, estudiaremos su enunciado y algunas consecuencias, proporcionando una base sólida para resolver problemas más avanzados.

Notación

Antes de comenzar, conviene establecer algo de notación para simplificar los desarrollos más adelante.

En ésta y en las próximas entradas, $l,m,n\in \mathbb{N}$ denotarán enteros con $n=l+m$. Podemos expresar el producto cartesiano $$\mathbb{R}^n=\mathbb{R}^l\times \mathbb{R}^m.$$

Denotaremos a los puntos en $\mathbb{R}^n$ como $$z=(x,y)\in \mathbb{R}^l\times\mathbb{R}^m=\mathbb{R}^n,$$ donde $x\in \mathbb{R}^l$ y $y\in \mathbb{R}^m$.

Si $f$ es una función sobre $\mathbb{R}^n=\mathbb{R}^l\times\mathbb{R}^m$ y $y\in \mathbb{R}^m$, definimos la $y$-sección de $f$ sobre $\mathbb{R}^l$, $f_y:\mathbb{R}^l\to [-\infty,\infty]$ como: $$f_y(x)=f(x,y) \ \ \ \forall x\in \mathbb{R}^l.$$

Dado $A\subseteq \mathbb{R}^n$, y $y\in \mathbb{R}^m$, definimos la $y$-sección de $A$ como $$A_y=\{ x\in \mathbb{R}^l \ | \ (x,y)\in A \}\subseteq \mathbb{R}^l.$$

Para el caso de una función característica $\chi_A$, con $A\subseteq \mathbb{R}^n$, notemos que

\begin{equation*}
(\chi_A)_y(x)=
\begin{cases}
1 & \text{si } (x,y) \in A\\
0 & \text{si } (x,y) \in A^c
\end{cases}
\end{equation*}

O equivalentemente, $$(\chi_A)_y=\chi_{A_y}.$$

Dado $x\in \mathbb{R}^l$, definimos análogamente las $x$ secciones $f_x$ y $A_x$.

Motivación

Consideremos una función integrable $f:\mathbb{R}^n\to [-\infty,\infty]$. Como $f$ es medible, es natural pensar que $f_y:\mathbb{R}^l\to [-\infty,\infty]$ «herede cierta regularidad». Supongamos momentáneamente que $f_y$ es integrable para cada $y$ y definamos $$F(y)=\int_{\mathbb{R}^l} f_y(x) \ \mathrm{d}x.$$ Por la misma razón, es esperable pensar que $F$ sea una función integrable.

Intuitivamente, $F(y)$ representa la «masa acumulada» de $f$ en la sección $\mathbb{R}^l\times{ y }$, de modo que la «masa total» de $f$ (i.e. $\int_{\mathbb{R}^n}f(z) \ \mathrm{d}z$) debería ser la «suma» de las contribuciones sobre cada sección. Interpretando a la integral como una «versión continua de la suma», es esperable que:

$$\int_{\mathbb{R}^n}f(z) \ \mathrm{d}z=\int_{\mathbb{R}^m}F(y) \ \mathrm{d}y=\int_{\mathbb{R}^m}\int_{\mathbb{R}^l} f_y(x) \ \mathrm{d}x \ \mathrm{d}y .$$

Esto es precisamente lo que establece el teorema de Fubini.

Por desgracia, es fácil construir ejemplos de funciones medibles $f$, en los que $f_y$ no sea medible para todo $y$.

Ejemplo. Sea $E\subseteq \mathbb{R}^l$ cualquier conjunto no medible y $y_0\in \mathbb{R}^m$ un punto arbitrario. Consideremos $A=E\times{ y_0}\subseteq \mathbb{R}^{l+m}$ y su respectiva función característica $\chi_A$.

Al estar contenido en algún hiperplano, $A$ es un conjunto de medida cero y en automático es medible. En particular $\chi_A$ es una función medible. A pesar de esto, $$f_{y_0}=\chi_{A_{y_0}}=\chi_E.$$ NO es medible sobre $\mathbb{\mathbb{R}}^l$.

$\triangle$

El ejemplo anterior muestra que hay que tener cuidado con la regularidad de las secciones. Afortunadamente, el concepto de casi donde sea nos da una alternativa para resolver este problema como veremos a continuación.

El Teorema de Fubini

Notación. Para enfatizar el hecho de que las integrales debajo son «iteradas», a la integral de una función $f:\mathbb{R}^n=\mathbb{R}^l\times\mathbb{R}^m\to [-\infty,\infty]$, la denotaremos también por $$\int_{\mathbb{R}^n}f(x,y) \ \mathrm{d}x\mathrm{d}y:=\int_{\mathbb{R}^n}f(z) \ \mathrm{d}z.$$ Es decir, solamente reemplazamos $z$ por $(x,y)$ y $\mathrm{d}z$ por $\mathrm{d}x \mathrm{d}y$.

Teorema (Fubini-Tonelli para funciones no negativas). Sea $f:\mathbb{R}^n\to[0,\infty]$ una función medible no negativa. Entonces para c.t.p. $y\in \mathbb{R}^m$, la función $$f_y:\mathbb{R}^l\to [0,\infty]$$ Es medible sobre $\mathbb{R}^l$. Más aún, la función definida en c.t.p. $$F(y)=\int_{\mathbb{R}^l}f_y(x) \ \mathrm{d}x$$ Es medible sobre $\mathbb{R}^m$ y $$\int_{\mathbb{R}^n}f(x,y) \ \mathrm{d}x \mathrm{d}y=\int_{\mathbb{R}^m}F(y) \ \mathrm{d}y=\int_{\mathbb{R}^m}\left( \int_{\mathbb{R}^l}f(x,y) \ \mathrm{d}x\right) \ \mathrm{d}y.$$

La demostración requiere varios pasos, así que la posponemos para futuras entradas. De momento, daremos por hecho el resultado.

Veamos primero un ejemplo sencillo para ver como el teorema de Fubini simplifica en gran medida el cálculo de integrales.

Ejercicio. Calcular la integral $$\int_{(0,\infty)\times(0,\infty)} e^{-(x+y)} \ \mathrm{d}x\mathrm{d}y.$$

Solución. Por definición, queremos calcular, $$\int_{\mathbb{R}^2} e^{-(x+y)}\cdot \chi_{(0,\infty)^2}(x,y) \ \mathrm{d}x\mathrm{d}y.$$
Notemos que podemos escribir $e^{-(x+y)}\cdot \chi_{(0,\infty)^2}(x,y)=e^{-x}\chi_{(0,\infty)}(x)\cdot e^{-y}\chi_{(0,\infty)}(y)$. Ésta es una función medible y no negativa, así que podemos aplicar el teorema de Fubini:

$$\int_{(0,\infty)^2}e^{-(x+y)} \ \mathrm{d}x\mathrm{d}y=\int_{\mathbb{R}}\left( \int_{\mathbb{R}} e^{-x}\chi_{(0,\infty)}(x)\cdot e^{-y}\chi_{(0,\infty)}(y) \ \mathrm{d}x \right) \mathrm{d}y$$

Ahora, en la integral de en medio, el factor $$e^{-y}\chi_{(0,\infty)}(y)$$ NO depende del integrando $x$, así que lo podemos tomar como una constante y «sacarlo de la integral» por linealidad:

$$=\int_{\mathbb{R}} e^{-y}\chi_{(0,\infty)}(y) \left( \int_{\mathbb{R}} e^{-x}\chi_{(0,\infty)}(x) \ \mathrm{d}x \right) \mathrm{d}y$$

$$=\int_{\mathbb{R}} e^{-y}\chi_{(0,\infty)}(y) \left( \int_0^{\infty} e^{-x} \ \mathrm{d}x \right) \mathrm{d}y$$
Ahora el factor $\left( \int_0^{\infty} e^{-x} \ \mathrm{d}x \right)$ NO depende de $y$, por lo que podemos «sacarlo» de la integral por linealidad:

$$=\left( \int_0^{\infty} e^{-x} \ \mathrm{d}x \right)\left( \int_{\mathbb{R}} e^{-y}\chi_{(0,\infty)}(y) \ \mathrm{d}y \right)$$
$$=\left( \int_0^{\infty} e^{-x} \ \mathrm{d}x \right)\left( \int_0^{\infty} e^{-y} \ \mathrm{d}y \right)$$ $$=\left( \int_0^{\infty} e^{-x} \ \mathrm{d}x \right)^2$$

Abreviando el argumento que ya hemos hecho con el teorema fundamental del cálculo y el teorema de la convergencia monótona : $ \int_0^{\infty} e^{-x} \ \mathrm{d}x =\int_0^{\infty} (-e^{-x})’ \ \mathrm{d}x=[-e^{-x}]_{x=0}^{x=\infty}=1$, por lo que: $$\int_{(0,\infty)^2}e^{-(x+y)} \ \mathrm{d}x\mathrm{d}y=1^2=1.$$

$\triangle$

Teorema de Fubini para funciones $L^1$

El teorema de Fubini se puede generalizar fácilmente para funciones en $L^1$.

Teorema (Fubini para funciones $L^1(\mathbb{R}^n)$). Sea $f\in L^1(\mathbb{R}^n)$, Entonces

1. $f_y\in L^1(\mathbb{R}^l)$ para c.t.p. $y\in \mathbb{R}^l$. En particular $$F(y)=\int_{\mathbb{R}^l}f_y(x) \ \mathrm{d}x$$ Existe para casi todo $y\in \mathbb{R}^m$.
2. $F\in L^1(\mathbb{R}^m)$ y $$\int_{\mathbb{R}^m}F(y) \ \mathrm{d}y=\int_{\mathbb{R}^n}f(x,y) \ \mathrm{d}x\mathrm{d}y.$$

Demostración. Escribamos $f=f_+-f_-$.

Por Fubini-Tonelli se sigue que $f_{\pm,y}$ son funciones medibles en $\mathbb{R}^l$ para casi todo $y\in \mathbb{R}^m$.

$$\implies H(y):=\int_{\mathbb{R}^l}f_{+,y}(x) \ \mathrm{d}x; \ \ \ \ \ \ \ \ \ \ \ G(y):=\int_{\mathbb{R}^l}f_{-,y}(x) \ \mathrm{d}x$$ Existen en c.t.p. $y\in \mathbb{R}^m$. Además de que $$\int_{\mathbb{R}^m}H(y) \ \mathrm{d}y=\int_{\mathbb{R}^n}f_{+}(x,y) \ \mathrm{d}x\mathrm{d}y<\infty$$
Y $$\int_{\mathbb{R}^l}G(y) \ \mathrm{d}y=\int_{\mathbb{R}^n}f_{-}(x,y) \ \mathrm{d}x\mathrm{d}y<\infty.$$

Como las integrales son finitas, se sigue que $H$ y $G$ son finitas para casi todo $y\in \mathbb{R}^m$ (resultado previo). Es decir

$$\int_{\mathbb{R}^l}f_{+,y}(x) \ \mathrm{d}x<\infty;$$ $$\int_{\mathbb{R}^l}f_{-,y}(x) \ \mathrm{d}x<\infty.$$ En c.t.p. $y\in \mathbb{R}^m$. O equivalentemente, que $f_y=f_{+,y}-f_{-,y}\in L^1(\mathbb{R}^l)$ en c.t.p. $y\in \mathbb{R}^m$. Ahora, para tales $y$ tenemos:

\begin{align*}
F(y) &= \int_{\mathbb{R}^l}f_{y}(x) \ \mathrm{d}x \\
&= \int_{\mathbb{R}^l}f_{+,y}(x) \ \mathrm{d}x-\int_{\mathbb{R}^l}f_{-,y}(x) \ \mathrm{d}x \\
&= H(y)-G(x)
\end{align*}

$$\therefore F\in L^1(\mathbb{R}^m)$$ Pues $F$ es igual en c.t.p. a la función $H-G\in L^1(\mathbb{R}^m)$. Además

\begin{align*}
\int_{\mathbb{R}^m}F(y) \ \mathrm{d}y &= \int_{\mathbb{R}^m}H(y) \ \mathrm{d}y-\int_{\mathbb{R}^m}G(y) \ \mathrm{d}y \\
&= \int_{\mathbb{R}^n}f_+(x,y) \ \mathrm{d}x\mathrm{d}y- \int_{\mathbb{R}^n}f_-(x,y) \ \mathrm{d}x\mathrm{d}y \\
&= \int_{\mathbb{R}^n}f(x,y) \ \mathrm{d}x\mathrm{d}y.
\end{align*}

Que es precisamente lo que queríamos probar.

$\square$

Corolario. Supongamos que $f:\mathbb{R}^n\to[-\infty,\infty]$ satisface las hipótesis del Teorema de Fubini (ya sea $f\geq 0$ ó $f\in L^1$). Entonces $$\int_{\mathbb{R}^n}f(x,y) \ \mathrm{d}x\mathrm{d}y=\int_{\mathbb{R}^m}\left( \int_{\mathbb{R}^l}f(x,y) \ \mathrm{d}x \right) \mathrm{d}y=\int_{\mathbb{R}^l}\left( \int_{\mathbb{R}^m}f(x,y) \ \mathrm{d}y \right) \mathrm{d}x.$$

Demostración. La primera igualdad es por supuesto el teorema de Fubini. La segunda igualdad no es más que el resultado de combinar el teorema de Fubini con el cambio de variable
$$(x_1,x_2,\dots,x_l,x_{l+1},\dots,x_n)\to(x_{l+1},\dots,x_n,x_1,x_2,\dots,x_l).$$

$\square$

Integrales iteradas

Mediante varias iteraciones del teorema de Fubini, una integral puede ser descompuesta en integrales iteradas de muchas formas. Por ejemplo, podemos descomponer

\begin{align*}
\int_{\mathbb{R}^n}f(z) \ \mathrm{d}z &= \int_{\mathbb{R}^{n-1}}\left(\int_{\mathbb{R}}f(x,y) \ \mathrm{d}x_1 \right)\mathrm{d}y \\
&= \int_{\mathbb{R}^{n-2}}\left( \int_{\mathbb{R}}\left(\int_{\mathbb{R}}f(x_1,x_2,y’) \ \mathrm{d}x_1 \right) \mathrm{d}x_2 \right) \mathrm{d}y’ \\
&= \dots \\
&= \int_{\mathbb{R}}\left( \int_{\mathbb{R}}\left( \dots \int_{\mathbb{R}} f(x_1,\dots,x_{n-1},x_n)
\ \mathrm{d}x_1 \right)\dots \mathrm{d}x_{n-1} \right) \mathrm{d}x_n
\end{align*}

De igual manera

\begin{align*}
\int_{\mathbb{R}^n}f(z) \ \mathrm{d}z &= \int_{\mathbb{R}}\left(\int_{\mathbb{R}^{n-1}}f(x_1,y) \ \mathrm{d}y \right)\mathrm{d}x_1 \\
&= \int_{\mathbb{R}^m}\left( \int_{\mathbb{R}^l}f(x,y) \ \mathrm{d}x \right) \mathrm{d}y \\
&= \int_{\mathbb{R}}\left( \dots \left( \int_{\mathbb{R}} f(x_1,\dots,x_n)
\ \mathrm{d}x_{\sigma(1)} \right)\dots \right) \mathrm{d}x_{\sigma(n)}
\end{align*}

Son todas descomposiciones válidas. (En este caso $\sigma$ representa una permutación cualquiera de coordenadas).

En general tenemos mucha libertad para descomponer una integral. A la hora de resolver algún problema, es conveniente buscar la descomposición que «nos brinde mayor información» o «mejor se adapte al contexto del problema».

Hasta ahora hemos estado haciendo un gran uso de los paréntesis dentro de las integrales, principalmente para enfatizar el hecho de que las integrales son iteradas. Esto no es del todo necesario y a partir de ahora trataremos de omitirlos para aligerar la notación.

Fubini ayuda a checar integrabilidad

Algo que ocurre con frecuencia es que nos interesa calcular la integral de alguna función $f$ que sólo sabemos que es medible, pero no es $\geq 0$ y no sabemos si pertenece a $L^1$. Es decir, a priori no podemos aplicar el teorema de Fubini.

La manera usual de proceder en estos casos es aplicar el teorema de Fubini a la función $|f|$ (que es no negativa). Con suerte seremos capaces de calcular o estimar: $$\int_{\mathbb{R}
^n}|f(z)| \ \mathrm{d}z=\int_{\mathbb{R}
^m}\int_{\mathbb{R}
^l} |f(x,y)| \ \mathrm{d}x\mathrm{d}y.$$
Para así asegurarnos de que $f\in L^1$ y poder usar Fubini sobre $f$.

Más adelante…

Veremos como el teorema de Fubini se especializa a productos de conjuntos, junto con algunas consecuencias.

Tarea moral

• Calcula $$\int_{\mathbb{R}^2}\frac{1}{(x^2+1)(y^2+1)} \ \mathrm{d}x\mathrm{d}y.$$
• Calcula $$\int_{[0,1]\times [0,\infty)}x e^{-x^2y} \ \mathrm{d}x\mathrm{d}y.$$
• Calcula $$\int_{\mathbb{R}^n} e^{-(x_1+x_2+\dots+x_n)}\mathrm{d}x_1\mathrm{d}x_2\dots \mathrm{d}x_n.$$
• Sean $f:\mathbb{R}^l\to [0,\infty]$ y $g: \mathbb{R}^m\to [0,\infty]$. Supón que la función $h:\mathbb{R}^n\to [0,\infty]$ dada por $h(x,y)=f(x)g(y)$ es medible (de hecho, esto siempre es cierto y es un ejercicio de la siguiente entrada). Demuestra que $$\int_{\mathbb{R}^n}h(x,y) \ \mathrm{d}x\mathrm{d}y=\left( \int_{\mathbb{R}^l} f(x) \ \mathrm{d}x \right) \left( \int_{\mathbb{R}^m} g(y) \ \mathrm{d}y \right).$$ Prueba que lo anterior también es válido si $f\in L^1(\mathbb{R}^l)$ y $g\in L^1(\mathbb{R}^m)$. [SUGERENCIA: Para la segunda parte, aplica primero el teorema de Fubini-Tonelli sobre $|f|$ y $|g|$ para asegurarte de que $h \in L^1(\mathbb{R}^n)$ y poder usar el teorema de Fubini sobre $h$].
• Sea $f:\mathbb{R}^n\to [0,\infty)$ una función no negativa. Supón que la región bajo la gráfica de $f$, $G_f=\{(x,s)\in \mathbb{R}^n\times \mathbb{R} \ | \ 0\leq s \leq f(x)\}$, es un subconjunto medible de $\mathbb{R}^{n+1}$. Sea $g:\mathbb{R}^{n+1}\to [-\infty,\infty]$ una función medible que satisface las hipótesis del teorema de Fubini ($g\geq 0$ ó $g\in L^1(\mathbb{R}^{n+1})$). Demuestra que es posible escribir: $$\int_{G_{f}} g \ \mathrm{d}\lambda=\int_{\mathbb{R}^n}\int_0^{f(x)}g(x,s) \ \mathrm{d}s \mathrm{d}x.$$